网络舆情威胁预警等级多指标直觉模糊综合评价模型

俞裕兰，杨靛青，郭黛翎

(1.福建商学院，福建 福州 350002；2.福州大学 经济与管理学院，福建 福州 350002)

网络舆情是以网民为主体的群体，以互联网这个平台，在一定的时间、空间范围内，针对某一社会现象、事件和问题的出现、发展和变化所表达和传播的具有一定强度和影响力的各种不同的信念、情绪、态度、意见和要求的总和及其表现。随着大数据时代的到来，互联网迅猛发展，网络舆情给社会带来的影响程度不可小觑。为了避免负面的网络舆情引导公众走入歧途，甚至威胁到社会的稳定发展，设计有效的网络舆情威胁预警等级评价模型，及时进行预警并采取有效的应对策略变得十分重要。

近年来，不少学者对网络舆情威胁预警评价指标进行了研究。Cho等[1]研究提出了意见领袖的言论能够加速舆情扩散的观点。戴媛等[2]提出了三级指标体系评判网络舆情的安全程度；王青等[3]对舆情系统进行E-R分析，从内容强度、传播热度、舆情生长规律和受众倾向度4个方面归纳整理出网络舆情监测指标；兰月新[4]考虑了“网民反应”、“舆情信息特征”、“事态扩散情况”在安全评估中的作用，构建了突发事件评估指标体系；贺恩锋等[5]选取广度、强度、效度、倾向性、相关度5方面的影响力因子来量化舆情；冯江平等[6]综合考虑多学科、多主体交叉产生的影响，多角度构建网络舆情评价指标体系；相关文献对网络舆情威胁预警评价指标进行了详细地分析，但是，缺乏较为全面的综合性的多层级的预警评价指标。

为了对预警等级进行更清晰的分类，学者们构建了相关评价模型进行网络舆情态势的威胁预警等级评价研究。武慧娟等[7]从网络舆情的生命周期入手，利用熵权法确定指标权重，构建综合评价模型得到预警等级；张艳丰等[8]通过扎根理论建立了指标体系，运用模糊AHP法确定对应权重，使用直觉模糊推理算法构建模型对网络舆情进行了评价；孙玲芳等[9]依据可变模糊集理论构建了舆情指标预警模型，使用级别特征值代替最大隶属度原则进行等级定量评价；张芳等[10]则选择指派方法建立隶属函数，得到隶属度矩阵，通过模糊综合评价模型得到网络舆情威胁预警等级；王铁套等[11]通过模糊综合评价方法将指标数值化，使用经过改进的Elman神经网络模型综合评判模型并得到网络舆情威胁等级；陈培友等[12]聚焦社交网络舆情，构建包含多主体影响因子的指标体系，综合运用灰色模糊评价法和网络层次分析法构建基于ANP-灰色模糊的风险预警模型，根据模型综合评价结果判定所对应的风险预警等级。相关文献的研究主要使用传统模糊综合评价模型中的限行加权平均法，本文将考虑到相对贴近程度以及各指标对于各威胁等级的隶属度与最大、最小隶属度的偏离程度，用基于直觉模糊相似度的TOPSIS法确定定性指标的等级隶属度，进而选用模糊优选法代替传统模糊综合评价模型中的限行加权平均法，从而得到各威胁等级更加准确的隶属度的多指标直觉模糊综合评价模型。

1 网络舆情威胁预警等级评价指标分析与体系构建

本文从主体要素、客体要素、外部要素三方面出发，构建如图1的三层次综合评价指标体系。为便于表述，将一级、二级、三级威胁等级评价指标分别表示为 xi（i=1,2，…，n）、xij（j=1,2，…，ni）、xijl（l=1,2，…，nij）。

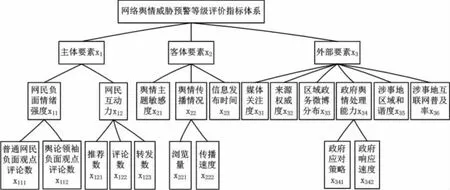
图1 网络舆情威胁预警等级评价指标体系

2 网络舆情威胁预警等级综合评价模型

据国际、国内相关部门规定，本文将网络舆情威胁等级划分为红色预警（Ⅰ级特重警情）、橙色预警（Ⅱ级重度警情）、黄色预警（Ⅲ级中度警情）和蓝色预警（Ⅳ级轻度警情）。

2.1 网络舆情威胁预警等级隶属度的确定

2.1.1 基于等级隶属函数确定定量指标等级隶属度

本文选用正态型隶属函数（如表1）来确定定量指标等级隶属度，并确定等级隶属函数的参数和划分界限。其中A(x)表示等级隶属函数，x表示指标值，c和m为常数。

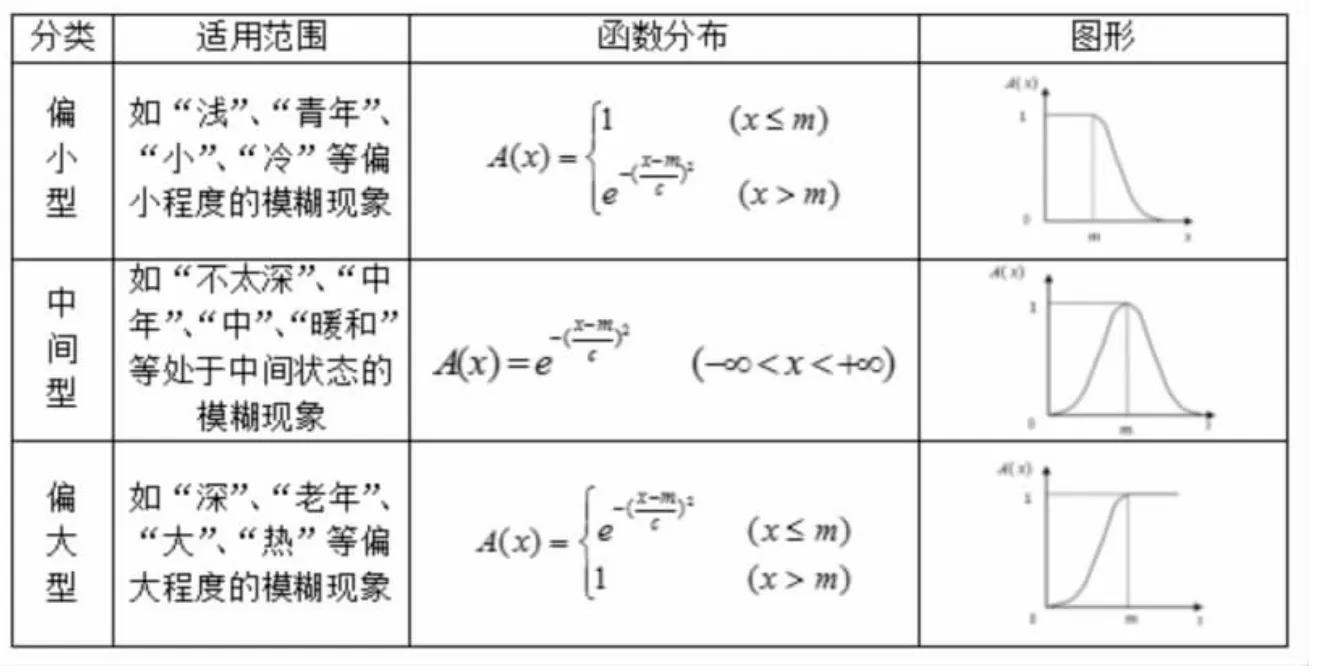
表1 正态型隶属函数的分布和图形

本文选定的定量指标中，除了“区域政务微博分布”指标属于成本型评价指标外，其余指标均属于效益型评价指标。分别给出效益型和成本型威胁等级评价指标的4个网络舆情预警等级分界值的计算方法，其中ek（k=1,2,3,4）分别表示轻度、中度、重度、特重网络舆情威胁预警等级。

(1)效益型威胁等级评价指标

令Nijl1为指标xijl对应e1的下界值；Nijl3为xijl对应e2与e3的分界值；Nijl5为xijl对应的上界值

令Nijl2为xijl对应e1与 e2的分界值；Nijl4为xijl对应e3与e4的分界值

(2)成本型威胁等级评价指标

令Nijl5为xijl指标对应e4的下界值；Nijl3为xijl对应e3与e4的分界值；Nijl1为xijl对应e1的上界值

令Nijl4为xijl对应e4与e3的分界值；Nijl4为xijl对应e2与e1的分界值

其中β为调节参数，将式（4）、（5）、（9）、（10）中的β取为黄金分割值，即β=0.618。

当xijl=mijlk时，隶属于ek的可能性最大，所以mijlk等于ek等级划分区间的中间值：

Nijlk和Nijlk+1分别为区间的上、下界限。由于两个威胁等级的隶属函数曲线在分界处交于同一点，令其近似等于0.5，即可得到ck近似值为

可得效益型定量指标xijl对于各级别的等级隶属函数如下

成本型定量指标xijl对于各级别的等级隶属函数如下

将以上4个隶属度归一化，得到定量指标xijl对于ek的最终隶属度为

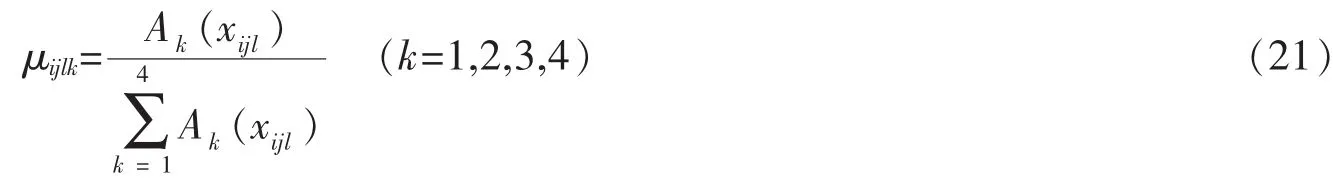
式（13）-（21）也适用于确定二级定量指标的等级隶属函数。将搜集整理的样本数据、近年来各省数据以及网媒的权威度分值均值代入上述方法，求得定量指标的预警等级划分标准，如表2；等级隶属函数的参数mijlk和cijlk，如表3。可得到每个指标的等级隶属函数。

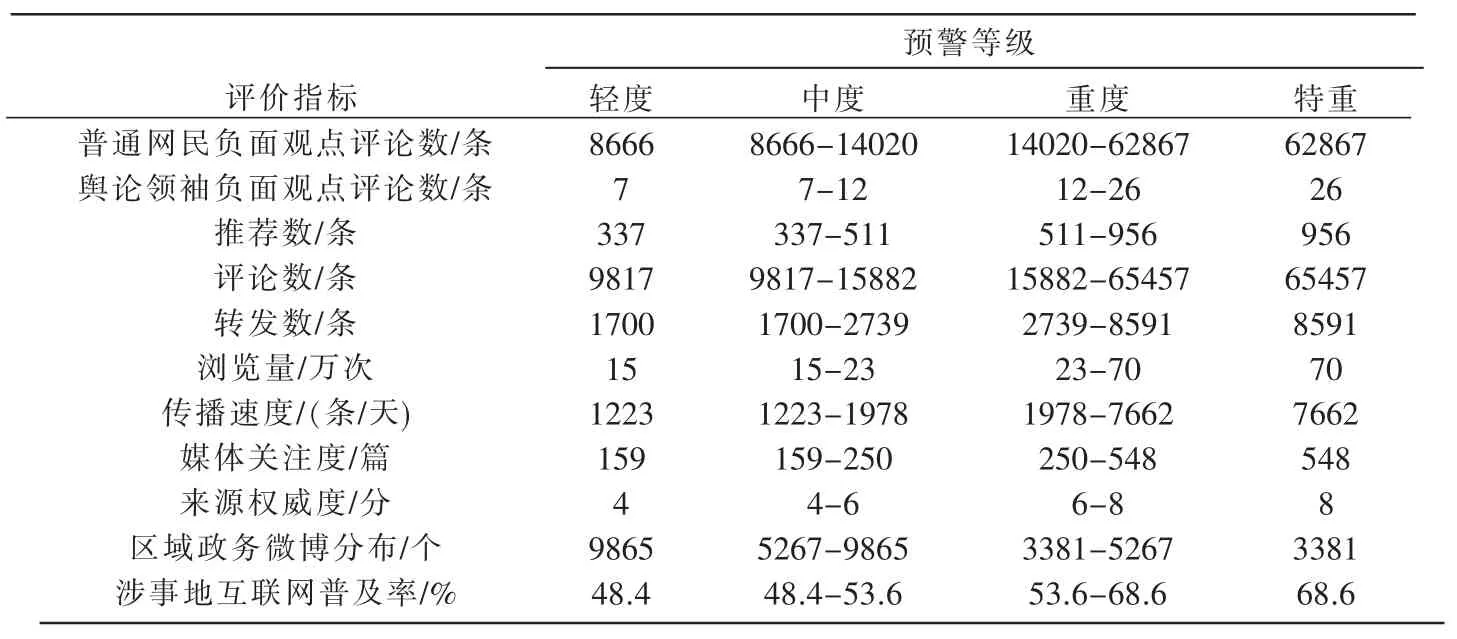
表2 网络舆情威胁预警等级的划分标准

表3 等级隶属函数中的参数和

2.2.2 基于直觉模糊相似度的TOPSIS确定定性指标等级隶属度

考虑到主观性，本文选用直觉模糊集来描述定性指标。考虑了犹豫度产生的影响，在Hong和Kim[13]提出的公式中加入了隶属度和非隶属度的差值，并用几何平均法进行修正。

设A和B是论域X={x1,x2,…，xn}上的2个直觉模糊集，A和B的距离为D（A，B），相似度为

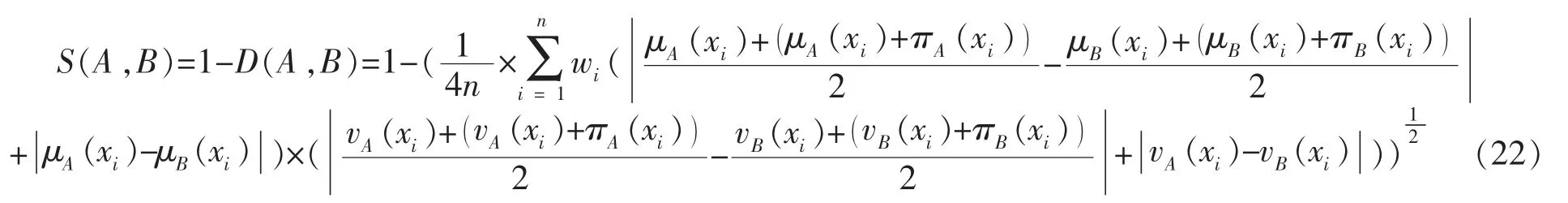
本文中的直觉模糊集只有1个元素，假设三级定性指标xijl在预警等级 ek（k=1,2,3,4）上的直觉模糊集为 Aijlk=<μijlk,vijlk>（k=1,2,3,4），威胁等级 ek上的正、负理想解分别是的相似度分别是。其中 μijlk、vijlk和 πijlk=1-μijlk-vijlk分别表示被调查者对指标xijl属于ek的支持、反对和不确定程度。则有

归一化后的最终隶属度为

式（23）-（26）也适用于确定二级定性指标的等级隶属度。

2.3 基于模糊AHP法和Choquet积分确定指标权重

2.3.1 构造模糊比较判断矩阵

本文采取更为粗略的三标度法，使问卷调查对象更容易接受并做出判断，减小由于人的主观性对评价结果造成的影响。对于模糊矩阵F=(fij)n×n，判断规则如下：

其中，C（i）、C（j）是指标 fi、fj的相对重要程度。

由于这样构造的模糊矩阵通常不具有一致性，需对进行如下调整：

（一）分别依据的行、列数值进行求和计算

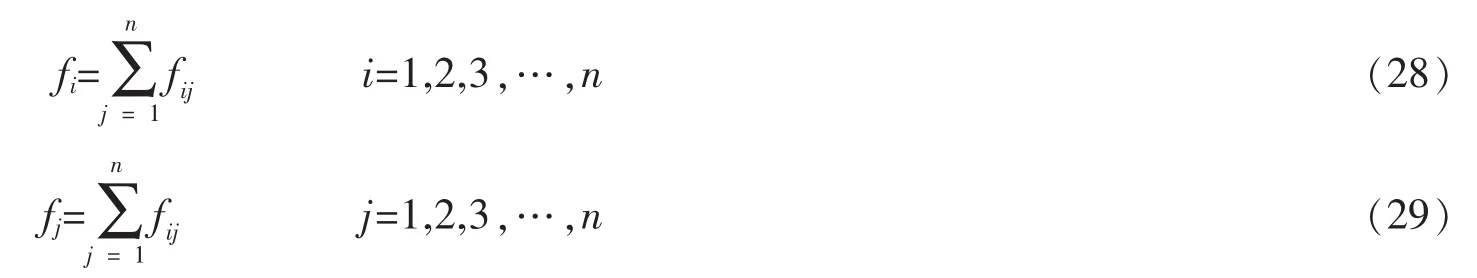
（二）对矩阵中的每个元素都进行模糊转换

2.3.3 计算指标权重

模糊转换后，需要进行一致性检验，而利用最优传递矩阵构造判断矩阵能够有效省略这一步骤。因此，本文采用式（31）计算以上所得模糊一致矩阵的最优传递阵D=(dij)n×n，其中

计算拟优一致矩阵F*

对于矩阵F*，求其最大特征根对应特征向量，归一化得指标权重wi。

2.3.4 基于Choquet积分中模糊测度的权重修正

对于威胁等级评价指标集 Xij={xij1，xij2，…，xijnii}若关于任意 j，z=1,2，…，ni且，j≠z，Xii∩Xiz=Φ 此时w满足

由式（35）可知，对于任意的，Aij∈P（xij）

对于某个三级威胁等级评价指标xijl∈xij，称w（xijl）是xijl的模糊测度函数，可以用它来衡量指标xijl的重要程度，即指标权重，简记为。由于 w（Xij）=1，根据式（35），代入 xijl的一组初始权重，可由式（37）确定唯一的参数 λ

因为 Aijl={xijl，xijl+1，…，xijnii}，Aijl+1={xijl+1，xijl+2，…，xijnii}，由式（36）可得

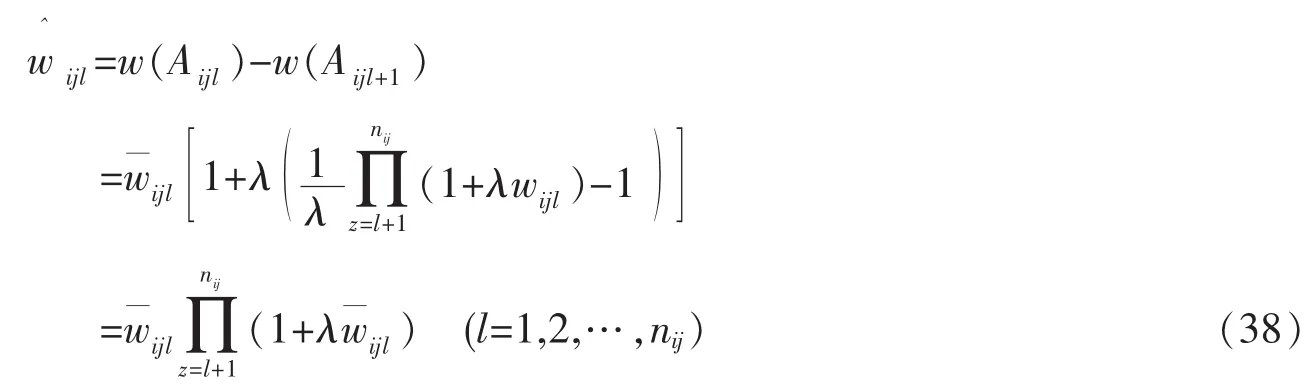
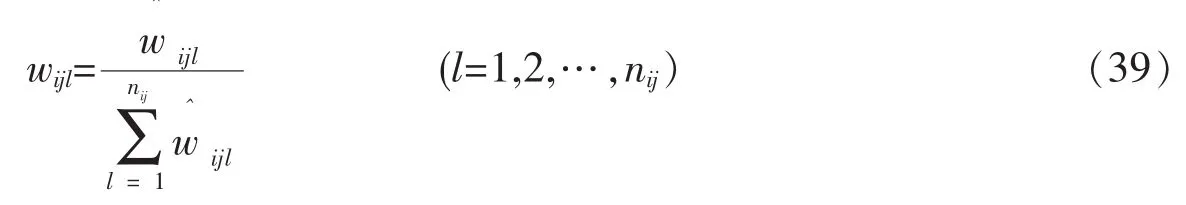
同理可求得二级、一级指标 xij、xi的最终权重为 wij(j=1,2,…，ni）和 wi(j=1,2,…，n）。

2.4 网络舆情威胁预警等级模糊综合评价方法

2.4.1 威胁预警等级模糊优选综合评价方法

考虑到相对贴近程度以及各指标对于各威胁等级的隶属度与最大、最小隶属度的偏离程度，本文选用模糊优选法代替传统模糊综合评价模型中的线性加权平均法，从而得到各威胁等级更加准确的隶属度。

下面以三级指标为例阐述方法。由于等级隶属度取值为[0，1]，本文设预警等级ek的正、负理想点分别为gk（gk=1）和bk（bk=0)。二级指标 xij对于ek的隶属度μijk与gk和bk的偏离程度用三级指标xijl对于ek的隶属度μijk与gk和bk的加权隶属度偏差次方之和来刻画，其中是距离参数，即

现用下式刻画μijk与gk和bk的远近程度，即

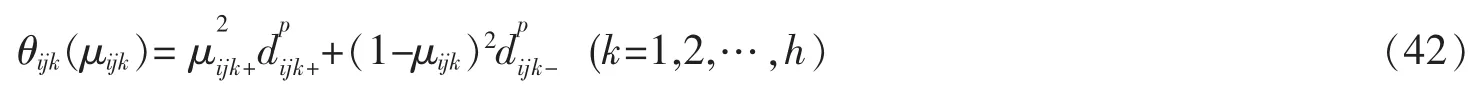
其中μijk、1-μijk分别是xij隶属于、偏离于ek的程度，将其分别看作为的权重。因此，θijk（μijk）可看作是的加权和。为了求得xij对于ek的隶属度μijk，运用最小二乘法。首先，建立如下目标函数

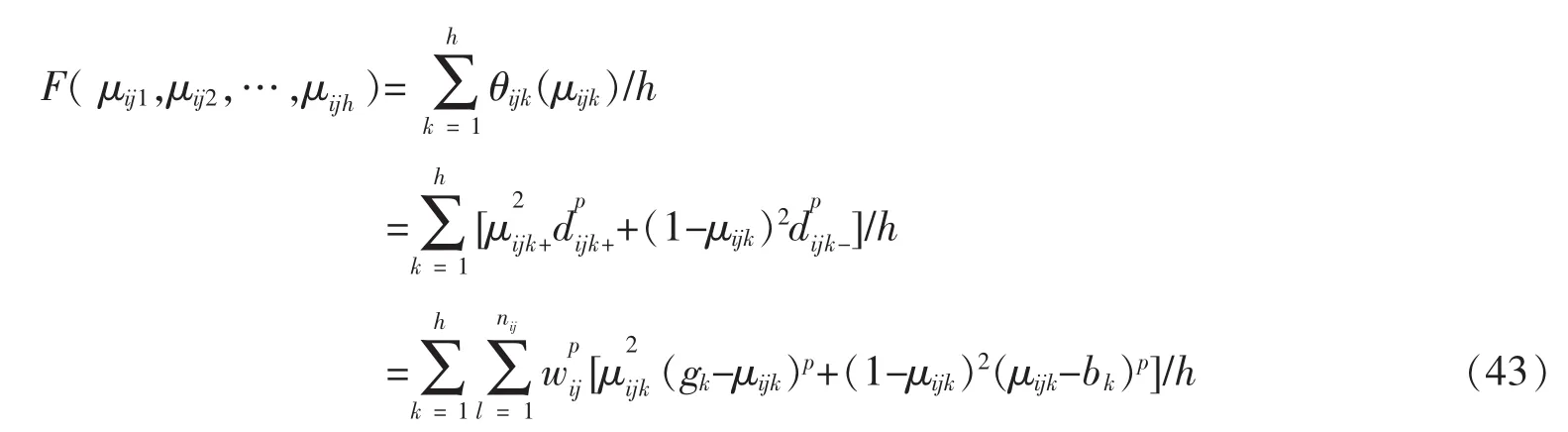
为了使目标函数取得最小值，对 F（ μij1，μij2，…，μijh）关于 μijk(k=1,2,…，h）求偏导，且令偏导为 0，即

同理，可求得指标xi对于ek的隶属度 μik为

最终，可求得该舆情事件对于威胁等级ek的综合隶属度k

归一化得到综合隶属度μk

2.4.2 基于模糊TOPSIS评价方法确定预警等级

假设：决策矩阵 U{μk}的正理想解为 U+=max{μk}、负理想解为 U-=min{μk}，其中 k=1,2,3,4。

3 模型应用与实例分析

本文以“洁洁良事件”作为案例，通过国家统计年鉴、百度指数、中国互联网络信息中心报告、八爪鱼数据采集器、蚁坊舆情报告、问卷调查等途径，采集舆情产生之日（2018年4月19日）至23日期间各威胁等级指标的数据，如表4、表5所示，对本文提出的网络舆情威胁预警等级模糊综合评价模型进行验证，验证过程如图2所示。

图2 模糊综合评价过程

表4 定量威胁等级评价指标数据

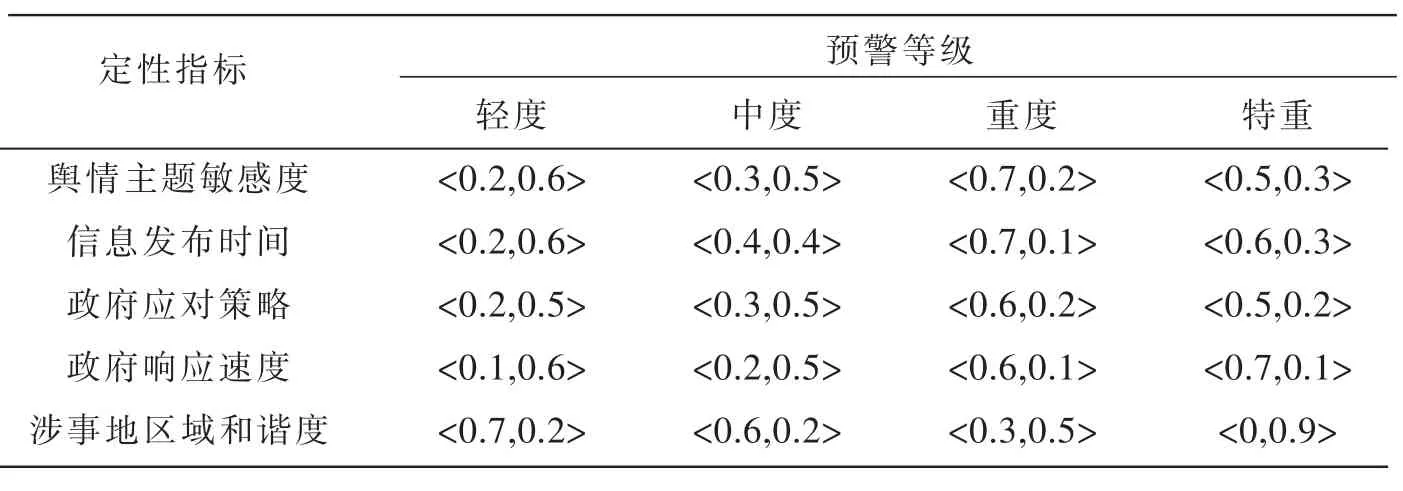
表5 定性威胁等级评价指标数据

将表4、表5中采集到的指标数据和直觉模糊集分别代入模型，最终求得该舆情事件相对于各威胁预警等级的等级隶属度为：

U={μ1,μ2,μ3,μ4}={0.002，0.078，0.439，0.481}

用模糊TOPSIS评价法对计算出来的4个综合隶属度进行排序，结果如表6所列

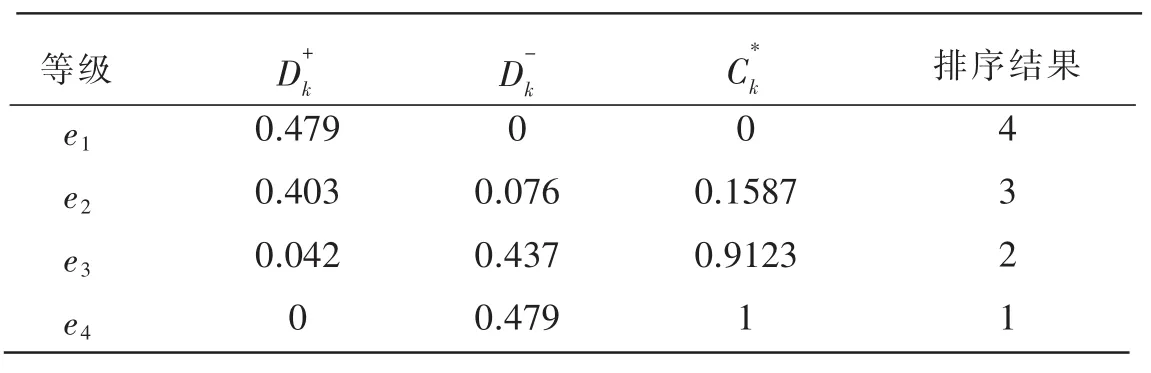
表6 利用模糊TOPSIS评价法得到的计算及排序结果

根据计算结果，可判断出该舆情所属的预警级别为红色预警，需引起警惕和及时进行防御。这与现实中“洁洁良事件”的网络舆情预警等级和4月24日舆情冲上了小高峰趋势大体一致。

对“洁洁良事件”使用线性加权平均法可求得关于各个威胁预警等级的综合隶属度为：

对以上综合隶属度取最大值，可判定其威胁预警等级为Ⅰ级特重警情。

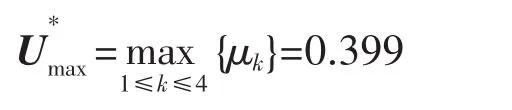
对其结果进行分析，最大隶属度0.399与次大隶属度0.342相差不多，此时选择最大隶属度对应的等级作为最终评判等级，难免会有丢失信息的风险以及给人造成一种“亦此亦彼”的不确定感。相比之下，本文采用的模糊优选评价法结合模糊TOPSIS评价法计算出来的综合隶属度和等级评判结果就避免了这一问题，更具有可信度和明确性。

4 结论

本文建立了从主体要素、客体要素、外部要素3个子系统出发的三级网络舆情威胁预警等级评价指标体系。选用正态型隶属函数求得定量指标的等级隶属度，利用基于直觉模糊相似度的TOPSIS法求定性指标的等级隶属度。然后，采用改良的模糊AHP法求出初始权重，并用Choquet积分模糊测度对其进行修正，得到最终权重。最后，利用模糊优选法和TOPSIS评价方法，构建网络舆情威胁预警等级模糊综合评价模型。该模型具有三个优点：

（1）用改良的模糊AHP法代替传统AHP法，利用最优传递矩阵构造判断矩阵，有效避免了一致性验证这一大计算量的环节，同时构造出来的判断矩阵也具有一致性的特点，效率高。

（2）运用三标度法代替传统AHP法中的九标度法构造对比矩阵，被调查者更容易接受，也更容易做出判断，尽可能地克服因为主观意识降低数据的可靠性这一缺点。

（3）因为考虑到最大隶属度原则存在只单纯比较隶属度相对大小，而对其之间具体的大小差距未作考虑的不合理之处，本文用TOPSIS评价方法代替最大隶属度原则，判断网络舆情威胁预警等级，能够得到更为准确、更贴近现实的预警等级。