水中声速测量实验的模型修正

沈 玥，周诗韵

(复旦大学 物理学系，上海 200433)

声速测量是大学物理实验的基本内容之一[1]，通常采用共振干涉法和相位比较法测量超声波的波长，乘以超声信号发生器的频率，即可计算得到超声波在特定介质中的声速. 该实验的基本原理为：发射换能器发出的声波与其在接收换能器上反射的声波相干叠加，当2个换能器间的距离等于半波长λ/2的整数倍时，形成驻波，接收换能器上声压波腹达到极大[2]. 当测量介质为空气时，增大接收器与发射器的距离，接收振幅的极大值单调减小，这表明需要考虑发射声波的波形、传播过程中的损耗以及换能器性能的影响[3-6]；当接收器与发射器非常接近时，原本相距λ/2的2次驻波共振极大值之间，出现振幅较小的“次极大”值. 这一现象产生的原因可能与信号源频率不纯导致“次频”共振[7-9]，声波在探头间多次反射[10-11]，以及换能器厚度带来的相位滞后[12]有关. 同样的方法可以用来测量水中的声速，例如研究声速与水溶液中介质浓度(如NaCl)的依赖关系[13]. 然而在水中，接收器的振幅及相位的变化规律与空气中不完全相同.

本文研究了水中声速测量实验中与原有模型不符的现象. 在介质为水的实验条件下，沿用空气中声波的多次反射模型[10-11]，同时考虑声波在水-空气界面处反射的影响，建立了水中声波的传播模型. 用Mathematica软件对模型进行数值模拟，并讨论了液面高度对模拟结果的影响. 模拟结果与实验结果相符.

1 实验现象与结果

1.1 实验原理和实验装置

从发射源发出的一定频率的平面波，经过空气传播到达接收器. 若接收面与发射面严格平行，当两者距离为半波长λ/2的整数倍时，入射波与反射波相干叠加形成稳定的驻波. 实验上，连续移动接收换能器，记录每次接收振幅极大或李萨如图呈直线时接收换能器的位置，即可通过线性拟合计算出超声波的波长λ. 声波波速v可表示为

v=νλ,

(1)

在已知超声波频率ν的情况下，即可计算出波速.

使用杭州大华仪器制造有限公司生产的SV-DH-7A声速测定仪进行实验，通过配套的SUX-6型信号发生器对发射换能器输入频率ν为37.850 kHz的正弦信号. 用固纬公司生产的双通道DS-1102A-U型示波器同时观察输入信号和接收换能器上获取的信号. 声速测定仪放置于45.3 cm×14.0 cm×12.4 cm的水槽内. 为考量水-空气界面对实验的影响，选择液面较低(水面距换能器中轴线35.0 mm)和液面较高(水面距换能器中轴线为61.0 mm)的2种情况进行测量.

1.2 异常现象

在水中声速的测量实验中，学生在处理实验数据时，通常以出现驻波时的探头间距离为y轴，数据的序号为x轴进行线性拟合，斜率即为半波长λ/2. 共振干涉法和相位比较法的拟合优度R2通常可达0.996，计算得到声速的测量值与标准值的相对偏差小于3%. 在实验中，学生观察到与理论预期不一致的“异常”现象，包括：

共振干涉法中，接收波振幅随2个换能器间距的变化情况如图1所示. 由于接收换能器增益可调，主要关注振幅的相对变化. 其中橙色点代表振幅主极大值，蓝色点表示振幅极小值. 由于示波器精度的限制，在一定范围内移动接收换能器，接收波振幅的变化都很小，图1给出了更多的数据点来描述主极大附近的振幅情况. 可以看到，共振干涉法的测量不确定度较大. 随着2个换能器距离的增加，接收振幅的主极大值并非单调减小，这与空气中的情况不同[5-6]. 图1中红色虚线表示振幅主极大的包络线，可以发现其谷值所对应的换能器距离与液面高度有关. 液面较低时，包络线在探头相距75 mm左右达到峰值，而在探头相距223 mm左右达到谷值. 增加液面高度，则包络线在探头相距180 mm左右达到谷值. 此外，也观察到了振幅“次极大”的现象，如图1中的红点所示. “次极大”现象在空气中也有发现，但是仅出现在换能器的间距小于50 mm处[10]. 而在水中，换能器间距大于230 mm，这一现象仍然存在.

相位比较法中，连续移动接收换能器并记录李萨如图呈直线时的位置. 对数据点进行线性拟合并观察其残差图. 如图2所示，残差图表现出二次曲线特征. 当液面较低时，残差图上凸，表明在水槽中部(约处160～200 mm)，每次需要移动换能器超过λ/2的距离，才能观察到李萨如图出现1次直线. 当液面较高时，残差图下凹，即在水槽中部每次只需移动小于λ/2的距离，就能观察到李萨如图出现一次直线. 实验中，相位比较法测得的数据点一般具有0.5 mm的不确定度，约是残差偏离范围的1/10，因此可以认为该实验方法具有系统误差. 需要说明的是，在共振干涉法中，主极大的位置不确定度为2～5 mm, 如图1所示，而拟合残差图的偏离范围也在±5 mm之间，因此不对共振法的残差图做分析.

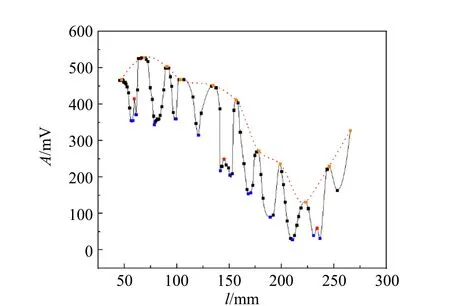
(a)液面较低

(b)液面较高图1 实验中测得接收振幅与接收器移动距离的关系

(a)液面较低

(b)液面较高图2 相位比较法实验残差图

2 模型建立

2.1 多次反射模型

图3给出了实验装置的示意图. 以发射器为原点建立坐标系，考虑声波的衰减，发射器发射的初始声波在t时刻被相距为l的接收器接收，则到达接收器时的初始声波为

(2)

其中,α为声波在介质中传时的衰减系数，A为超声波振幅，ω为角频率，λ为波长，φ0为初始相位.

图3 实验装置侧视示意图

考虑声波在换能器之间的多次反射. 假定Yn+1(t,l)是Yn(t,l)的反射波，当n为奇数时，超声波自接收器传播到发射器，而n为偶数时，自发射器传播到接收器. 接收器只能接收到所有下标为偶数的波列. 考虑声波在介质中的指数衰减，当探头相距较大时，Y6及其之后的反射波可被忽略，则接收声波可以表示为

(3)

其中Y2k(t,l)为

Y2k(t,l)=γ2kexp[-α(2k+1)l]·

(4)

在水中，声波波长变长，衰减系数变小，因此即便距离较远，声波在发射器与接收器之间多次反射的影响依旧不可忽略，多列反射波叠加造成了实验中观察到的次极大现象. 温度为26.0 ℃，大气压条件下，水中的声速为1 498.3 m/s[14]，实验中所用声波频率为37.850 kHz，则声波的波长为3.960 0×10-2m，为方便计算取λ=4.000 0×10-2m；换能器界面由铝制成，正入射时声压反射系数γ与界面两边介质的声阻抗Z1和Z2满足

(5)

这几列声波的频率是一致的，在数学上可以证明Y′(t,l)必可化简为A′cos (ωt+Φ)的形式，实验中接收波振幅即为Y′(t,l)的振幅A′. 为消除时间的影响，方便地得到A′的表达式，使其只为距离l的函数，可将Y′(t,l)先平方，对时间t做1个周期的积分，再除以周期长度T，即

(6)

平方是为了防止三角函数在t轴上下震荡导致积分值为0，由此可利用Mathematica模拟接收波振幅随接收器移动距离的关系如图4所示.

图4 振幅相对强度与探头距离的关系(多次反射模型)

该模型与共振干涉法中接收波声压随探头距离周期性变化的现象相符，并出现了振幅“次极大”. 然而该模型下声压极大值随距离是单调减小的，这与水中的实验现象并不相符，需要对该模型进行更多的修正.

2.2 液面反射模型

测量水中声速时，换能器并非处于无限大的水域. 如图3所示，其侧面和底面是水与有机玻璃水槽壁的交界面，上界面是水和空气的交界面. 换能器位于水槽中央，声波从水槽中线发出. 由于声源距各界面的距离与水中声波波长为同一数量级，因此需要考虑声波在各界面上的反射波对实验结果的影响.

空气声阻抗为425.8 kg/(m2·s)，有机玻璃的声阻抗为3.16×106kg/(m2·s)[14]. 由(5)式，假设声波正入射，计算可得上界面的反射系数为0.999，其余三面的反射系数为0.362，上界面的反射更为明显. 在实验中也发现，不改变换能器的位置，仅改变液面高度，示波器上李萨如图的形状也会改变. 这一现象说明上界面的反射对本实验有很大的影响. 仅考虑声波在水与空气的交界面上发生反射并到达接收器，如图3所示，可以写出到达接收换能器的反射波Yr为

(7)

定义d/2为界面到换能器中轴线的距离，则

(8)

考虑到斜入射时有效声阻抗并不严格与正入射时相同，并且存在能量耗散，在实际实验中反射声波的影响会更小，因此取反射波的权重因子W=0.9，略小于反射系数. 由于这列波不是垂直入射于接收器表面，接收器不能完整接收该列声波，因此在最后乘以cosθ. 于是，在仅考虑入射波和水-空气界面反射波的情况下，接收器处的声波为

Y′(t,l)=Y0(t,l)+Yr(t,l),

(9)

取d/2=50.0 mm，其余参量同上. 采用(6)式模拟接收波振幅随接收器移动距离的关系. 由于此时并未考虑声波在换能器间的任何反射，因此所得到的模拟结果无法体现声压的周期性变化，但可以得到主极大包络线的变化趋势.

在图5中，在约l=110 mm左右包络线达峰值，在l=240 mm左右处达到谷值，随后再次增大. 与图1(a)中主极大包络线的变化趋势相符合.

图5 振幅相对强度与探头距离的关系(液面反射模型)

3 讨 论

3.1 共振干涉法中参量d的影响

结合以上2种反射模型，接收器处声波为

(10)

设置与前文相同的参量，令d/2=50.0 mm，采用与(6)式类似的处理方法来模拟共振干涉法中接收波振幅随接收器位置的变化关系，如图6(a)所示. 可知当两换能器距离较近时(小于130 mm)，两次极大值之间出现了振幅较小的“次极大”，而“主极大”振幅的包络线先增大后减小再增大，呈非单调变化，这与图1(a)的现象一致. 此时，“主极大”包络线的谷值出现在换能器相距250 mm左右. 增大液面到换能器中心的距离，令d/2=65.0 mm，如图6(b)所示，包络线的谷值则出现在两换能器相距125 mm左右. 这与图1中包络线谷值位置随液面高度的变化趋势一致.

(a)液面较低

(b)液面较高图6 振幅相对强度与探头距离的关系(综合两种模型)

3.2 相位比较法中参量d的影响

(a)液面较低

(b)液面较高图7 相位比较法模拟结果的线性拟合残差图

利用Mathematica绘制参数方程

(11)

的函数图来模拟实验中的李萨如图，并考察参量d对相位比较法造成的影响. 令d/2取50.0 mm和65.0 mm来模拟液面较低和液面较高的不同状态，其余参量同前文. 记录李萨如图呈直线时对应的距离l，并进行直线拟合，所得残差图如图7所示. 当液面较低时，残差图上凸，而液面较高时下凹，这种特征与实验结果相符.

3.3 李萨如图的“多余”直线

在相位比较法中，如果只考虑理想模型，每当两换能器的相位差满足2kπ或(2k+1)π时，李萨如图都会出现直线. 此时换能器每次移动的距离是λ/2，随换能器的移动，直线的斜率左右交替. 然而实验中发现，有时会在换能器移动λ/2的距离内出现1次“多余”的直线，其倾斜方向与上一次直线相同，如图8所示. 相似的现象在空气中也有论述，但仅发生在接收器与发射器间距为λ以内时，其原因可能与声波的多次反射有关[15]. 在水中的实验时，这一现象仅在液面极低(水面距换能器中轴线25.0 mm)、两换能器间距170～200 mm之间观察到. 若增高液面，当水-空气界面高于换能器中轴线30.0 mm以上，该异常消失. 在之前的讨论中，实验上液面较低的状态对应水面距换能器中轴线35.0 mm，因此并未出现这一现象.

(a)l=173.82 mm

(b)l=182.35 mm

(c)l=196.05 mm图8 实验中观察到的李萨如图异常

在上面的讨论中，模拟取d/2=50.0 mm和d/2=65.0 mm时，没有观察到这一现象. 而当减小到d/2=40.0 mm时，便可观察到1次异常点. 如图9所示，当l=172.22 mm和l=197.01 mm时，李萨如图分别出现斜率为负和正的直线，两者出现的间距为24.79 mm，略大于λ/2. 在这2次位置中间，当l=178.38 mm时，李萨如图出现1

次“多余的”直线，斜率为负，与l=172.22 mm时相同. 这一结果与图8的现象一致. 其原因是液面反射波中Yr(t,l)非线性变化的相位干扰. 随着液面增高，反射波影响减小，异常现象消失.

(a)l=172.22 mm

(c)l=197.01 mm图9 模拟结果中的李萨如图异常

4 结 论

用共振干涉法和相位比较法测量水中的声速，发现了不同于理论预期的异常现象. 考虑声波在接收和发射换能器间的多次反射，以及声波在水-空气界面的反射，建立了实验模型，并应用Mathematica进行模拟. 模拟结果可以显示：共振干涉法中，两换能器间的多次反射引起了振幅“次极大”的出现. 液面反射波与正常传播的波列的相位差，决定了接收声波在特定位置上相干相长或相干相消，引起了振幅主极大的非单调变化. 这一相位差与水面高度有关，因此水深不同，相干相消的位置也不同. 由于液面反射波引入了非线性变化的干扰相位，使接收波列的相位变化更为复杂，导致了相位比较法的系统误差：当水深增加时，残差图从上凸变为下凹. 而特别的，当液面特别低时，模拟中观察到了李萨如图的“多余”直线. 本文的模型较好的解释了水中声速测量实验中的诸多现象.