高含水油田多相混输管道水力计算方法研究

李玉春 谢丽香 兰乘祎 张淼

1大庆油田工程有限公司

2大庆油田矿区事业部

3大庆油田天然气分公司

管道输油在油田生产过程中具有重要的作用，出于降低投资、节约运行成本的目的，油田现场大多采用油气水混输的方式进行输油[1-2]。准确预测油气水三相流管道的压力损失，能够为管网的合理设计提供理论支持，为相关设备的选型提供科学指导，为运行方案的优化调整提供可靠依据。因此对三相流管道的水力计算方法进行研究，构建符合现场实际的三相流压降模型具有十分重要的工程意义。

近年来，油气水三相流水力计算方法的研究逐渐得到重视，众多学者对三相流水力计算方法的研究可以归纳为两类：从已有的气液两相流压降模型的角度出发进行研究；从力学角度出发，对不同相态之间的作用力进行研究。后者虽然能够较好地描述三相流流动的作用机理，但是计算过程较为繁冗、复杂，在工程实践中难以推广，故油田现场在计算油气水三相流管道的水力分布时大多使用气液两相流压降模型[3]。目前气液两相流的压降计算方法主要包括三种[4-5]：均相流模型压降公式、分相流模型压降公式、流型模型压降计算法。

随着油田开发的深入，含水率逐渐上升[6]，与开发之初相比，高含水油田采出液的流变特性已发生显著变化，在计算其水力分布时，如果使用传统的气液两相流压降模型将会产生较大的误差，故需结合现场实际对多个模型进行验证，选择出最合适的方法[7]。本文以高含水油田多相混输管道为研究对象，首先收集混输管道的基础参数、运行参数；然后选取均相流压降公式中的杜克勒I法，分相流压降公式中的杜克勒II法，流型模型压降计算法中的Beggs-Brill法、Baker法分别对管道压降进行计算并对比各模型计算精度；再结合实际运行参数，基于最小二乘法对精度最高的水力模型进行修正，使其更适用于现场实际管道的压降计算；最后采用单因素敏感性分析方法，分析混输管道压降对不同运行参数的敏感性。

1 水力计算方法

1.1 杜克勒Ⅰ法

在这一方法中，管内的混合流体被杜克勒等视为气液两相之间无滑脱的均匀混合物，则此时的持液率（真实含液率）可按照体积含液率的计算方法进行计算[8-9]。在求解压降过程中，单相流体的物性参数应替换为气液混合物的物性参数。此方法的压降计算公式为

式中：Δp为混输管道总压降，Pa；λ′为无滑脱阻力系数；L为管道长度，m；d为管道内径，m；ρm为无滑脱时气液混合物密度，kg/m3；um为气液混合物流速，m/s。

1.2 杜克勒Ⅱ法

在这一方法中，管内的混合流体被杜克勒等视为气液两相之间是有滑脱的（即气液两相流速不等），但液相速度与气相速度间的比值沿管长保持不变[10-11]。与杜克勒Ⅰ法相比，杜克勒Ⅱ法在气液混合物密度计算、阻力系数计算这两方面有所改进。

在计算气液混合物密度时，杜克勒等借鉴相似理论，认为有滑脱时气液混合物的平均密度应按式（2）计算。

式中：ρm为气液两相之间有滑脱时混合物的平均密度，kg/m3；ρL为液相密度，kg/m3；ρg为气相密度，kg/m3；RL为体积含液率；HL为持液率，需要根据体积含液率、气液混输雷诺数之间的关系，利用循环迭代的方法进行求解。

在计算阻力系数时，杜克勒等根据数据库中的实测数据，绘制了关于有滑脱阻力系数的关系曲线，如图1所示。

图1 λ λo 与RL 的关系曲线Fig.1 Relation curve betweenλ λo and RL

图1中λ为有滑脱阻力系数；λo为单相液体流动时的阻力系数；纵坐标为λ与λo的比值；横坐标为体积含液率。

当求得单相液体阻力系数与体积含液率时，可通过图1查找有滑脱阻力系数。与杜克勒Ⅰ法相比，杜克勒Ⅱ法的计算过程相对复杂，但是在各个方面的适用范围都更广一些。

1.3 Beggs-Brill法

Beggs-Brill法的压降公式为[12-13]

式中：g为重力加速度，m/s2；θ为管道倾角，(°)；λm为气液两相混输阻力系数；Gm为气液两相质量流量，kg/s；为平均压力（绝对压力），Pa；usg为气相表观流速，m/s。

在Beggs-Brill法中，持液率的确定方法是重点，在其计算过程中需要先根据体积含液率、弗劳德准数判断管道内气液两相流的流型，然后再根据流型确定持液率的计算公式。

1.4 Baker法

Baker法中压降公式为[14-15]

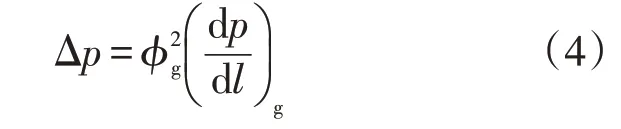
在Baker法中，分气相折算系数的计算方法由流型决定，故流型的确定是使用Baker法计算混输管道压降的关键。

2 水力模型精度对比

使用以上模型对K1-K2、T1-T2、C1-C2油气水三相流管道的压降进行计算，50 ℃时管内原油的密度为862.68 kg/m3，黏度为39.35 mPa·s，各管道基础参数如表1所示，运行参数如表2所示。

表1 管道基础参数Tab.1 Basic parameters of pipeline

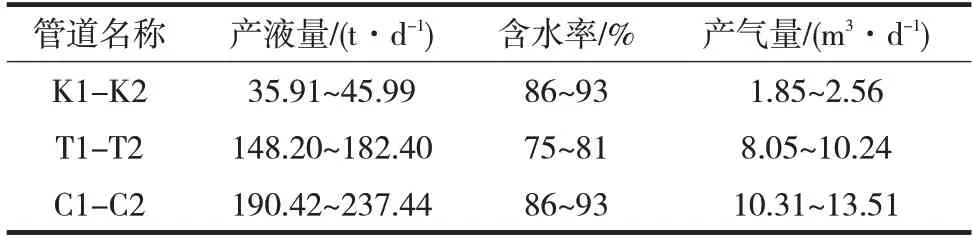
表2 管道运行参数Tab.2 Operation parameters of pipeline

将计算值与收集到的实际值进行对比，可得不同模型的误差分析结果（图2）。

图2 各压降模型计算精度对比Fig.2 Comparison of calculation accuracy of each pressure drop model

误差分析结果表明，在以上压降计算方法中，杜克勒Ⅱ压降模型的计算精度最高，杜克勒Ⅰ法和Beggs-Brill法次之，Baker法的计算精度最低。故选取杜克勒Ⅱ法作为高含水油田多相混输管道的水力计算模型。

3 模型修正与验证

杜克勒Ⅱ法虽较其他压降模型的计算结果更接近实测值，但其精度也尚未达到工程要求，故需结合现场实测数据对杜克勒Ⅱ压降模型进行修正。分析杜克勒Ⅱ法可知，在求解压降的过程中需要用到管道规格、气液相流量、气液相物性、混输阻力系数等相关参数。其中管道规格和流量等参数为固定值，气液相物性由管道温度、压力确定，而混输阻力系数受流速、介质密度、黏度、持液率等多种因素影响。因此可对混输阻力系数进行修正以提高杜克勒Ⅱ法的计算精度，即根据收集到的实测数据反算出实际阻力系数，然后对理论阻力系数、实际阻力系数间的数学关系进行回归。

基于最小二乘法，结合K1-K2、T1-T2管道多组实测数据对混输阻力系数进行修正，得到混输阻力系数修正式为

式中：λm为修正后的混输阻力系数；λm1为混输阻力系数理论值。

将混输阻力系数修正式代入原模型中，得到修正后的压降模型为

为进一步验证修正后杜克勒Ⅱ压降模型的计算精度，现使用该模型计算K1-K2、T1-T2、C1-C2管道的终点压力。各管道终点压力理论值、修正值、实测值如图3、图4和图5所示。

图3 K1-K2管道终点压力对比Fig.3 Comparison of terminal pressure of K1-K2 pipeline

从图中可以看出，使用修正后水力模型计算得到的终点压力更接近实测值。模型修正后K1-K2管道、T1-T2管道、C1-C2管道终点压力计算值与实测值之间的平均相对误差分别为8.82%、9.69%、9.71%。对全部数据进行统计后发现，水力模型修正后其计算值与实测值间的平均相对误差为9.45%，其精度能够满足工程需要，符合工程实际应用条件。由此可见，对成熟的气液两相流压降模型进行优选，然后结合现场实测数据改进优选出的压降模型是分析油气水三相流管道水力特性的合理途径。

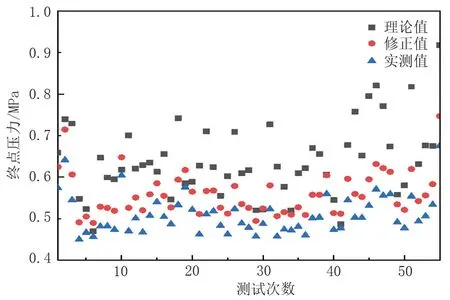
图4 T1-T2管道终点压力对比Fig.4 Comparison of terminal pressure of T1-T2 pipeline

图5 C1-C2管道终点压力对比Fig.5 Comparison of terminal pressure of C1-C2 pipeline

4 混输管道压降敏感性分析

明确不同因素对混输管道压降的影响程度，对现场运行方案的调整具有重要的实际意义。现采用单因素敏感性分析方法，分析混输管道压降对各个运行参数的敏感性。所谓单因素敏感性分析，指的是对单个不确定性因素的变化所引起的系统特性的变化进行分析，即假设某系统的系统特性P主要由n个因素a={}a1,a2,…,an所决定，则有，规定时系统处于基准状态，此时系统特性为P*，分别使各因素在各自的允许范围内变化，并分析这些因素的变化所引起的系统特性P偏离基准状态下系统特性P*的程度。鉴于在实际工程中，决定系统特性的多个因素往往是量纲各不相同的物理量，故需要进行无量纲化处理[16]。首先，将敏感度函数Sk(ak)定义为系统特性P的相对变化与因素ak的相对变化的比值，则有

根据式（7）可绘制ak的敏感度函数曲线Sk-ak。取，可得到因素ak的敏感度因子为

由敏感度因子的确定方法可知，各因素的敏感度因子皆为无量纲非负实数。的值越大，表明在此基准状态下，系统特性P对因素ak越敏感[17]。若φk(ak)为分段函数，则在分段点处有可能出现导数不连续的情况，此时可使用函数拟合技术消除导数不连续点。

现以K1-K2混输管道为例，分析混输管道压降对不同影响因素的敏感性。首先统计该管道的运行数据，删除数据坏点，然后取各参数的平均值为基准值，得到各影响因素基准值，如表3所示。

表3 基准参数集Tab.3 Basis parameter set

以分析混输管道压降对产液量的敏感性为例，令其他影响因素取基准值保持不变，qL在其允许的波动范围内变化，此时系统特性为

式中：qL为产液量，t/d；为基准状态下产气量取值，m3/d；φ*为基准状态下含水率取值，%。

分析式（9）即可明确系统特性ΔP对影响因素qL的敏感性，则敏感度函数为

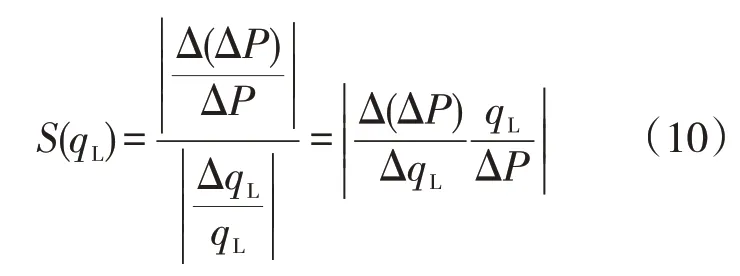
由式（10）可绘制产液量qL的敏感度函数曲线（图6），重复以上计算过程，可绘制其他运行参数的敏感度函数曲线（图7、图8）。

从图中可以看出，在当前波动范围内，产液量、产气量、含水率的敏感度均随自身的增加而变大。当qL=37.96 t/d时，可得产液量的敏感度因子为=1.951 3；当qG=2.16 m3/d时，可得产气量的敏感度因子为=0.02；当φ=90%时，可得含水率的敏感度因子为S(φ*)=0.442 4。敏感性分析结果表明，对油气水混输管道压降影响程度由强到弱的运行参数分别为产液量、含水率、产气量。

图6 产液量的敏感度函数曲线Fig.6 Curve of sensitivity function of liquid production

图7 产气量的敏感度函数曲线Fig.7 Curve of sensitivity function of gas production

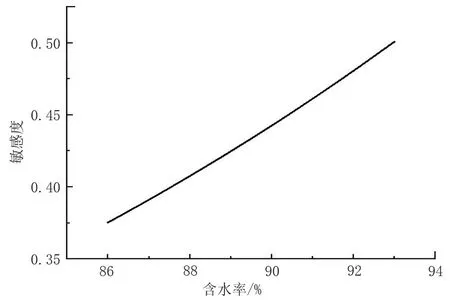
图8 含水率的敏感度函数曲线Fig.8 Curve of sensitivity function of water cut

5 结论

（1）以高含水油田多相混输管道为研究对象，使用杜克勒Ⅰ法、杜克勒Ⅱ法、Beggs-Brill法、Baker法四种压降模型分别计算了管道压降，并对计算结果进行了误差分析。误差分析结果表明，在计算高含水油田油气水三相流水平管道的终点压力时，杜克勒Ⅱ法的计算精度最高。

（2）利用现场管道的多组运行参数反算出多个实际阻力系数，基于最小二乘法对理论阻力系数、实际阻力系数间的数学关系进行了回归，然后将回归的数学关系式代入原模型中对原压降模型进行了修正。经统计，模型修正后终点压力计算值与实测值间的平均相对误差可降至9.45%，符合工程实际应用条件。

（3）采用单因素敏感性分析方法分析了油气水三相流管道压降对不同运行参数的敏感性。敏感性分析结果表明，在一定波动范围内，对高含水油田多相混输管道压降影响程度由强到弱的运行参数分别为产液量、含水率、产气量。