微分几何中一般曲面的若干性质的进一步探讨

王 文，齐继兵，余 静

(合肥师范学院 数学与统计学院，安徽 合肥 230601)

1 前言

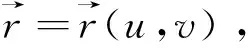
2 由显函数和隐函数所确定的曲面上点的分类条件

曲面上的点可根据它的Dupin指标线分为四类：椭圆点、双曲点、抛物点和平点。由该点处的第二类基本量间的关系给出四类点的判定条件，如下：

引理1[1]设P曲面S上任一点，则

(1)若LN-M2>0，则该点为曲面的椭圆点；

(2)若LN-M2<0，则该点为曲面的双曲点；

(3)若LN-M2=0，则该点为曲面的抛物点；

(4)若L=N=M=0，则该点为曲面的平点，此时Dupin指标线不存在.

(1)若detD(P)>0，则P点是椭圆点；

(2)若detD(P)<0，则P点是双曲点；

(3)若detD(P)=0，则P点是抛物点；

(4)若矩阵D(P)为零矩阵，则P点是平点。

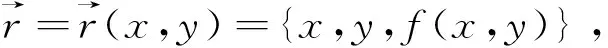
由第一类基本量的计算公式可得

E=1+a2,F=ab,G=1+b2

(1)

另外，曲面S的法向量为

再由曲面的第二类基本量的计算公式可得

(2)

所以

(3)

再根据引理1即可得结论成立。

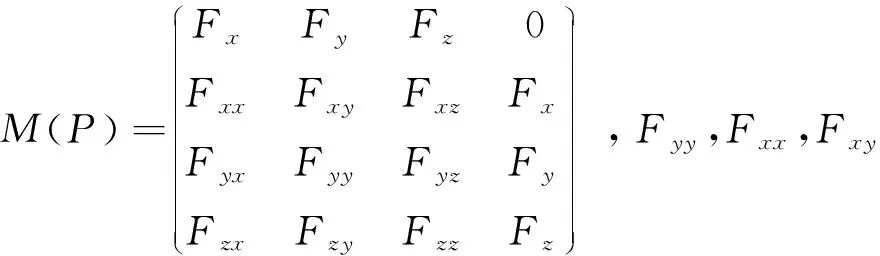
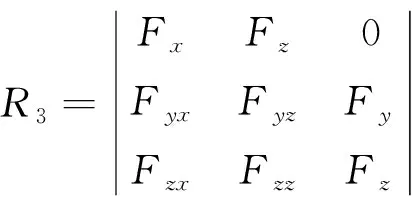
(1)若detM(P)>0，则P点是椭圆点；

(2)若detM(P)<0，则P点是双曲点；

(3)若detM(P)=0，则P点是抛物点；

(4)若R1=R2=R2=0，则P点是平点。

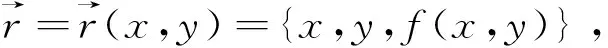
根据《数学分析》[2]中隐函数求导法则，可得

(4)

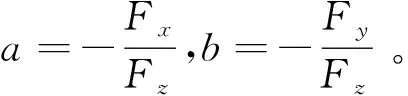
再对方程(4)式两边分别对x和y求偏导数，并由混合偏导数相等，得

Fxy+Fxzfy+Fyzfx+Fzzfxfy+Fzfxy=0,

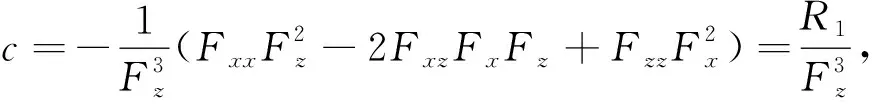
再由(2)可得第二类基本量为

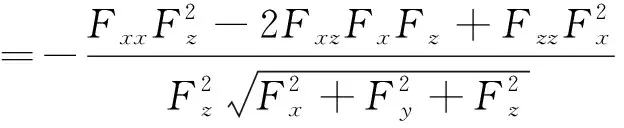
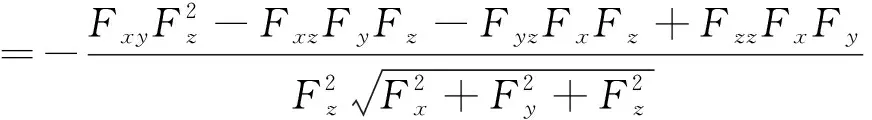
所以

(5)

下面证明

(6)

事实上，

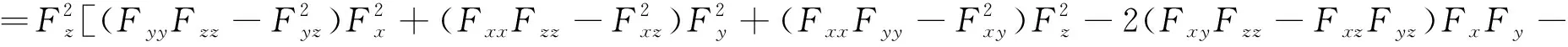
因此，(6)式成立。再由(5)和(6)即可得结论成立。

3 可展曲面的充要条件

引理2[1]一个曲面是可展曲面的充分必要条件是它的高斯曲率为零。

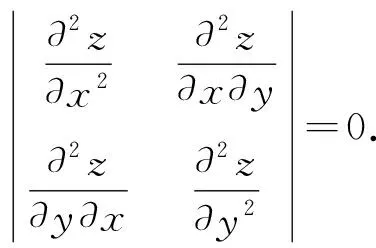
由高斯曲率计算公式 和(3)得

再由引理2即可得证。

证明：由公式(5)，(6)以及高斯曲率计算公式可得

结合引理2可得K=0⟺detM(P)=0。因此定理得证。