缔造思辨课堂，绽放个性精彩

倪琴

思辨能力是数学课程学习的关键能力，指一个人辩证思维、独立思考的能力，将这一能力的培养落实到教学中，不仅能调动学生思维，激发其探究兴趣，还能提升学生核心素养，让其在丰富的课堂活动中培养逆向思维、辩证思维以及独立思考能力，以此促进学生全面发展。

一、创设问题情境，激活思辨

问题是教学的线索，更是思维的起点，在课堂上借助问题情境不仅能激活学生思维，调动其兴趣，还能激发学生思辨的潜能，让其在问题探究中培养独立思考、辩证分析的能力，以此为后续学习奠定基础，开启数学智慧大门。

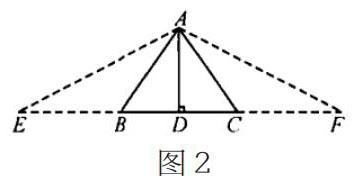
例如，在“等腰三角形的判定与性质”复习课上，结合重点内容，我设计了这样一道题：如图1，AD是△ABC的边BC上的高，在下面条件中选择一个，由此判断出△ABC是等腰三角形：①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD。先让学生独立思考，再在班级交流。对于三个选项，学生首先排除①，这时就可提问：为什么？思考片刻后，学生没有直接阐述原因，而是从反面论证：在①正确的情况下，能得出的结论是∠BAD+∠CAD=90°，随即便可得出∠BAC=90°，那么△ABC是直角三角形，不能判断它是等腰三角形。对于②，学生没有什么争议，在简单推理证明后很快得出是等腰三角形的结论。对于③，学生没有马上得出结论，这时要给其留出分析的空间。随后，学生作图思考（图2），得出结论：延长DB至E，使BE=AB，延长DC至F，使CF=AC，连接AE，AF，因为AB+BD=AC+CD，由此可得出△AEF是等腰三角形的结论，在这一基础上进一步推导，便可得出△ABC是等腰三角形。在这一过程中，学生灵活转化，将AB+BD=AC+CD转化为ED=FD，十分巧妙。教学至此，让我觉得十分惊喜。

问题情境的设计要围绕开放题展开，给学生提供较大的思考空间，让其在现有条件中挖掘，在不断深入中掌握要点，由此解决问题，促进学生思辨能力的培养。

二、巧用课堂追问，演绎思辨

有效的课堂要注重学生思维的培养，借助互动引发思考，让学生的思维从狭隘走向广阔，由肤浅走向深刻，以此寻找生长点，促进教学达到理想效果。要结合实际巧用追问，让学生在探究中提升，促使课堂走向高效。

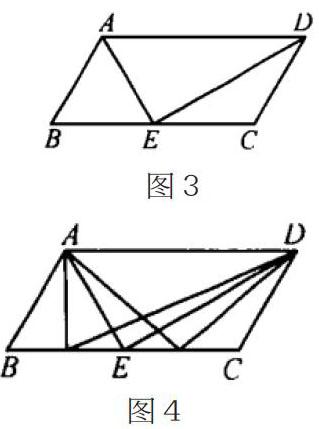
例如，在“平行四边形”的复习课上，结合重点，根据学生实际，我设计了这样一道题：如图3，在平行四边形ABCD中，AD=2AB，E是BC的中点，求证：∠AED=90°。让学生自主思考，在简单交流后，进一步引导：把握住问题的关键，即“E是BC的中点”得到∠AED=90°的结论，那么在BC上还有没有其他这样的点（如图4），也能得到这一结论？至此，学生看法不一，有的认为没有，有的迟疑、犹豫，还有的学生认为这样的点不止一个，但是却不知道怎么求。基于學生现有认知的限制，这时就要引导学生运用“轴对称”的思想来处理。学生被启发后，对于这个问题有了崭新的认识，其中有一个学生这样回答：“我尝试将△AED沿着AD的中垂线对折得到△AE'D（如图5），这样就得到第二个点了。”根据这一思路，学生将图画出来，随后便恍然大悟。这时，不妨再追问：是不是在任何情况下，BC上总有两个点使得∠AED=90°？可开展小组交流，让学生在讨论中分析“BC上有2个还是1个这样的点与∠B的大小有关”。

学生经历了发现问题、提出问题、探究问题以及解决问题的过程，初步感知到了探究学习的魅力。在这一过程中，要突出学生主体，发挥其主观能动性，让其在问题的驱动下不断深入，由此促进思维发散，让其体会到思辨的快乐。

三、借助反证求解，促进思辨

通常，人们在思考问题时会采取正向思维，即由因索果。然而，在面对一些较难且灵活的问题时，这种思路是行不通的。因此，教师就要引导学生运用反证法解决问题，让其在间接证明中解决问题，由此反向思考，促进学生发散能力及逻辑能力的提升。

在设计教学时，不急于运用反证思路解决问题，要先举例让学生明白这一思路，在理解的基础上尝试运用，由此加深对要点的掌握。例如，在教学“平行线的性质”时，推出“两条平行线被第三条直线截得的内错角之间的关系”时，教材就运用了反证法。对于这一点就可引导学生阅读，让其在自主思考中加深对这一思路的理解，由此内化。随后，在总结归纳时，可梳理基本思路，即“反设—归谬—存真”。在这一基础上，讲解“点和圆、直线和圆的位置关系”时，就可引导学生运用“反证法”思考，在实践探究中意识到“经过同一直线的三个点不能作圆”。借助这一过程，不仅能加深学生对数学要点的理解，促进其知识体系的完善，还能对原有解题方法进行扩充。在引导运用时，对于一些特殊的问题，可先让学生提出一个反面的假设，随后根据假设所推导出的结果与事实矛盾，说明原先的假设错误。这样一来，学生便能在解题中理解反证法的原理，掌握反证法的步骤与具体操作，以此锻炼数学思维能力，有效提升教学效果。

反证法的引入与运用突破了传统单一教学，将学生从机械解题中解脱出来，引导其从反面思考问题，在获得启发后逐步深入，以此获得更深刻的认识。在这一过程中，要充分调动学生，激发其兴趣，让其在训练中锻炼思维，提升综合素养。

四、组织交流活动，提升思辨

学生思辨能力的培养与发展不是一朝一夕能实现的，需要日复一日的坚持，借助各种各样的活动引导，以此激发思维，在不断调动与提升中落实。意识到这一点，教师在设计教学时就不能忽略交流活动，要从不同角度展开，让学生在参与中实现提升。

学生思维能力与认知水平受到很多因素影响，在面对同一个问题时往往会产生不同看法，这时就要注重对其创新性思维的培养，充分尊重学生的不同想法，让其在问题解决中释放个性，以此落实教学，促使课堂达到预期效果。对于观点不同的学生要给予鼓励，引导其向正确的方向思辨，避免言语上的冲突。交流活动结束之后，要注意归类总结，引导学生回顾整个过程，让其在活动中提升素养，为后续学习打下基础，以此完善认知，长此以往，就能培养学生逻辑能力，促使其在一定时间内掌握一种解题方法。在这一过程中，可适当选择一些相关的习题，让学生在具体操作中体会这种方法，逐步内化，在之后的训练中灵活运用。

总之，初中生思辨能力的培养是数学教学的重要内容，将其落实到教学中，不仅需要我们的耐心指导，更离不开学生的主动探索与积极训练。意识到这一点，就要着眼教学，灵活引导，让学生在实践中思考，在探究中提升能力、素养。