三角形-椭圆复合微孔织构化机械端面密封性能的数值研究

魏 伟 ，陈 思 ，章亦聪 ，吴玉国 ，王 涛 ，3，时礼平 ，3，4

（1.安徽工业大学 机械工程学院，安徽马鞍山 243032；2.安徽工业大学科研处，安徽马鞍山 243032；3.特殊服役环境的智能装备制造国际科技合作基地，安徽马鞍山 243032；4.特种重载机器人安徽省重点实验室，安徽马鞍山 243032）

众多研究表明，利用物理、化学等工艺方法在密封端面加工出具有一定形状、尺寸的表面微织构，可有效改善机械密封端面的摩擦学性能［1-3］。其机理可归结为：通过设置在密封端面的微织构，并借助动、静环的相对转动，在两密封端面间形成具有微米尺度的润滑油膜，促使两端面分离而实现动、静环的非接触，进而减小密封配副间的摩擦与磨损［4-6］。

对于微孔方向特性的数值模拟方面已开展广泛研究。佘宝瑛等［7］针对圆形、菱形、椭圆形和长方形4种织构化端面的密封性能进行了研究，发现方向型微孔对端面密封性能的影响显著；于海武［8］对比考察了圆、椭圆、三角形微孔及具有不同排布特征表面的润滑性能，结果发现椭圆织构化表面具有最优的减摩效果；杨笑等［9］建立了不同方向型微孔织构化端面在混合润滑状态下的热弹流理论模型，继而分析了不同形状端面在稳态运行下的流体膜压力、膜厚和端面温度的变化规律；宋国峰等［10］基于平均流量模型和微凸体接触模型，研究了方向性微孔对润滑状态转化的影响，并分析了法向载荷、润滑油黏度、表面粗糙度、方向因子等对摩擦学性能参数的影响。王菁等［11］分别在水润滑和油润滑的条件下研究了倾斜方向性微孔表面润滑的温升特性，并对比分析了光滑表面下圆形和倾斜椭圆微孔表面的分布方式和开孔率对摩擦因数和润滑温升的影响规律。

对于方向性微孔织构化端面密封性能的研究，以三角形微孔织构和椭圆微孔织构化端面的研究较多。吉华等［12］结合流体楔效应理论采用数值计算的方法通过建立Fluent多相流空化模型研究等边三角形微孔端面机械密封的几何特性对泄漏率和开启力的影响；李茂元等［13］建立了均匀分布的等腰三角形微孔端面理论模型，通过有限差分法利用流体动压润滑方程对流场进行了数值求解，并获得了无量纲压力分布。张科等［14］采用数值解析法对机械端面椭圆微孔的方向角所引起的几何特性参数进行了分析，并研究其密封泄漏率与几何收敛点的关系；石卓等［15］基于Navier-Stokes方程，建立单一椭圆型微孔端面不可压缩牛顿流体的三维动力润滑模型，深入探讨了机械密封椭圆微孔端面的动力润滑性能。上述结果证实了三角形、椭圆微孔表面织构在改善机械端面密封性能方面所具备的优越性。

对于复合表面织构密封性能的研究成果则相对较少。Wang等［16-18］在制备单一微孔、复合微孔织构的基础上，系统考察了不同面积率及深径比条件下的织构化表面的承载能力，结果表明，复合织构化表面的极限载荷可提高近39%。因此，为了丰富微孔织构化端面密封的研究成果，基于目前研究，本文选取密封性能较好的三角形微孔织构和椭圆微孔织构创新性地提出三角形-椭圆复合织构化机械密封端面，并与单一三角形微孔与单一椭圆形微孔进行比较，考察不同结构参数、操作参数对密封性能的影响，以期为表面织构的创新设计及拓展应用提供借鉴。

1 理论模型

1.1 几何模型

机械端面密封的基本结构包括一对平行对置的并发生相对旋转的动、静环［19-22］，动环表面加工有微孔织构如图1所示。rin，rout分别表示动、静环内、外径，n表示动环旋转速度，hp表示织构深度，h0表示密封间隙。

图1 微孔织构化机械端面密封

在动环表面配置三角形-椭圆微孔复合织构，且沿圆周方向周期分布如图2所示，为便于计算，取1/N部分作为计算单元体，在建立织构化理论模型的基础上，利用数值模拟的方法系统考察织构参数，如：织构深度hp、织构面积率Sp、三角形微孔偏转角度α、椭圆微孔偏转角度β；操作参数，如：密封间隙h0、动环旋转速度n对密封性能参数的影响，如：承载力F、泄漏量Q、流体膜刚度K。

图2 动环表面配置的三角形-椭圆复合表面织构

利用Gambit软件完成三角形-椭圆复合微孔几何模型的网格划分如图3所示。设定计算单元体外径处为高压，内径处为低压，其余两边界施加周期边界。

图3 三角形-椭圆复合微孔几何模型的网格划分

设定密封流体不可压缩，且密度、黏度及密封腔内温度保持定值。利用Fluent软件可计算出端面的流场，进而获得承载力及泄漏量。计算过程中：首先，选择SIMPLIC算法以加速求解；其次，采用二阶迎风格式对控制方程进行离散；最后，利用 Fluent-Reports中的 “Forces”、“Fluxes”计算出所选单元体内承载力和泄漏量的大小。

1.2 数值计算

直角坐标系下流体的连续性方程为：

流体的局部膜厚为：

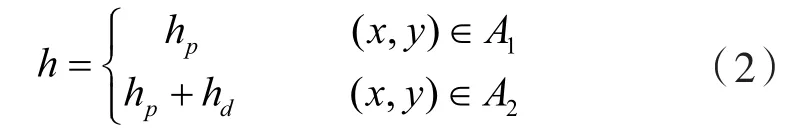
式中 hd——孔深；

A1，A2——无织构区域和有织构区域。

联立方程（1）（2），并在计算单元体边界处施加如下边界条件，即可计算出单元体区域内的流体压力分布。

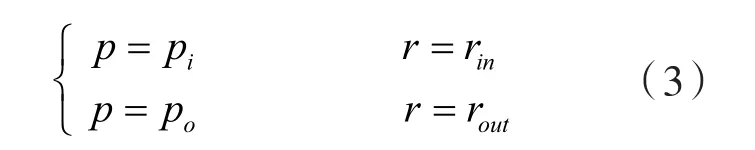
式中 pi，po——动静环入口、出口压力；

r ——流体质点到环心的局部半径。

周期性边界条件满足：

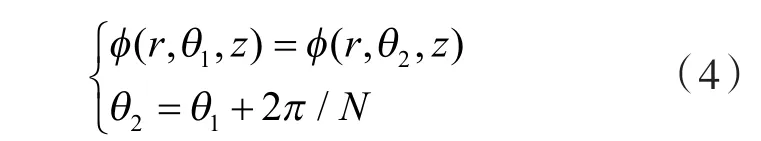
式中 θ1，θ2—— 计算单元体区域沿周向的起止和终止角度；

z ——直角坐标系下的竖坐标；

N——周期数。

泄漏量Q表示在单位时间内流过密封端面的流体总量，Q的大小直接反应了机械密封性能的优劣。膜刚度K定义为流体膜抵抗外部干扰的能力，即：在外界干扰的情况下，流体膜厚度发生细小变化所引起密封端面承载力变化的大小。

2 计算结果与分析

假设复合微孔织构的其他参数保持不变，设定进口压力为2个标准大气压，即pi=0.2 MPa，出口压力为1个标准大气压，即po=0.1 MPa，织构深度hp=4 μm，密封间隙h0=2 μm，织构面积率Sp=10%，动环转速n=5 000 r/min，三角形偏转角α=0°，椭圆微孔偏转角β=0°，考察某一参数变化对密封性能参数的影响规律。

2.1 密封端面的压力分布

本文选取参数如下：动环内径rin=15 mm、外径rout=20 mm，密封流体为液态水，其动力黏度η =1×10-3kg/（m·s），密度ρ=103kg/m3，温度T=25 ℃。通过FLUENT软件计算出3种不同类型织构化密封端面的流体动压分布，如图4所示。

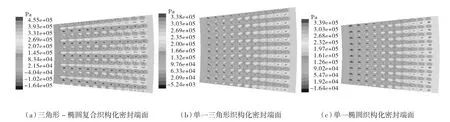
图4 不同类型织构化密封端面的流体动压分布

由图4可知：（1）由于“收敛楔”效应，密封端面的流体动压沿线速度方向收敛，端面压力急剧上升；（2）由于“气穴效应”的影响，在每个微孔发散域内产生流体负压，最终密封端面将产生了额外的承载压力。

选取3种不同类型织构化端面的任意一截平面，获得其截平面上的压力分布曲线，如图5所示。

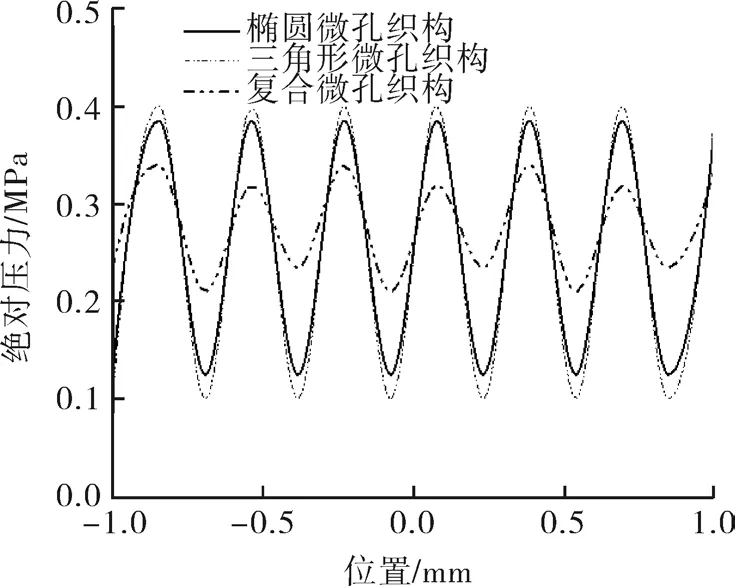
图5 微孔织构截平面内的压力分布

由图可以看出：在截平面内，三角形-椭圆复合织构化的流体最大动压小于2种单一类型织构，但三角形-椭圆复合织构化的流体最小动压却大于单一微孔表面织构。该结果是由于在密封端面同时配置三角形、椭圆微孔织构，彼此间存在“协同效应”，复合织构将部分压力峰值“补给”空化部分，进而减小“楔形效应”的影响。

2.2 织构深度hp对密封性能参数的影响

图6示出了不同类型织构化密封端面的承载力F、泄漏量Q以及流体膜刚度K随织构深度hp的变化关系曲线。由图分析可知：伴随hp的不断增大，3种不同类型织构化密封端面的F值均先迅速增大后缓慢减小，且在相同的hp条件下，三角形-椭圆复合织构化端面的承载力F要大于其他2种单一类型织构化密封端面。随着hp的增加，泄漏量Q呈现先减小后增大的变化趋势。这是由于当hp增大时，流体介质流动的截面积也增大，复合微孔织构的泄漏量Q小于其他两种单一微孔织构，且3种不同类型的织构的最佳织构深度都为2 μm。流体膜刚度K随着hp值得增大呈现先增大后减小的变化规律。当hp＞5.5 μm或hp≤4 μm时，三角形-椭圆复合微孔织构化密封端面的流体膜刚度要优于其他2种单一类型织构。

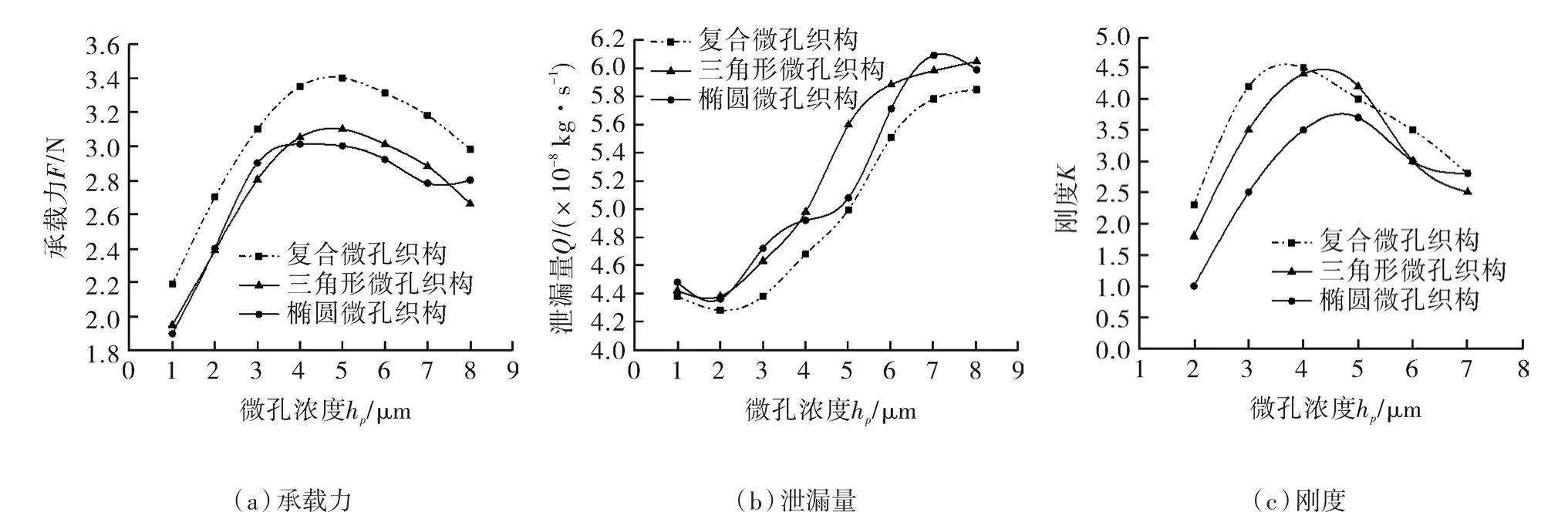
图6 织构深度hp对密封性能参数的影响

2.3 密封间隙h0对密封性能参数的影响

单一三角形、单一椭圆及三角形-椭圆复合织构化密封端面性能参数随密封间隙h0的变化规律如图7所示。由图可知，当密封间隙 h0在 1～8 μm 之间逐渐增大时，3种类型密封端面的承载力均先增大后减小；且小间隙（h0=2 μm）有利于密封端面承载力F的提升；在相同的h0条件下，三角形-椭圆复合织构类型端面的承载力F大于其他2种单一织构类型。泄漏量Q随着h0的增大而不断增加，但在相同的h0下，三角形-椭圆复合织构类型端面的泄漏量小于2种单一织构类型。当h0＜4 μm时，三角形-椭圆复合织构类型端面的流体膜刚度则比单一织构端面的流体膜刚度要大，而当h0＞4 μm时，膜刚度受h0的影响极小。

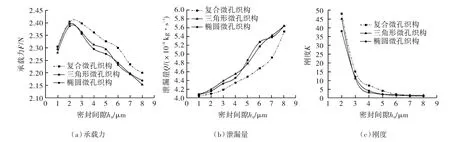
图7 密封间隙h0对密封性能参数的影响

2.4 织构面积率Sp对密封性能参数的影响

图8示出了织构化端面密封性能参数随织构面积率Sp的变化关系。由图可知：随着面积率Sp的增大，3种织构的承载力F都呈增大的趋势；在相同的Sp下，复合微孔织构具有更好的承载能力。泄漏量Q随Sp的增大呈现出波动式上升，当Sp≤10%时，不同类型织构化端面的泄漏量Q均较小，但当Sp＞10%时，3种织构化端面的泄漏量Q剧增。伴随Sp的增大，三角形微孔、三角形-椭圆复合微孔端面的膜刚度K也逐渐增大，椭圆微孔端面的刚度K则先增大后减小。这可能是由于椭圆微孔边界较平滑，随着面积率的增大，流体在进入椭圆微孔时会有更多的流体浸满孔内导致膜厚增加，从而刚度较小。

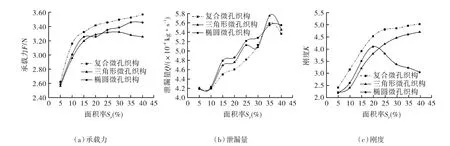
图8 织构面积率Sp对密封性能参数的影响

2.5 动环旋转速度n对密封性能参数的影响

动环旋转转速n对不同类型织构化端面密封性能参数影响如图9所示。

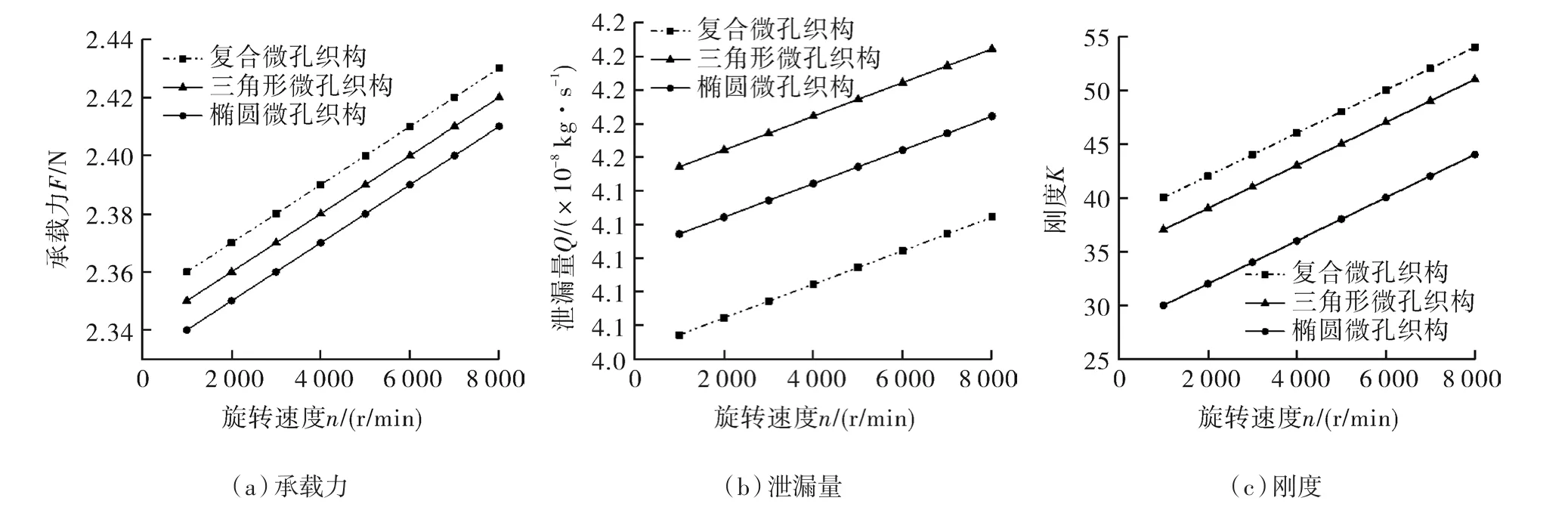
图9 旋转速度速n对密封性能参数的影响

由图可以看出，一方面，伴随转速n的不断增大，所有密封端面的承载力F、泄漏Q、流体膜刚度K均呈现线性增大的趋势。这是由于随着转速的提高，动压效应明显增强，承载及刚度提升，但与此同时，压力梯度将导致端面的泄漏加剧。另一方面，对比3种类型织构化端面，随着n的增大，三角形-椭圆复合微孔织构化端面的承载能力线性增加，但其泄漏Q的增加量缺相当微小，由此可以得出，在密封端面配置本文所提出的三角形-椭圆复合织构类型，不仅能够促使密封端面承载能力的有效提升，同时还有利于控制端面的流体泄漏。

2.6 偏转角α，β对密封性能参数的影响

本文选取的偏转角α，β值为 0° - 60°，其对3种类型织构化端面密封性能参数的影响如图10所示。伴随椭圆微孔偏转角β的不断增大，承载力F呈现M形变化规律、泄漏量Q呈现余弦形变化规律、刚度K呈现波浪形变化规律，且在α =15°，β =10°～20°时，3种织构化端面均达到自身的最佳密封性能，即：较大的承载和流体膜刚度，且泄漏量较小。对于不同类型的织构化密封端面，当α =15°，β=10°～20°时，三角形 - 椭圆复合微孔织构化密封端面具备最佳的综合密封性能。

图10 偏转角α，β对密封性能参数的影响

以上数值计算的结果及各密封性能参数的变化规律与文献［23-25］中基本一致，即验证了该模型和方法的合理性。

3 结论

（1）伴随织构深度hp的增大，承载力F、刚度K呈现先增大后减小的变化规律，而泄漏量Q则先减小后增大。

（2）当密封间隙h0＜4 μm时，三角形-椭圆复合微孔织构化端面的承载力F、泄漏量Q、流体膜刚度K均优于其他两种单一微孔织构化端面。

（3）三角形、椭圆微孔的偏转角度α，β对3种不同类型织构化端面密封性能具有显著影响，当α =15°、β=10°～20°时，三角形 - 椭圆复合微孔织构化密封端面具有最佳的综合密封性能。