基于分数阶傅里叶变换的运动脑电信号分类方法

黄小爽

(惠州开放大学,广东 惠州 516000)

0 引 言

脑电信号(Electro Encephalogram Gram, EEG)作为一种产生机理非常复杂的非平稳、非线性随机信号，负责传递大脑对人体的控制信息[1-3]。通常大脑对肢体的控制过程可以表述为：大脑产生特定的思维活动，通过中枢神经系统传递给脑外周神经系统，脑外周神经系统去控制肌肉系统映射到四肢的运动。但是对于患有运动障碍的患者，由于神经组织病变等原因不能将EEG传递给肌肉，无法进行相应的动作。针对该类患者，Vidal于1973年第一次提出了脑机接口(Brain Computer Interface, BCI)技术的研究成果。BCI作为一种新型的人机交互方式，直接利用计算机等外部设备对EEG进行采集，进而采用模式识别方法对EEG提取特征和分类识别，从而将EEG与特定的运动(例如举起右手)联系起来，达到不经过大脑外周神经和肌肉系统等传统大脑输出回路也能向外界传输信息的目的[4-6]。

特征提取和模式分类是决定模式识别方法是否有效的关键技术，他们相互配合又相互制约，共同决定着BCI技术的使用效果，是BCI技术的难点也是国内外学者研究的热点。当前主要的脑电信号特征提取方法有傅里叶变换法(Fast Fourier Transform, FFT)、短时傅里叶变换法(Short Time Fourier Transform, STFT)、功率谱法、AR模型法、独立主分量法、小波变换法和经验模态分解法(Empirical Mode Decomposition, EMD)等。其中FFT作为一种全局变换，脑电信号频域特征的提取是以损失时域信息为代价的，该方法不适用于非线性、非平稳的脑电信号分类[2]；STFT方法虽然具备时-频域联合分析能力，但是其时间分辨率和频率分辨率是相对矛盾的，因此分析脑电信号时有一定的局限性[7]；功率谱法与FFT方法类似，都损失了脑电信号的时域信息[8-9]；AR模型法能够反映脑电信号的时变特征，但是AR模型参数估计精度受脑电信号数据长度影响，当数据长度较小时，参数估计精度较差[10-11]；独立主分量法作为一种多通道分析方法，能够对脑电信号中的重要节律成的分进行增强，该方法的代价是多个通道增加了系统的复杂度和成本，限制了其在工程实际中的推广应用[12]；小波方法[13-18]和EMD方法[19-20]是近年来被广泛应用于非平稳、非线性信号处理中的多尺度、自适应信号处理方法，然而小波方法对信号的分解是基于基函数实现的，并且需要预先设置分解层数，基函数的选择和分解层数的设置对信号分析和分类性能影响较大，目前还没有一种普适的基函数选择和分解层数设置方法；EMD方法能够自适应地将信号分解为一系列本征模函数(Intrinsic Mode Function, IMF)和的形式，相对于小波方法不需要预先设置基函数和分解层数，但是“边缘效应”的存在影响着EMD方法的使用。在模式分类方面，当前常用的方法有线性分类器、神经网络分类器、贝叶斯分类器、支持向量机(Support Vector Machine, SVM)和相关向量机等，其中SVM在面对小样本、非线性及高维模式分类问题时相对于其他几种分类器具有更强的鲁棒性、更高的分类性能和计算效率，因此在脑电信号分类中获得了广泛应用。

本文在上述研究的基础上，针对运动脑电信号非平稳、非线性的特点，提出一种基于分数阶傅里叶变换(Fractional Fourier Transform, FrFT)[21]的运动脑电信号分类方法，首先利用不同阶次的FrFT对脑电信号进行分析，将特征提取维度扩展到分数域，然后在分数域提取反映不同运动差异信息的2维特征，最后利用SVM分类器[22]进行分类，基于实测数据的实验结果表明所提方法能够获得92.57%的分类结果，明显高于传统FFT方法和小波方法，为脑电信号模式分类提供了新的手段。

1 实验数据介绍

本文实验所用数据采用与文献[4,9-10]一致的奥地利格拉兹技术大学(Graz University of Technology)公开的BCI数据中DataⅢ数据集，该数据集也是BCI2003国际竞赛所用标准数据集。实验数据的采集对象为25岁女性，实验中所执行的意识任务是受试对象根据屏幕指示想象左、右手运动，并利用符合国际标准的EEG放大器对受试对象的脑电信号进行采集。一次实验过程的持续时间为9 s，流程如图1所示。受试者最初处于放松状态，观察前方显示屏，然后根据显示屏的指示想象左右手运动：

1)在0 s≤T<2 s时，受试者前方显示屏处于黑屏状态，受试者安静放松。

2)在T=2 s时，显示屏亮起并出现“+”光标，提示受试者开始实验。

3)在3 s≤T<9 s时，显示屏随机出现“←”或“→”箭头提示受试者根据光标想象左手或者右手运动。

实验过程中数据的采样频率为128 Hz，并利用带通滤波器滤除0.5 Hz～30 Hz外的无用信号，一次实验在9 s时间内能够采集1152个样本点，其中有效数据为第3 s～第9 s之间的768个样本点。数据集中包含C3和C4这2个通道的数据，共280组。

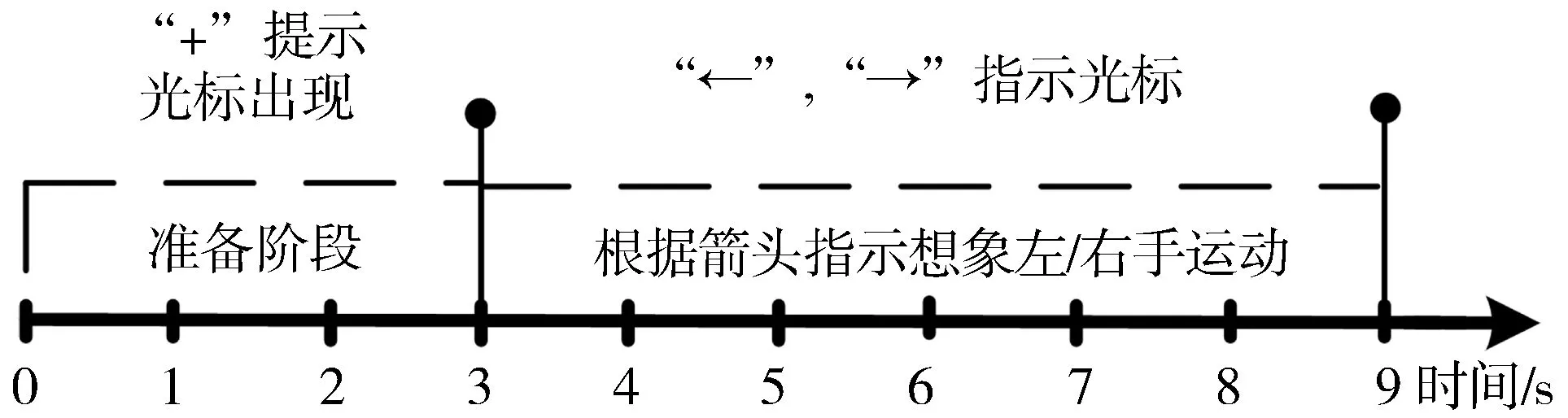
图1 一次实验的数据采集时序

2 分数阶傅里叶变换

傅里叶变换(Fourier Transform, FT)自1807年提出以来迅速成为信号分析与处理领域使用最为广泛的一种数学工具，在科学理论研究和工程实际应用中都发挥着极其重要的作用，被当作经典信号处理理论的基础。但是随着对自然界探索的深入以及对信息科学理论研究的加深，除了平稳信号外，非平稳、非线性信号同样广泛存在于自然界，此时FT的局限性也逐渐暴露，作为一种全局变换，FT只能将信号在时域和频域之间进行整体转换，无法反映信号的局部特征。针对这一问题，FT被不断改进发展，出现了一系列新的信号分析方法，例如加窗傅里叶变换、Gabor变换、Wigner-Ville分布、Cohen类时频分布以及FrFT等，其中FrFT作为对传统傅里叶变换的一种推广，能够同时对信号的时域和频域信息进行处理，相对于传统傅里叶变换更适用于处理非平稳、非线性信号。

图2在时频平面形象地描述了FrFT与传统FT之间的关系，图2中横坐标为时间t，纵坐标为频率ω。当逆时针旋转角度α=0时对应的曲线为原始时域信号f(t)，当时域信号沿逆时针旋转α=π/2时得到信号的频谱f(ω)，这种变换即为传统傅里叶变换。而FrFT可以认为是将时域信号沿逆时针旋转任意α角度得到分数谱f(u)的过程，当α从0变化到π/2的过程中，FrFT展示了信号从时域逐渐向频域的变化过程，因此相对于FT只能在单一域(时域或频域)对信号进行分析的局限性，FrFT可以在不同分数域同时对信号进行分析和处理，从而可以扩展后续信息提取维度。

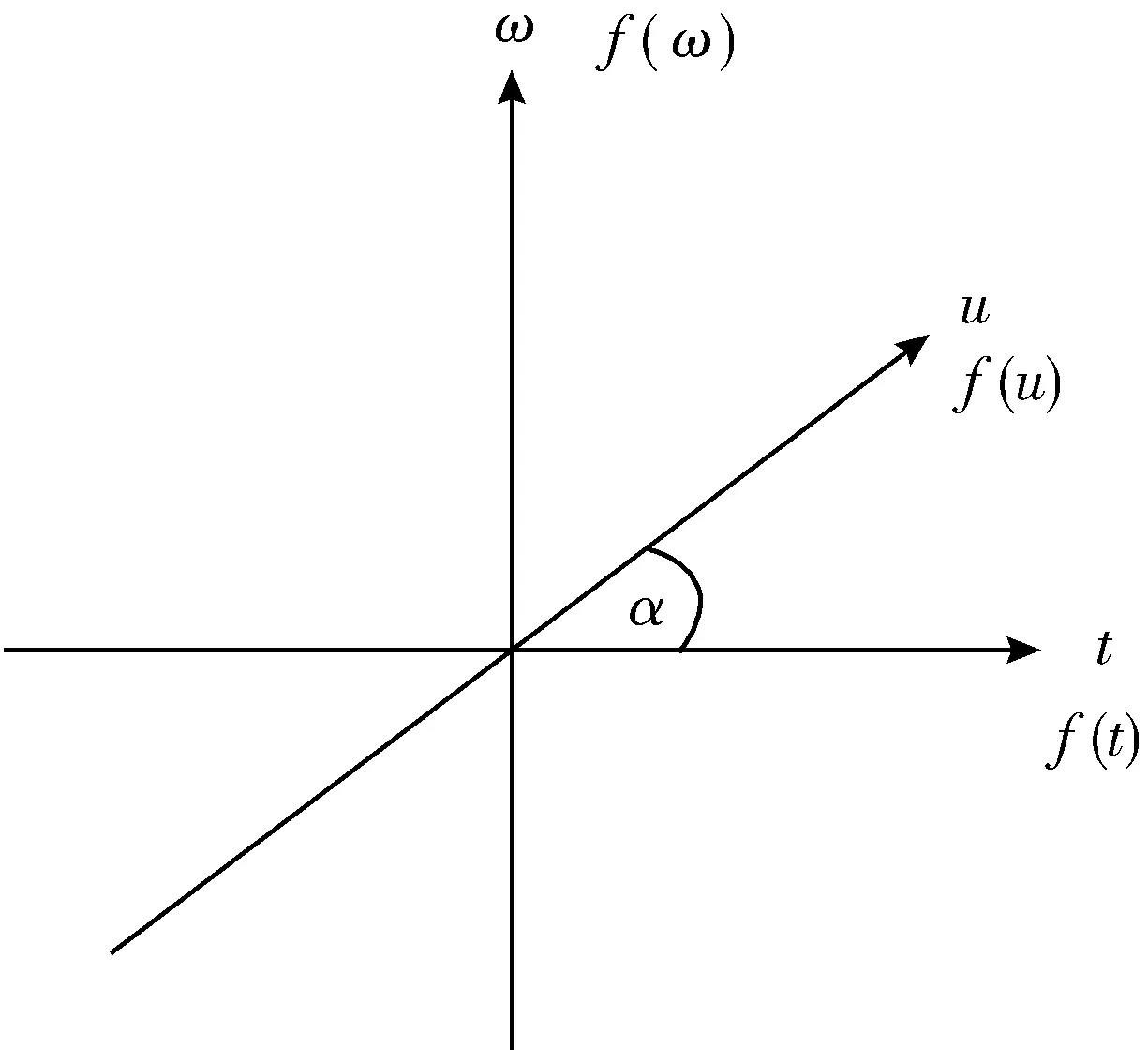
图2 FrFT与传统傅里叶变换关系示意图

对于给定时域信号f(t)，其p阶FrFT可以表示为：

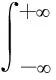
(1)

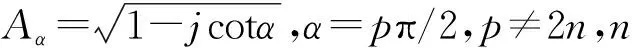
由于实际工程使用中都是针对离散信号进行处理和分析，因此需要将式(1)进行离散化得到离散分数阶傅里叶变换(Discrete Fractional Fourier Transform, DFrFT)。目前使用最广泛的是Ozaktas采样型离散方法，该方法首先对原始信号进行时域展开，然后根据香农定理对信号进行插值计算，最后得到FrFT的离散化处理结果，即对式(1)按式(2)进行展开：

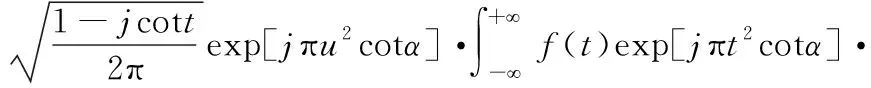
exp[-j2πutcscα]dt

(2)

然后根据香农定理，对f(t)exp[jπt2cotα]进行插值计算可得：

f(t)exp[jπt2cotα]

(3)

最后将式(3)代入式(2)即可得到原始信号f(t)的p阶DFrFT为：

(4)

其中，n和m分别表示对信号时域和分数域的采样点，N为时域信号采样总点数，时域采样间隔为1/Δx。

根据上述分析，对于任意给定信号，通过设置不同的阶次p，根据式(4)可以计算得到对应的fp(m)，对于脑电信号分类而言，虽然不同阶次的fp(m)可以扩展特征提取的维度，但是维度的增加反过来也会加大分类识别算法的运算量和复杂度，因此如何寻找最优的FrFT阶次p，从而在分类性能和计算复杂度之间得到平衡变得非常关键。本文采取相关系数最小的方法来确定最优阶次p，即对于给定脑电信号f(t)，首先计算其不同阶次p=0,0.1,…,1时FrFT得到对应的fp(m)，然后计算想象左手运动fp(m)和对应想象右手运动fp(m)的相关系数，相关系数最低的fp(m)则表明其包含的想象左手运动和想象右手运动的信息差异最大，适合用来进行分类。

图3(a)给出了对想象左手运动和想象右手运动的C3通道实测数据进行不同阶次时FrFT得到的相关系数，可以看出相关系数最小的为0.9阶，即认为0.9阶FrFT中包含的差异性信息最多，能够用来进行分类。图3(b)给出了对想象左手运动和想象右手运动的C4通道实测数据进行不同阶次时FrFT得到的相关系数，可以看出相关系数最小的为0.4，同样认为0.4阶FrFT中包含的差异信息最大，能够用来进行分类。图4(a)和图4(b)分别给出了C3通道实测数据进行0.9阶FrFT的分解结果和C4通道实测数据进行0.4阶FrFT的分解结果，可以看出，对C3通道实测数据进行0.9阶FrFT分解后，想象左手运动的支撑区宽度要明显小于想象右手运动的支撑区宽度，而对C4通道实测数据进行0.4阶FrFT分解后，想象左手运动的信号幅度从左到右有一个明显的上升趋势，而想象右手运动的信号幅度从左到右则呈现出相反的下降趋势。因此可以从0.9阶和0.4阶的分解结果中提取特征，对不同脑电信号进行分类。

(a) C3通道

(b) C4通道

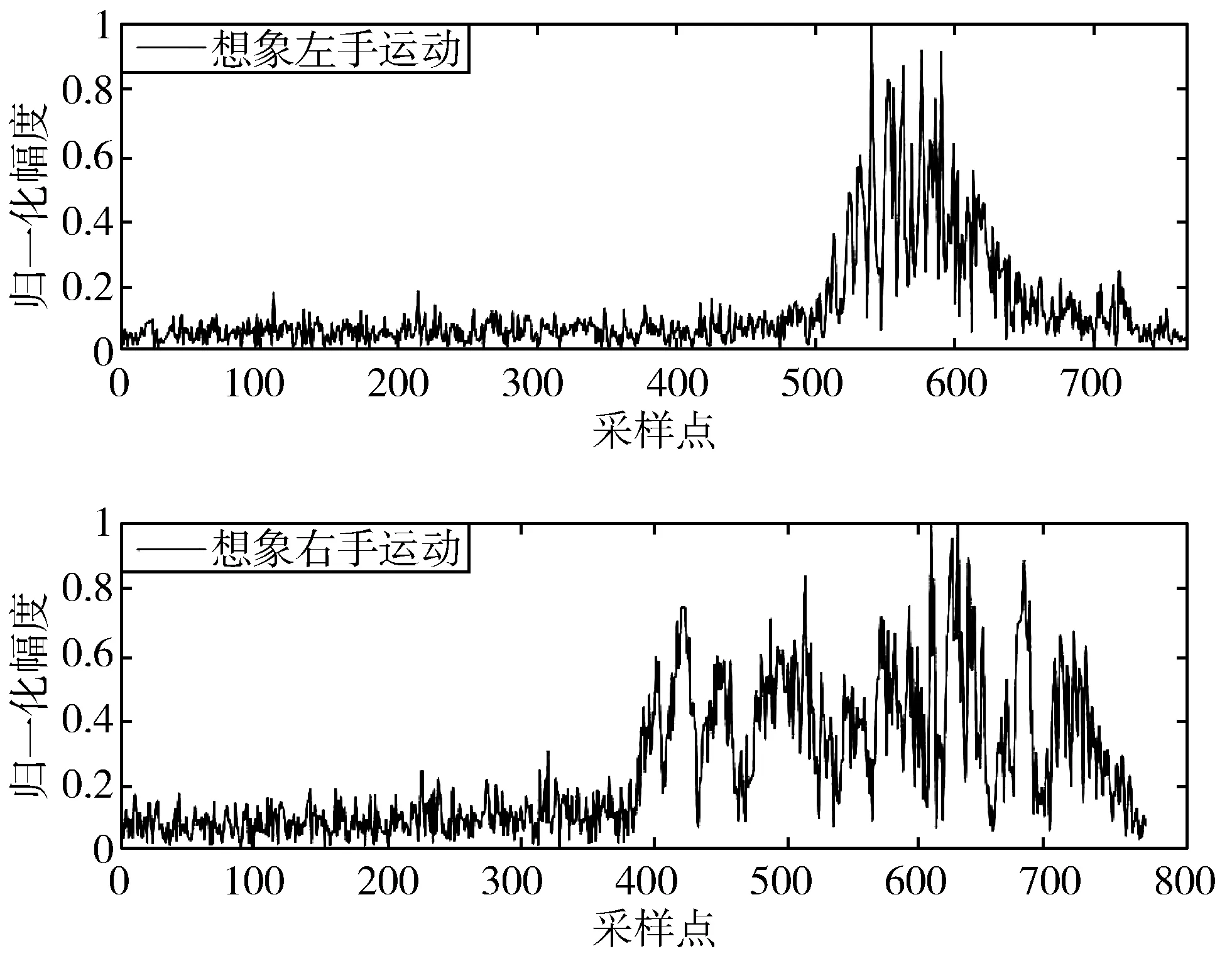
(a) C3通道0.9阶FrFT分解结果

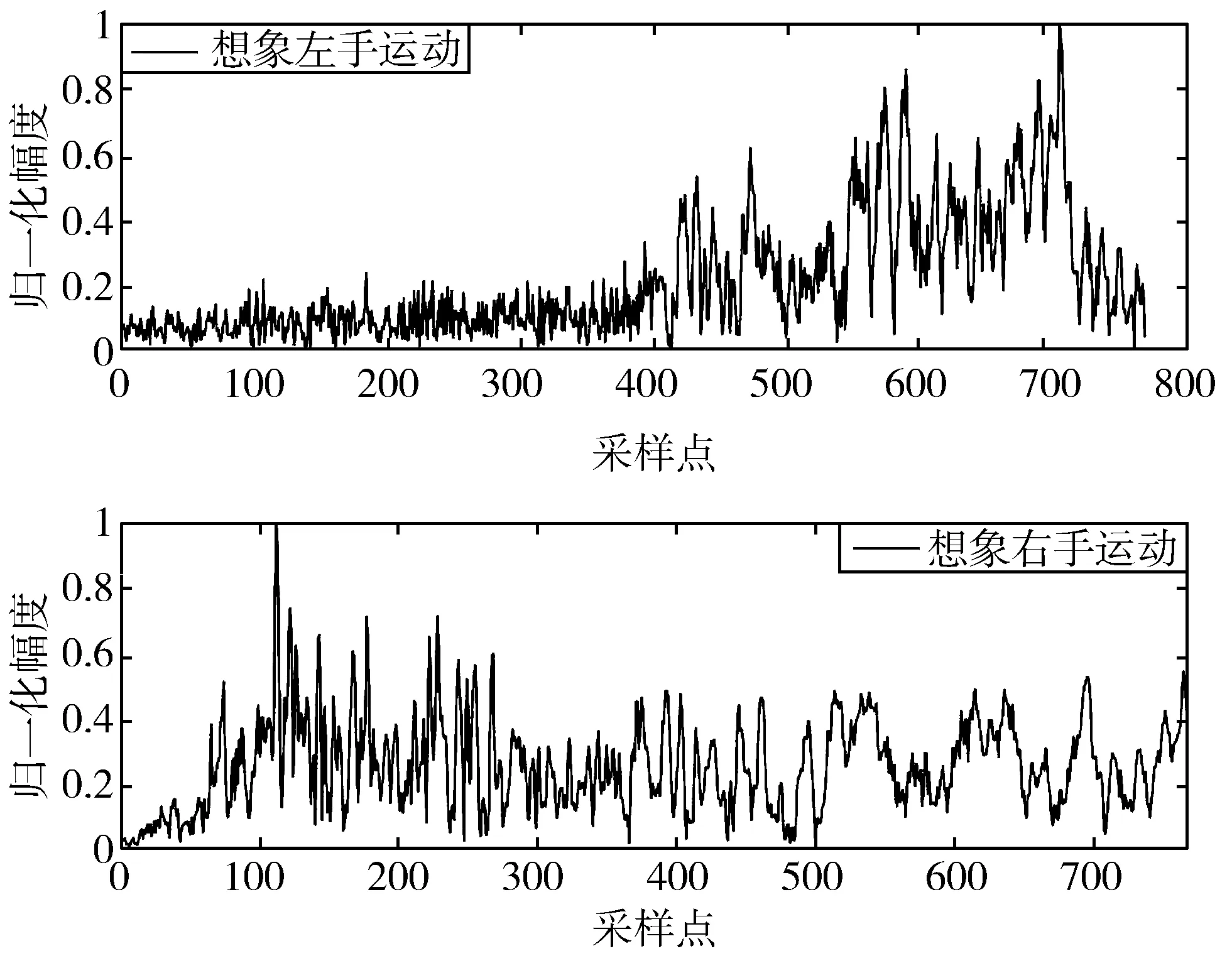
(b) C4通道0.4阶FrFT分解结果

3 特征提取和分类识别

3.1 特征提取

根据上述分析，提取如下2维特征进行分类：

特征1C3通道0.9阶FrFT信号的支撑区宽度特征：

Feature1p=0.9=

(5)

其中，find(·)表示计算满足括号中条件的样本点数。

特征2C4通道0.4阶FrFT信号的梯度和特征：

(6)

图5给出了对第2章介绍的脑电信号C3和C4通道实测数据提取上述2维特征得到的归一化特征值分布图，其中“o”为对想象左手运动脑电信号提取的特征值，“+”为对想象右手运动脑电信号提取的特征值，从图5所示结果可以看出，在特征域，2种运动脑电信号具有较高的可分性，能够用于后续目标分类。

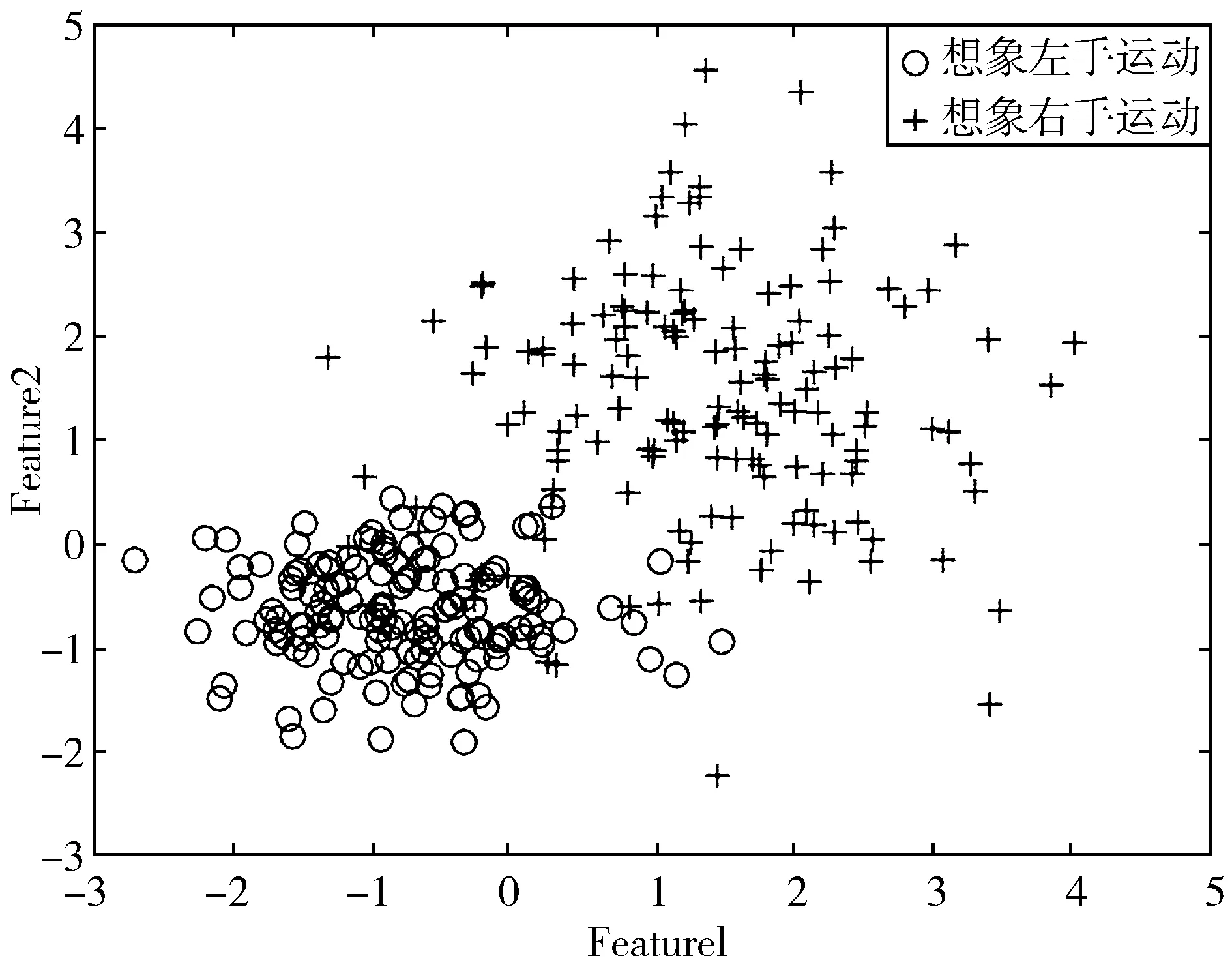
图5 2维特征归一化分布图

3.2 分类识别

在分类识别阶段，对280组实测数据进行划分，一半(140组)作为训练样本(其中70组为想象左手运动数据，70组为想象右手运动数据)，剩余140组作为测试样本(其中70组为想象左手运动数据，70组为想象右手运动数据)。在训练阶段，对训练样本提取上述2维特征构成特征向量，并利用该特征向量对SVM分类器进行训练，得到最优分类面(SVM分类器选用高斯核，利用交叉验证的方式确定核函数的参数为1.6)。在测试阶段，对测试样本同样提取上述2维特征构成特征向量，进而利用训练好的最优分类面对其进行分类识别。

表1给出了所提方法的分类结果混淆矩阵，混淆矩阵中每一类分类结果的计算方法为该类别中正确分类的样本数除以该类别的总测试样本数(70)，总的正确分类结果的计算方法为2类样本中正确分类的样本数和除以总的测试样本数(140)。将所提方法与FFT方法和小波方法进行对比，其中FFT方法为直接对信号进行传统傅里叶变化后提取与FrFT方法相同的2维特征进行分类，分类器选用SVM，小波方法为文献[12]介绍的利用小波包能量熵特征进行分类，并采用基于马氏距离的线性分类器对特征进行分类。从表1可以看出，本文所提的FrFT方法能够得到92.57%的正确分类结果，远高于传统FFT方法(84.63%)和小波方法(86.28%)。同时对于每种运动脑电信号，本文所提的方法均可以获得最优的正确分类性能。究其原因在于传统FFT作为FrFT的一种特征形式，直接将信号整体转换到频域，而从图3和图4所示数据相关系数的结果可以看出，当阶次为1时(频谱)，想象左手运动信号与想象右手运动信号的相关性较大，因此可分性较差，而小波方法同样采用的是小波域的单一特征，相对于所提的FrFT方法，小波方法信息提取的维度较为局限，导致其分类性能较低。图6给出了小波方法和传统FFT方法所提特征在2维特征上的归一化分布图，对比图6和图5可以看出，在特征域本文所提的FrFT方法特征可分性要明显优于小波方法和FFT方法提取的特征，与表1所示结果一致。

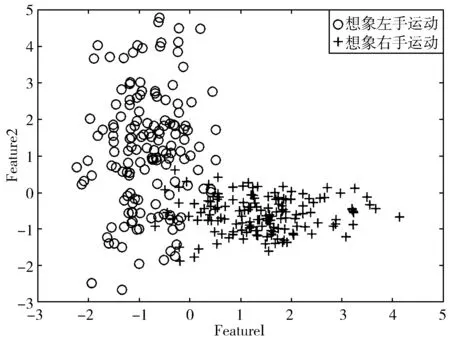
(a) 小波方法

(b) FFT方法

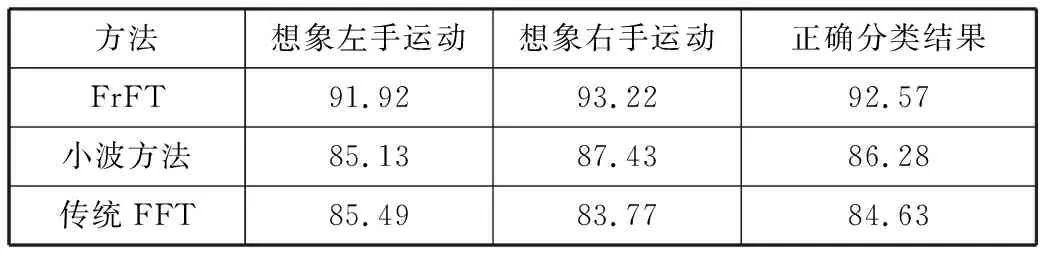
表1 不同方法分类结果混淆矩阵 单位:%

在实际工程应用中，能够获取的训练样本数往往有限，这就要求分类方法能够对样本数具有一定的鲁棒性，即在小样本条件下依然能够获得较好的分类性能。在这一部分实验中，将训练样本数分别设置为40、60、80、100、120、140(其中一半为想象左手运动数据，一半为想象右手运动数据)，对应的测试样本分别为240、220、200、180、160、140。图7给出了不同训练样本条件下不同方法的分类性能，可以看出随着训练样本数的增加，3种方法的分类性能都出现了不同程度的提升，但是本文所提FrFT方法在不同训练样本数的条件下都能获得最优的分类性能，并且在训练样本数较少时(少于80)，优势更加明显。同时当训练样本数超过80时，本文所提FrFT方法的分类性能已趋于稳定，表明FrFT方法在小样本情况下的鲁棒性更好，更适用于实际工程应用场景。

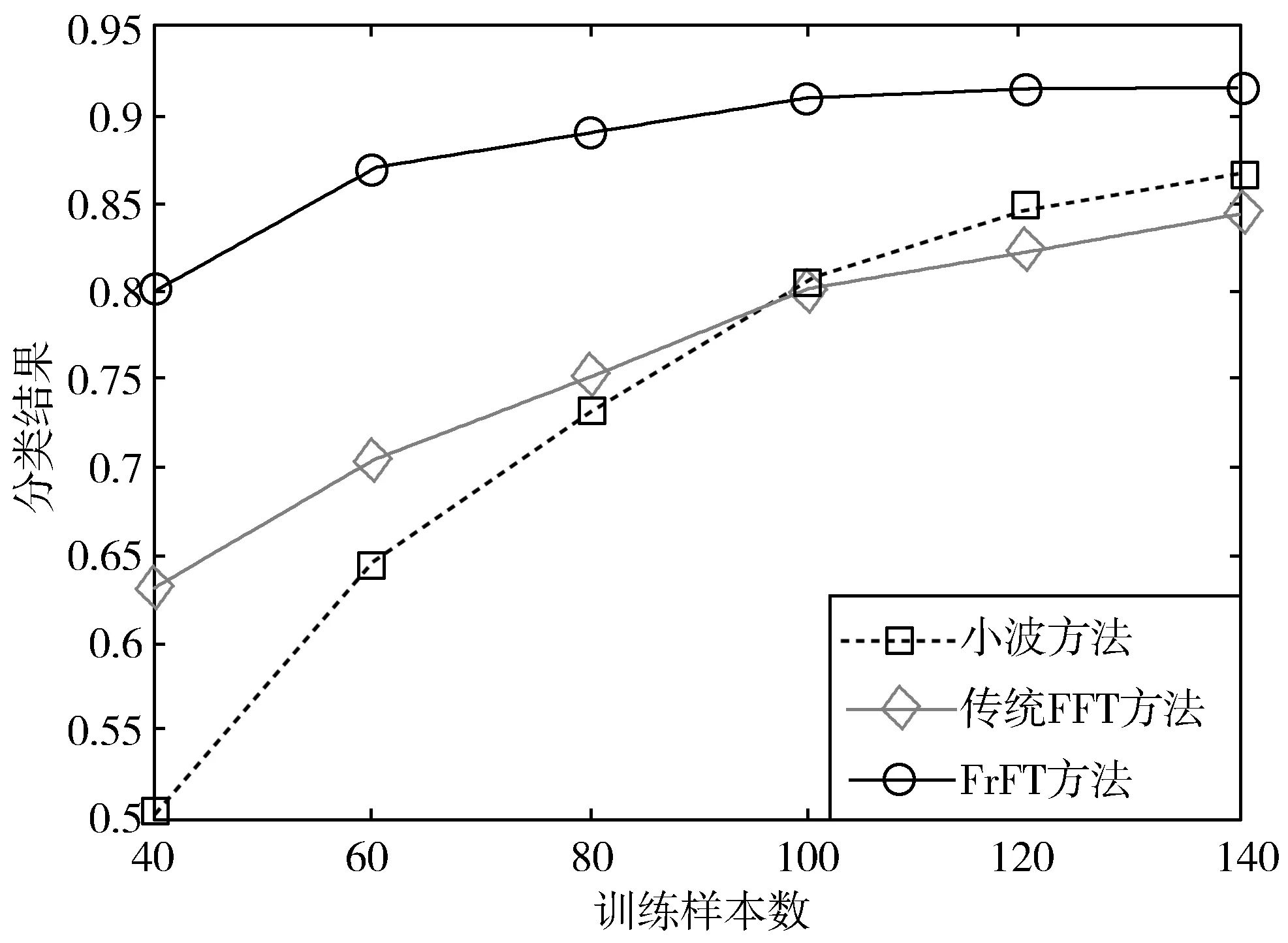
图7 分类结果随训练样本数的变化曲线

为了进一步评估本文所提方法在不同数据集下的有效性，采用与文献[12]一致的数据划分方式进行实验，在这种情况下文献[12]给出的小波方法得到的正确分类结果为90%，而本文所提方法经过计算可以得到93.6%的正确分类性能，明显优于小波方法，与前述分析一致。

4 结束语

特征提取和分类识别是当前脑机接口技术研究的难点与热点，脑电信号非线性、非平稳性的特点导致采用传统单一维度特征提取方法很难获得满意的分类性能。针对该问题，本文提出了一种基于FrFT和SVM的运动想象脑电信号分类方法，利用FrFT对时域信号进行分析，将其转换至不同阶次的分数域，从而实现特征域的扩展，然后根据相关性最小准则确定最优的分解阶次，并对最优阶次分解结果提取2维特征，最后利用SVM分类器进行分类。采用实测数据的实验结果表明本文所提方法可以获得优于传统方法的分类性能。同时设计实验对小样本条件下本文所提方法的分类鲁棒性进行验证，结果表明当样本数减少50%时，本文所提方法依旧可以获得较好的分类性能，适用于实际工程应用。