社交网络中正影响支配集问题的轮转贪心算法

万 科

(华南师范大学计算机学院,广东 广州 510631)

0 引 言

随着时代的发展，包括社交网络在内的各种各样的复杂网络逐渐兴起，人们也越来越关注和研究这种类型的网络。如果将复杂网络建模成图，图中点代表对象，图中的点与点之间的关系代表着网络中对象之间的联系。那么对复杂网络的研究就变成了对图的研究。近年来,支配集问题由于其在现实世界中的广泛应用而受到了关注[1-3]。随之而来也有一系列支配集的变体，例如连通支配集、符号支配集、k-重支配集等，这些概念也被广泛应用于优化理论、通讯网络的设计与分析、社会科学、计算复杂性和算法设计等许多领域[3-4]。

最近，有关支配集的一种新的变体被提出来，即正影响支配集(Positive Influence Dominating Set, PIDS)[5-6]。通过找到社交网络的正影响支配集就可以通过该集合对这个网络起到一个积极的影响。例如想在一个社区推广某种产品，如果对社区的每一个用户逐一进行推荐，就会非常费时费力。但可以针对网络中一小群有影响力的用户，选定这些用户可以在市场上产生最大的影响力覆盖范围，先向他们推荐让其接受这项产品，然后通过他们就可以影响到整个社区。当然，要达到时间最短、代价更小，就必须使有影响力的用户更少，即图中的正影响支配集的点数更小。点数最小的正影响支配集叫最小正影响支配集(MPIDS)。求解最小正影响支配集已被证明是一个NP难问题[7-9]。

对于NP难度问题，不太可能有多项式时间的精确求解算法。因此，从实用性角度看通常采用启发式算法近似求解，其中最简单的启发式算法是各种贪心类算法。贪心算法的基本思想是基于贪心势函数作出判断和选择依次形成一个可行解向量作为贪心解输出。其优点是简单、快速，但由于贪心势函数是基于局部信息，因此形成的贪心解易过早陷入局部最优，往往不尽人意。有一些策略可以增强贪心算法所得解的质量，典型的增强策略包括Pilot方法、后悔贪心策略、迭代贪心策略和轮转贪心策略等[10-17]。

Pilot方法是一种类似于博弈中向前看的策略。其基本思想是基于贪心势函数选择解向量X的当前第i分量值xi时，穷尽xi所有可能的情况，针对每一种可能情况向前继续用贪心算法试探求出最终结果，其中导致最好结果的xi将作为解向量X的第i分量值。该方法产生的解理论上要好于原贪心算法解，但其时间代价较大[10]。

迭代贪心策略的基本思想是针对贪心算法获得的贪心解，先随机撤销(Deconstruction)若干分量，然后对剩余的部分解向量用贪心算法进行重构(Reconstruction)。这2个阶段的过程(即撤消、重构)可进行多次迭代，最终将最好的结果输出[11-12]。

后悔贪心策略的基本思想是，在贪心算法基于贪心势函数逐次形成贪心解向量的过程中，允许对之前作出的解向量的分量进行适量修改(比如，如果发现对之前的分量作更换结果会更好就更换之前的分量)。对于集合覆盖问题已从理论上证明了允许后悔的贪心算法比原贪心算法具有更好的近似性能。在后悔贪心算法最近应用于无线传感器网络中干扰最小化问题上，实验研究表明该算法可明显提高现有贪心算法的精度[13]。

最近提出的轮转贪心策略的基本思想是，先用贪心算法形成贪心解向量，保留前面一定比例的连续个解分量(即部分解向量)，然后依次对这个部分解向量去掉最前面的1个分量，并随后用贪心算法补构1个分量。这个过程可以反复多次。最后连续执行贪心法直至形成一个可行解作为最终输出结果。对于点覆盖、集合覆盖、MLST、随机森林等问题，轮转贪心算法可以在一定程度上提高贪心解的质量且增加的计算时间较小[14-17]。

相较而言，这些增强策略中轮转贪心策略在时间复杂度方面有明显的优势，能保持时间复杂度几乎不变的前提下有效增强贪心解的质量。

关于最小正影响支配集问题，目前文献中有2个典型的贪心算法，即Greedy-by-Wang和Greedy-by-Raei，根据来自不同视角的贪心势函数反复添加最佳的节点进入正影响支配集。这2个算法在不同的数据集上各有一定的优势。本文将轮转策略结合求解正影响支配集问题的2个贪心算法进行结合，提出求解最小正影响支配集的相应的轮转贪心算法，并通过实验表明新算法比现有贪心算法所获得解的质量有一定程度上的提高，且增加的计算时间也在可接受范围内。

1 问题描述和相关算法

1.1 问题描述

社交网络可用图来表示，因此社交网络的正影响支配集问题可通过图的相关概念来描述。给定无向图G=，其中V是节点集，E是边集。对于任意点vV，用N(v)表示v的相邻点的集合，即N(v)={uV|(v,u)E}；d(v)=|N(v)|为节点v的度。度为0的点称为孤立点。本文考虑的图都是无孤立点的无向图。

定义1给定无向图G=，如果图G的一个点集DV满足对于任意的vV，N(v)中至少有d(v)/2个点属于D，则称D为图G的一个正影响支配集。图G中点数最少的正影响支配集为图G的最小正影响支配集。

为了便于描述正影响支配集的贪心算法，下面引入几个概念。

定义2给定无向图G=V,E，假设D为贪心算法当前选中的支配点集，对于任意点vV，定义其满足度为相邻点中为支配点的个数与其度的一半之差，记作Sat(v)，即：

Sat(v)=|DN(v)|-d(v)/2

对于图中任意点vV，如果满足度Sat(v)0，则称点v为已满足点，否则称为未满足点。显然，如果图中所有点均是已满足点，则D为图的一个正影响支配集。

定义3给定无向图G=V,E，假设D为贪心算法当前选中的支配点集，对于任意非支配点vV-D，定义其覆盖面为邻域N(v)中未满足点的个数，记作Cov(v)，即：

Cov(v)=|uN(v)|Sat(v)<0|

定义4给定无向图G=V,E，假设D为贪心算法当前选中的支配点集，对于任意非支配点vV-D，定义其期盼度为邻域N(v)中未满足点的满足度绝对值之和，记作Exp(v)，即：

Exp(v)=uN(v)Sat(u)<0|Sat(u)|

1.2 相关算法

求解最小正支配集问题有2个典型的贪心算法，它们基于不同的视角采用不同的贪心势函数来依次选取最佳节点加入到当前支配点集中，直到支配点集成为一个正影响支配集。其中一个贪心算法的贪心势函数是基于覆盖面Cov(·)[18]，本文称作算法Greedy-by-Wang，另一个贪心算法的贪心势函数是基于期盼度Exp(·)[19]，本文称作算法Greedy-by-Raei。

算法Greedy-by-Wang的思想比较直观自然，基本思路是先将图中全部点初始化为非支配点和未满足点，选取一个当前覆盖面Cov(·)最大的点加入正影响支配集中，然后更新每个点的覆盖面。重复此步骤直到图中所有节点都为已满足点为止。算法Greedy-by-Raei的基本思想是先将图中全部点初始化为非支配点和未满足点，选取一个当前期盼度Exp(·)最大的点加入到正影响支配集中，然后更新每个点的期盼度。重复此步骤，直到图中所有节点都为已满足点为止。这2个算法的时间复杂度均为O(n3)，其中n=|V|。实验研究表明，与算法Greedy-by-Wang相比，算法Greedy-by-Raei通常求得的解的质量有一定优势，但在一些平均度比较大的实例图中效果较差[20-21]。

鉴于算法Greedy-by-Wang和算法Greedy-by-Raei各有优势，将这两者进行融合得到一种混合贪心算法Hybrid-Greedy，其基本思想是在执行贪心算法Greedy-by-Wang的过程中，如果当前覆盖面Cov(·)取最大值的点有多个，则选择其期盼度最大点作为支配点。算法Hybrid-Greedy的时间复杂度仍为O(n3)，但其实际运行时间约等于参与融合的这2种贪心算法的运行时间之和。实验研究表明，Hybrid-Greedy能融合2种贪心算法的优势，在大多数测试算例中所得解的质量有明显提高[21]。

2 轮转贪心算法

2.1 轮转贪心策略

贪心算法通常都是基于选定的贪心势函数依次构建出贪心解向量的每个分量。在这个过程中，每一步都要根据贪心势函数做出贪心选择。尽管这种贪心选择都是基于局部信息的，但在形成贪心解向量的早期，由于依赖的信息少，比较盲目，而在后期因为贪心解向量的前面很多分量已经选定，会使得此时做出的贪心选择往往比较精准。基于这一洞察，贪心解向量的前面分量的构造对最终获得好的贪心解向量非常关键[14]。

轮转贪心策略旨在通过精心构造好一个贪心解向量的前面部分来最终获得一个高质量的贪心解，它由3个阶段组成。第1阶段，根据贪心算法构造出一个贪心解向量S=(v1,v2,…,vk,…,vt)。第2阶段，先将该向量尾部β|S|个分量舍弃后获得当前的部分解向量R=(v1,v2,…,vk)，然后对该当前部分解向量迭代如下操作α|S|次：去掉头部(即当前解最前面)的1个分量，并使用贪心算法构造出1个分量放在尾部(即当前解最后面)。第3阶段，根据迭代后获得的部分解向量R，继续使用贪心算法构造出一个完整的可行解R作为轮转算法的最终结果。轮转贪心策略的直观示意图见图1。

图1 轮转贪心策略示意图(假设|S|=t,α=1,β=(tk)/t)

该策略中需要指定参数α和β，其中α用于控制轮转次数，β是要舍弃贪心解向量的百分比。实际应用中可根据期望获得解的质量和运行时间来合理选择。

2.2 轮转贪心算法

基于前述讨论，轮转贪心算法是在基本贪心算法产生了完整的贪心解向量(可视作队列结构)之后，再以该解向量的前面部分为出发点，多次轮转进行删除、插入操作。下面以算法Greedy-by-Wang为基本贪心算法，描述对应的轮转贪心算法，具体实现过程见算法1。

算法1Caro-Greedy-by-Wang

Input:无向图G=V,E,参数α和β

Output:G的一个正影响支配集

Begin

1.由算法Greedy-by-Wang产生解向量S

2.RS中去掉后面β|S|个分量

3.Fori=1 Toα|S| Do

4.删除R中排在最前的1个分量

5.用算法Greedy-by-Wang在R后添加1个分量

6.End For

7.用算法Greedy-by-Wang在R后依次添加分量直到R为一可行解

8.ReturnR

End

根据算法1易知，如果将基本贪心算法换为算法Greedy-by-Raei，则得到其相应的轮转贪心算法，记作Caro-Greedy-by-Raei。

下面以上述算法为例来分析轮转贪心算法的时间复杂度。设图G中点数为n=|V|，贪心算法Greedy-by-Wang用时间t(n)求得贪心解向量S。求得贪心解向量S的每个分量的平均时间为t(n)/|S|。从中容易看出，Caro-Greedy-by-Wang运行中总共做了添加解向量分量的操作次数为|S|+α|S|+β|S|=(1+α+β)|S|<(2+α)|S|，故总时间不超过(2+α)t(n)。由于α通常是一个很小的常数，故Caro-Greedy-by-Wang的时间复杂度与算法Greedy-by-Wang相同，均为t(n)，而其实际运行时间不超过算法Greedy-by-Wang实际运行时间的一个常数倍，即(2+α)倍。由此可见，轮转贪心算法的时间复杂度与其基本的贪心算法相同。

轮转贪心算法除了开始需要运行贪心算法得到贪心解作为出发点，之后只产生问题的唯一一个完整可行解并输出。这一点与其他增强型贪心算法不同，比如迭代贪心、Pilot贪心等。也正是这一点导致轮转贪心算法的时间复杂度与其基本贪心算法相同，并成为轮转贪心算法相比其他增强型贪心算法的一大优势。

3 实验结果及分析

3.1 实验方法和实验数据

本节通过实验来评估轮转贪心算法的性能，包括实际运行时间和解的质量。实验中将2种轮转贪心算法Caro-Greedy-by-Wang和Caro-Greedy-by-Raei分别与其基本贪心算法(算法Greedy-by-Wang和算法Greedy-by-Raei)作比较。此外，还将2种轮转贪心算法与吸收2种基本贪心算法优势的混合贪心算法Hybrid-Greedy做比较。所采用的数据是社交网络中的真实实例，包括来自斯坦福大学的大型网络数据集(http://snap.stanford.edu/data/)中的7个无向图类型的社交网络实例(前7个算例)，以及2个著名社交网络实例(其中ncstrlwg2是科研合作网，数据来自文献[22]，actors-data是演员合作网，数据来自文献[23])。由于本文要求图中没有孤立点，因此需要对算例做预处理，移去孤立点或将孤立点随机连接到某个其他节点来确保图中存在正影响支配集。表1给出了这些测试算例的描述。

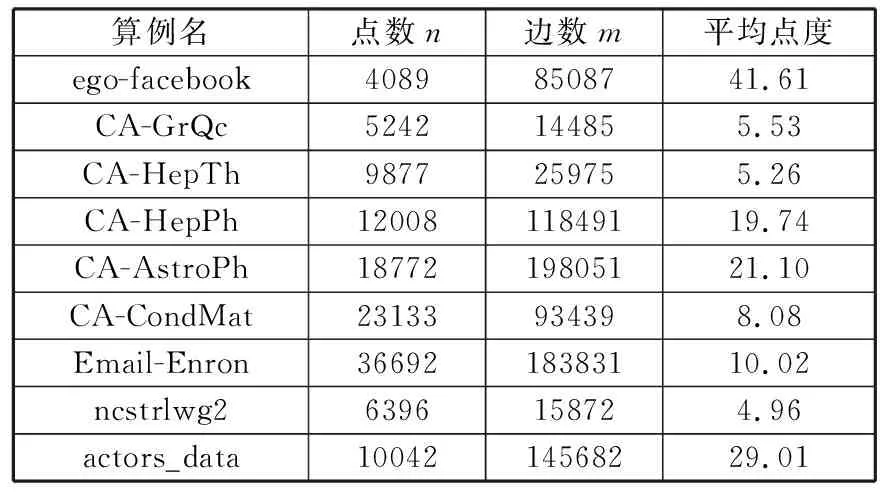
表1 测试算例描述

3.2 实验结果及分析

算法用C语言编程实现，实验环境为：PC机处理器为i7-7700，主频为3.60 GHz，内存为8 GB和64位的Win10操作系统。

首先本文测试了轮转算法中的2个参数α与β的不同取值对轮转贪心算法解质量的影响。表2中是在算例CA-HepPh上轮转贪心算法Caro-Greedy-by-Wang对α与β取不同值的实验结果，其中α分别取值为1、2、3、4、5、6，β分别取值为5%、10%、15%、20%。表2中的数字代表最小正影响支配集包含点的个数，数字越小说明点的个数越少，解的质量越高。

表2 Caro-Greedy-by-Wang中参数α、β取不同值时在算例CA-HepPh上的实验结果

算例CA-HepPh用算法Greedy-By-Wang的实验结果是4892，而从表2可看出Caro-Greedy-by-Wang在α较小时，随着α与β的增大，解质量有提高；当α=4,β=15%时达到峰值，之后解质量就慢慢下降。

基于表2的结果，在随后的实验中，对2种轮转贪心算法中α取值分别为1、2、3、4、5、6，β取值分别为5%、10%、15%、20%时进行了实验，然后取平均值，实验结果见表3～表5。表中的PIDS代表求到的最小正支配集的点数，Time代表运行的时间。

从表3和表4可以看出，Caro-Greedy-by-Wang相比算法Greedy-by-Wang，Caro-Greedy-by-Raei相比算法Greedy-by-Raei，所求的最小正支配集的点数更少，解的质量上均有不同程度的提高，而增加的计算时间在可接受范围内，这说明轮转贪心算法能够克服基本贪心算法执行早期中贪心选择的一些盲目性。

从表5可以看出，轮转贪心算法与混合贪心算法相比，解质量也有一定程度上的提高，而运行时间差别并不是很大，在可接受的范围内。这进一步说明了，轮转贪心策略在一定程度上能纠正基本贪心算法执行早期所作出的一些错误选择。

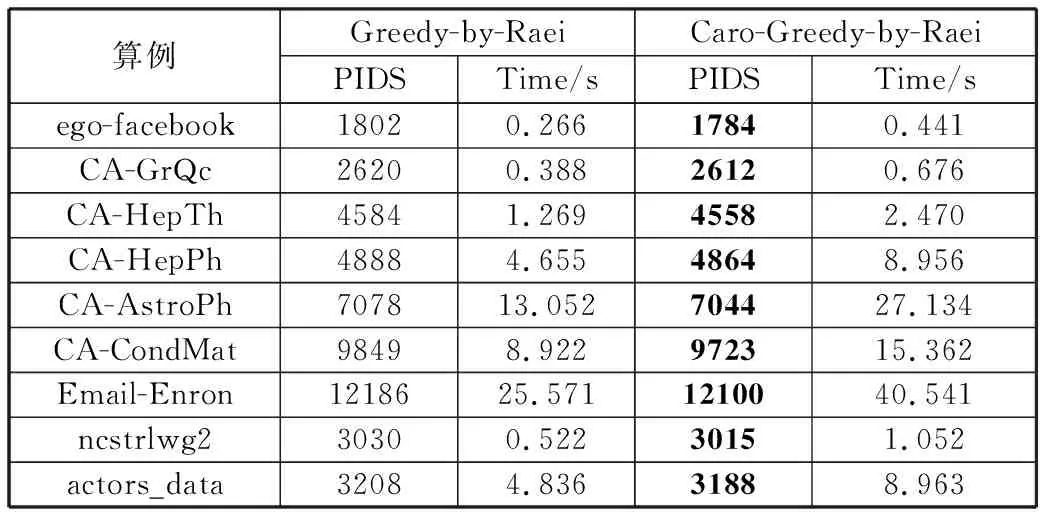
表3 算法Greedy-by-Raei与Caro-Greedy-by-Raei在各测试算例上的实验结果

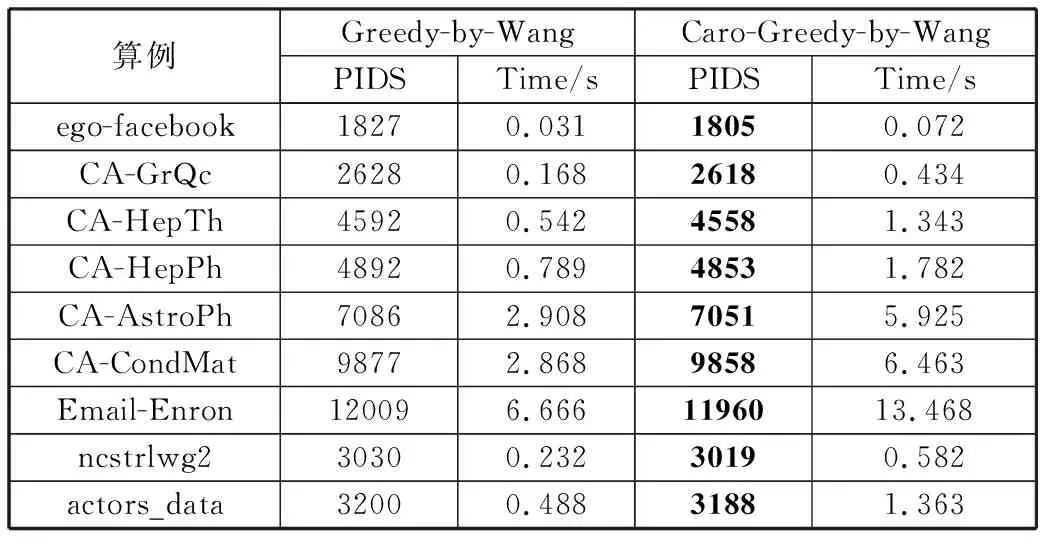
表4 算法Greedy-by-Wang与Caro-Greedy-by-Wang在各测试算例上的实验结果

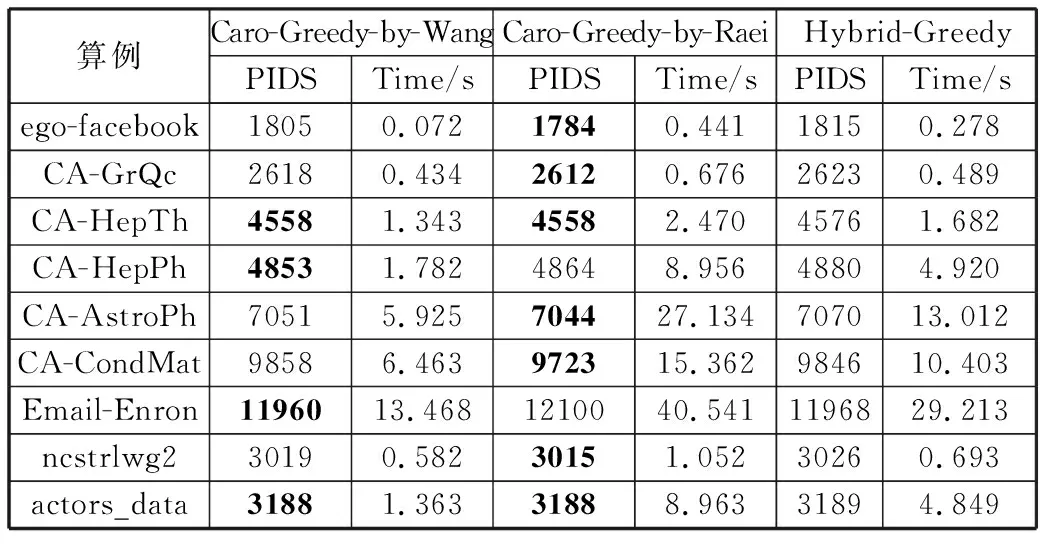
表5 轮转贪心算法与Hybrid-Greedy的实验结果

4 结束语

在求最小正支配集问题中，本文基于现有的2个贪心算法，结合轮转贪心策略，分别提出了相应的轮转贪心算法。与原贪心算法比较，轮转贪心算法可在一定程度上提高解的质量且增加的计算时间较小。

未来工作中将通过广泛实验探究轮转贪心算法的机理，并探究轮转贪心算法如何与其他启发式算法进行融合来求解社交网络中包括最小正影响支配集问题在内的各种典型问题。