不同雪荷载分布形式下弦支穹顶结构稳定性研究

王 猛，王军林，李红梅，敦晨阳，孙建恒

（河北农业大学 城乡建设学院，河北 保定 071001）

弦支网壳形式最早是由日本政法大学的川口卫（M. Kawagucki）教授于1993 年提出的，他将单层网壳结构和索穹顶结构部分组合起来，组成现在所定义的弦支网壳［1］。弦支网壳结构将索与杆形成整体，索的预应力通过撑杆传力，使得上部单层网壳产生1 个向上的位移，与荷载作用下产生的位移相抵消。相对索穹顶，弦支网壳结构减小了周围环梁的压力，降低了施工难度。

随着工程上不断的应用，在静力的稳定方面［2-3］、地震方面的动力响应［4-5］、风荷载方面［6-7］和冲击荷载方面［8］都有相对较多的研究成果。但是，全球气候条件在近些年有很大的恶略发展趋势，各种建筑都会受到严重的影响。其中，风雪的作用最为关键。又由于以往分析中，大跨结构受到其中的影响更为突出，相对弦支穹顶在此方面的研究也比较少。由于雪荷载在分布形式上具有不均匀性，荷载位置的复杂性会造成结构的失稳，而弦支穹顶和一般意义的网壳结构在这种情况下有明显区别。因此，进行非均匀分布雪荷载作用下弦支穹顶结构的稳定性分析、找出与传统单层网壳结构的区别、判断失稳时的雪荷载分布情况，可为弦支网壳结构设计分析提供理论依据。

1 弦支网壳分析模型及参数选取

如图1（a）所示，凯威特型球面网壳跨度40 m，矢跨比1/8，即矢高5 m。其中，网壳杆截面分别为 径向121 mm×3.5 mm，斜向114 mm×3.5 mm。拉 索和撑杆的布置如图1（b）所示，由外向内外撑杆长度为3、3、3、2、2 m，撑杆直径和尺寸均为90 mm×2.5 mm。经过对比分析，初始构型的准 则［10］和以撑杆控制截面法确定预应力最优［11］，环索预应力值由内向外依次设置为11、35.2、55、102.3、177.1 kN。预应力的引入方法采用初始应变法，利用ANSYS 分析软件进行形态分析后根据式（1）确定初始应变。

式（1）中均为拉索相关的变量。ε 为应变；σ 为施加的预应力，单位：N/m2；E 为弹性模量，单位：N/m2。

分析中考虑结构的几何非线性和材料非线性。上部网壳杆件选用Beam188 梁单元，竖向撑杆采用Link8 单元，索采用只承受拉力的Link10 单元。材料采用钢材Q235，密度ρ=7 850 kg/m3。杆件屈服强度fb=235 MPa，拉索屈服强度fc=1 330 MPa。杆件和拉索的弹性模量，分别为E1=2.06×1011和 E2=1.8×1011，单位N/m2，泊松比v=0.3。

图1 结构构成图Fig.1 Cable-suspended dome

2 雪荷载分布形式

依据《建筑结构荷载规范》［12］，雪荷载标准值按式（2）选取，取1 kN/m2的雪压，积雪分布系数μr和μr,m按式（3）和式（4）计算。

式（2）中，Sk为雪荷载标准值，单位：kN/m2； μr为屋面积雪分布系数；S0为基本雪压，单位：kN/m2。 式（3）和式（4）中，μr为均匀积雪分布系数；μr,m为不均匀积雪分布系数；l 为跨度，f 为矢高。依据式（3）和式（4），计算求得：均布时μr=1；雪载较大分布时μr,m=1.45；雪载较小分布时μr=0.725。

图2 为积雪分布形式，其中阴影较深的区域为较大雪载分布，阴影较浅的区域为较小雪载分布，其它阴影区域为均匀雪载分布。文献［12］和文献［13］，雪荷载分布采取均布、非均布和全跨、半跨、最外两环半跨排列组合，得出6 种形式。

图2 雪荷载布置方式Fig.2 Snow load distribution mode

3 稳定承载力分析

根据图2 设置的6 种雪荷载分布情况，利用ANSYS 软件对K6 型弦支穹顶进行稳定承载力分析，分析结果见图3、图4 及表1；图5 为6 种不同雪荷载分布时网壳的失稳节点；图6（a）、图6（b）、图6（c）分别为全跨均布雪载变形图、半跨均布雪载变形图和半跨最外两环均布雪载变形图（变形放大5 倍）。

图3 均布雪载荷载—位移曲线Fig.3 Load-displacement curve of uniform snow load

图4 非均布雪载荷载—位移曲线Fig.4 Load-displacement curve of non-uniform snow load

表1 雪载作用下弦支网壳结构的稳定承载力Table 1 Stability bearing capacity of suspended-dome under the snow load

图5 失稳点位置Fig.5 Location of instability nodes

图6 结构变形图Fig.6 Structural deformation configuration

从图3 及图4 中可以看出，无论是均布雪荷载还是非均布雪荷载，雪荷载作用在半跨时网壳的稳定承载力最低。从表1 中可以看出在半跨雪荷载用下，半跨非均匀较大雪荷载对应的稳定承载力略低于半跨均布雪荷载对应的稳定承载力，是雪荷载的最不利分布形式，但两者相差不大。这与文献［12］及文献［13］中的半跨雪荷载作用在最外两环时网壳稳定承载力最低的结论不一致。

弦支网壳与单层网壳的不同点在于，弦支网壳的撑杆可以提高网壳的稳定承载力。如图6（a）及图6（b）所示，在全跨受载时，结构变形主要向荷载方向发展，变形对称，使得下部索的拉力增大，对结构起到有利作用，增加了稳定承载力；半跨作用时，荷载的不对称导致结构变形不对称，随着网壳荷载的加大，部分竖向撑杆倾斜导致与其连接的索的拉力减小甚至完全松弛，降低了稳定承载力。而在最外两环均布雪荷载作用下，结构稳定承载力相比全跨和半跨布置分别增加了106.2 %和142.6 %， 与之前文献［13］中单层网壳结构结论不一致。这是由于弦支穹顶的索拉力对结构稳定承载力起到重要影响作用。弦支穹顶最外两环布置的索预应力较大，相比第3 环环索，最外两环环索预应力增加了86% 和222% 。较大的预应力使得最外两环抵抗竖向荷载能力增强，使得网壳的最低稳定承载力由最外两环的半跨非均匀较大雪载布置形式变为整体半跨非均匀较大雪载布置形式，对应的结构失稳点也由文献［13］中的最外两环向网壳的中心点移动（图5、表1），增大了稳定承载力。另外从图3 和图4中可以看出弦支网壳失稳后的荷载位移曲线下降比相应的单层网壳要平缓，这表明弦支网壳的失稳较单层网壳失稳过程要平缓一些。

综上分析，半跨非均匀较大雪载布置形式对弦支穹顶结构稳定性最为不利，相比全跨均布雪载，稳定承载力下降15.5%；相比全跨非均匀雪载，稳定承载力下降了4.6%。

4 网壳失稳前后预应力索及撑杆应力变化过程分析

选取最不利的半跨非均匀较大雪载布置的荷载— 位移曲线，并在曲线上选取如图4 所示3 个荷载点A、B、C。如图7 所示，将失稳节点9 的弦支构件分为撑杆（单元350）、环索（单元439、440）、内环斜索（单元553、554）和外环斜索（单元566、567）。失稳节点对应的撑杆与索的荷载—应力变化曲线如图8 所示。

图7 失稳节点撑杆变形过程Fig.7 Deformation process of braces in instability node

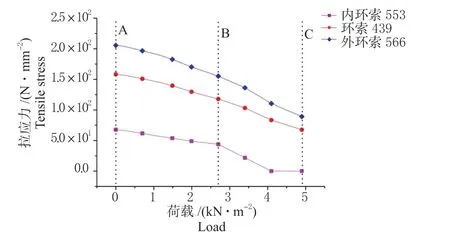
图8 撑杆和拉索荷载—应力曲线Fig.8 Load-stress curves of braces and cables

从图7 和图8 中可以看出，随着荷载的增加，撑杆及与其相连的预应力索的应力不断减小，当达到失稳点C 点时，撑杆、环索及外斜索的应力下降到加载初期的50%左右，而内环索的应力下降到完全松弛的零应力状态。对于撑杆，在加载初期（A 点）及失稳前（B 点），节点9 对应的撑杆一直是竖直的，但到达失稳点（C 点）时，由于预应力索的应力不断减小，撑杆由原来的竖直状态变为倾斜状态，此时撑杆对网壳向上的预应力变得越来越小，弦支网壳的位移迅速发展，最后结构失稳。

5 结论

（1）结构受半跨非均布较大雪载作用时，结构节点内收向结构里，拉索内力下降，从而承载力降低，导致此情况下结构的稳定最差。

（2）当非均布雪载布置在结构最外两环半跨时，结构稳定承载力最大。因为弦支网壳的结构特点，最外两环撑杆和拉索设置的预应力较大，使得最外两环可以很好地支撑竖向荷载，从而提高结构的稳定性。

（3）结构受载过程中，逐渐出现撑杆和拉索内力减小，而荷载的增大进一步加剧内力下降，并且失稳时，结构伴随着撑杆偏移竖直位置。