DTCWPT-TV 在高速列车齿轮箱轴承故障诊断中的应用

杨慧莹，伍川辉，李艳萍，龙 莹

（西南交通大学机械工程学院，四川 成都 610031）

1 引言

随着中国高速列车的快速发展，其安全性能受到了极大的重视。而齿轮箱轴承作为高速列车走行部中的关键部件，其状态与列车运行安全有着紧密的联系。列车实际运行中，轴承通常会承担着较大的运载负荷，加上制造、安装以及环境多方面的影响，其受到的各种机械应力，使得其状态发生改变，从而产生各种各样的缺陷[1]。一旦高速列车的齿轮箱轴承出现磨损、变形、胶合或者保持架损坏等现象，有可能对行车安全造成极大影响，产生严重的后果。因此，对高速列车齿轮箱轴承的故障诊断是非常必要且有意义的。

对于齿轮箱轴承振动信号这样的非平稳信号，传统的振动信号处理方法—傅里叶变换以及相关分析等都难以取得较好的效果。而小波变换作为现代振动信号处理方法中的一种，对非平稳信号具有很好的分析效果[2]。小波变换有很多优势，比如能够提取不同尺度的信号特征，具有多分辨率的时频特性。但是传统的小波分析由于隔点抽样会导致信息的丢失，并且存在平移敏感性、方向选择性差、混叠效应明显等问题，这使得其在微弱故障诊断和强噪声背景下的复合故障诊断中无法发挥作用[3-4]。针对这些不足，文献[5]提出了双树复小波变换（Dual Tree Complex Wavelet Transform，DTCWT），文献[6]又在此基础上进一步发展。DTCWT克服了传统小波变换的不足，具有良好的平移不变性、方向选择性和较小的频率混叠。为进一步提高信号高频部分的分辨率，双树复小波包变换（Dual Tree Complex Wavelet Package Transform，DTCWPT）被提出，从而减少信息的丢失。这使得DTCWPT 被广泛应用于滚动轴承、发动机、齿轮等的振动信号分析与故障诊断领域[4、7-8]。

由于高速列车运行中背景噪声较强，振动信号通过小波变换进行分解之后仍需要进行降噪处理。常用的小波阈值降噪会在信号的不连续处产生虚假的波峰和伪吉布森震荡，而奇异值分解（Singular Value Decomposition，SVD）去噪容易产生虚假分量，全变差去噪则不会出现这样的情况，因此采用全变差降噪以达到更好的效果[9]。全变差降噪的问题作为一个L1 正则化问题，可以通过优化极小化（Majorization-Minimization，MM）方法进行求解。经过验证，通过上述方法，可以有效地去除振动信号中的强背景噪声，较好地体现出冲击的故障特征。

2 双树复小波包变换

DTCWPT 由两个并行的离散小波包变换组成，其中，一个离散小波包变换被视为实部树，另一个被视为虚部树。在信号的分解和重构的过程中，保持虚部树的采样位置始终位于实部树的中间，这样在采样过程中就避免了信息的丢失，最后的结果就能够综合利用实部树和虚部树的信息[10]。因此，DTCWPT 具有近似平移不变性并且能够有效抑制频率混叠。

复小波基函数根据下式进行构造：

式中：ψr（t）—实部；ψi（t）—虚部。如果ψr（t）和ψi（t）构成一对希尔伯特变换对，则ψc（t）为解析信号。复尺度函数与复小波函数的构造方法相似。

DTCWPT 实部变换的小波系数dl（k）和尺度系数cJ（k）可以通过以下内积运算得到：

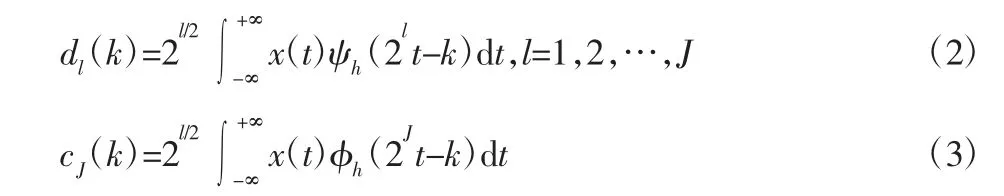
式中：l—尺度因子；J—分解层数；Ψh（t）—实部树的小波函数；Φh（t）—实部树的尺度函数。

同样，对于虚部树的小波变换的小波系数和尺度系数可以通过将式（2）、式（3）中的小波函数和尺度函数换成相应的虚部变换的小波函数和尺度函数。这样，通过两个实小波变换就可以实现DTCWPT 的分解。

3 稀疏追踪去噪

3.1 稀疏追踪去噪理论

一组冲击信号是具有稀疏特性的，其全变差很小；而如果这组冲击信号中混入噪声，信号相邻点间不平滑，随机变化较大，则其全变差就比较大。考虑到这一特点，通过将一组含噪声的冲击信号的全变差最小化进行稀疏追踪，则可以得到信号的稀疏表示。这样做的意义在于能够获得信号更为简洁的表达方式，也就是稀疏表示，实现消除噪声的目的，以便获取隐藏在信号中的有用信息[11]。

3.2 稀疏追踪去噪模型

通常，我们观测到含故障特征的信号可以用下式进行表示：

式中：y—观测到的含噪声的信号；x—被噪声淹没的故障特征；q—随机噪声。

要通过y 找到一个接近y 但全变差更小的x，求解的目标是全变差V（x）最小，但同时还要满足其误差E（x，y）在一定范围内。

n 阶全变差的定义以此类推。最小化一阶全变差时可能会产生阶梯锯齿，所以进行全变差优化时通常使用高阶全变差，这样可以使得优化后得到信号相对比较平滑。

但是，由于有约束的优化问题难以求解，因此可以将上述优化问题升维转化为无约束极值问题进行求解。引入一个拉格朗日乘子λ，将约束条件与原函数联系到一起，问题转化为求解下述方程[12]：

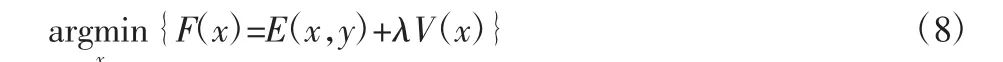
3.3 稀疏追踪算法

对于式（8），可以通过优化极小化方法进行快速求解[13]。对于函数h，可通过下述方程进行优化[14]：

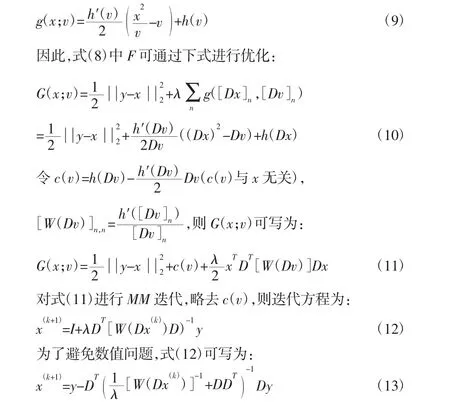
4 稀疏追踪与SVD 去噪对比

为了对全变差稀疏追踪方法在冲击特征提取上的有效性进行验证，现构造一组冲击仿真信号，其中，冲击单元为：

设定采样时间T=2s，采样频率f=1000Hz，采样点数N=2000。为了模拟强噪声环境，在冲击信号上加上方差为0.1 的随机噪声。信号添加噪声前后的的时域波形，如图1 所示。其对应的频谱，如图2 所示。采用全变差稀疏追踪的方法对含噪声信号进行处理，如图1（b）所示。设置参数λ=0.6，可以得到消除噪声后的信号，其时域波形与频谱，如图3 所示。

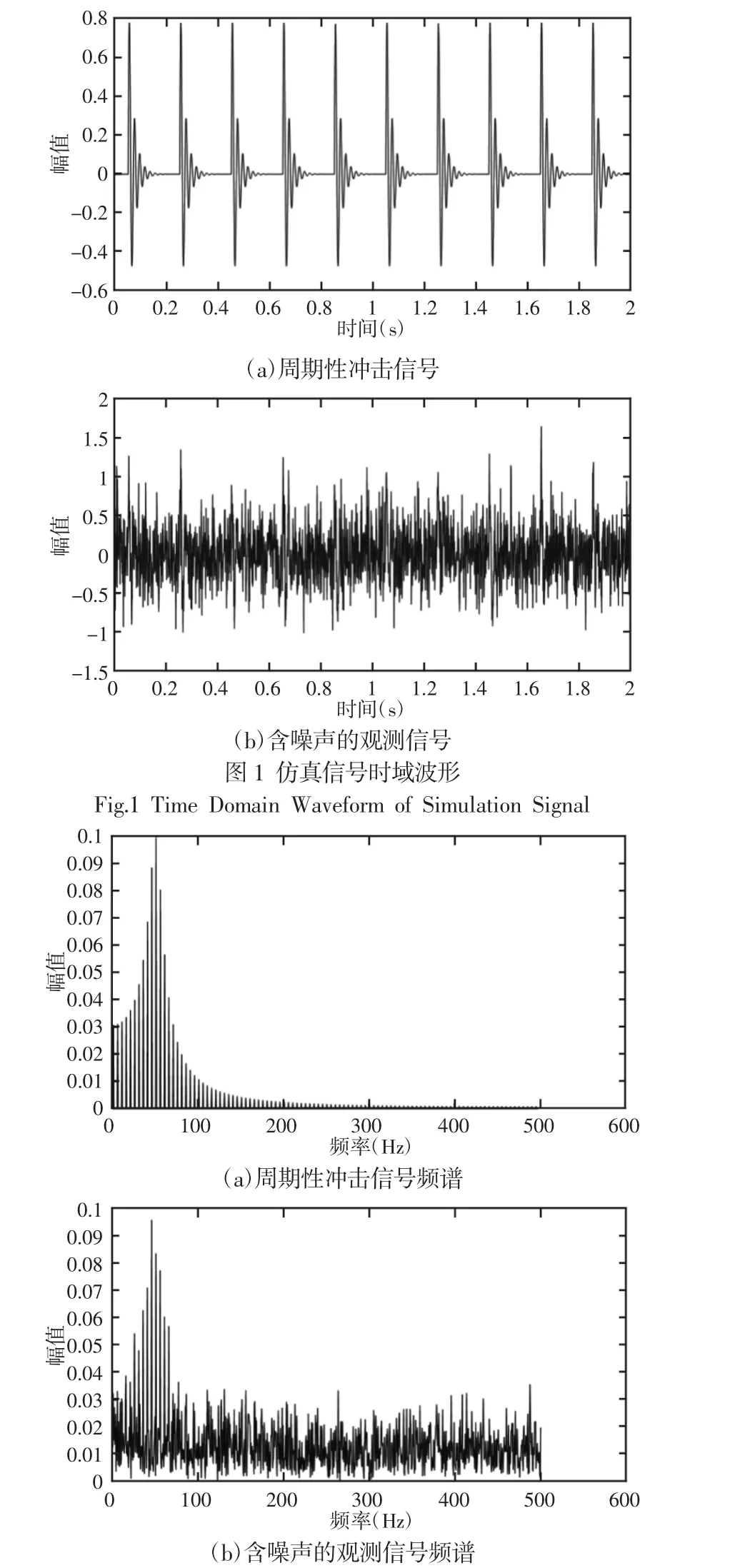
图2 仿真信号频谱Fig.2 Spectrum of Simulation Signal

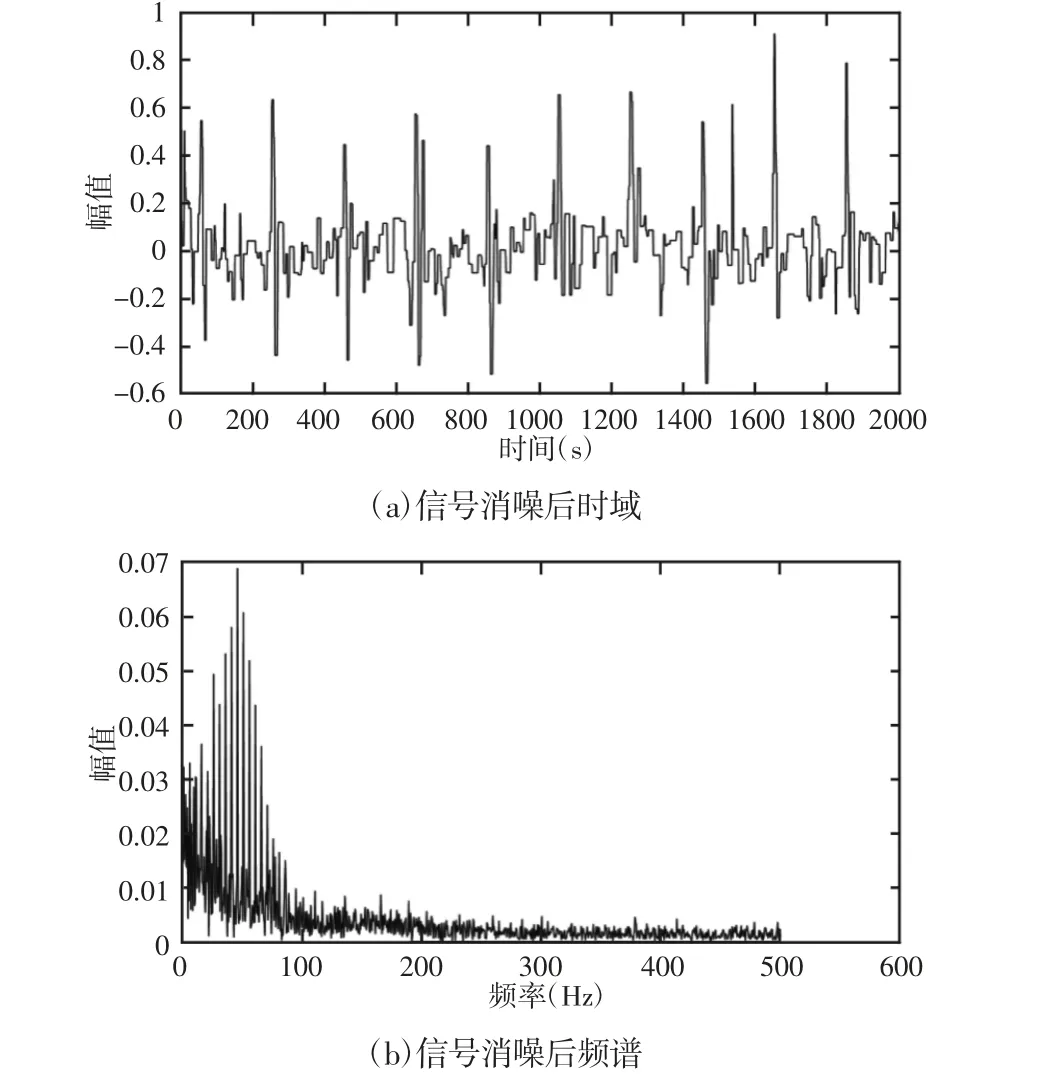
图3 全变差稀疏追踪方法消噪结果Fig.3 Noise Elimination Result by TV Sparse Tracking Method

对信号进行消噪的方法很多，其中SVD 使用得较为普遍[3、15]。但是SVD 方法存在很多问题，比如易产生虚假分量等。为了展现所用方法的优越性，对含噪声信号进行SVD 消噪处理，得到消除噪声后的信号，其时域波形与频谱，如图4 所示。

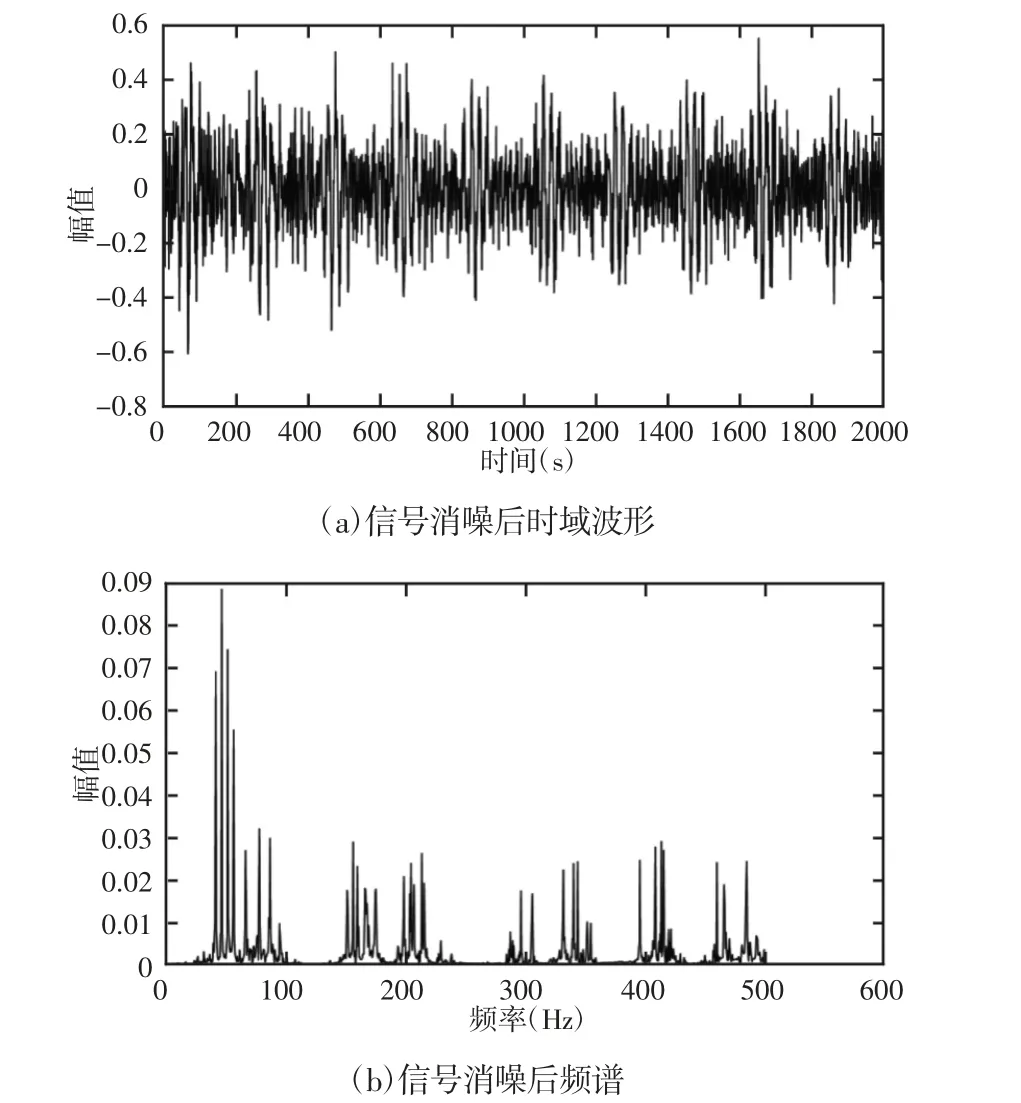
图4 SVD 消噪结果Fig.4 Noise Elimination Result by SVD

另外，将用两种方法消除噪声后的时域信号中的冲击截取出来，分别计算其峭度值结果，如图5 所示。对比上述两种方法，从以下几点可以看出全变差稀疏追踪方法比SVD 的消噪效果更好：从时域波形上来看，前者得到的结果冲击明显，且幅值与仿真的周期性冲击信号相差不大，而后者的冲击不太明显，且在消除噪声的同时，冲击的幅值也大幅减小；从频域上看，前者的频谱在去掉噪声的同时与仿真信号的频谱比较接近，且不存在干扰的谱线，而后者则出现了大量的伪频谱成分，这样非常容易造成对故障信息的误判；从冲击的峭度信息上来看，前者的峭度比后者的峭度大，这也说明前者提取出来的冲击特征显著，有利于进行故障诊断。

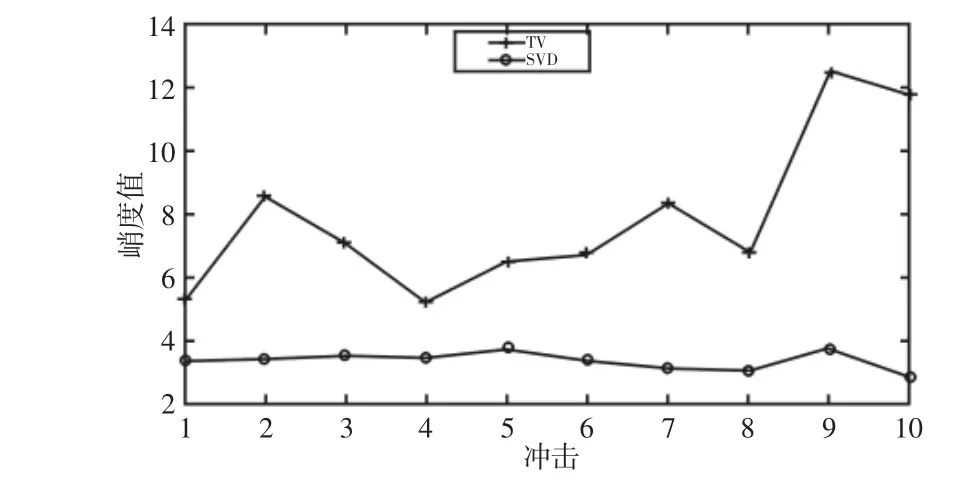
图5 单个冲击的峭度值对比Fig.5 Comparison of Kurtosis of Each Impact

5 轴承故障分析

为了验证全变差稀疏追踪算法对消除噪声、提取冲击特征、进行高速列车齿轮箱轴承故障诊断的有效性，搭建了齿轮箱轴承故障试验台，如图6 所示。

图6 齿轮箱轴承故障试验台Fig.6 Gear Box Bearing Failure Test Bed

由于实测信号中包含了不同频率的信号成分，直接对频率成分复杂的信号进行稀疏追踪无法对冲击特征进行有效地提取。为了避免其他频段的信号对冲击特征提取的干扰，引入具有抗频率混叠、平移不变等特点的DTCWPT 对振动信号进行分解。信号通过DTCWPT 分解得到一系列不同尺度的信号分量。为了选择其中冲击最为明显的信号分量，引入峭度指标，对重构回时域后的每一层信号计算峭度，选取其中峭度最大的一层作为待提取冲击特征的目标层。对该层信号分量进行全变差稀疏追踪提取信号中的冲击特征，并进行包络分析来检测故障。信号处理的具体流程，如图7 所示。

进行试验的齿轮箱轴承的具体参数，如表1 所示。该试验中，齿轮箱轴承的转速n=1597r/min，采样频率为100kHz。对存在外环故障的齿轮箱轴承做故障试验，采集的振动信号的时域波形，如图8 所示。

表1 轴承参数Tab.1 Bearing Parameters

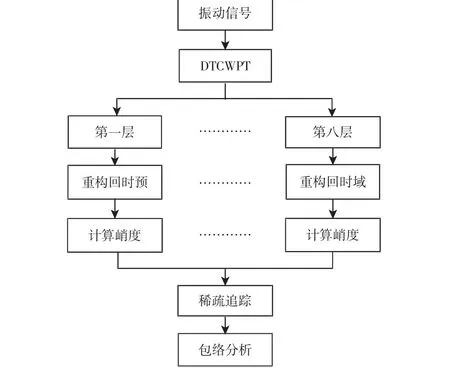
图7 信号处理流程Fig.7 Flow Diagram of Signal Processing

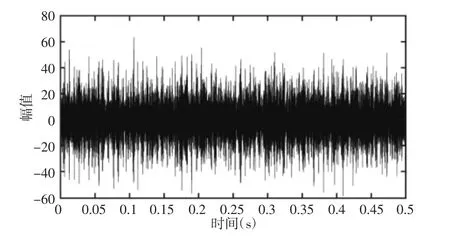
图8 外环故障轴承振动信号时域波形Fig.8 Time Domain Waveform of External Ring Fault Bearing Vibration Signal

根据式（15）可以计算得到轴承外环故障频率为144.6Hz。

选取原始数据进行DTCWPT 分解并重构回时域后的峭度最大的目标层数据作为示例。目标层的重构时域波形图，如图9所示。采用全变差稀疏追踪方法对该层数据消除噪声提取冲击，设置参数λ=2，得到优化后的时域波形及其包络功率谱，如图10所示。在图10（a）中可以看到，含冲击特征层的数据消噪后提取出的冲击特征明显，可以很清晰地发现周期性冲击单元，与轴承外环故障特征频率一致。在图10（b）中则可以清晰地看到外圈故障特征频率及其倍频。同样对图9 中的目标层信号进行SVD 去噪，得到消除噪声后的时域波形和包络功率谱，如图11 所示。

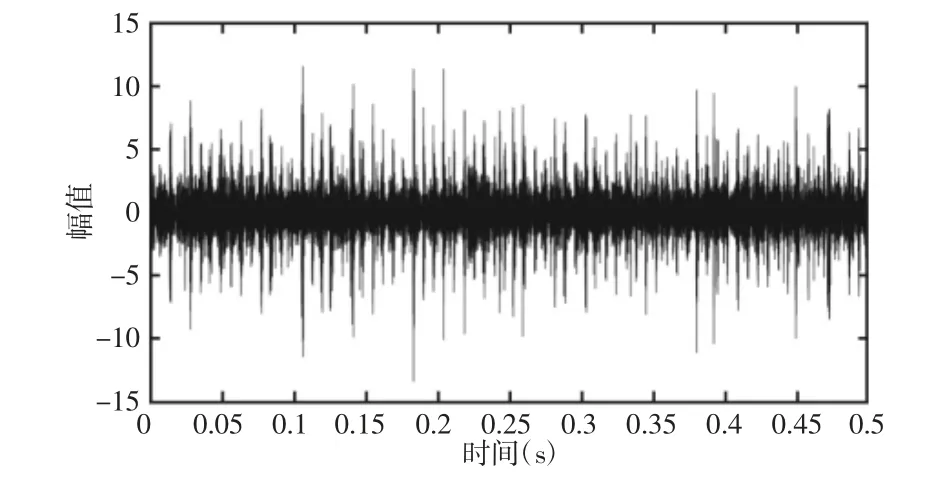
图9 目标层的时域波形图Fig.9 Time Domain Waveform of the Target Signal Component

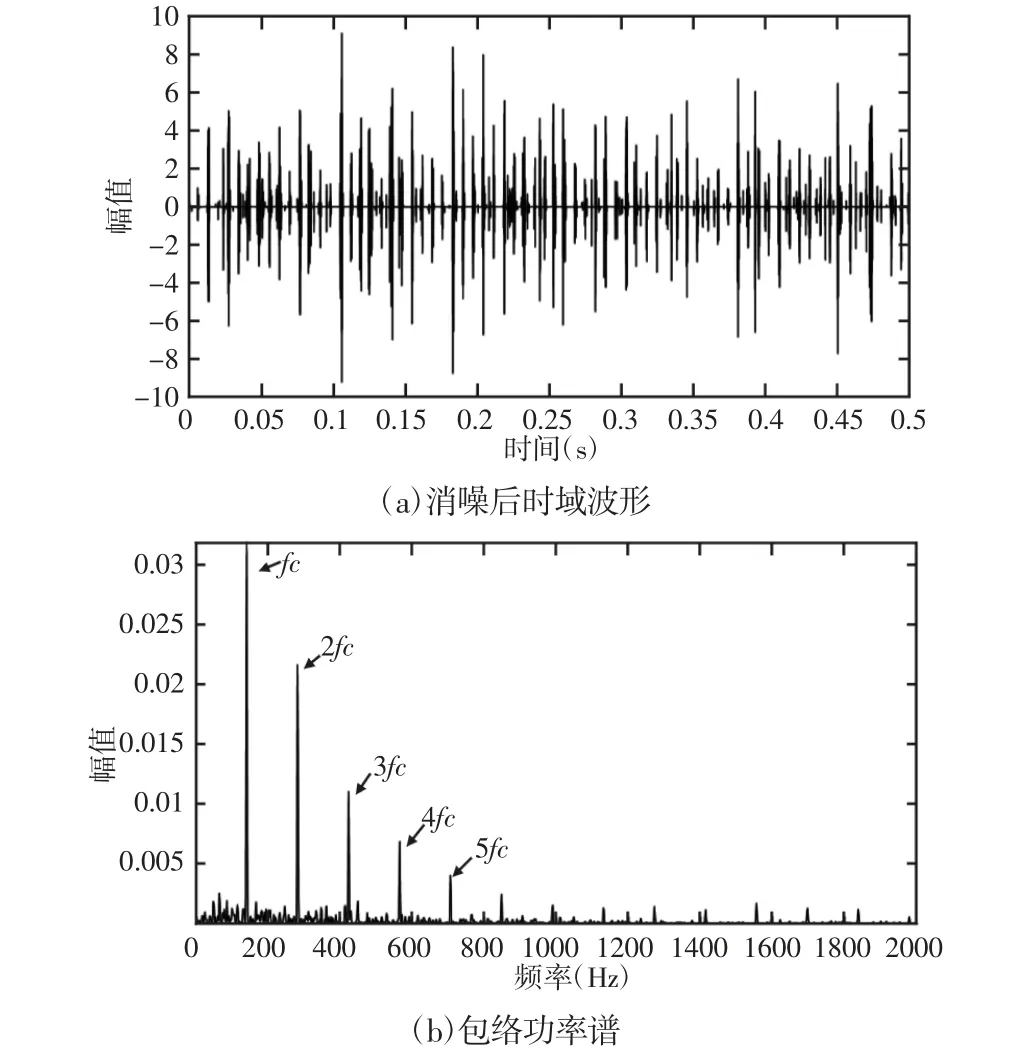
图10 稀疏追踪法消噪后时域波形及包络功率谱Fig.10 Time Domain Waveform and Spectrum of Noise Elimination Result by TV Sparse Tracking Method

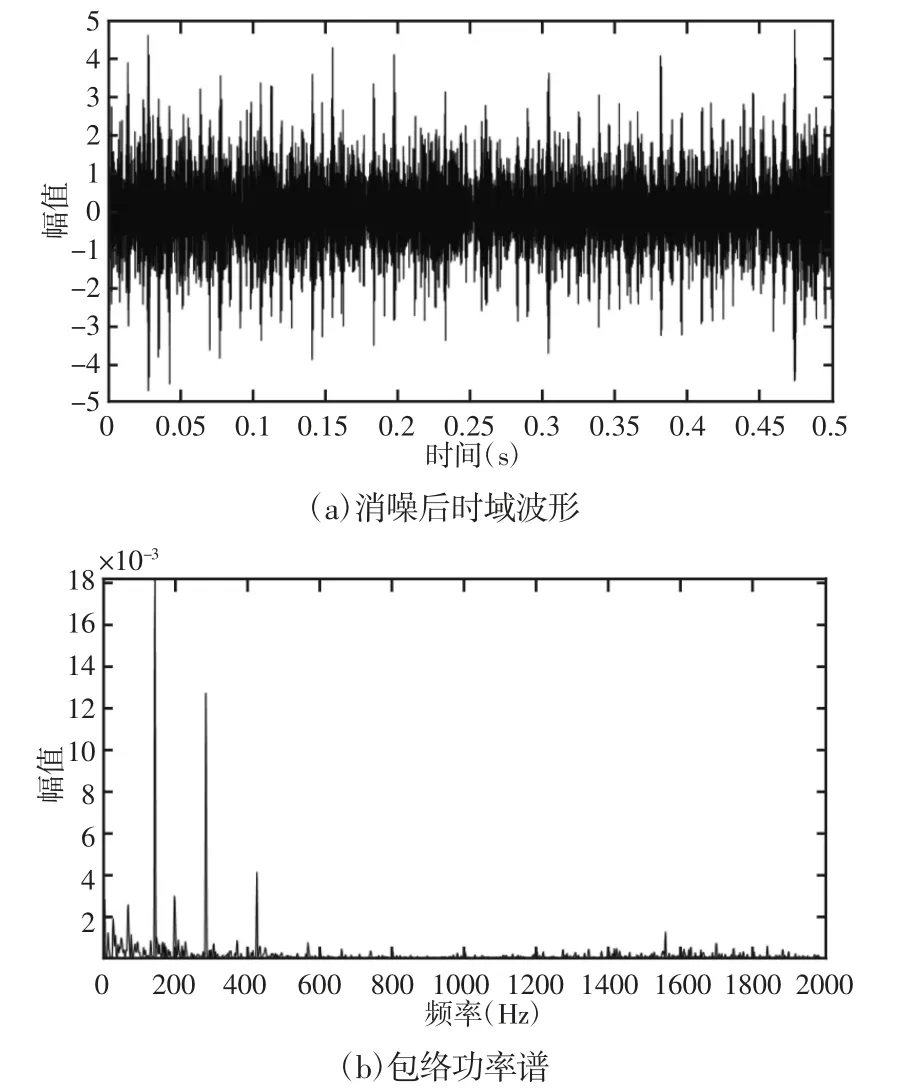
图11 SVD 法消噪后时域波形及包络功率谱Fig.11 Time Domain Waveform and Spectrum of Noise Elimination Result by SVD

对比图11 和图10，可以很明显地看出，提出的方法在消噪后冲击更加明显，并且故障表现形式更加丰富，效果更好。

介绍的方法通过使用DTCWPT 可以将信号划分成不同频段的信号，通过全变差稀疏追踪方法则能够将目标层中与冲击成分在同一频段的噪声去除。从处理的结果可以看出，信号时域中的周期冲击特征更加明显，并且谱线清晰，便于故障诊断。

6 结语

通过DTCWPT、全变差稀疏追踪方法的有机结合，提出的方法概括起来有以下特点：

（1）充分利用了DTCWPT 划分频带的平移不变形、抗频率混叠性，充分利用了全变差稀疏追踪方法对提取冲击特征以及去除噪声的独特优势。

（2）两种方法的结合提高了各个尺度信号的清晰度，有力地凸显了故障特征。

（3）该方法能够捕捉到故障的基频、倍频等特征，具有一定的工程应用前景。