车辆紧急避让路径跟踪神经网络自抗扰控制

贠海涛，曾 欣，林晋召，李佳月

（青岛理工大学机械与汽车工程学院，山东 青岛 266520）

1 引言

随着信息科技的不断进步，车辆控制技术也不断向着智能化、联网化方向发展。车辆的高速紧急避让技术根据车与车、车与障碍物之间的相对速度、距离、以及加速度等基本信息，控制前轮转角避让障碍物，保证车辆的安全行驶。而车辆在高速紧急避让的过程中，存在较强的不确定性，所以高速紧急避让过程中的路径跟踪是智能车辆发展进程中亟待解决的关键性问题[1-2]。

对于高速紧急避让工况下路径跟踪控制器的设计，国内外学者大多采用最优控制、鲁棒控制以及模糊PID 控制等人工智能方法或者线性二次规划方法[4-8]。文献[3]采用前馈加状态反馈设计路径跟踪器，实际方向盘转角由前馈和反馈两部分组成；文献[4]设计了一种运用预测控制方法对主动前轮转向和车轮力矩共同控制的紧急避障控制器；文献[5]首先根据车辆与障碍物的相对距离生成期望的避障路径，然后设计了滑模控制路径跟踪控制器。文献[7]采用最优控制方法设计了三自由度汽车模型的路径跟踪控制器；文献[8]采用了自抗扰控制（ADRC）方法设计了高速紧急避让工况下路径跟踪控制器。但这些方法存在自适应差、依赖于精确模型或者抗干扰能力弱等缺陷。神经网络（BP）自抗扰控制方法可以不依赖系统精确的模型，能够观测出系统参数的变化并且补偿掉，具有很强的鲁棒性。相对于常规的自抗扰控制方法，神经网络自抗扰控制能够在线调节扩张状态观测器（ESO）参数，抗干扰能力更强、范围更广，控制效果更好。

2 侧风干扰下的车辆动力学模型

假设侧向风垂直作用于汽车直线行驶方向，风压中心与车辆质心距离为e，引起的侧向力、横摆力矩分为Fw、Mw（取绕车辆质心逆时针方向为正），其数学模型具体如下：

式中：A—车辆迎风面积，m2；ρ—空气密度，kg/m3；ux—车辆直线行驶速度，km/h；uw—侧向风速度，km/h；Cy—侧向风力系数。将整车的转向模型简化为车辆二自由度模型[9]，如图1 所示。

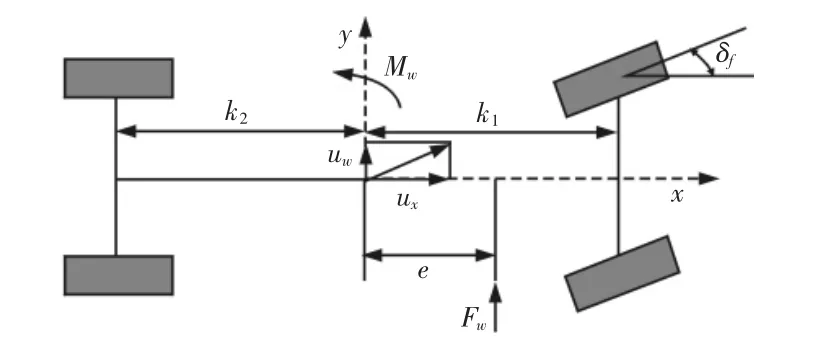
图1 侧风干扰下车辆二自由度模型Fig.1 Two-Degree-Freedom Vehicle Model Under Crosswind Disturbance

以前轮转角为模型输入，不考虑转向系统、悬架的作用，并忽略路面不平、空气阻力的影响以及由于载荷的变化而引起左右两轮轮胎特性的变化，可得侧风干扰下的车辆二自由度运动学状态方程为：

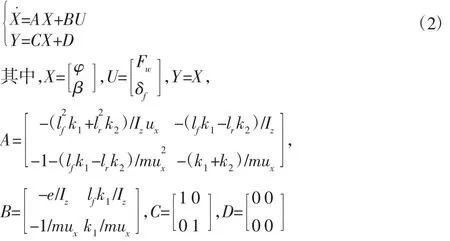
式中：m—车辆质量，kg；Iz—横摆转动惯量，kg·m2；lf、lr—车辆质心到前后轴的距离，m；k1、k2—前后轮侧偏刚度，N/rad；β—车辆质心侧偏角，rad；Mw—侧向风产生的横摆力矩，N·m；Fw—侧向风引起的侧向力，N；φ—车辆质心横摆角速度，rad/s；δf—前轮转角，rad。

3 路径规划

由于Sigmoid 函数曲线连续，且能满足避让过程中起点与终点处的曲率为0 以及最大侧向加速度约束，所以本次紧急避让跟踪路径采用Sigmoid 函数曲线。具体避让路径规划，如图2 所示。

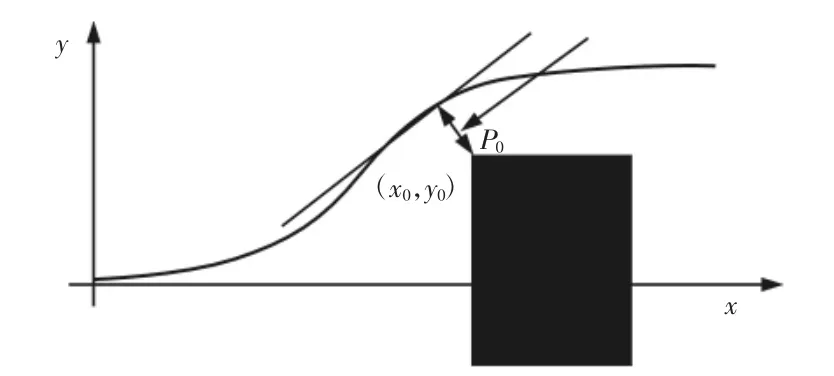
图2 高速紧急避让路径规划Fig.2 Path Planning for High Speed Emergency Avoidance

假设避让起始处横向位移为0，可得Sigmoid 函数曲线及约束条件方程如下：

式中：g、h—Sigmoid 曲线的参数，可通过约束方程求解；（x0，y0）—点P0的坐标；l—安全距离，m；aymax—车辆最大侧向加速度，m/s2。这里取aymax=0.6μmg，其中 μm、g 分别为路面附着系数和重力加速度。

4 神经网络自抗扰控制器设计

4.1 紧急避让路径跟踪控制策略结构

采用神经网络ADRC 通过控制输出到车辆模型中的前轮转角来实现对规划避让路径的精确跟踪，其整体控制策略结构，如图3 所示。为了提高ESO 的估计精度以及整个ADRC 的控制效果，在ADRC 内部嵌入通过BP 神经网络自适应的ESO，其具体结构，如图4 所示。

图3 高速紧急避让路径跟踪控制策略框图Fig.3 Block Diagram of Path Tracking Control Strategy for High Speed Emergency Avoidance

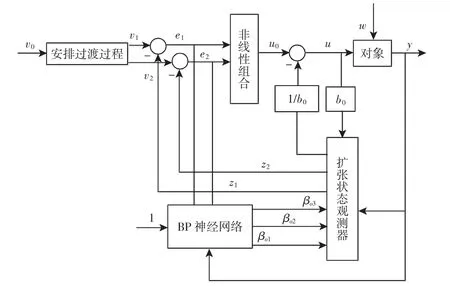
图4 神经网络ADRC 结构框图Fig.4 Block Diagram of Neural Network ADRC

自抗扰控制是不完全依赖系统模型的一种控制方法，也是一种基于过程误差来补偿和消除误差的有效方法。ADRC 主要由跟踪微分器（TD）、非线性组合（NLSEF）以及扩张状态观测器（ESO）三部分组成。

4.2 跟踪微分器

跟踪微分器可实现输入信号的快速跟踪，并输出跟踪信号的微分，用来安排过渡过程。其数学模型如下：

式中：v0—控制器输入信号；v1、v2—v0的跟踪信号；h—仿真步长；r0—可调参数；fhan（x1，x2，r，h）—最速控制综合函数[10]。

4.3 非线性组合

NLSEF 是根据系统误差来输出合适的控制量，对于二阶被控对象，NLSEF 可以采用如下数学模型：

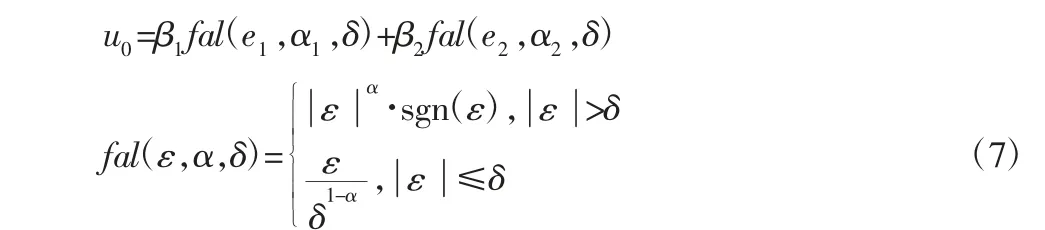
式中：fal（ε，α，δ）—原点附近具有线性段的连续幂次函数；δ—线性段的区间长度；α—非线性因子。

4.4 扩张状态观测器

ESO 是ADRC 的核心部分，根据系统的输入和输出来估计系统的状态和总的扰动，并通过反馈加以补偿。三阶ESO 数学模型[11]如下：

式中：z1、z2—被控对象输出y 的跟踪输出信号、跟踪输出微分信号；z3—被控对象的总和扰动。

4.5 基于BP 神经网络的参数整定

由图4 可知，神经网络ADRC 较常规ADRC 多出一个用于ESO 三个重要参数 β01、β02、β03整定的BP 神经网络[12]。本次设计的神经网络采用3 层4-7-3 结构，即4 个输入节点、7 个隐含层节点以及3 个输出节点。

5 联合仿真试验

为了验证所设计的模型，首先在Matlab/Simulink 仿真平台搭建路径跟踪神经网络ADRC 模型，然后嵌入到软件Carsim 中去，并利用Carsim 提供的某款车型进行控制器的联合仿真，所选取的车辆模型基本参数，如表1 所示。当车辆在路面附着系数为0.800 的路面，分别以纵向速度60km/h、100km/h 高速行驶时，取侧向风最大速度为60km/h，则侧风力系数为0.900，并选取空气密度ρ=1.225kg/m3，车辆正面投影面积A=2.108m2，可得不同车速下阶跃阵风干扰，如图5 所示。

表1 车辆参数Tab.1 Vehicle Parameters

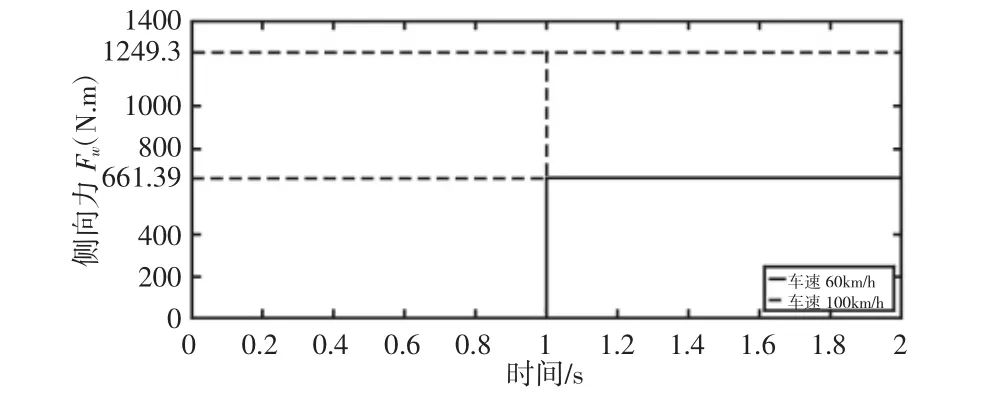
图5 不同车速下60 km/h 阶跃阵风干扰Fig.5 Step Gust Disturbance of 60km/h of Different Vehicle Speed

为了验证所设计的神经网络ADRC 以及与常规ADRC 作对比分析，神经网络ADRC 和常规ADRC 相同部分参数均选择如下：TD 参数：r=10 000，h0=0.0006；NLSEF参数：β1=120，β2=120，α1=0.250，α2=0.950，δ=0.010；ESO 参数：α01=0.050，α02=0.750，h=0.001，δ=0.010；设计参数b0=500。另外常规ADRC 参数 β01、β02以及 β03分别取200000、0.010 以及2000。针对车辆模型，依次加入无阵风干扰、10km/h 阵风干扰以及60km/h 阵风干扰三种情况进行验证，路径跟踪效果，如图6～图8 所示。

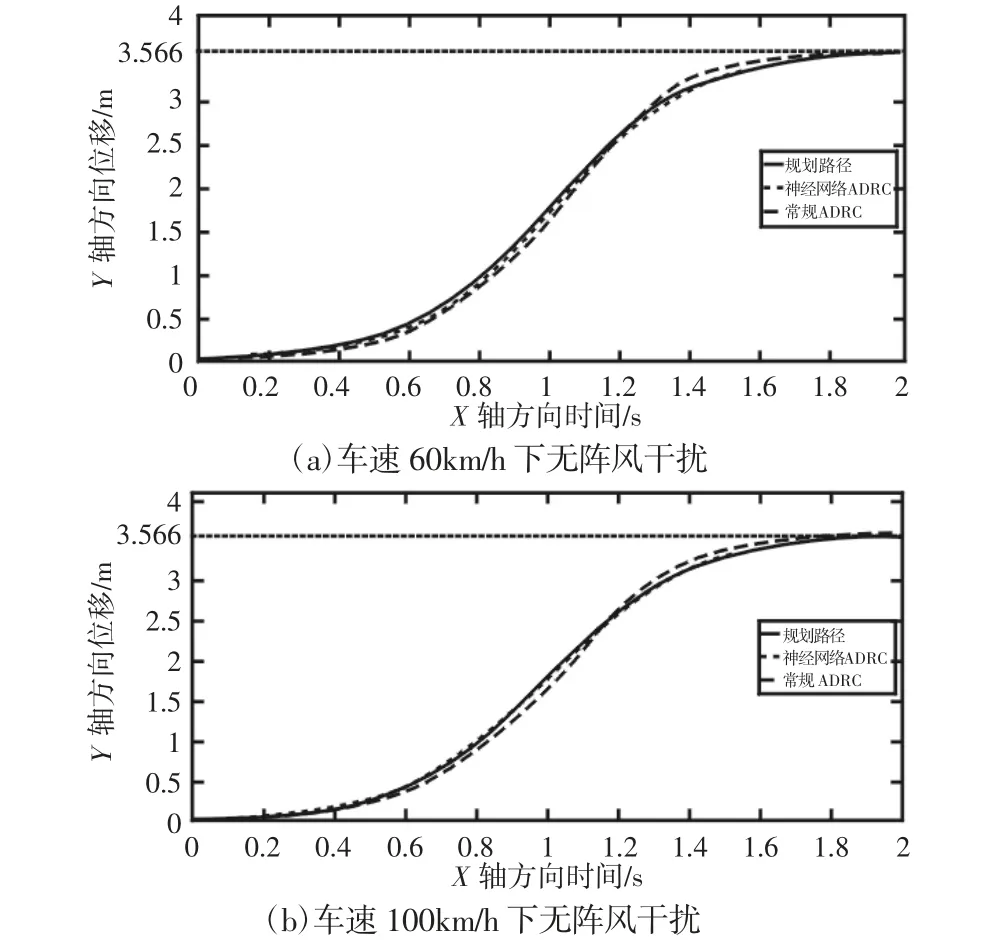
图6 不同车速下无阵风干扰时路径跟踪效果Fig.6 Path Tracking Effect without Gust Interference of Vehicle Speed of Different Vehicle Speed

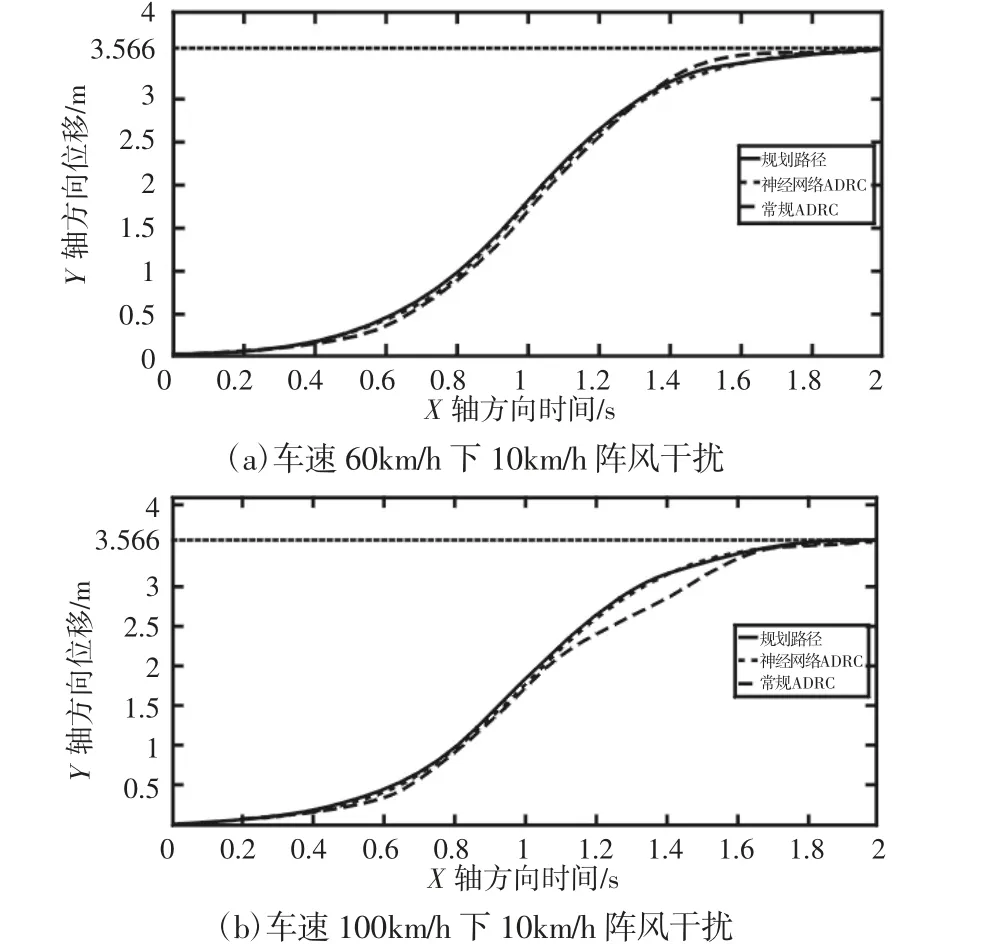
图7 不同车速下10 km/h 阵风干扰时路径跟踪效果Fig.7 Path Ttracking Effect in Gust Interference of 10km/h of Different Vehicle Speed

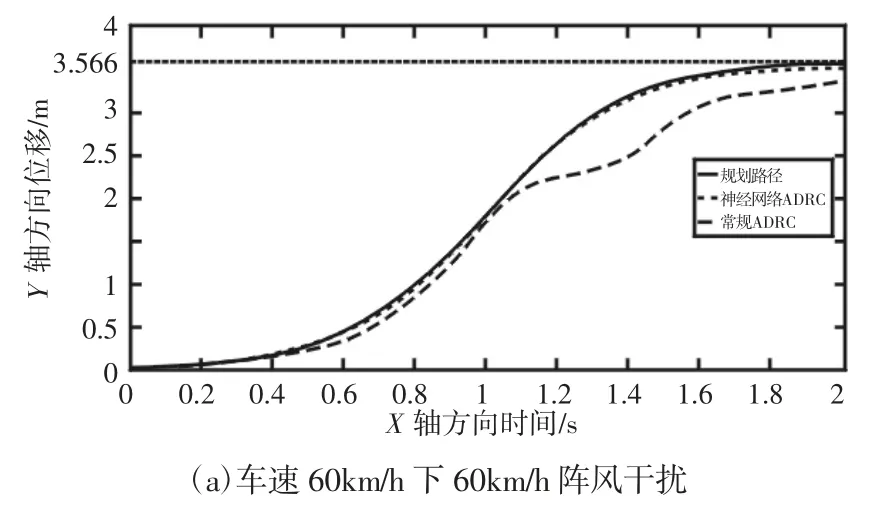
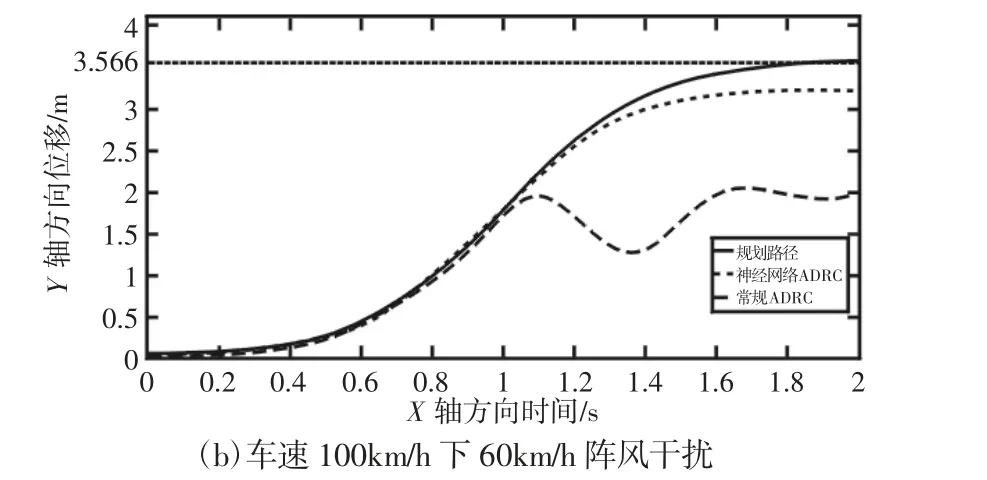
图8 不同车速下60 km/h 阵风干扰时路径跟踪效果Fig.8 Path Tracking Effect in Gust Interference of 60km/h of Different Vehicle Speed

从图6～图8 看出，对于同一车速下不同风速的阵风干扰，神经网络ADRC 的抗干扰能力较常规ADRC 更强，对系统总扰动估计精度更高，比如在车速100km/h 下60km/h 的阵风干扰时，两者路径跟踪效果差别最为明显，神经网络最大跟踪误差为9.82%，而常规ADRC 最大跟踪误差达到58.70%；当阵风干扰相同，车速由60km/h 提高到100km/h 时，常规ADRC 抗干扰能力变弱，对路径的跟踪效果下降很快，而神经网络ADRC 仍然能够保持很高的跟踪精度，且控制量的震荡幅度明显更小。

6 总结

针对车辆高速紧急避让过程，采用Sigmoid 函数进行路径再规划，考虑由于外界干扰不确定等因素，常规ADRC 存在控制精度较差、效果不尽人意的问题，设计了神经网络ADRC。Carsim/Simulink 联合仿真结果表明：（1）通过神经网络在线调整ESO 参数能够有效地提高ADRC 的性能以及车辆在高速紧急避让过程中路径的跟踪精度，并降低参数整定的难度；（2）神经网络ADRC较常规ADRC 更具优越性，比常规ADRC 的抗干扰能力更强，且在100km/h 车速下60km/h 侧向风干扰时，两者最大跟踪误差分别为9.82%、58.70%。