基于MATLAB和ADAMS的电池阵展开动力学分析

李盘浩， 张 静， 杨 振， 寇子明

（太原理工大学机械与运载工程学院，太原030024）

0 引 言

太阳电池阵是航天器进入轨道后的主要能量来源，对于卫星的正常工作有着重要作用［1-3］。由于展开和锁定过程中会造成卫星的振动，不利于空间姿态的控制［4-5］。因此对在轨工况下的太阳电池阵展开过程进行仿真分析，为卫星的结构设计提供依据，具有十分重要的实际意义［6］。

金咸定［7］利用第二类拉格朗日方程建立了太阳电池阵展开的数学模型，并用龙格-库塔方法计算。游斌弟等［4］利用Lagrange 和Newton 方法推导出了太阳电池阵系统递推动力学模型，采用非线性弹簧阻尼作为接触碰撞约束力，构建太阳电池阵展开过程的广义动力学模型。金光等［3］研究了卫星帆板展开对整星姿态的影响，优化了展开策略。对单块帆板的展开进行了理论建模，得到了转动角度和时间关系的解析解。刘铸永等［8］考虑太阳电池阵的刚柔耦合效应，基于Hertz接触理论，建立锁销和锁槽的碰撞模型。Zhang等［9］和Gao等［10］分别研究了采用不同机翼展开方式的串翼无人机在展开过程中的动态气动特性和铰链力矩变化。

太阳电池阵在展开过程中会对卫星本体造成冲击，引起本体姿态的变化，因此展开过程的动力学尤为重要。本文对一种含超弹性铰链的电池阵展开进行了动力学分析，用Adams软件建模，进行动力学分析，改变铰链的峰值力矩和平衡力矩，分析对折展机构动力学性能的影响，使用第二类拉格朗日方程进行建模，并用Matlab进行求解来验证Adams建模的正确性。

1 模型建立

1.1 三维模型建立

为分析超弹性铰链对展开过程的影响，先建立分析机构的三维模型如图1 所示：

1.2 ADAMS仿真模型

Adams 具有完备的建模与分析功能［11］，用ADAMS建模较为方便。本文用ADAMS 建立实体模型，并添加约束。

Adams中拥有固定副，齿轮副与旋转副等运动副。具体到本文中的太阳帆板，卫星本体采用固定副；卫星本体、连接架和基板之间的连接采用旋转副，运动副上将添加驱动力。

在太阳帆板展开过程中，施加扭转弹簧（Torsion Spring）来驱动各个关节运动。扭转弹簧刚度为50 N·m／ rad，阻尼系数为2 N·m·s／ rad。在扭转弹簧上设置驱动力，预设转角弹簧1 即卫星本体与帆板连接处的扭转弹簧为π／ 2，弹簧2 即外帆板与内帆板处的扭转弹簧设置预设转角为π。如图2 所示。

1.3 仿真模型验证

为了验证Adams中模型的正确性，利用第二类拉格朗日方程建立动力学方程，并用Matlab 进行求解，对比二者的角度随时间变化曲线来验证ADAMS 仿真模型。

（1）动力学分析模型的建立。该电池阵有两个太阳帆板组成，太阳帆板之间以及太阳帆板和卫星本体之间由扭转弹簧铰接而成，分析模型如图3。内、外板长度为2l。C1为内板质心，C2为外板质心，内、外板质量分别为m1和m2。

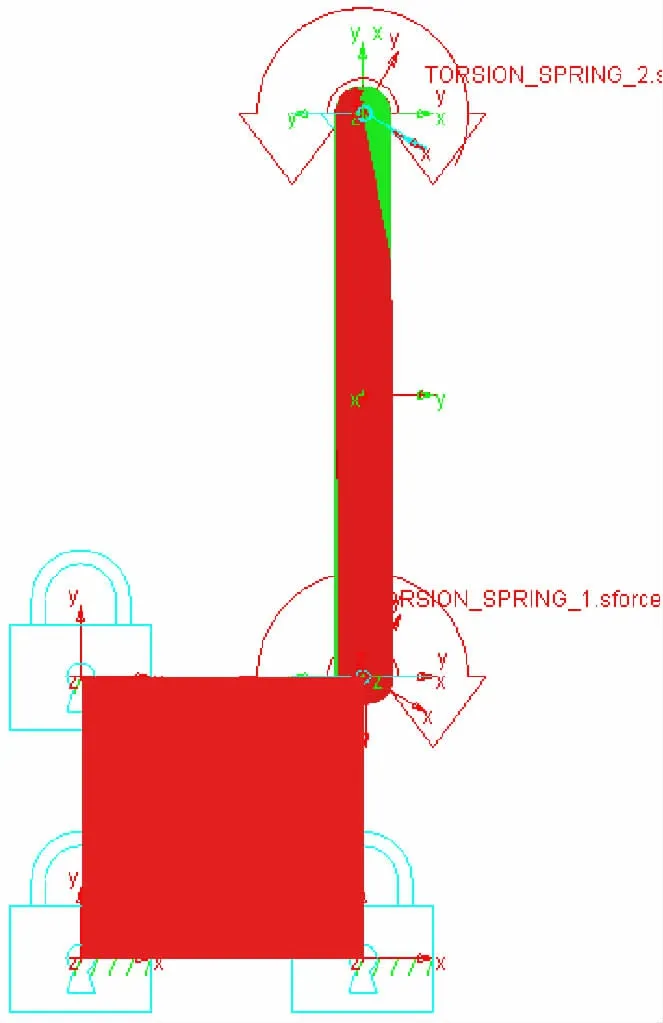
图2 ADAMS仿真模型

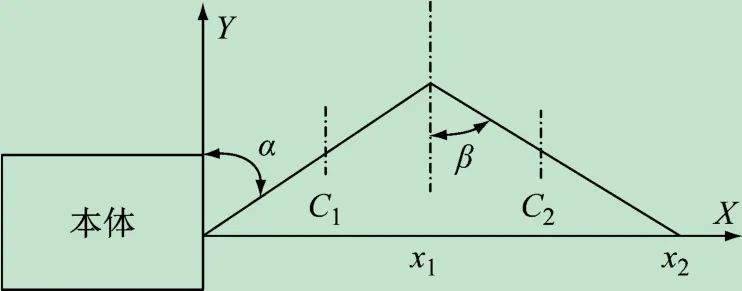
图3 折展机构动力学分析模型

（2）动力学方程的建立。图3 将卫星本体视为刚体，且无自由度。x、y 轴为固定在星体上的坐标系。太阳帆板在铰间扭簧驱动力矩下展开，展开过程中，太阳帆板还受到弹簧阻尼的作用。用第二类拉格朗日方程［12-13］来建立太阳帆板的展开运动规律：

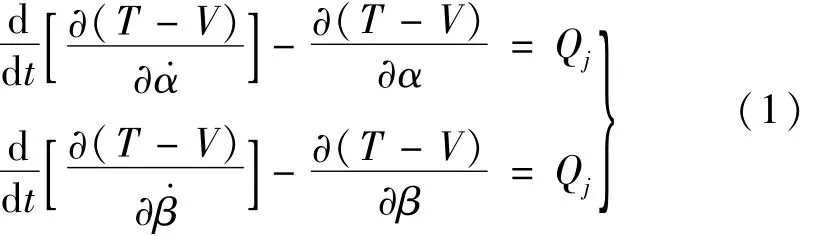
式中：T为太阳帆板系统动能；V 为系统势能；Qj为太阳帆板系统非有势力。非有势力为扭簧提供的初始力和扭簧的阻尼力。

内、外板的质心运动方程为：

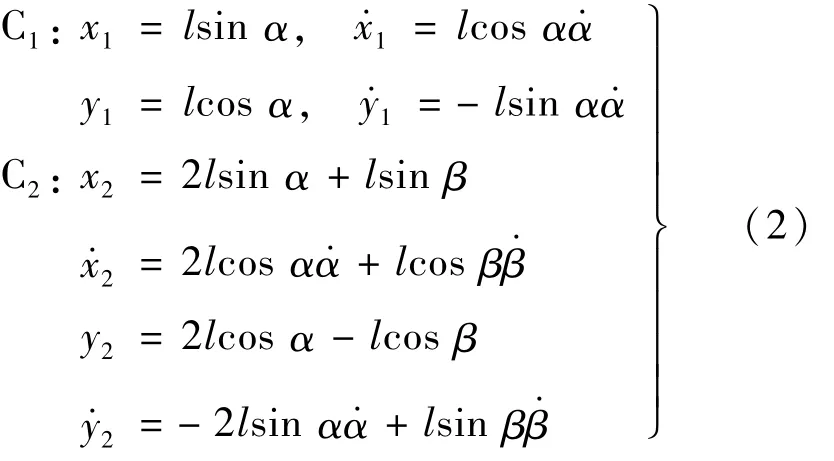
因为内、外板的动能又分为平动动能和绕质心的转动动能，在展开过程的某一时刻，太阳帆板的动能为：

（1）针对MWD仪器工具面角差测量方法及仪器落后的问题，设计了一种新型激光式MWD角差测量仪，并介绍了其工作原理和工作步骤，相对于目前现场采用的工具面角差测量工具及方法，激光式MWD工具面角差测量仪具有准确度高、精度高、成本较低、操作简单等特点。

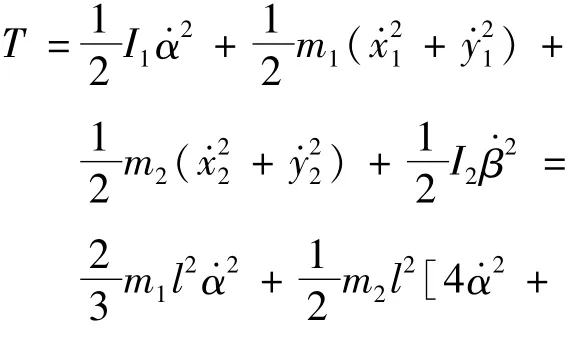
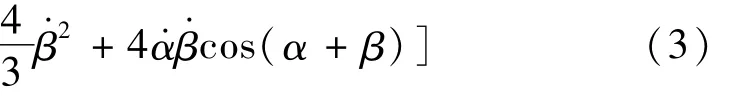
式中：I1为内板的转动惯量；I2为外板的转动惯量。

太阳帆板系统的势能是指铰间扭簧的弹性势能：

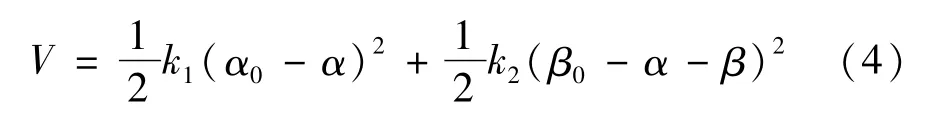
式中：α0、β0为扭簧的预紧角；k1、k2为扭簧的刚度系数。

太阳帆板在展开过程中受到弹簧的阻尼作用，为非有势力

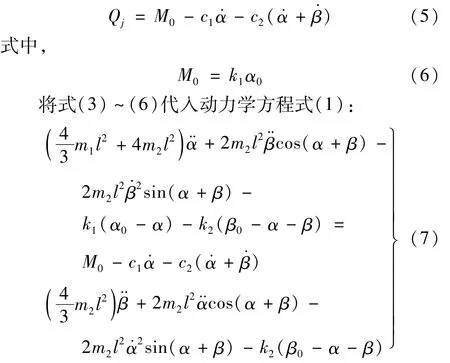
1.4 动力学模型验证

为了验证ADAMS 建模，在Matlab 中输入和ADAMS中相同的初始值，并将单位统一后将动力学方程输入Matlab 中进行求解。将方程边界条件输入Matlab［14］，代入驱动力矩、内、外帆板尺寸、质量等参数，即可解得内、外帆板转动角度随时间t的变化曲线。

本文条件为：杆件质量均为3 kg；杆长为0． 2 m；扭簧刚度为50 N／ m；阻尼为0． 4 N·m·s／ rad；α0为90°；β0为180°。

本文采用Matlab中的ode45 命令对动力学方程组进行求解，ode45 采用的是Runge-Kutta 算法［15-16］，并将ADAMS 中后处理的曲线导入到Matlab 中进行对比，结果如图4、5 所示。

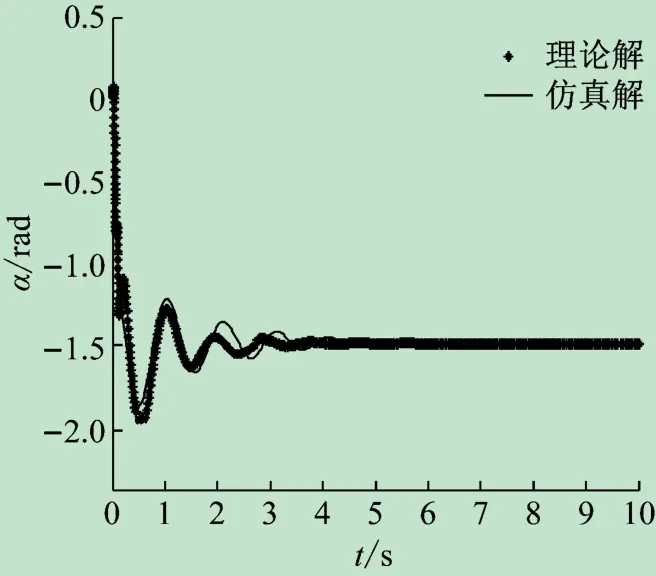
图4 内板仿真结果对比

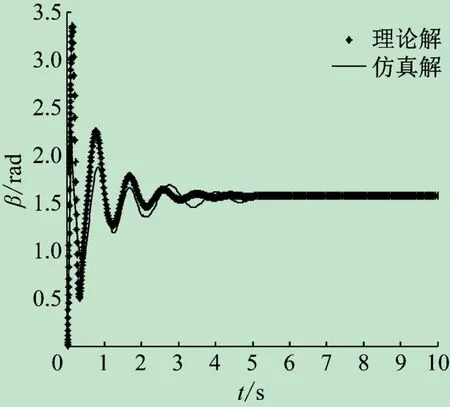
图5 外板仿真结果对比

由内、外板仿真结果对比结果，可以看出两种建模方式展开时间大致相同，展开过程运动轨迹相似，因此可知Adams中建模是正确的。

2 非线性特性分析

动力学模型验证后，将弹簧改为超弹性铰链，超弹性铰链展开力矩如图6 所示。［17］

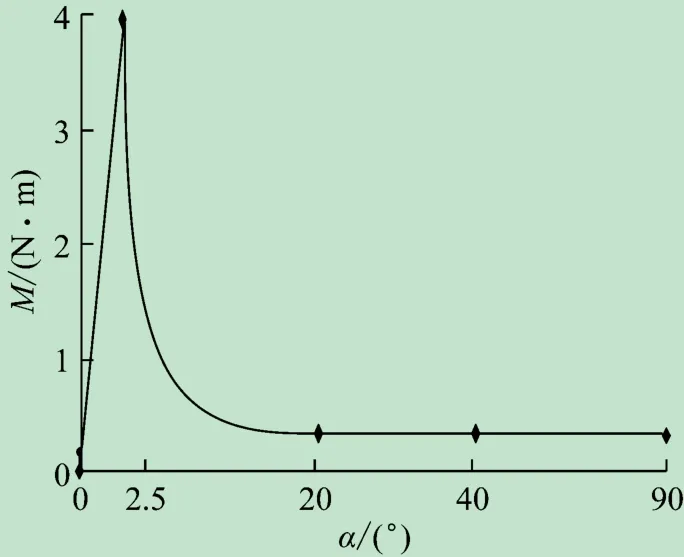
图6 超弹性铰链展开力矩

采用ADAMS 自定义函数，在ADAMS 中进行仿真，函数形式如下：

STEP（AZ（MARKER_2），0，0，2． 5 d，- 4）+

STEP（AZ（MARKER_2），2． 5 d，3． 64，20 d，0）+

STEP（AZ（MARKER_2），20 d，0，90 d，0）STEP函数添加在α处，仿真结果如图7 所示。

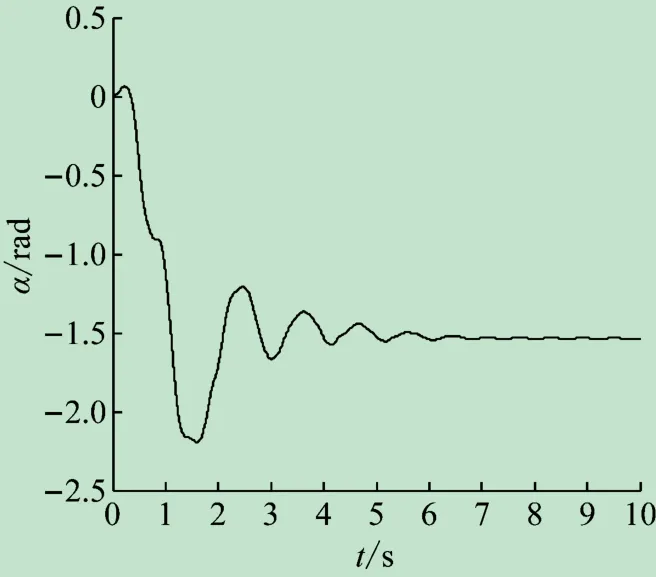
图7 内板展开结果

由图7、8 可知，内、外板在6 s 时展开，震荡幅度较小。

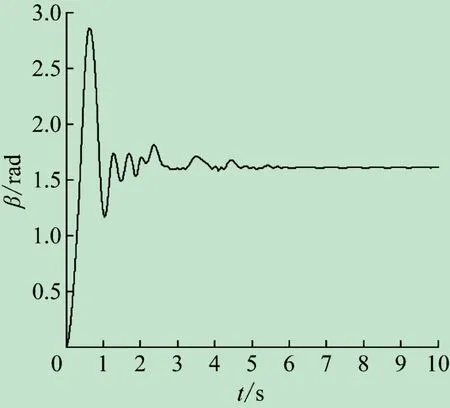
图8 外板展开结果

2.1 不同峰值力矩对动力学的影响

在上述验证Adams建模正确的基础上，不改变阻尼系数，改变力矩的峰值，即改变STEP 函数的最大值分析不同峰值力矩对动力学的影响，对比结果如图9～11 所示。

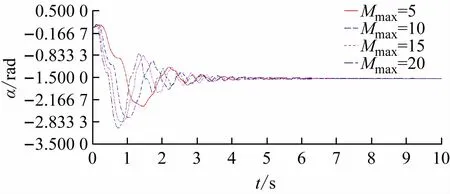
图9 不同峰值力矩下内板展开仿真对比

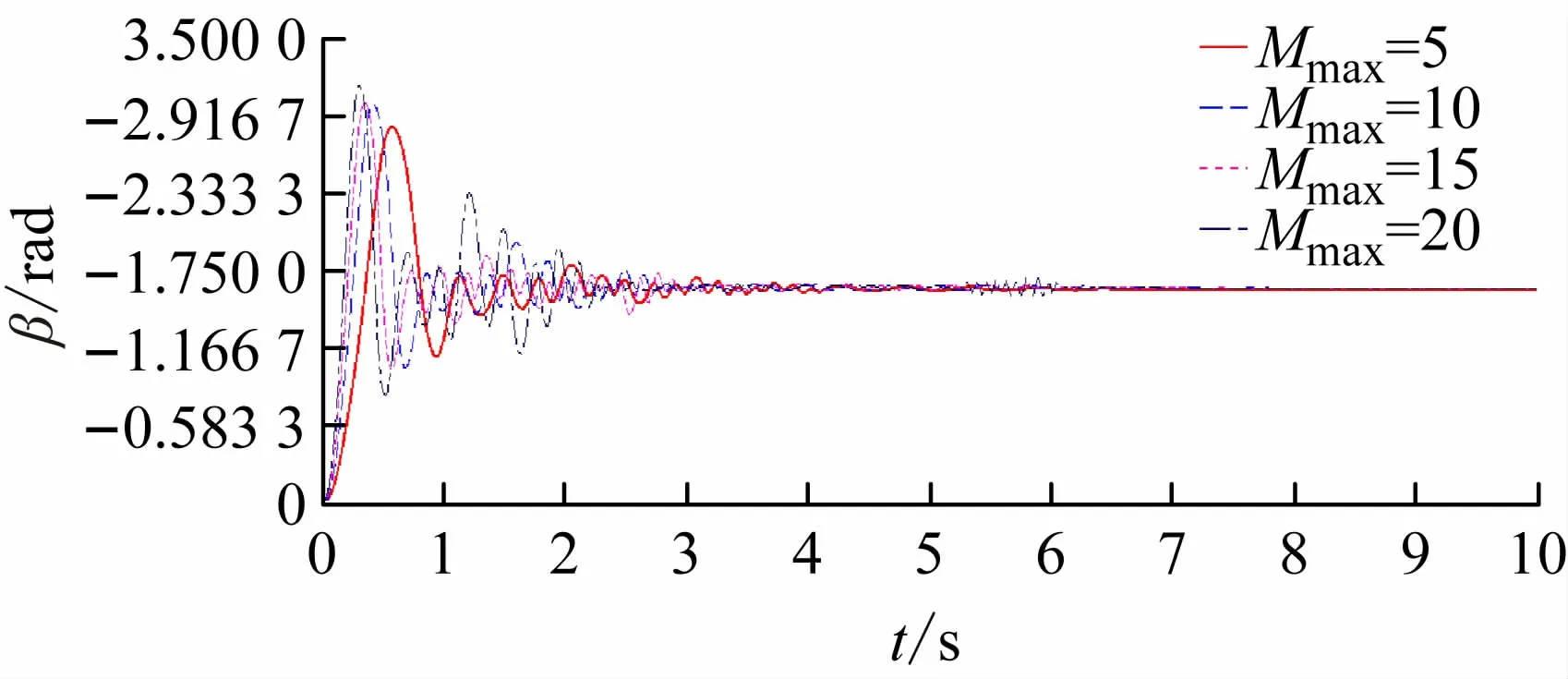
图10 不同峰值力矩下外板展开仿真对比

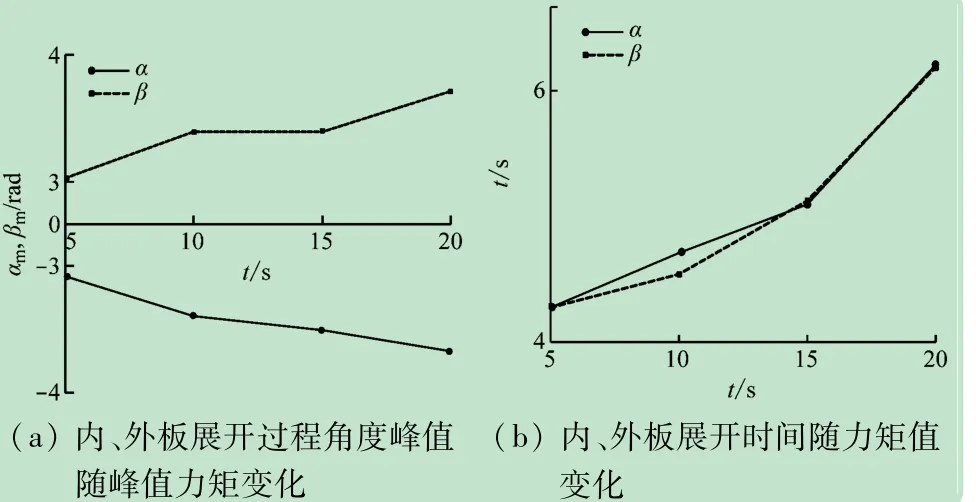
图11 内、外板展开随峰值力矩变化

由图9 ～11 可知，在不同的峰值力矩下，内、外板展开最大值随峰值的增加而增大，达到稳定时间也越长。

2.2 超弹性铰链平衡力矩值对动力学的影响

在峰值力矩不变的情况下，改变平衡力矩值，分析平衡力矩值对动力学的影响，对比结果如图12 ～14所示。

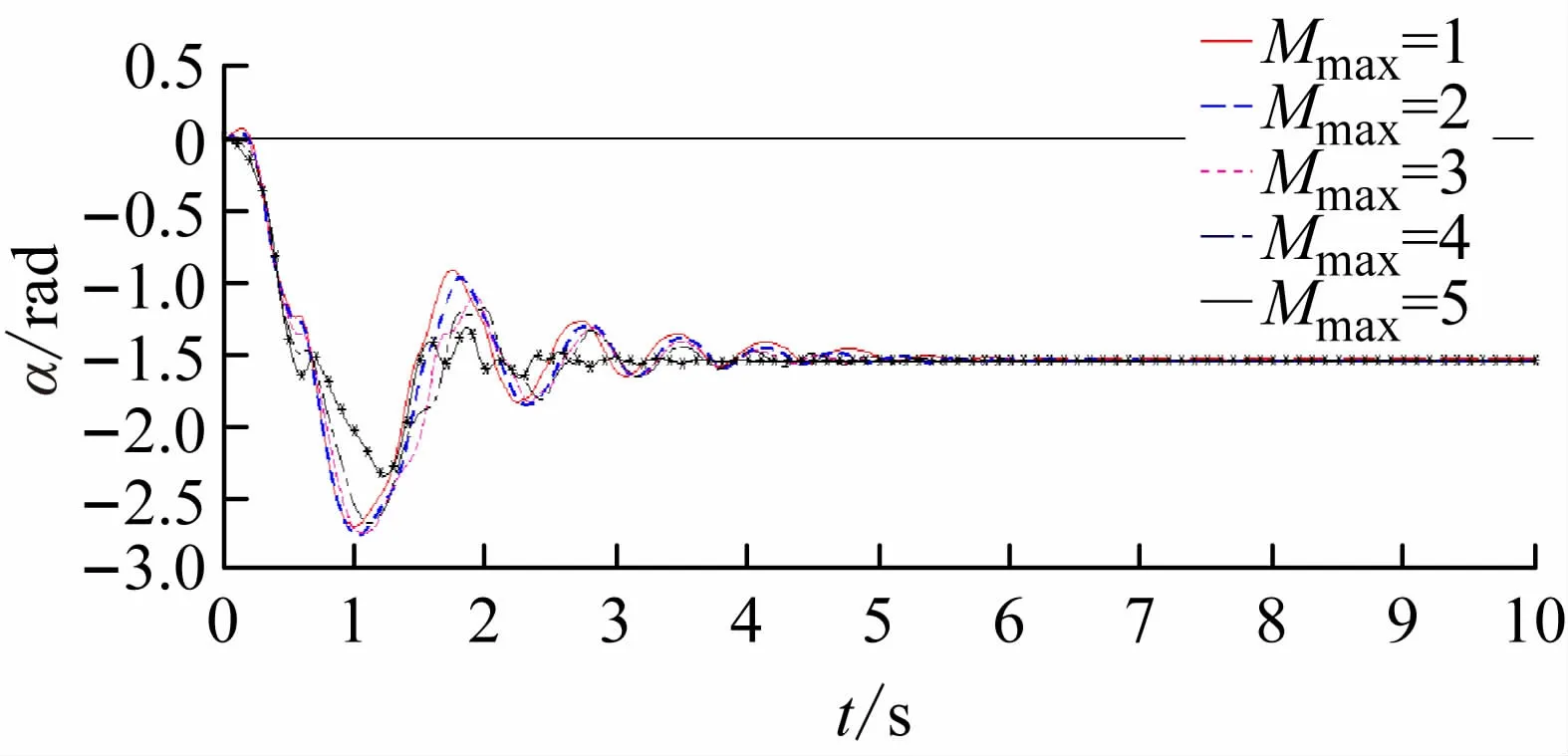
图12 内板展开仿真对比

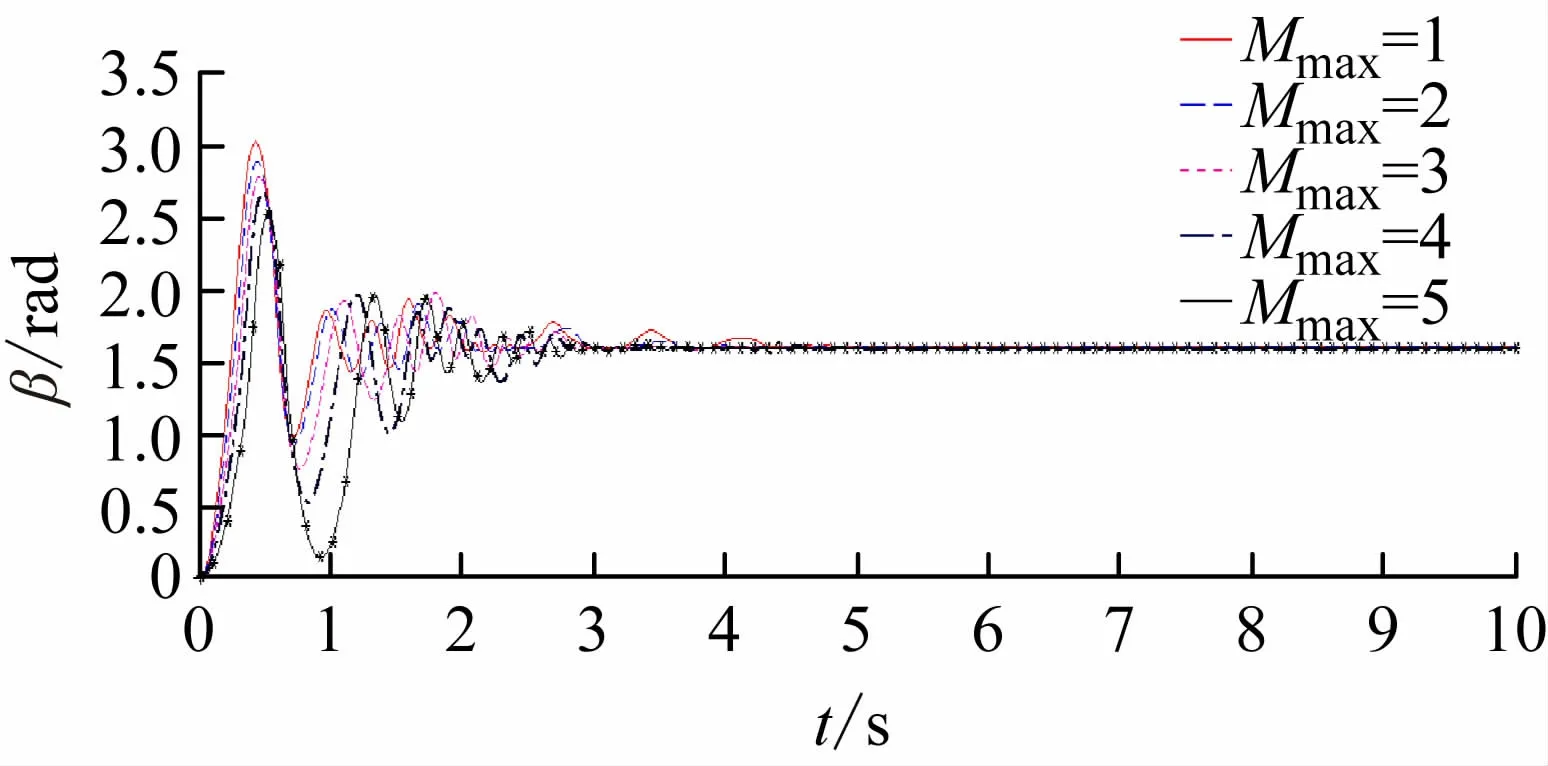
图13 外板展开仿真对比

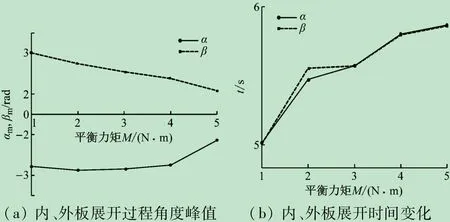
图14 内、外板展开随铰链平衡力矩值变化

由图12 ～14 可知，在峰值力矩不变时，改变平衡力矩值，平衡力矩值越大，展开角度峰值减小，展开时间越久。

3 结 语

（1）利用第二类拉格朗日方程推导出了2 板2 弹簧的折展机构的数学模型，为该类折展机构提供了理论依据；

（2）在Adams中建立了该折展机构的模型，并进行仿真，利用Matlab进行计算，验证了ADAMS中建模的正确性；

（3）Adams中改变峰值力矩和平衡力矩范围，在不同的力矩值下，内、外板展开峰值随峰值力矩增加而增大，达到稳定时间越久，震荡越久；在力矩值不变时，改变平衡力矩大小，随着平衡力矩值增加，展开角度峰值减小，展开时间会增大。