拉拔承载锚杆合理锚固长度的确定

李福海， 高 浩， 何肖云峰， 姜怡林， 冯志华， 张桂斌

（西南交通大学土木工程学院，成都610031）

0 引 言

锚杆支护在维护工程稳定和增强岩体强度方面有重要作用。锚杆作为主要受力构件，考虑到其锚固环境的不可见性，以及较为复杂的受力特点等，要得到锚杆锚固力的大小并非易事。一般情况下，需要通过拉拔试验才能测得锚杆的锚固能力，锚固长度的长短直接影响到锚固力的大小。若设计的锚固长度超出合理值，锚杆将不能得到充分利用；反之，结构质量将得不到保证，合理锚固长度对保证质量，节约成本有显著意义。国内外很多研究者对锚杆的锚固长度展开过研究。文献［1-4］中通过在黄土、非黏性土和硬沙土的实验环境下测出临界锚固长度。刘佳龙等［5］分析了不同锚固长度对围岩支护所产生的影响。王洪涛等［6］对试验数据进行分析整理后推导出锚固长度计算公式。文献［7-8］中根据不同曲线模型得出了锚杆在不同假设下的锚固长度算法。张雄等［9］考虑了界面黏结强度，提出了锚杆合理锚固长度的计算公式。

尽管对锚杆的锚固长度研究较多，但仍存在不足之处：①现有的理论锚固长度在实际运用中有困难，实际工程大多都依靠经验和试验确定锚固长度。②锚杆受力机理并不明确，对于锚杆的设计偏于保守，通常仅靠增加锚固长度来保证锚杆承载力。本文探究锚杆的合理锚固长度，建立了锚固长度的计算公式。

1 锚杆临界锚固长度计算

临界锚固长度与有效锚固长度是锚固长度的两大类。其中，若锚固长度大于等于临界锚固长度la时，即使继续增加锚固长度，锚杆的锚固能力也几乎不会提高。锚杆部分区段不处于工作状态，该情况下，锚杆最大极限拉拔力与锚固长度无关。研究临界锚固长度对锚杆实际应用具有关键作用［10］。有效锚固长度lb是在工作荷载作用下，处于工作状态的锚固段长度。因此，从各自定义能得到la≥lb。

可通过李怀珍等［10］锚固剂-围岩界面剪应力分布解析计算式得到锚杆临界锚固长度的计算公式。

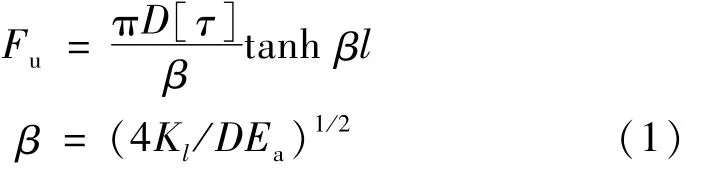
式中：K1（MPa ／ m）为界面剪切刚度；D（mm）为钻孔直径；锚杆与灌浆料的等效弹性模量

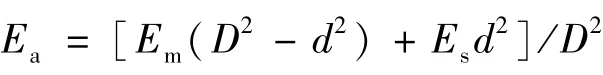
Em（GPa）表示锚固剂弹性模量，Es（GPa）为锚杆拉伸弹性模量；界面抗剪强度为［τ］（MPa）；锚固长度为l（m）；锚杆直径为d （mm）。

式（1）通过3 个假定对锚固段微元体进行分析，由平衡方程、物理方程以及几何方程经过推导演算得出，锚杆临界锚固长度的理论推导可由该表达式得到。在［τ］＝1． 5 MPa时，通过式（1）且保持其他控制变量不变，即可绘制极限承载力与锚固长度的关系曲线［11］，如图1 所示。

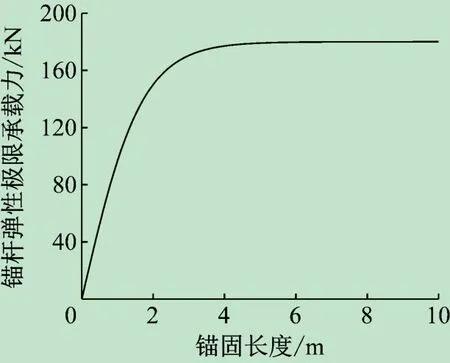
图1 极限承载力与锚固长度关系曲线

从图1 可以观察到，在荷载不大的前期阶段，锚固长度和弹性极限承载力成正比且线性相关。随后增长趋势逐渐平稳，承载力达到峰值后，不再随锚固长度的增加而有明显变化［12-13］，此时对应的锚固长度为锚杆的临界锚固长度。对于不同的界面抗剪强度，极限承载力和界面抗剪强度的变化曲线与极限承载力和锚固长度的变化曲线相似，随着［τ］增加，锚杆极限承载力先呈现一定的提高，后趋于平缓［11］。

由式（1）可以得到，当βl ＝5，tanh βl ＝0． 999 9≈1时，此时Fu达到峰值，记作Fu，max，

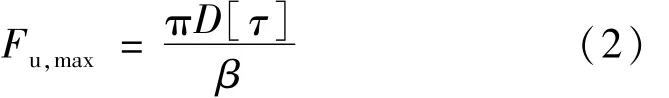
可以看出，当锚固长度达到临界值后，承载力达最大值，此后无明显变化，基本保持定值。所以，此时有βl＝5，而此时l为临界锚固长度la，即βla＝5。进而可得

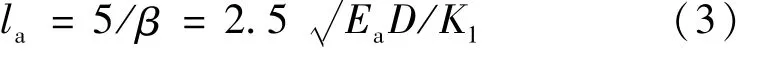
式中：Ea为等效弹性模量；D 与K1分别表示锚孔直径与界面剪切刚度。

由式（3）可知，界面剪切刚度与锚固长度临界值为负相关关系，等效弹性模量、锚杆孔径与锚固长度临界值为正相关关系。不同围岩之间的差异、锚杆自身参数的不同以及等效弹性模量的不一致，均会导致临界锚固长度有所差别［14］。

要得到锚杆临界锚固长度，主要确定界面剪切刚度K1的值［15］。在求解临界锚固长度的各种方法里，常常使用荷载传递法得出解析算式。锚固层的荷载传递采用理想化的弹塑性模型［16］，见图2。图中，K1表示剪切应力的强度大小。界面材料特性、灌浆压力、浆料充填程度等因素对K1均有影响。

实际工程中，通过拉拔试验的P - S 曲线关系可以求得界面的K1值。在李海洋等［15］所做的研究中，通过锚杆拉拔试验，反推出界面剪切刚度为

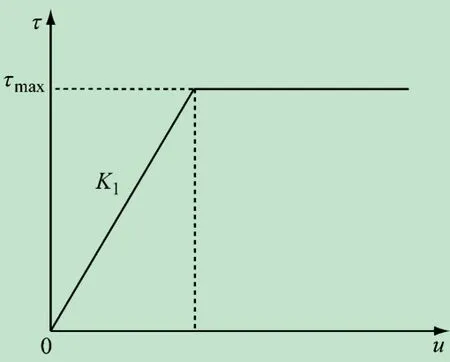
图2 锚杆理想弹塑性荷载传递模型［15］

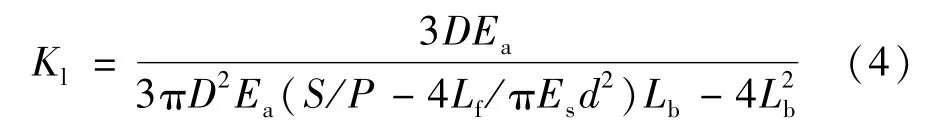
式中：Lf（m）是锚固自由段长度；Lb（m）为锚杆锚固段长度；Ea（GPa）是锚杆与灌浆料的等效弹性模量；S（mm）为端头滑移的位移；Es（GPa）为锚杆拉伸弹模；P（kN）为锚杆拉拔力；d（mm）为锚杆孔径大小；D（mm）是锚固体直径。

2 锚杆合理锚固长度确定

合理的锚固长度关系到工程实际。一方面，为了确定该锚固长度，需要确保结构不发生质量问题，也要综合考虑技术可实施性以及成本最优化等；另一方面，也要具备受力状态明确、易于施工、工期短以及对不同的地质环境有较强适应性和协调性等特点。锚杆合理锚固长度属于临界锚固长度的一部分，是主要受力段。锚杆在受拉拔过程中，产生的应力大部分处于锚固长度的前70%段，在后30%段应力分布不大［17-18］。由此可知，锚杆受力分布是不均匀的，主要集中在锚固体前70%段，而后30%段应力分布较小。在相关文献所做的研究中，给出了描述锚杆剪应力随锚固长度变化的曲线图，如图3 所示。

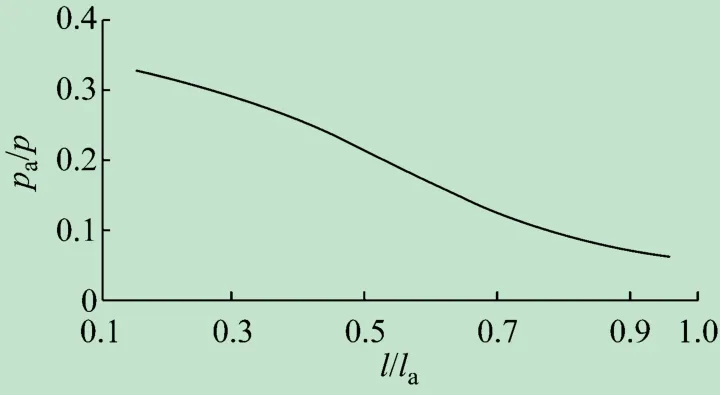
图3 剪应力分布曲线图

图3 中以锚杆后30%段承担荷载的比pa／ p 为纵轴，以锚固长度实际值l 与临界锚固长度la的比为横轴，得到该曲线分布图。从图中可看出，当锚固长度实际值与临界锚固长度相等时，锚杆后30%段所受荷载比不到7%；当锚固长度实际值为临界锚固长度50%

时，锚杆后30%段的荷载比重达到20%。在不超出锚固长度的临界值前提下，增加锚固长度，后1 ／ 3 段的承受荷载越小，反映出锚杆上的剪应力分布不均匀，从经济性和锚杆利用率来考虑，锚杆锚固长度实际值宜小于0． 5la。

由式（1）定义承载力与最大极限承载力比值

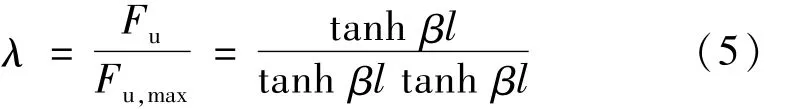
式中：λ为两个双曲正切函数的比值。为了方便分析讨论，作双曲正切函数tanh x的函数图，如4 所示。

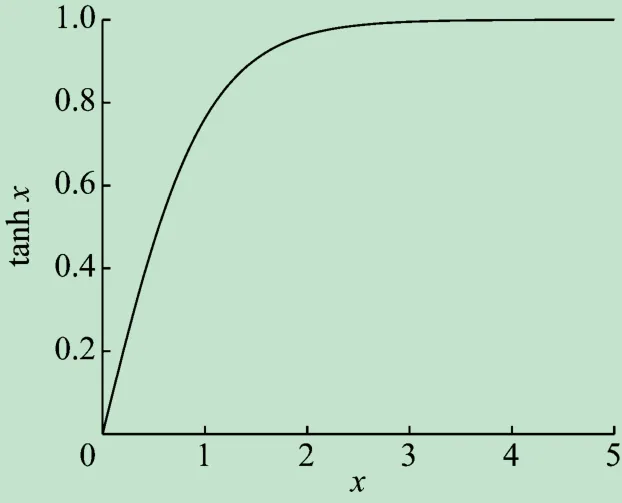
图4 双曲正切函数曲线

由图4 可知：x ＝3 时，曲线趋于平缓，tanh 3 ≈0． 999，趋近于1。对于式（5），当βl ＝3 时，tanh βl≈0． 999，Fu达到极值Fu，max，所对应的锚固长度为临界锚固长度la，即βla＝3。

为保证锚杆承载力，使其满足质量要求，取峰值拉拔力的90%作为锚杆荷载，得到锚杆合理锚固长度。即在式（5）中：取λ ＝0． 9，可得tanh βl ＝0． 9 tanh βla＝0． 9。当tanh βl ＝0． 9 时，此时锚固长度βl≈1． 5。由βl ＝1． 5，βla＝3，两式通过公式变换，相比较得到：l∶la＝0． 5。所以，在保证锚杆承载力要求的前提下，取锚固长度临界值的50%作为锚杆实际锚固长度，此时锚杆承受荷载为极限拉拔力的90%。

类似地，可以得出当λ取不同值时l／ la的结果，如表1 所示。

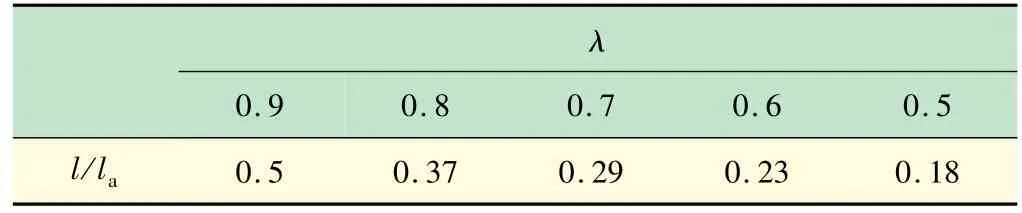
表1 不同λ值下实际锚固长度与临界锚固长度之间的关系

由表1 可知，随着锚杆锚固长度的减少，锚杆所能承受的拉拔力也逐渐减少，为了保证锚杆承载力，锚杆要留有足够的锚固长度。通过以上讨论，表明0． 5la

是确定锚杆锚固长度的重要指标，无论从成本因素还是锚杆承载力因素来考虑，应保证锚杆的锚固长度在0． 5la左右。在现有的研究中，也表明实际锚固长度大多落在0． 5la前后范围内，此后，增加锚固长度对锚杆极限拉拔力的提升并不明显。所以，实际锚固长度应取0． 5la，此值也就是锚杆的合理锚固长度l′a，表达式为：l′a＝0． 5la。由锚杆临界锚固长度代入可得：

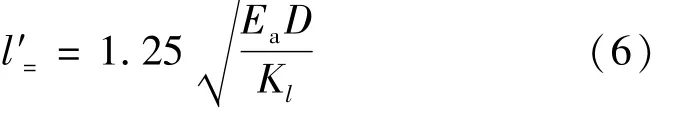
以提高锚杆工作有效性、经济性为前提，在临界锚固长度的基础上，减少锚固长度可以使得锚杆得到充分利用，同时锚固能力也可得到保证。

3 计算范例

引用张季如等［18］给出的一个具体实例对计算过程进行简单展示，同时验证理论公式的合理性。该实例为灌浆锚杆用于某深基坑支护，取其中一根锚杆进行计算演示，根据文献中给出的各参数值：锚杆自由段Lf＝5． 5 m，锚固段Lb＝17． 5 m，锚固体直径D ＝130 mm，锚杆直径d ＝25 mm，锚杆弹模Es＝20 GPa，锚固体等效弹模Ea＝40 GPa，由拉拔试验P - S曲线得：

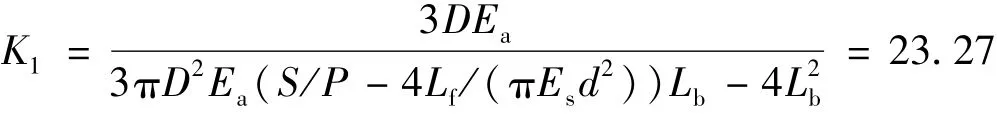
由各参数值数据可求得锚杆的理论临界锚固长度

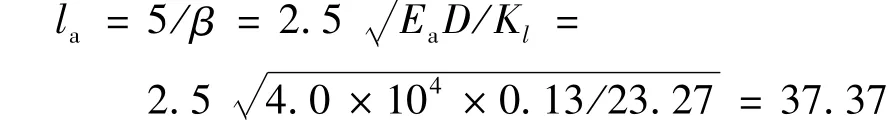
进而可以得出合理锚固长度：

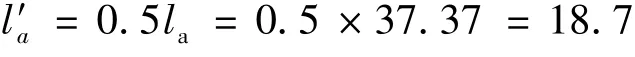
锚固长度与工程锚固长度接近，验证了合理锚固长度计算公式的有效性和合理性。

4 结 论

（1）实际工程中，为了提高锚杆抗拉拔力，单纯增加锚杆锚固长度会造成资源的浪费。因此，对锚杆锚固长度临界值的研究至关重要，算式

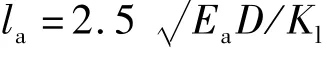
可用于计算锚杆临界锚固长度，有利于减少实际工程经济成本以及提高锚杆的利用率。

（2）临界锚杆长度la与界面剪切刚度K1为负相关关系，与等效弹性模量Ea、锚杆孔径D 为正相关关系。不同围岩之间的差异、锚杆自身参数的不同以及等效弹性模量的不一致，均会导致临界锚固长度有所差别。

（3）通过考虑锚杆剪应力分布不均匀性推导出锚杆合理锚固长度应在0． 5la左右，即合理锚固长度为临界锚固长度的一半，表达式为该式可用于指导工程实践，在保证锚杆承载力的条件下，使得锚杆得到充分利用，减少经济成本。