2020年高考数学全国I卷中显、隐性对称特征与启示
杨苍洲
(泉州第五中学,福建 泉州 362000)
2019 年7 月,在《中共中央国务院关于深化教育教学改革全面提高义务教育质量的意见》中,要求“坚持‘五育’并举,全面发展素质教育”.“五育”是指德育、智育、体育、美育、劳动教育,其中“美育”作为“五育”的重要组成部分,深刻地影响着了人类的生产生活.
作为义务教育的延伸,普通高中教育、高考同样也关注着“五育”.2020 年高考数学全国卷试题特点之一也是坚持立德树人,倡导“五育”并举,关注数学文化育人的价值,重视全面育人的要求,发挥数学科高考在深化中学课程改革、全面提高教育质量上的引导作用,其中之一体现为美育.
古希腊数学家普洛克拉斯有一句名言:“哪里有数学,哪里就有美”.“对称”是数学美的重要特征,让我们细品2020 年高考数学全国卷试题的对称美.
一、对称美在试题中主要表现
纵观全卷,“对称”在整卷中考查之多令人惊讶.有数式的对称,也有图形的对称;有整体的对称,也有局部的对称;有显性的对称,也有隐性的对称;有试题表征的对称,也有试题背景的对称;有对称所呈现的视觉享受,也有对称思想的解题应用.
(一)数式的对称美
数与式的对称美,主要是体现在等式或不等式的结构对称上,式子中的数字、字母可交换,结构匀称、和谐,令人赏心悦目.
1.数式的显性对称
题1(2020 年全国I 卷理)(x+)(x+y)5的展开式中x3y3的系数为
A.5 B.10 C.15 D.20
由(x+,因此要求展开式中x3y3的系数,即求(x2+y2)(x+y)5展开式中x4y3的系数.从不对称结构到对称结构的转化,也由此找到了解题的一个方向.
题2(2020 年全国I 卷文理)在直角坐标系xOy中,曲线C1的参数方程为(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为4pcosθ-16psinθ+3=0.
(1)当k=1 时,C1是什么曲线?
(2)当k=4 时,求C1与C2的公共点的直角坐标.
题中(1)(2)分别取k=1 和k=4.当k=1 时,曲线C1的参数方程为(t为参数),利用sin2t+cos2t=1 消去参数t,得C1:x2+y2=1;当k=4 时,曲线C1的参数方程为(t为参数),利用sin2t+cos2t=1 消去参数t,得
无论是k=1 还是k=4,无论参数方程还是普通方程,无论数式的结构还是函数图象,曲线C1都呈现出完美的对称特征.
2.数式的隐性对称
题3(2020 年全国I 卷理)若z=1+i,则z2-2z=
本题的“对称”在哪里呢?实际上本题深深隐含着命题者的对称情结.由z2-2z|=|z(z-2) |=|(1+i)(-1+i) |,可得式中的1+i,-1+i为对称式,两式为对方的共轭的相反数.由此可看出命题者的对称情结,越简单的问题往往越能看出命题者潜意识里有意无意地对称意识.
题4(2020 年全国I 卷文)设向量a=(1,-1),b=(m+1,2m-4),若a⊥b,则m=.
由向量a=(1,-1),a⊥b,得向量b=(x,x),这就是题中“数式”的隐性对称.若向量a,b的始点在坐标原点,则a的终点落在直线y=-x(二四象限的角平分线)上,由a⊥b,可知b的终点落在直线y=x(一三象限的角平分线)上,这也可看出题中“图形”的隐性对称.
(二)图形的对称美
几何图形也好,函数图象也好,无不充斥着各种各样的对称性,可谓图图精彩.如,立体几何中的正棱锥、正棱柱、圆锥、圆柱、球;解析几何中的直线、圆、椭圆、双曲线、抛物线;函数性质中奇偶性、周期性、对称性.无论是题中呈现出的显性对称还是试题背景中的隐性对称,命题者都在尝试通过图形,让我们感受世界的对称之美.
1.图形的显性对称
题5(2020 年全国I 卷文理)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )

图1
题小点多,本题不仅考查空间几何体、空间想象能力、几何直观素养,同时承载着数学文化的考查.试题为我们呈现了一个形状近似为正四棱锥的美丽的金字塔,带我们感受历史长河中绚丽的人类文明,领略古人的智慧,感受文化的魅力.
题6(2020年全国I卷文)已知圆x2+y2-6x=0,过点(1,2)的直线被该圆所截得的弦的长度的最小值为( )
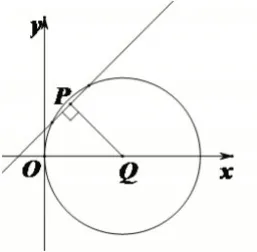
图2
A.1 B.2 C.3 D.4
古希腊数学家毕达哥拉斯曾经说过:“一切立体图形中最美的是球形,一切平面图形中最美的是圆形”.圆所展现出的对称美,常被赋予和谐、圆满、完美的寓意.本题中所呈现的圆x2+y2-6x=0,圆心Q在x轴上,当过点P(1,2)的直线l与PQ垂直时,直线l被圆Q所截得的弦长达到最小.不偏不倚地,此时的直线l关于PQ对称,点P为弦中点.
2.图形的隐性对称
题7(2020 年全国I 卷理)设a,b为单位向量,且|a+b|=1,则|a-b|=.
向量是具有大小和方向的量,可坐标运算也可几何运算,因此每道向量试题的背后往往有个美丽的图形支撑.本题中向量a,b,a+b,a-b恰构成菱形的边或对角线,又因为 |a|=|b|=|a+b|=1,所以该菱形恰由两个等边三角形或两个等腰三角形构成.图形结构对称,整洁简约,可以利用图象直接看出答案,实现速解、巧解,从而考查学生的画图、识图、用图能力.
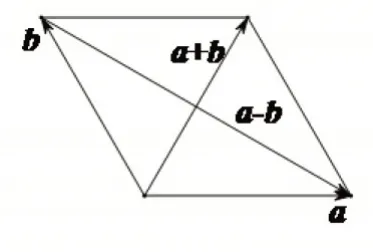
图3
题8(2020 年全国I 卷文)设F1,F2是双曲线C:x2-=1的两个焦点,O为坐标原点,点P在C上且|OP|=2,则△PF1F2的面积为( )
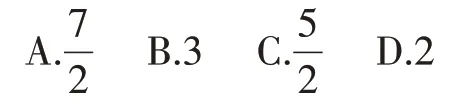
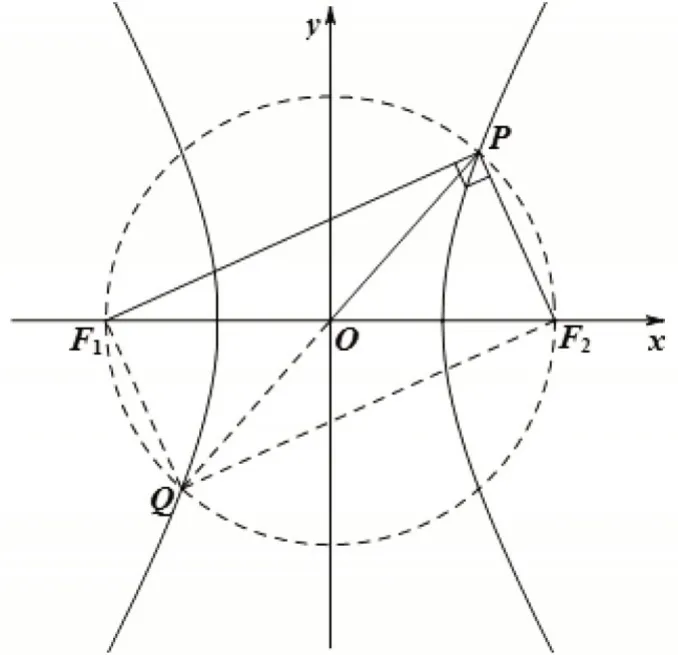
图4
二、对称思想的解题应用
对称性除了在视觉上给人以美的享受之外,也在思想上启迪解题者的灵感.上述数题以“显性对称”或“隐性对称”为背景的试题,基本都有丰富的解题思路,对称思想的作用发挥与否,为解题提供了不同的途径,不同的解题方法又有不同的解题速度和时间,当然,有对称意识的解题者,往往会在解题中占有一定的优势,从而缩短解题时间,体现出解题素养的差异.
(一)观察对称特征,常是解题入手点
对称特征常是知识背景的特殊特征.如三角函数的对称性,奇偶函数性的对称性,二次函数的对称性,圆、圆锥曲线的对称性等,都是解题中应观察到的重要信息.
题9(2020 年全国I 卷文理)设函数f(x)=cos(ωx+)在[-π,π]的图像大致如下图,则f(x)的最小正周期为( )
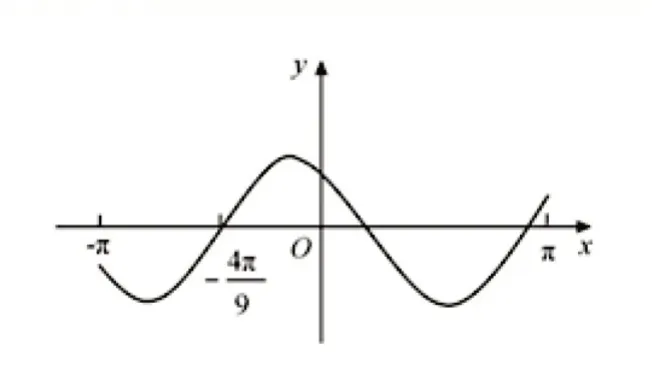
图5

由图可知π <T<2π,故k=0,T=对称特征是常见的审题观察点,也是解题关键点.翻译图象的对称特征,往往就能顺利解题.
(二)挖掘对称结构,可启迪解题思路
审题,一般需先观察题目的结构.“对称”或“不对称”是试题结构的一个重要特征,从该结构特征出发,往往是解题的思维着力点.
题10(2020 年全国I 卷理)若2a+log2a=4b+2 log4b,则
A.a>2bB.a<2bC.a>b2D.a<b2
等式2a+log2a=4b+2 log4b,可化为2a+log2a=22b+log2b.
我们观察到等式两边的结构是不对称的,恰是这样的“不对称”给了我们从“不对称”到“对称”转化的想法,此时,对称美的思想发挥了作用.从“不对称”到“对称”转化,也就给了我们从“等式”到“不等式”转化的机会,从而得到对称和谐的不等式,进而解决问题.
法一:因为b>0,故log2b<long22b.
又因为2a+log2a=22b+log2b,所以2a+log2a<22b+log22b.
考查函数f(x)=2x+log2x,f(x)在(0,+∞)单调递增,又f(a) <f(2b),所以a<2b.
法二:因为a>0,故log2a>log2.
又因为2a+log2a=22b+log2b,所以22b+log2b>2a+log2.
考查函数f(x)=2x+log2,则f(2b) >f(a),
又f(x)在(0,+∞)单调递增,所以a<2b.
实际上,本题还能作出如下推理:
因为a>0,b>0,故22b>2a,2a<22a.
又因为2a+log2a=a2b+log2b,所以2a+log2a>2b+log2b,22b+log2b<22a+log2a.
考查函数f(x)=2x+log2x,g(x)=22x+log2x,则f(a) >f(b),g(a) >g(b),
又f(x),g(x)在(0,+∞)单调递增,又所以a>b.
人人都有“向美”意识,化“不等称”为“对称”正是一种向着“对称美”的意识,“向美”让解题思路找到出路.
(三)欣赏对称之美,可优化解题途径
从美丽的对称结构中,发现数式、数形之间的内在联系,就能直接抓住问题的本质,也常常能另辟蹊径,使得问题得到快速解决.
题11(2020 年全国I 卷文)设{an}是等比数列,且a1+a2+a3=1,a2+a3+a4=2,则a6+a7+a8=( )
A.12 B.24 C.30 D.32
本题的常规解法,是化基本量进行解题.设等比数列{an}的公比为q,由a1+a2+a3=1,a2+a3+a4=2,得a1(1+q+q2)=1,a1(q+q2+q3)=2,解得q=2,a1=所以a6+a7+a8=a1)q5+q6+q7)=32.
常规方法利用的是“函数与方程”的思想,翻译条件得到含有q,a1的方程组,并解得q,a1,而后求解得a6+a7+a8的值.
我们再来观察题目的条件,题中式子a1+a2+a3,a2+a3+a4,a6+a7+a8所含的项数一样,且三项连续,式子匀称、和谐.解题者可以从对称结构中,找到一条解题的捷径.设等比数列{an}的公比为q,由此,我们发现a2+a3+a4=(a1+a2+a3)q,故q=2,所以a6+a7+a8=(a1+a2+a2)q5=32.由结构的对称,结合整体思想,把a1+a2+a2看成整体,就能简化运算,直接求出q=2 和a6+a7+a8的值.
(四)应用对称意识,可明确解题目标
圆锥曲线问题中有非常多的定点、定值性质.在探究探究定值、定点的位置时,由圆锥曲线的对称性,往往可以先猜后证,使得解题目标更加明确,解题方向更加明朗.
题12(2020 年全国I 卷文理)已知A,B分别为椭圆=1(a>1)的左、右顶点,G为E的上顶点,=8,P为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
(2)证明:直线CD过定点.
在问题(2)的求解过程中,由椭圆的对称性,可知,直线CD所过定点必在x轴上,因此只需写出直线CD的方程,并令y=0,求出的x的值,即为该定点的横坐标.

基于对称,先猜后证.猜测的结果,使得解题方向更加明确,有效地减小了思维的难度,从而更加坚定了解题信心.
三、结束语
对称美,是数学美的一种基本形式.2020 年高考数学全国I 卷,多处或有意或无意地考查了对称美.有些试题是命题者有针对性地检测考生对“对称美”的应用,可见高考对“对称”的重视;有些试题是命题者无意识地设置了“对称美”的隐性背景,实则是命题者潜意识里的对称意识.对称显示数学美的意境!
数学不缺少美,却常常缺少发现美的眼光.我国数学家华罗庚说过:“就数学本身而言,是壮丽多彩、千姿百态、引人入胜的……认为数学枯燥乏味的人,只是看到了数学的严谨性,而没有体会出数学的内在美.”正值国家大力提倡“五育并举”之机,数学教育理应担负起培养学生欣赏美的眼光、应用美的意识、创造美的能力之重任。

