统计试题得分低的原因与应对策略——以2020 年福建省质检理科第20 题为例

王淼生 黄 勇

（1.厦门第一中学，福建 厦门 361003；2.福建教育学院数学研修部，福建 福州 350025）

一、试题呈现

为贯彻落实党中央全面建设小康社会的战略部署，某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.截至2018 年年底，按照农村家庭人均年纯收入8000 元的小康标准，该地区仅剩部分家庭尚未实现小康.2019 年7 月，为估计该地区能否在2020 年全面实现小康，统计了该地区当时最贫困的一个家庭2019 年1 月至6 月的人均月纯收入，作出散点图如下：

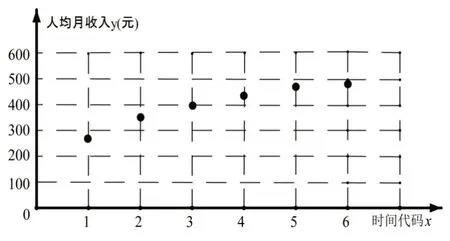
根据相关性分析，发现其家庭月纯收入y与时间代码x之间具有较强的线性相关关系（记2019 年1 月，2 月…分别为x=1，x=2，…，以此类推），由此估计该家庭2020 年能实现小康生活.但2020 年1 月突如其来的新冠肺炎影响了奔小康的进展，该家庭2020 年第一季度每月的人均纯收入只有2019 年12 月的预估值的（I）求该家庭2020 年3 月份的人均月纯收入；

（II）如果以该家庭3 月份人均月纯收入为基数，以后每月的增长率为a，为使该家庭2020 年能实现小康生活，a至少应为多少？（结果保留两位小数）

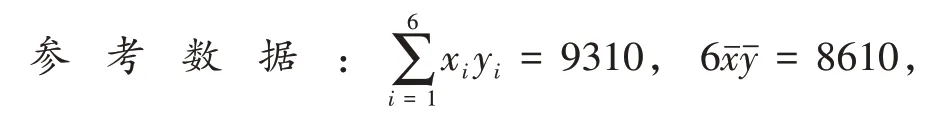
二、命题宗旨

本题是一道典型的统计综合试题，主要考查线性回归方程、等比数列（通项与求和）、函数单调性（导数应用）及不等式求解等基础知识.渗透方程与函数、转化与化归、分类与讨论及数形结合等数学思想.考察抽象概括、推理论证、运算求解及数据处理等能力，尤其应用数学知识解决实际问题的能力.培养数学抽象、逻辑推理、数学建模、数学运算及数据分析等核心素养.

三、规范解答

（一）对于（I）来说

相关数据代入上述公式得到

（二）对于（II）来说

设该家庭2020 年人均月纯收入为数列{an}（n=1,2,3,…,12），则a1=a2=a3=500.依题意可知从3 月份起该家庭人均月纯收入构成以a3=500 为首项、公比为1+a的等比数列.要使该家庭2020 年能够实现小康生活，则需要满足：

因“结果保留两位小数”，同时要满足实际问题，故a≥0.08，即以后每月增长率为8%，该家庭2020 年才能实现小康生活.

注：以上为笔者的详细解答过程.命题专家提供的参考答案中没有呈现（1）中的论证过程，而是直接列出算式：f(a)≥f(0.15)=(1+0.15)10-14 × 0.15-1 ＞0，这显然不够严谨.严谨性是数学的最重要特征，尤其解答题更是如此.

四、剖析得分率低的原因

近年来，统计（或概率统计）综合题是考试的热点、重点、难点，并有逐年加大考查力度的趋势.这类试题不仅文字篇幅较长、信息含量很大、符号图表密集，而且阅读理解困难、运算过程复杂、参考数据冗长、参考公式繁杂，不少考生害怕甚至放弃.数据表明本题得分率较低（本题满分12 分，以厦门地区为例，全市均分2.4 分）.为何得分如此之低？问题症结原因何在？

（一）盲目讲题，轻视阅读

不少教师急于解题，追求短、平、快节奏，没有培养学生阅读的意识.学生连基本题意都不清楚，教师就已经开始滔滔不绝，学生云里雾里，不知所措.教师应该首先引领学生阅读，尤其关注核心词.比如本题中小康标准、家庭人均年纯收入、家庭人均月纯收入、散点图、时间代码、线性相关关系、预估值、增长率、保留小数、参考数据及参考公式等.

（二）依赖课件，轻视板书

毋庸置疑，多媒体（课件、投影、视频、音频等）确实为数学教学带来了不可或缺的作用.但是一味地依赖课件，一闪而过，也是导致学生难以深入领悟统计试题的因素.教师应该将整个运算过程清晰地板书在黑板上，甚至有些关键环节，还需要给予特写“镜头”.只有这样，学生才能有充足的时间、足够的空间，用眼观看，用手操练，用心琢磨.

（三）追求数量，轻视质量

为了抢进度、赶速度，不少教师一节课动辄讲解5～6 道统计（或概率）综合试题，更有甚者一口气讲9～10 道，这种一味追求数量的蜻蜓点水式解题教学，教师看似口若悬河、滔滔不绝，课堂似乎此起彼伏、热闹非凡，学生实则收效甚微，甚至一无所获.倒不如踏踏实实讲解1 道或2 道试题，效果更好.

（四）浮于表面，轻视抽象

史宁中教授认为，通过抽象，人们把现实世界中与数学相关的东西抽象到数学内部，形成数学的研究对象.统计试题贴近生活，需要教师在适度去生活化、去情景化的过程中实现数学抽象，回归数学本质，这是解决统计（概率）问题的必由之路.让学生感悟数学的抽象过程，体会具体与抽象之间的差异，积累从具体到抽象的数学活动经验，形成数学抽象素养.缺少抽象，浮于表面，机械套用公式解题没有价值.

（五）只顾计算，轻视运算

不少教师以为统计题就是加减乘除、乘方开方等数学计算而已.其实，统计学更多的是数学运算.一字之差，天壤之别.数学运算历来是课程和教学的重点内容.数学运算并不仅仅是数学计算，也不能理解为一般的数学计算.这就是为何课标［1］将数学运算作为六大核心素养之一，而不是数学计算.数学运算是在理解运算对象基础上，掌握运算法则，探究运算方向，选择运算方法，实施运算流程，最后才能求得运算结果.

（六）关注结果，轻视建模

在抽象的基础上，用数学语言表达问题，用数学知识、数学方法分析并解决问题.统计题源于生活，需要建立恰当的数学模型.数学建模过程主要包括：在实际情景中从数学视角发现问题、提出问题，分析问题、建立模型，计算求解，检验结果、改进模型，最终解决实际问题.教师没有向学生充分展示建模过程及数学模型，求解就犹如空中楼阁、海市蜃楼.

五、应对策略

章建跃博士在其文中忧心忡忡地警示：“通过调查研究以及收集的数据统计结果表明，纵使是处于金字塔顶部的重点高中数学教师，他们的概率统计知识储备严重不足，80%以上的教师对大部分概率统计基本概念的认识都处于模糊状态，理解深度不够，缺乏用这些概念答疑解惑的能力，影响概率统计知识的教学效果.”［2］

对于一线教师，要想达到深度理解概率统计基本概念的境界，绝非一朝一夕，还需从长计议，逐步提高.但是，至少目前可以在强化阅读、落实细节、渗透思想、培养素养，尤其在恢复心态等方面做得更好一些.

（一）强化阅读

教师要有意识地培养学生良好的阅读习惯，遵循通读（整体浏览、了解概况：统计模块、线性回归、数列求和等）→深读（把握方向、构建框架：“出场”顺序、推导公式、运算求解）→精读（关键信息、抽象概括、精准建模）流程.对于有些试题，甚至需要多次通读→深读→精读，达到螺旋上升.其中关键在于精读，以本题为例，精读包括：

1.读懂“散点图”信息：依据2019 年1 月至6 月的人均月纯收入作出，散点图仅仅精准看出x而不能得到y的确定值，如何求解呢？

2.清楚“小康标准”含义：农村家庭人均年纯收入8000 元，也就是说12 个月中每个月的纯收入之和不小于8000 元，如何计算呢？

3.明确“时间代码”意义：2019 年1 月，2 月…分别为x=1，x=2，…，以此类推.2020 年3 月份的人均月纯收入可以看作x=15 对应的预估值吗？

4.理解“线性相关”关系：家庭月纯收入y与时间代码x之间具有较强的线性相关关系，也就是说需要依据散点图求出线性回归方程，如何求解呢？

6.使用“参考数据”时机：为何列出一连串的参考数据？如何使用这些参考数据？何时使用这些参考数据？这些参考数据仅仅用于计算吗？对探究运算方向有何引领作用？为数学建模做了何种铺垫呢？

（二）落实细节

“细节决定成败.”与其狂轰乱炸，倒不如讲透一道试题更有效.笔者整整花了一节课才把此题讲解清楚.那本题该如何讲评呢？

1.“出场”顺序——求解线性回归方程是一个“组装”过程求解回归直线是多种“零配件”“组装”过程.既然“组装”，就应该安排好“零配件”“出场”顺序.如何确定与“出场”次序呢？为何首先需要求出与？如何求？怎样得到？涉及的公式有几个？本题借助哪个公式才能求？提供的公式是否能够求出？如何推导另一个公式求？两个公式有何差异？的含义是什么？的作用是什么？求出目的何在？笔者阅卷发现，绝大部分学生东一榔头西一棒，缺胳膊少腿现象普遍存在.

2.善待公式——借力参考公式是确定运算方向的摸索过程

命题专家为何给出参考公式：(1+a)n≈1+？这个参考公式有何作用？为何不直接使用学生熟悉的二项式定理而专门给出这个参考公式？目的何在？可以不“搭理”这个参考公式而直接使用二项式定理吗？为何给出限制条件：n≥10？限制条件：|a|＜0.15 意味着什么？如何创造“机会”靠近这个条件？这个参考公式为后续运算指点了什么方向？怎样使用这个参考公式？何时使用这个参考公式？笔者阅卷发现，绝大部分学生不善于或根本不会使用这个参考公式，导致前功尽弃.

3.回归实际——寻求增长率是“多兵种”数学建模过程

统计学就是研究如何搜集、整理、分析生产、生活中的数据以及由数据分析结果作出科学决策.增长率a意味着什么？建立何种数学模型？等比数列公比q与增长率有何关联？为何a=1+a而不是q=a？等比数列首项为何不是a1而是a3？求解结果如何回归实际问题？如何满足实际问题？笔者阅卷发现，纵使少数学生计算得到a≥0.07，纯粹从纯数学“四舍五入”而没有兼顾实际问题来处理“结果保留两位小数”，导致最后增长率是7%而不是8%.

（三）渗透思想

数学思想是数学灵魂，是数学知识在更高层次上的抽象和概括，是知识转化为能力的桥梁，它对学生认知结构的发展起着重要作用.本题渗透了方程与函数、转化与化归及数形结合等数学思想，尤其分类与讨论思想.分类与讨论思想大致分为两类，一类是数学概念自身需要分类，比如指数、对数的底数a分a＞1 及0 ＜a＜1，等等.这类是常见的，学生基本掌握.另一类则是因为运算或者化简需要，这一类往往与运算对象、方法选择有关，并常常为数学运算指明方向.比如，面对高次（10 次）不等式①：(1+a)10-14a-1≥0，必须降次.如何降次？如果采用学生熟悉的二项式定理展开，其本质仍然还是高次（10 次），于是只能寻求命题专家给出的参考公式：(1+a)n≈1+.能够直接利用这个参考公式吗？不能！为什么？因为首先要满足使用公式的先决条件：|a|＜0.15，于是顺理成章地进行分类：|a|＜0.15 及|a|≥0.15.这类分类讨论在统计（概率）综合试题的运算中体现得淋漓尽致.

（四）培养素养

统计（概率）试题综合考查学生用数学眼光观察问题、用数学思维分析问题、用数学语言表达问题、用数学知识解决问题的绝佳素材，是全面落实立德树人、发展素质教育的具体案例，是优化数学思维品质、培养数学学科核心素养的典范，这正是近年来统计（概率）试题成为高考热点、重点的缘由，更是逐年加大考查力度的依据.以本题为例，数学建模（等比数列、构造函数等）；数据分析（保留小数、回归实际等）；数学运算（等比求和、解不等式等）；逻辑推理（证明递增函数、推导公式等）；直观想象（由图思数：散点图；从数想式：由参考数据：≈62.81，联想到一元二次方程（或不等式）的判别式）.其中，数学抽象则贯穿于数学建模、逻辑推理、数学运算、数据分析及直观想象整个过程.

（五）恢复心态

客观地讲，本题并非新题，只是重新包装而已，这类试题比比皆是，如2015 年全国卷I 理科第19 题与本题极其相似.其实，本题难度并不是很大，为何得分率如此之低？笔者通过问卷调查发现，不少学生心里害怕统计试题，看到大量文字、符号、图表就直接放弃，这也是造成得分极低的关键原因.长期以来，学生屡考屡错，教师屡错屡讲；学生一错再错，教师大讲特讲，形成怪圈：错了再讲，讲了再考，再考又错，错了再考.教师疲于讲解，学生被动应付.“心态决定一切.”学生长期堆积起来的厌烦心情、害怕心理、逃避心态，急切需要教师和风细雨地促膝沟通，急切需要情真意切地心灵安抚，急切需要教师踏踏实实地细腻讲解，率领学生一点一点、一步一步、一次一次地走出困境.随着教师教学策略的优化、专业素养的提升，随着学生心态的调整、信心的恢复，相信学生一定能够敢于正视统计试题，善于解决统计试题.