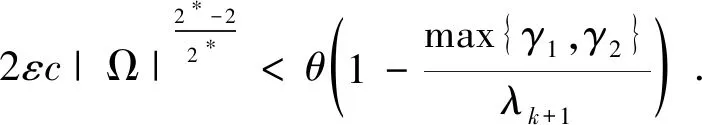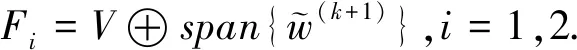一类带临界指数的分数阶Laplacian方程组解的存在性

史芳芳，叶国菊，刘尉，赵大方

(河海大学理学院， 江苏 南京 210098)

0 引言

分数阶偏微分方程具有重要的理论意义和丰富的应用背景，与泛函分析、数理金融、微分几何、物理学等分支有着十分紧密的联系．近年来，临界非线性椭圆方程受到了广泛的关注．分数阶Laplacian算子在科学及工程领域有着重要的应用，如优化问题、障碍问题、金融及相变理论等[1-2]．因此,分数阶Laplacian方程组解的存在性问题的研究是一项非常有意义的工作，已经成为非线性分析领域的热门研究方向之一．

关于带临界指数的分数阶Laplacian方程解的存在性问题的研究有很多．2015年，Mdica和Servadei[1]研究了临界方程

在λ∈(0,λ1)时非平凡解的存在性，其中λ1表示带Dirichlet边界条件的非局部算子Lk的第一个特征值．Liu[4]将文献[3]中的结果推广到了方程组上．在文献[5]中，Servadei通过引入合适的最佳分数阶临界常数Sk对文献[3]中的结果进行了推广，得到了当λ∈(0,∞)时非平凡解的存在性．受文献[3-5]的启发，笔者将文献[5]中的结果推广到了下列带临界指数的分数阶Laplacian方程组

(1)

其中，s∈(0,1),Ω⊂n是具有连续边界的有界开集，是分数阶临界Sobolev指数，函数G(x,u,v)是临界耦合项的一个低阶扰动项.Lk与文献[5]中定义一样，是一般的非局部微积分算子，其表现形式为

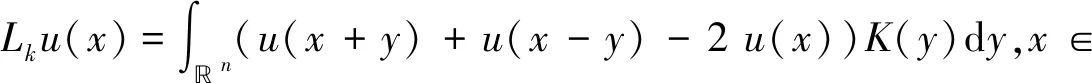
其中函数K:n→(0,+∞)称为算子Lk核，并且满足：

K1)mK∈L1(n),其中m(x)=min{1,|x|2}；

K3)K(-x)=K(x),x∈n{0}．

受文献[4-5]的启发，我们假设低阶扰动项G:Ω××→满足以下条件：

G4)Gs(x,s,t)≥0,Gt(x,s,t)≥0,a.e.x∈Ω,s,t∈；

注1当问题(1)中的v≡0时，就退化为文献[5]中讨论的问题.

我们记Dk(Ω)={f∈X:f=0a.e.nΩ}，这里X是Lebesgue可测函数构成的线性空间.

在Dk(Ω)上定义内积：

并且由这个内积产生的范数为

(2)

在本文中,{λk}k∈N表示带齐次Dirichlet边界条件的算子Lk的特征值序列，满足：

{ek}k∈N是对应于λk的特征函数列．将{ek}k∈N标准正交化后得到L2(Ω)中的标准正交基且是Dk(Ω)中的正交基．为方便起见，我们仍记作{ek}k∈N．最佳分数阶Sobolev常数Sk,γ1,γ2定义为：

本研究目的是研究方程组(1)式非平凡弱解的存在性，即以下问题的非平凡解的存在性：

定义1任意s∈(0,1),任取试验函数(φ,φ)∈Dk(Ω),若存在(u,v)∈Dk(Ω)使得

(3)

则称(u,v)是问题(1)的弱解.

为寻找问题(1)式的一个弱解(u,v)，我们考虑(3)式对应的一个能量泛函Ek:Dk(Ω)→，即

显然Ek在空间C1(Dk(Ω),)上有定义且泛函Ek的临界点就是(3)式的非平凡解，即问题(1)的弱解.

本文中的主要结果如下：

定理1设s∈(0,1),n>2s,Ω⊂n是带有连续边界的有界开集．设函数K:n{0}→(0,+∞)是满足条件K1)～K3)函数G:Ω××→是满足条件G1)～G5)．最后，假设存在(u0,v0)∈Dk(Ω)(0,0),u0,v0≥0a.e.于n使得Sk,γ1,γ2(u,v)

其中i=1时,w=u0；否则w=v0.

那么，对∀γ1,γ2>0，问题(3)式有一个非平凡解(u,v)∈Dk(Ω).

注2当问题(1)中的v≡0时，定理1就退化为文献[3]中的主要结果；当γi∈(0,λ1)时就退化为文献[2]中的主要结果，因此本文中只证明当γi∈[λk,λk+1),k∈N时的情形.

1 预备知识

引理1[5](环绕定理) 设E=V⊕X是实Banach空间，V是有限维的．假设泛函I∈C1(E,)满足(PS)条件且：

I1)存在常数ρ,α>0,使得I∣∂Bp∩X≥α；

令

那么，c是泛函I有一个临界点，且c≥α．其中(PS)条件的定义如下：

设E=V⊕X是实Banach空间,V是有限维的，泛函I∈C1(E,)．如果对任意序列{uk}⊂E满足：

i)I(uk)有界；

ii)I′(uk)→0,k→∞；

序列{uk}在E中都有强收敛子列，则称泛函I满足Palais-Smale条件(简称为(PS)条件)，序列{uk}被称为(PS)序列．

引理2[2]设函数G:Ω××→满足条件G1)～G5)．那么，对任意的ε>0，存在a(ε)>0和b(ε)>0使得对a.e.x∈Ω，任意的s,t∈有

|G(x,s,t)|≤ε(|s|2*+|t|2*)+a(ε)(|s|+|t|),

|G(x,s,t)|≤ε(|s|2+|t|2)+b(ε)(|s|2*+|t|2*)．

引理3[2]若序列{(un,vn)}满足

Ek(un,vn)→c,Ek′(un,vn)→0,n→∞，

这里c>0是仅依赖n和s的常数，则序列{(un,vn)}在D(Ω)中有界．

引理4[7]设函数K:n{0}→(0,∞)满足条件K1)～K3)，那么

这里c>0是仅依赖n和s的常数．

2 主要结果的证明

将经典临界情况下的变分法和拓扑度方法应用于非局部分数阶情形，得到定理1的证明．首先，我们证明泛函Ek满足(PS)条件：

命题1设γ1,γ2∈[λk,λk+1),k∈函数G满足条件G1)～G5)．设c∈满足

(4)

若Dk(Ω)中的序列{(un,vn)}满足：

Ek(un,vn)→c

(5)

sup{|〈Ek′(un,vn),(φ,φ)〉|:(φ,φ)∈Dk(Ω),‖(φ,φ)‖Dk(Ω)=1}→0,n→∞

(6)

则存在(u∞,v∞)∈Dk(Ω)使得‖(un,vn)-(u∞,v∞)‖Dk(Ω)→0,n→∞．

命题1的证明由引理3知{(un,vn)}在Dk(Ω)中有界并且问题(3)有一个解(u∞,v∞)∈Dk(Ω)．取(3)式的试验函数(φ,φ)=(u∞,v∞)，从而有

Gv(x,u∞(x),v∞(x))v∞(x)dx，

因此，由条件G1)知

0

(7)

由于{un},{vn}在L2*(n)中有界以及L2*(n)是自反空间，有

un⇀u∞,un⇀u∞于L2*(n)

(8)

un→u∞,un→u∞于Lυ(n)

(9)

un→u∞,un→u∞a.e.于n

(10)

由Brezis-Lieb引理有

(11)

及

(12)

接下来，我们证明

(13)

由于un,vn在L2*(Ω)中有界，则存在k>0使得

(14)

(15)

那么，由Sobolev嵌入定理可知

G(·,un(·),vn(·))∈L1(Ω)．

|Ω′|≤η(δ)

(16)

利用Hölder不等式以及(14)～(16)式，有

故G(·,un(·),vn(·))在Ω中是一致可积的．

又G(·,un(·),vn(·))→G(·,u∞(·),v∞(·)),a.e.n→∞，因此(13)式成立．

进一步，利用引理2和Vitali收敛定理，这里与(13)式的证明一致，类似地有

由(10)式以及G(x,u,v)关于u和v是超线性的可知，映射t→Gu(x,t,v)和s→Gv(x,u,s)在中是连续的，因此

(17)

从而由(10)式，有

(18)

根据Ek的定义、(9)式、(11)～(13)式，有

(19)

由于(8)式和(12)式成立，所以

μ2(|vn(x)|2*-2vn(x)-|v∞(x)|2*-2v∞(x))(vn(x)-v∞(x))dx=

(20)

从而由(6)式，易得

o(1)=〈Ek′(un,vn),(un,vn)-(u∞,v∞)〉=

〈Ek′(un,vn)-Ek′(u∞,v∞),(un,vn)-(u∞,v∞)〉,n→∞

(21)

另一方面，由(9)式、(17)、(18)式及(21)、(22)式，有

〈Ek′(un,vn)-Ek′(u∞,v∞),(un,vn)-(u∞,v∞)〉=

(22)

因此，由(21)、(22)式得

(23)

现在，我们可以总结命题1的证明．由(23)式易知，

由(11)式和(19)式，我们有

(24)

注意到，序列{(un,vn)}在中有界．从而存在一个子序列，我们仍记为{(un,vn)}，从而由(23)式有

(25)

显然L≥0．此外，由Sk的定义，我们有

这与(4)式矛盾. 因此L=0，即

故泛函Ek满足(PS)条件．

接下来，我们证明泛函Ek具有引理1所需要的几何特征．

命题2设γi∈[λk,λk+1),i=1,2;k∈N，函数G满足条件G1)～G5)．那么，存在ρ>0,β>0，使得对任意的(u,v)∈Pk+1×Pk+1,‖(u,v)‖Dk(Ω)=ρ时，有Ek(u,v)≥β．

命题2的证明设(u,v)∈Pk+1×Pk+1, 由引理2、条件K2)及引理4有

由于2*>2，选择充分小的ρ，满足1-kρ2*-2>0，从而由假设得

即命题2得证．

命题3设γi∈[λk,λk+1),i=1,2.k∈，函数G满足条件G1)～G5)．那么对任意的u,v∈span{e1,…,ek}，有Ek(u,v)≤0．

命题3的证明设u,v∈span{e1,…,ek}，那么，存在ui,vi∈,i=1,…,k，使得

由于{e1,…,ek}是L2(Ω)中的标准正交基，则有

(26)

(27)

那么，由(26)、(27)式及文献[6,命题9-(b)、(e)]知ei∈Dk(Ω),∀i∈N，有

由于λi≤λk≤γ1,γ2,i=1,2,…，k．因此Ek(u,v)≤0．即命题3得证．

命题4设γ1,γ2≥0，函数G满足条件G1)～G5)，F1,F2是Dk(Ω)的有限维子空间．那么，存在R>ρ，使得对任意的(u,v)∈F1×F2，当‖(u,v)‖Dk(Ω)≥R时，有Ek(u,v)≤0．这里的ρ是命题2中给定的．

命题4的证明设(u,v)∈F1×F2，因为γ1,γ2≥0且Gu(x,u,v)≥0,Gv(x,u,v)≥0，那么

这里k是某一常数．由2*>2知，当‖(u,v)‖Dk(Ω)→+∞时，有Ek(u,v)→-∞．

即命题4得证．

因此，由命题2～4知泛函Ek具有引理1所需要的几何特征．最后我们验证Ek满足环绕临界水平低于满足(PS)条件的阈值．我们令

注意到V是有限维的，则由文献[6,命题9-(f)]知V⊕PK+1=Dk(Ω)．此外，由命题2～4得，存在R>ρ>0,β>0，使得

Ek(u,v)≥β>0,u,v∈PK+1且‖(u,v)‖Dk(Ω)=ρ>0；

Ek(u,v)≤0,u,v∈V；

Ek(u,v)≤0,u∈F1,v∈F2且‖(u,v)‖Dk(Ω)≥R；

因此，Ek的几何结构满足引理1的条件I1)和I2)以及文献[5, 备注5.5-(iii)]．Ek的环绕临界水平cL的定义如下：

其中

由cL的定义知, 对任意的h∈,

进而, 由Fi是线性空间有

因此

cL≤max(u,v)∈Q1×Q2Ek(u,v)≤

由Gu(x,u,v)≥0,Gv(x,u,v)≥0a.e.x∈Ω,u,v∈以及文献[1,命题20]，有

即证得Ek满足环绕临界水平低于满足(PS)条件的阈值.

综上, 由引理2可知, 定理1的结论成立.