含智能提示限速的全速度差模型的稳定性和孤立波
曹 芳,化存才
(云南师范大学 数学学院,云南 昆明 650500)
多年来,城市交通车辆不断暴增,使得交通拥堵、环境污染、能源浪费等问题日益严重,且成为难以解决的城市交通科学问题.因此,解决城市交通拥堵是学者们和城市管理者密切关注的重要问题.
研究交通拥堵问题的基础是经典的车辆跟驰模型.跟驰模型最早由Pipes[1]提出,1961年,Newell[2]对Pipes的模型进行了改进.1995年,Bando[3]为改进[2]中的模型产生的无限大加速度而提出了最优速度(optimal velocity, OV)模型,但是,后来发现此模型也存在加速度过大和不切实际减速的问题.为解决这个问题,Helbing等[4]提出了考虑正速度差的广义力(generalized force, GF)模型.2001年,姜锐等[5]同时考虑正负速度差而提出了全速度差(full velocity difference model, FVD)模型.2006年,王涛等[6]考虑了多辆前车速度差的信息而提出了多速度差(multiple velocity difference, MVD)模型.近年来,随着智能交通系统ITS的新发展,有很多学者通过改进一些经典的跟驰模型[7-20],使其有助于研究和解决交通问题.
本文将在全速度差模型(FVD)基础上,考虑智能提示限速信息,给出改进的FVD模型,即含有智能提示限速信息的FVD模型,分析其稳定性条件和精准稳定条件,以及不同区域内的孤立波.
1 考虑限速提示信息的全速度差模型
在智能交通系统提供交通信息服务的环境下,驾驶员可以得到智能提示限速信息,从而能及时调整行驶车速,以保障交通稳定.本章主要考虑智能系统提前td时间提示限速信息,基于在本车与前车之间的全速度差模型,引入如下的跟驰模型:
(1)
其中,a是驾驶员的敏感系数,V(Δxn(t))是优化速度函数.Δvn(t)=vn+1(t)-vn(t)是前后两辆车的速度差,λ表示驾驶员对前车相对速度的反应系数.γ>0表示有智能提示限速后驾驶员的反应系数.td是驾驶员提前获知限速信息的时间.
2 模型(1)的线性稳定性条件
为便于后面的计算,现将模型(1)式改写成下面的形式:
(2)
设初始状态是稳定态,车流的车头间距都是b,相应的优化速度是V(b).此时稳态交通流的车辆位置可表示为
(3)
现加1个小扰动,即
yn(t)=exp(ikn+zt).
(4)
有:
(5)
将(5)式代入(2)式得到:
(6)
其中Δyn(t)=yn+1(t)-yn(t).将(6)式Taylor展开得:
(7)
z2=a[V′(b)(eik-1)-z]+λz(eik-1)+γz[eztd-1].
(8)
再令
(9)
代入(8)式中,得:
(10)
将z=z1ik+z2(ik)2+…,代入(10)式,得到模型(1)的结果:
(11)
当z2<0时,交通流将不稳定;当z2>0时,交通流的稳定状态不变.于是,我们得到模型(1)的如下临界稳定条件:
a=2(1-γtd)V′(b)-2λ.
(12)
当满足如下条件时,交通系统将处于不稳状态:
a<2(1-γtd)V′(b)-2λ,
(13)
当满足如下条件时,交通系统将处于稳定状态:
a>2(1-γtd)V′(b)-2λ.
(14)
选取模型(1)的优化速度函数如下:
(15)
取参数值vmax=3,hc=4,λ=0.3.在图1中分别给出了FVD模型与改进模型(1)在取td和γ不同值时的临界曲线,位于临界曲线外的区域是稳定的,位于临界曲线内的区域是不稳的.从图1中可以直观地看出改进模型(1)的稳定区域比FVD模型扩大.事实上,因成立着2V′(b)-2λ>2(1-γtd)V′(b)-2λ,而a>2V′(b)-2λ为FVD模型的稳定性条件,故这表明含智能提示限速信息能有效缓解交通流拥堵现象.
下面,我们就3种智能提示限速情况,对稳定条件(14)作进一步的精准分析.
(i) 如驾驶员对限速度vM反应快,则可设γ与vM成正比,即取γ=kvM.此时有γtd=kvMtd=ksM0,其中sM0为车辆在td时间内按限速度行驶的距离,于是,稳定条件(14)变为:a>2(1-ksM0)V′(b)-2λ.由此可知,提前提示限速的时间td越长,相应的车辆行驶的距离sM0就越远,交通流就会越稳定.

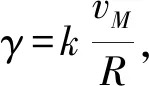
3 模型(1)的非线性分析和孤立波
模型(1)的孤立波解反映了由密度波极限状态表示的交通拥堵现象.本节通过约化摄动法,从模型(1)导出相应于不同的区域的非线性波方程及其孤立波解.
为了方便计算,我们先将模型(1)改写为:
(16)
3.1 在稳定区域导出Burgers方程和孤立波解
在稳定区域,条件(14)成立.现对空间变量n和时间变量t引入1个缓慢变量:
X=ε(n+bt),T=ε2t,
(17)
其中0<ε≪1,b为待定参数.设车头间距为:
Δxn(t)=h+εR(X,T).
(18)
将(17)、(18)代入(16),并将其Taylor展开至ε3,得到如下方程:
(19)
令b=V′(h)消去ε2,方程(19)化为:
(20)

(21)
3.2 在亚稳定区域导出KdV方程和孤立波解
在亚稳定区域,条件(12)成立.取:
X=ε(n+bt),T=ε3t,
(22)
参数意义同上,设车头距为:
Δxn(t)=h+ε2R(X,T).
(23)
将(22)、(23)代入(16),将其Taylor展开至ε6,得如下方程:
(24)
令b=V′(h)消去ε3,在临界稳定线as=2V′(h)(1-γtd)-2λ附近,令a=(1+ε2)as,则(24)式可化为:
(25)
其中,
(26)

(27)
从(27)可知,A越大时,车辆的间距越大,交通流会更加稳定,从而可避免拥堵的发生.在其他条件不变,td越小时,车辆的间距越大,因而交通流稳定.
3.3 在不稳定区域导出mKdV方程和孤立波解
在不稳定区域,条件(13)成立.考虑临界点(hc,ac)附近,取:
X=ε(n+bt),T=ε3t,
(28)
且间距为:
Δxn(t)=hc+εR(X,T).
(29)
将(28)、(29)代入(16), Taylor展开至ε5,得到方程:
(30)
令b=V′(hc),a=(1+ε2)ac.则(30)化为:
(31)
其中,
(32)
忽略O(ε)项,方程是mKdV方程.于是:
(33)
其中传播速度为c=5g2g3/(2g2g4-3g1g5).
于是得到:
(34)
于是得到扭结-反扭结波解的振幅A为:
(35)
扭结-反扭结波解代表了模型运动中的共存相,包括低密度的自由运动相和高密度的拥挤相,自由运动相和拥挤相的车头距分别是Δxn(t)=hc+A和Δxn(t)=hc-A.
4 结语
本文主要研究智能提示限速信息对于交通流的影响问题,引入了含有智能提示限速信息的全速度差模型,导出和分析了模型的稳定性条件和孤立波解.稳定性条件表明,相比于FVD模型,考虑智能限速信息提示能扩大交通流的稳定区域;进而根据驾驶员对智能提示限速度的反应快、慢及有弯道等3种情形,对稳定条件作了精准分析,使阐释结果更加符合现实交通情形.通过非线性分析得到了Burgers方程、KdV方程和mKdV方程,并且分别求得其孤立波解.

