等效电压源定理在电路分析中的应用

摘 要:“等效法”是高中处理电学问题的常用方法,本文结合几个常见的电路,利用“等效法”的理论等效电压源定理与其他方法对比分析,体现等效电压源定理简单快捷的特点.
关键词:等效;电压源;多电源
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2020)10-0073-02
收稿日期:2020-01-05
作者简介:徐仁杰(1989.10-),男,硕士,中学二级教师,从事中学物理教学研究.
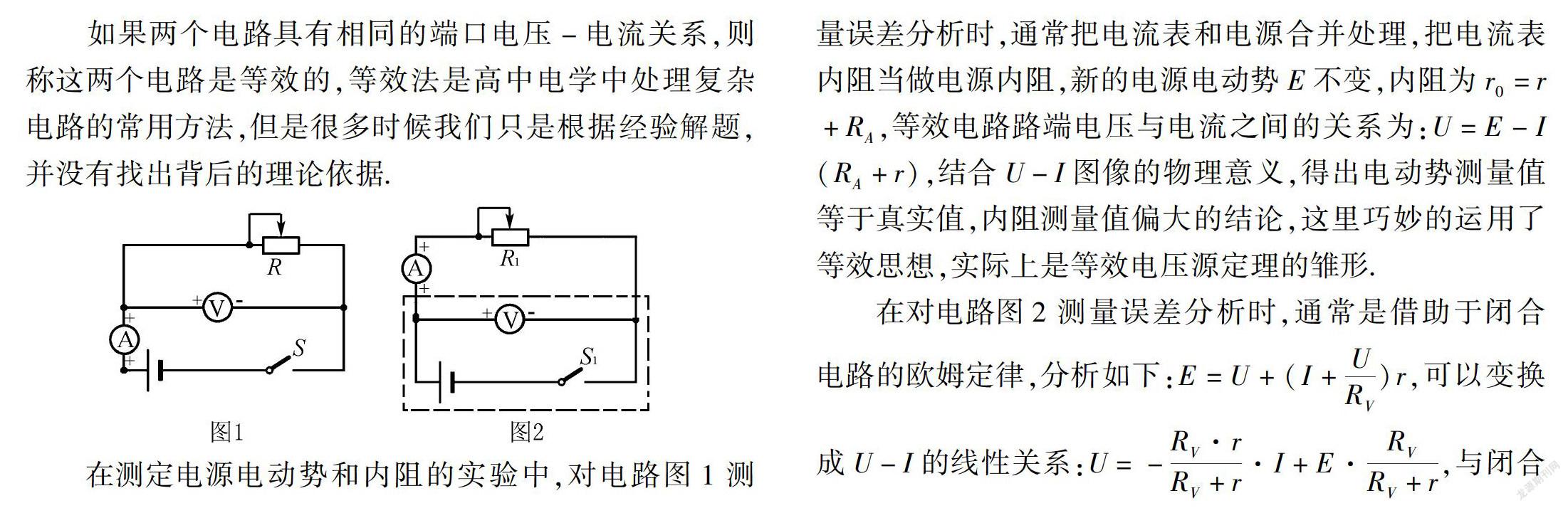
如果两个电路具有相同的端口电压-电流关系,则称这两个电路是等效的,等效法是高中电学中处理复杂电路的常用方法,但是很多时候我们只是根据经验解题,并没有找出背后的理论依据.
在测定电源电动势和内阻的实验中,对电路图1测量误差分析时,通常把电流表和电源合并处理,把电流表内阻当做电源内阻,新的电源电动势E不变,内阻为r0=r+RA,等效电路路端电压与电流之间的关系为:U=E-I(RA+r),结合U-I图像的物理意义,得出电动势测量值等于真实值,内阻测量值偏大的结论,这里巧妙的运用了等效思想,实际上是等效电压源定理的雏形.
在对电路图2测量误差分析时,通常是借助于闭合电路的欧姆定律,分析如下:E=U+(I+URV)r,可以变换成U-I的线性关系:U=-RV·rRV+r·I+E·RVRV+r,与闭合电路的欧姆定律对比会发现r测=RV·rRV+r,E测=E·RVRV+r,从形式上看:1r测=1RV+1r,实验中实际上测量的是电源与电压表的并联阻值,这里也包含了某种等效的思想,电源等效思想的理论基础大部分源于等效电压源定理.
等效電压源定理又称戴维南定律,它提供了一种用等效电路取代电路中不变部分的方法,内容可简述为:任一线性含源二端网络可以用一个等效的电动势E0和一个等效内阻r0串联来替换,其中E0等于被换网络开路时的路端电压U0,而r0等于被换网络的除源网络的等效电阻.
将电路图2的虚线框内电路网络等效成新的电压源,根据等效电压源定理其电动势和内阻分别为:E0=ERVRV+r,r0=RV·rRV+r,与用闭合电路欧姆定律推导的形式一致,但处理方式更加简洁直观.
在测小灯泡的伏安特性曲线的实验中,为了达到线性调节的目的,滑动变阻器通常选择小一些的,对于为什么选小的调节方便,很多学生回答不出来,现在用等效电压源定理分析如下:
将图3虚线框内电路网络等效成电流源,如图4其电动势和内阻分别为:E0=ER+r·R1,r0=R1(R2+r)R+r(R1、R2分别为滑动变阻器的左、右部分电阻),等效电源输出电压为:U=E0-I·r0,E0随R1的调节是线性变化的.滑动变阻器阻值较小时,由r0=R1(R2+r)R+r可知等效电源的内阻相对较小,内阻分压I·r0的影响就很小,输出电压的变化也是近似线性的.
对于多电源的问题,利用等效电压源定理简化电路会使解题变得更加方便.如图5所示,两电源电动势和内阻分别为E1E2r1r2,现将电路简化为一个等效电源.
采用闭合电路的欧姆定律分析,设电源E1,r1支路的电流为I1,电源E2,r2支路的电流为I-I1,则有:E1=I1r1+IR
采用闭合电路欧姆定律的分析过程繁琐,计算量大,现采用等效电压源定理分析,等效电源的电动势和内阻分别为:
解法简单明了,若换用n个电动势、内阻分别为E1E2…En,r1r2…rn的电源并联,等效为一个电源时,只需利用数学归纳法得的:
等效电压源原理在实际中还有很多的应用,在电路设计时,对于某一复杂电路需要分析接入不同电阻时的电流,我们不必对接入不同电阻的各种情况做复杂的计算,也不需要对接入不同电阻的情况做重新测量,只需利用等效电压源定理,对开路端电压和除源电路的电阻进行一次测量,便可获得不同电阻情况下输出电压的具体结果.
参考文献:
[1]赵凯华.电磁学\[M\].北京:高等教育出版社,2003(4):321-323.
[责任编辑:李 璟]

