基于时间序列深度学习的超窄间隙焊接质量预测方法

张爱华 魏浩 马晶 白忠领

摘要：焊接过程中，电信号与焊接质量密切相关。超窄间隙焊接是一种高效低热输入的新焊接方法，但其电弧控制与熔滴过渡过程复杂，传统的信号特征提取与分析方法往往不能完整表达和充分利用时间序列信息。结合超窄间隙焊接过程特点，运用完整电信号时间序列构建卷积神经网络，在深入挖掘同属性信号时序信息的同时，充分考虑同步采集的焊接电流和电弧电压信号之间的时间关联信息，对焊接质量进行预测。试验结果表明，基于完整时序信号的深度网络模型能够准确地预测焊接质量，准确率达到95%，在使用RTX2080GPU作为运算加速器的情况下，模型预测所需时间仅为0.178 ms，为实时预测超窄间隙焊接质量奠定了基础。

关键词：超窄间隙;时序数据;卷积网络;质量预测

中图分类号：TG47 文献标志码：A 文章编号：1001-2303（2020）08-0043-05

DOI：10.7512/j.issn.1001-2303.2020.08.09

0 前言

焊接技术在桥梁建设、船舶制造、钢轨维修等工业领域发挥着巨大作用[1-2]。高效低热输入焊接方法是当前的研究热点。可用焊剂片约束电弧的超窄间隙焊接方法，针对4～5 mm的I型坡口，来进行单道多层焊接。由于坡口窄，其所需的焊丝填充量和能耗远小于常规焊接方法，且焊接接头力学性能良好，残余应力和残余变形较小，满足节能、高效及高质量的焊接要求[3]。

超窄间隙焊接的焊缝窄且深，无法观察到熔池，且坡口宽度在焊接过程中会受到热量影响发生变化，而电弧形态对坡口宽度的变化非常敏感，这进一步加大了焊接质量的预测难度，给其现场应用带来了一些限制。目前，基于过程数据的焊接质量预测方法都是根据过程机理进行特征提取，计算出如电弧电压及电流均值、峰值或者波形变化时刻等特征，无法利用完整焊接过程中的时间序列信息，且时效性较差，无法对焊接质量进行快速评估。

寻找包含完整熔滴过渡信息的时序信号与焊接质量之间的映射关系的问题，可称之为时间序列特征引导的预测问题[4]。传统机器学习方法由于其结构性无法很好地提取出时序信号中的信息并将多种同步采集的信号进行时序对应，对时间序列数据的信息挖掘，存在很大的局限性。深度神经网络中的卷积神经网络可以挖掘数据中时间同步的不同种特征之间的潜在关系，同时能在模型构建完成后，快速得到模型输出结果，已经在图像识别、语音识别及无人机领域取得了突破性的进展[5-7]。文中采用深度卷积网络，结合焊接过程中同步采集的电弧电压及焊接电流数据，构建焊接质量预测模型，对超窄间隙焊接接头质量进行预测。

1 焊接试验及数据采集

焊接试验装置由四自由度的机械臂行走机构、伺服电机控制器（SMC6490）、伺服驱动器、弧焊电源（NB-500T）、送丝机、专用焊枪及上位机构成。

上位机中安装有调试软件MOTION6490，使用G代码编写控制程序，通过RJ45网口传送给伺服电机控制器SMC6490。伺服电机驱动机械臂行走机构可带动专用焊枪实现前后、左右、上下、旋转4个自由度方向的运动。在焊接过程中，弧焊电源负责供给电弧能量，依据坡口宽度按照设定的电参数、送丝速度、焊接速度等工艺参数进行焊接，获得单道多层焊接接头。

信号检测与数据采集系统由数据采集卡（NI-6251）、霍尔电流传感器（LHB-600A）、电压变送器（KDV-100V）以及LabVIEW编程软件构成，其中电压变送器两端分别与焊枪和焊接工件连接，电缆穿过霍尔电流传感器后一端与焊接工件相连，另一端接弧焊电源负极。采样频率设置为1 000 Hz，同步采集焊接过程中的电弧电压与焊接电流信号。

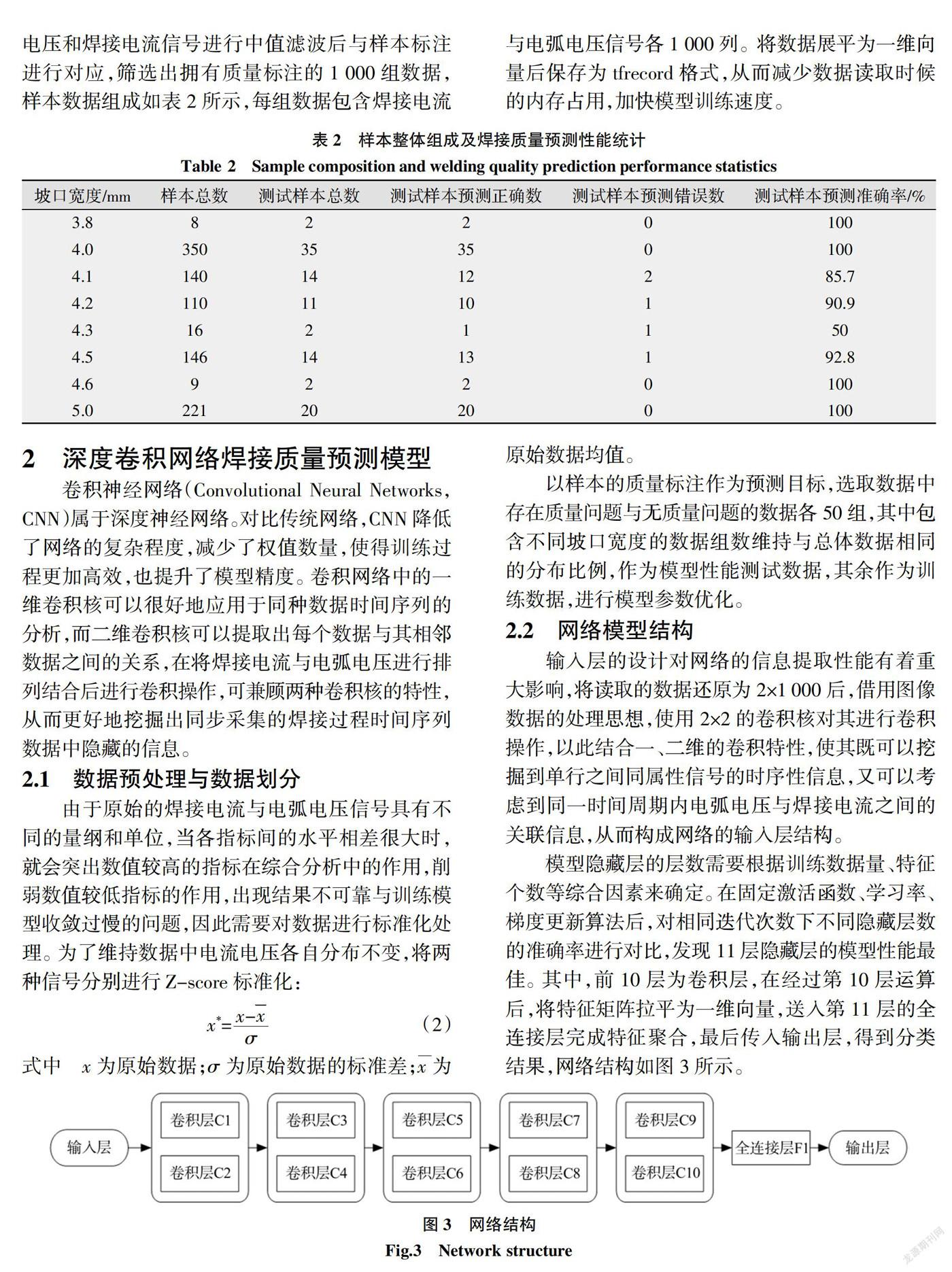
将两块截面积为30 mm×30 mm×200 mm的Q235钢材通过点焊固定在3 mm厚钢板上，制成如图1所示的焊件，使用焊剂片约束电弧的超窄间隙焊接方法进行焊接试验。试验工艺参数见表1，将坡口宽度作为变量，从3.8 mm开始递增，并在同一坡口宽度下改变预置电压、电流来进行焊接。

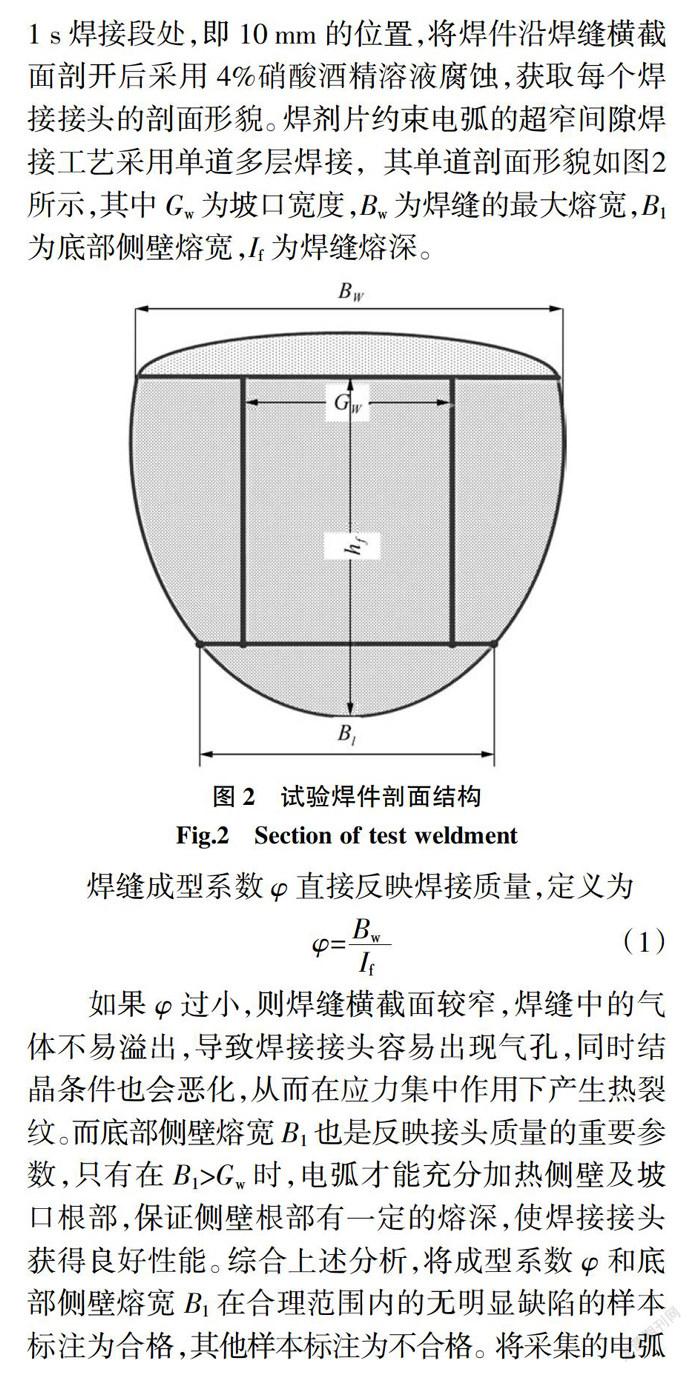
试验所采用的焊接速度为9～10 mm/s，在间隔1 s焊接段处，即10 mm的位置，将焊件沿焊缝横截面剖开后采用4%硝酸酒精溶液腐蚀，获取每个焊接接头的剖面形貌。焊剂片约束电弧的超窄间隙焊接工艺采用单道多层焊接，其单道剖面形貌如图2所示，其中Gw为坡口宽度，Bw为焊缝的最大熔宽，B1为底部侧壁熔宽，If为焊缝熔深。

焊缝成型系数φ直接反映焊接质量，定义为

φ=（1）

如果φ过小，则焊缝横截面较窄，焊缝中的气体不易溢出，导致焊接接头容易出现气孔，同时结晶条件也会恶化，从而在应力集中作用下产生热裂纹。而底部侧壁熔宽B1也是反映接头质量的重要参数，只有在B1>Gw时，电弧才能充分加热侧壁及坡口根部，保证侧壁根部有一定的熔深，使焊接接头获得良好性能。综合上述分析，将成型系数φ和底部侧壁熔宽B1在合理范围内的无明显缺陷的样本标注为合格，其他样本标注为不合格。将采集的电弧电压和焊接电流信号进行中值滤波后与样本标注进行对应，筛选出拥有质量标注的1 000组数据，样本数据组成如表2所示，每组数据包含焊接电流与电弧电压信号各1 000列。将数据展平为一维向量后保存为tfrecord格式，从而减少数据读取时候的内存占用，加快模型训练速度。

2 深度卷积网络焊接质量预测模型

卷積神经网络（Convolutional Neural Networks，CNN）属于深度神经网络。对比传统网络，CNN降低了网络的复杂程度，减少了权值数量，使得训练过程更加高效，也提升了模型精度。卷积网络中的一维卷积核可以很好地应用于同种数据时间序列的分析，而二维卷积核可以提取出每个数据与其相邻数据之间的关系，在将焊接电流与电弧电压进行排列结合后进行卷积操作，可兼顾两种卷积核的特性，从而更好地挖掘出同步采集的焊接过程时间序列数据中隐藏的信息。

2.1 数据预处理与数据划分

由于原始的焊接电流与电弧电压信号具有不同的量纲和单位，当各指标间的水平相差很大时，就会突出数值较高的指标在综合分析中的作用，削弱数值较低指标的作用，出现结果不可靠与训练模型收敛过慢的问题，因此需要对数据进行标准化处理。为了维持数据中电流电压各自分布不变，将两种信号分别进行Z-score标准化：

x*=（2）

式中 x为原始数据;σ为原始数据的标准差;x为原始数据均值。

以样本的质量标注作为预测目标，选取数据中存在质量问题与无质量问题的数据各50组，其中包含不同坡口宽度的数据组数维持与总体数据相同的分布比例，作为模型性能测试数据，其余作为训练数据，进行模型参数优化。

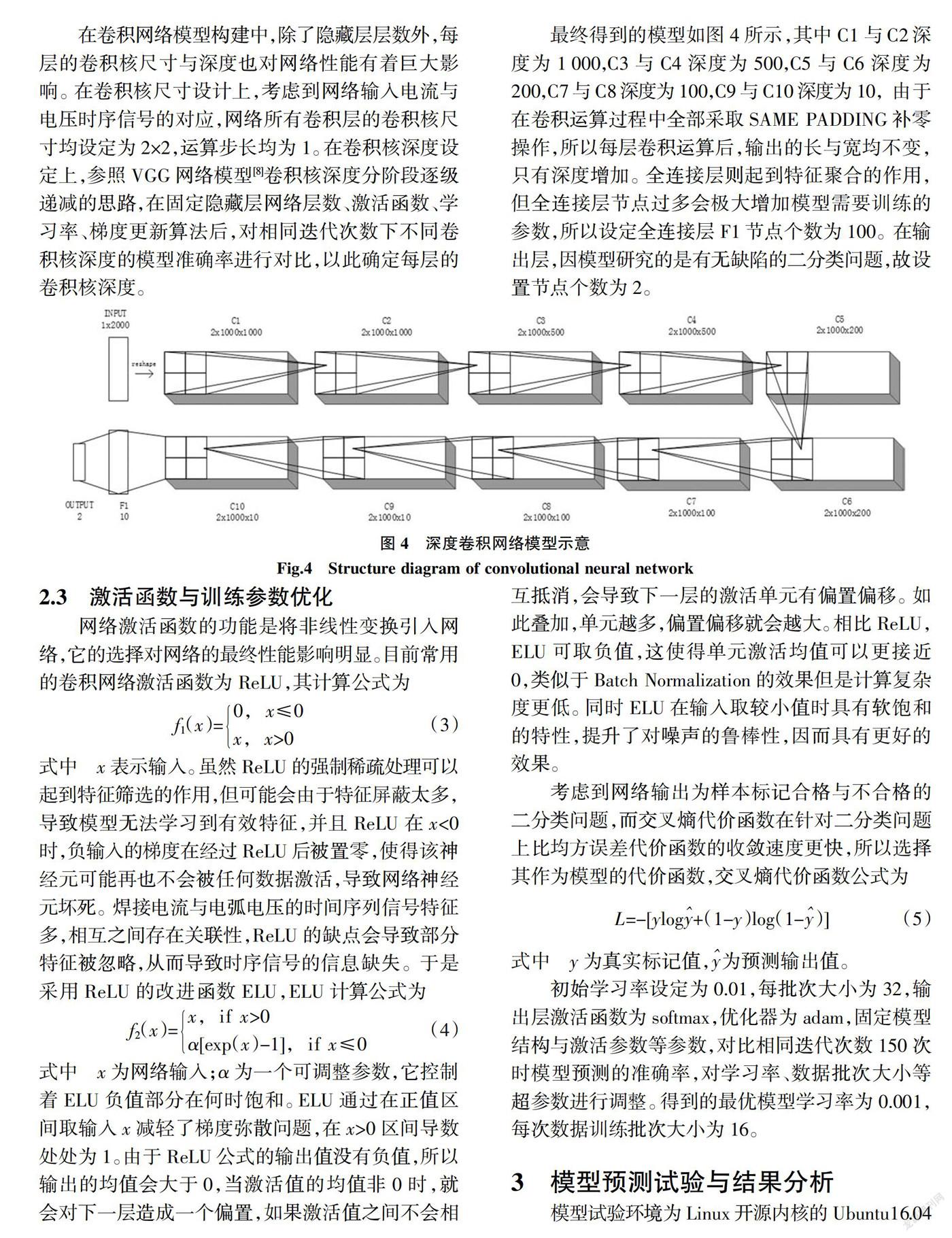
2.2 网络模型结构

输入层的设计对网络的信息提取性能有着重大影响，将读取的数据还原为2×1 000后，借用图像数据的处理思想，使用2×2的卷积核对其进行卷积操作，以此结合一、二维的卷积特性，使其既可以挖掘到单行之间同属性信号的时序性信息，又可以考虑到同一时间周期内电弧电压与焊接电流之间的关联信息，从而构成网络的输入层结构。

模型隐藏层的层数需要根据训练数据量、特征个数等综合因素来确定。在固定激活函数、学习率、梯度更新算法后，对相同迭代次数下不同隐藏层数的准确率进行对比，发现11层隐藏层的模型性能最佳。其中，前10层为卷积层，在经过第10层运算后，将特征矩阵拉平为一维向量，送入第11层的全连接层完成特征聚合，最后传入输出层，得到分类结果，网络结构如图3所示。

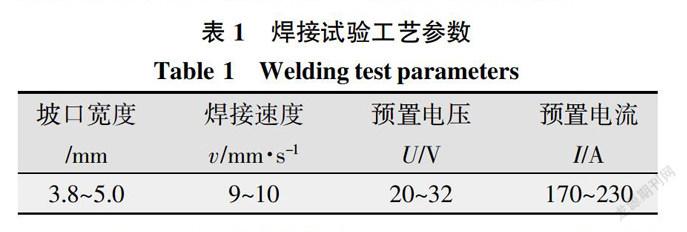
在卷积网络模型构建中，除了隐藏层层数外，每层的卷积核尺寸与深度也对网络性能有着巨大影响。在卷积核尺寸设计上，考虑到网络输入电流与电压时序信号的对应，网络所有卷积层的卷积核尺寸均设定为2×2，运算步长均为1。在卷积核深度设定上，参照VGG网络模型[8]卷积核深度分阶段逐级递减的思路，在固定隐藏层网络层数、激活函数、学习率、梯度更新算法后，对相同迭代次数下不同卷积核深度的模型准确率进行对比，以此确定每层的卷积核深度。

最终得到的模型如图4所示，其中C1与C2深度为1 000，C3与C4深度为500，C5与C6深度为200，C7与C8深度为100，C9与C10深度为10，由于在卷积运算过程中全部采取SAME PADDING补零操作，所以每层卷积运算后，输出的长与宽均不变，只有深度增加。全连接层则起到特征聚合的作用，但全连接层节点过多会极大增加模型需要训练的参数，所以设定全连接层F1节点个数为100。在输出层，因模型研究的是有无缺陷的二分类问题，故设置节点个数为2。

2.3 激活函数与训练参数优化

网络激活函数的功能是将非线性变换引入网络，它的选择对网络的最终性能影响明显。目前常用的卷积网络激活函数为ReLU，其计算公式为

f1（x）=0，  x≤0

x，  x>0（3）

式中 x表示输入。虽然ReLU的强制稀疏处理可以起到特征筛选的作用，但可能会由于特征屏蔽太多，导致模型无法学习到有效特征，并且ReLU在x<0时，负输入的梯度在经过ReLU后被置零，使得该神经元可能再也不会被任何数据激活，导致网络神经元坏死。焊接电流与电弧电压的时间序列信号特征多，相互之间存在关联性，ReLU的缺点会导致部分特征被忽略，从而导致时序信号的信息缺失。于是采用ReLU的改进函数ELU，ELU计算公式为

f2（x）=x，  if x>0

α[exp（x）-1]，  if x≤0（4）

式中 x为网络输入;α为一个可调整参数，它控制着ELU负值部分在何时饱和。ELU通过在正值区间取输入x减轻了梯度弥散问题，在x>0区间导数处处为1。由于ReLU公式的输出值没有负值，所以输出的均值会大于0，当激活值的均值非0时，就会对下一层造成一个偏置，如果激活值之间不会相互抵消，会导致下一层的激活单元有偏置偏移。如此叠加，单元越多，偏置偏移就会越大。相比ReLU，ELU可取负值，这使得单元激活均值可以更接近0，类似于Batch Normalization的效果但是计算复杂度更低。同时ELU在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性，因而具有更好的效果。

考虑到网络输出为样本标记合格与不合格的二分类问题，而交叉熵代价函数在针对二分类问题上比均方误差代价函数的收敛速度更快，所以选择其作为模型的代价函数，交叉熵代价函数公式为

L=-[ylog+（1-y）log（1-）]（5）

式中 y为真实标记值，为预测输出值。

初始学习率设定为0.01，每批次大小为32，输出层激活函数为softmax，优化器为adam，固定模型结构与激活参数等参数，对比相同迭代次数150次时模型预测的准确率，对学习率、数据批次大小等超参数进行调整。得到的最优模型学习率为0.001，每次数据训练批次大小为16。

3 模型预测试验与结果分析

模型试验环境为Linux开源内核的Ubuntu16.04应用系统，使用python语言编程的Keras深度学习框架对模型进行实现，用一块8 GB显存的英伟达（NVIDIA）RTX2080顯卡进行加速运算。

根据前述的模型结构，在维持训练集与测试集正负样本分布不变的情况下，多次随机划分训练集与测试集，多次试验后，该模型测试集最低预测准确率为95%，最高为99%，模型每次迭代耗时27 s，正向运行时间为0.178 ms。最低准确率的评估结果如图5所示，其中质量合格的50组样本中有47组预测与真实标记一致，3组预测错误，存在质量问题的50组样本中有48组预测与真实标记一致，2组样本预测错误，其预测性能统计见表2。

试验表明，使用焊接过程中电弧电压与焊接电流的时序信号作为输入构建深度网络模型对焊接质量进行预测，准确率为95%以上，可以很好地反映数据与质量之间的映射关系，其中有5组测试样本未被正确识别，可能的原因如下：采集的时序数据中存在一定噪声，破坏了时序性数据之间的相关规律，导致其与标记映射关系存在误差;模型网络深度可能过深，导致训练集的数量不足以使模型完全收敛，存在过拟合现象;数据采集的采样频率相对较低，无法更进一步描绘出焊接过程细微信号的变化，从而导致与样本标记质量存在偏差。此外，通过不同坡口宽度的样本预测性能对比，发现模型对样本组数较多的坡口宽度如5.0 mm和4.0 mm，焊接质量预测能力更为突出，准确率达100%;对样本组数相对较少的坡口宽度，在预测性能上存在一定程度的波动，可见坡口宽度和样本组数也对模型的预测性能存在一定影响。

4 结论

针对超窄间隙焊接工艺过程中时序数据隐藏信息难以提取的特点，使用深度卷积网络对时序数据进行信息提取，构建了焊接质量预测模型。对模型进行训练与测试后，准确率达到95%以上，表明充分利用电弧电压和焊接电流信息可以较好地预测焊接质量，模型在使用RTX2080GPU作为运算加速器的条件下，预测所需时间仅为0.178 ms，满足未来进行焊接质量在线预测的速度要求，为焊接质量的实时在线预测奠定了基础。但模型在预测性能上还有待提升，可制作更多不同坡口宽度的样本进行试验采集焊接数据，并将坡口宽度、送丝速度等因素也作为构建模型的考虑范畴以进一步提升模型的泛化能力和预测准确性。

参考文献：

[1] MORADI M，GHOREISHI M，FROSTEVARG J，et al. An investigation on stability of laser hybrid arc welding[J]. Optics Lasers in Engineering，2013，51（4）：481-487.

[2] LEE S J，KIM Y H，KIM J K，et al. A roll-to-roll welding process for planarized silver nanowire electrodes[J]. Nan- oscale，2014，6（20）：11828-11834.

[3] 郑韶先，朱亮，黄斌维，等. 焊剂带约束电弧用于超窄间隙的焊接[J]. 机械工程学报，2009，45（2）：219-223.

[4] 郭躬德，王晖，David Bell. 时间序列数据分析与预处理 [J]. 小型微型计算机系统，2003（12）：2228-2232.

[5] TANG J，DENG C，HUANG G，et al. Compressed-Domain Ship Detection on Spaceborne Optical Image Using Deep Neural Network and Extreme Learning Machine[J]. IEEE Transactions on Geoscience Remote Sensing，2015，53（3）： 1174-1185.

[6] Otsu N. A Threshold Selection Method from Gray-Leve Histograms[J]. IEEE Transactions on Systems Man Cybernetics，2007，9（1）：62-66.

[7] 王科俊，趙彦东，邢向磊. 深度学习在无人驾驶汽车领域应用的研究进展[J]. 智能系统学报，2018，69（1）：59-73.

[8] SIMONYAN K，VEDALDI A，ZISSERMAN A. Learning Local Feature Descriptors Using Convex Optimisation[J]. IEEE Transactions on Pattern Analysis Machine Intelligence，2014，36（8）：1573-1585.

收稿日期：2020-04-21

基金项目：国家自然科学基金（61866021）;甘肃省科技计划项目（18YF1WA068）;兰州市人才创新创业项目（2016-RC-72）

作者简介：张爱华（1964— ），女，教授，博导，主要从事检测技术与智能信息处理的研究。E-mail：435120071@qq.com。