高压油管压力控制的数学模型

钱兴新 金志远 张梦媛

摘要：燃油发动机对于我们日常生活中的机械工作有着重要作用。燃油进入和喷出高压油管是许多燃油发动机工作的基础，燃油进入和喷出油管的间歇性工作过程会导致高压油管内压力的变化，使得所喷出的燃油量出现偏差，从而影响发动机的工作效率。本文研究发动机中进入和进出高压油管的燃油量，通过控制高压油管的压力保持稳定来提高发动机的工作效率。为维持高压油管压强稳定在100MPa或经历调整时长上升到150MPa后保持稳定。我们根据压强的变化量建立微分方程，将压强随时间的变化离散到每个进油周期，利用隐式欧拉法求解微分方程。

关键词：微分方程;质量守恒;隐式欧拉算法;优化模型

0  引言

燃油进入和喷出高压油管是许多燃油发动机工作的基础，燃油经过高压油泵从A处进入高压油管，再由喷口B喷出。燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化，使得所喷出的燃油量出现偏差，从而影响发动机的工作效率。为维持油管内压强稳定，我们着重研究以下两个问题：确定单向阀开启的时长，以保证油管内的压强尽可能稳定在100MPa;调整单向阀开启的时长，使油管内的压强分别经过2s，5s和10s的调整过程稳定在150MPa。

1  模型假设

①不考虑各部件弹性变形。

②不考虑温度变化对压力，体积的影响。

③不考虑压力变化时间，同一腔室内燃油压力及密度处处相同。

2  符号说明

①t0单向阀开启时长;

②ρ燃油密度;

③P燃油压力;

④Q进出油流量;

⑤m燃油质量;

⑥E弹性模量。

3  问题分析

求给出压强维持在100MPa和压强从100MPa上升到150MPa的情况下的单向阀开启时长，根据压强变化量与密度变化量成正比，建立微分模型，将压强随时间的变化离散到各个进油周期，用隐式欧拉算法进行迭代求解微分方程数值解，表示出压强随时间的变化，最后使其稳定在一定值求解出单向阀每次开启的时间。对于压强调整过程也是如此求解，调整过程后的保持稳定的过程则与前述的稳定过程求解一样。

4  模型建立与求解

4.1 模型分析

问题一需要求解单向阀开启的时长，根据压强变化量与密度变化量成正比，表示出进出油与压强的关系，建立微分方程模型，求解压强随时间的变化关系，保持压强不变的情况下，取出油周期100ms，以100ms末的压强值与100MPa的差值最小为目标，对t0遍历搜索，求解维持稳定的单向阀开启时长t0（ms）。对于压强从100MPa增加到150MPa的调整过程，在t1（s）的调整时长内，将压强随时间的连续变化离散化为每一个进油的周期t0+10内，同样求解微分方程， 以t1末的压强值与150MPa的差值最小为目标，求解调整过程单向阀开启t0。而t1后的稳定过程的单向阀开启时长同第一子问相同。

4.2 公式推导

4.2.1 燃油压力与密度的关系式

根据注1，燃油压力变化量与密度变化量成正比，且已知比例系数，初始条件得到：

根据数据弹性模量与压力的关系，对与进行二次拟合得到拟合关系式：

将（2）式代入（1）式求解此微分方程得到：

4.2.2 流量与管内压力，时间的关系

进油处压力稳定在160MPa，则进油处密度也为恒定值，代入（3）式得到：

由注2，进出油流量：

此时小孔面积A0=0.49π。

则在单向阀开关的一个周期内t0+10：

根据喷油速率，以及出油频率，可以得到1个周期（100ms）：

4.2.3 关于压强的微分方程[1]

根据注1，有油管连续性方程：

容器体积为V0，可以得到[2]：

其中

将式（2）（7）（6）代入式（8），得到：

其中Q入由式（6）给出，Q出由式（7）给出。

4.3 压强维持100MPa时的模型建立与求解

4.3.1 模型建立

①目标函数的确立。

根据优化目标需要使压强稳定在100MPa，我们取出油周期100ms，将周期末的压强值作为优化目标，得到：

P（100）表示100ms对应的压强值。

②约束条件的表示。

对于上述过程，其约束条件为压强值关于时间的微分方程求解。

因为一次出油的周期明显长于一次进油周期，故考虑一次出油周期，即100ms末的压强与100MPa的差值最小，对应求出单向阀开启时长即可。

在时间起点的第一个t0+10内，不考虑压强变化时对t0做估计其值应在0.2到2.2s之间，即恒定出油的时候。根据进出油的周期性，在一个出油周期内得到：

而在t0+10到100ms内，

其中：T进=t0+10，表示进油周期。代入（9）式微分方程求解。

综合以上分析，建立优化模型：

4.3.2 模型求解

欧拉算法[4]

对于问题一中的微分方程，由于微分方程比较复杂，难以求解其解析解，故利用matlab用隐式欧拉法求解其数值解。对于上述微分方程，微分方程模型为：

计算P（t）在[a，b]区间上N个等间距点的近似值。

隱式欧拉算法如下：

Step1 计算N个等间距点构成的区间长度

Step2输出（t，P）

Step3对i=1，2，…N重复step4和Step5

Step4 计算下一时刻压强值

Step5 输出每个（ti，Pi）

求解结果：

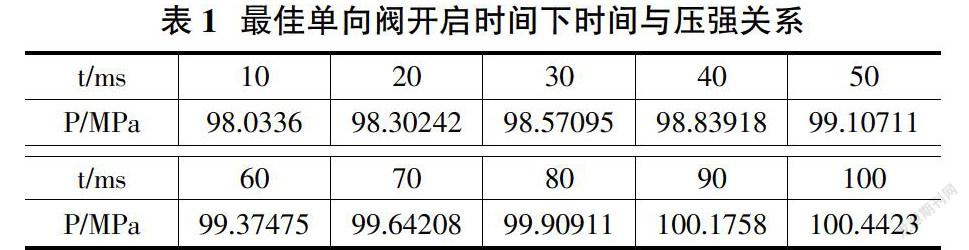
根据隐式欧拉算法，即向后差分的思想对t0遍历后，求解100ms末的压强得到，t0取0.31（ms）时压强最接近100MPa。以0.01s为步长，求解得到部分结果见表1。

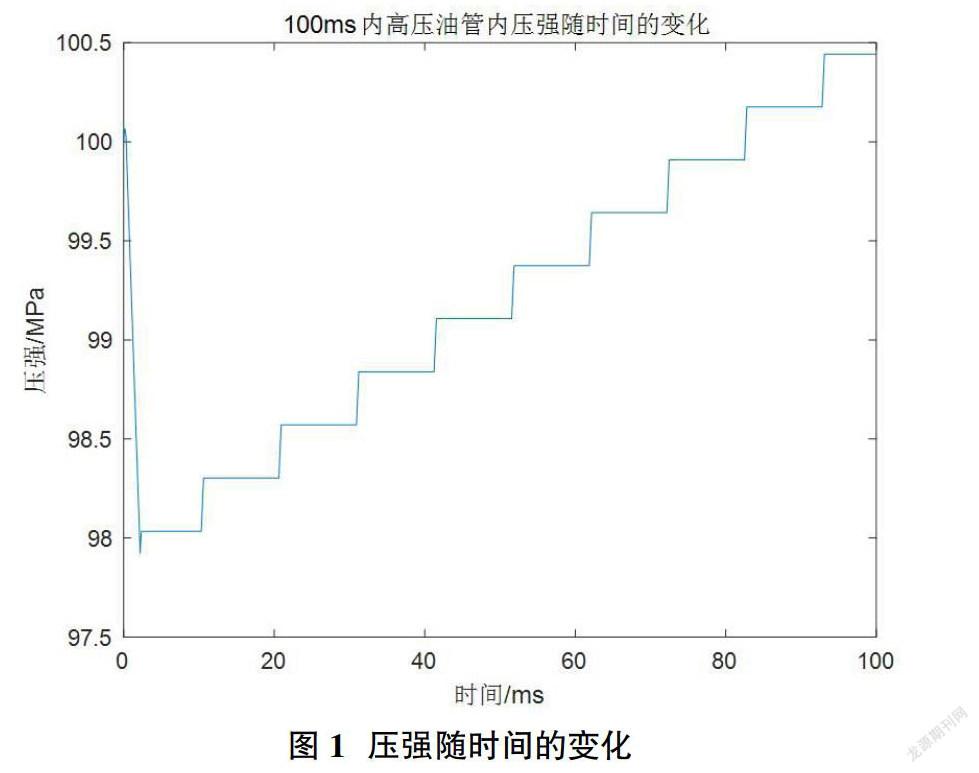
利用求解到的每个t与P的关系作出压强随时间变化的图像如图1。

从表1和图1上可以看出：

①压强随时间是一个波动的过程，在100ms时压强值为100.4423，趋近于100MPa。

②在刚开始的一段时间内，压强迅速降低是因为在2.4ms内出油迅速，而进油很少使管内质量下降，导致压强下降。

③2.4ms以后压强有波动的回升是因为在接下来的时间内，出油量为0，而进油量还在经历周期性的过程，即进油量的周期性增加导致压强回升。

④压强回升呈现类似于阶梯状反映了在t0=0.31ms的单向阀开启时间内，燃油迅速流入，没有流出，故压强增大得较快，而在余下的10ms内没有进出油故压强保持不变。且“阶梯”的分布也反映了单向阀开启时间相较关闭时间较短的特点，即反映在：“阶梯”图形的上升段很陡，时间短，持平段时间长，压强不变。

4.4 压强经历调整过程的模型建立与求解

4.4.1 模型建立

同样我们的优化目标在于调整过程结束后的压强值稳定在150MPa。

优化模型：

4.4.2 模型求解

同理对于（9）式建立的微分模型，用压力稳定在100MPa时的方法，在100ms内讨论每个进油周期，但对于由多个100ms组成的过程，由于进出油周期的不一致，100ms结束后不一定能回到初始状态，但由于单向阀开启的时长相较于关闭的时长比较短，故我们总是假设经过100ms的循环后能回到与0时刻相同的状态。在此条件下求解模型。

同样用隐式欧拉法求解微分方程，得到不同调整时长下单向阀最佳开启时长。

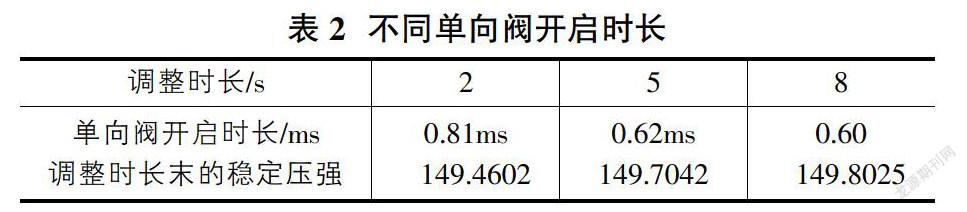
结果如表2。

从表格可以看出：

①随着调整时长的增加，单向阀开启时长减少，反映了调整时间内油管总体质量的增加应该是一个较为稳定的量，从压强增加值保持稳定量来看，因为压强变化量与密度变化量成正比，而体积不变，故质量变化量也应该是较为稳定。

②调整时长越长，稳定压强与150MPa越接近，说明调整过程是一个渐变的波动过程，逐渐趋于稳态。

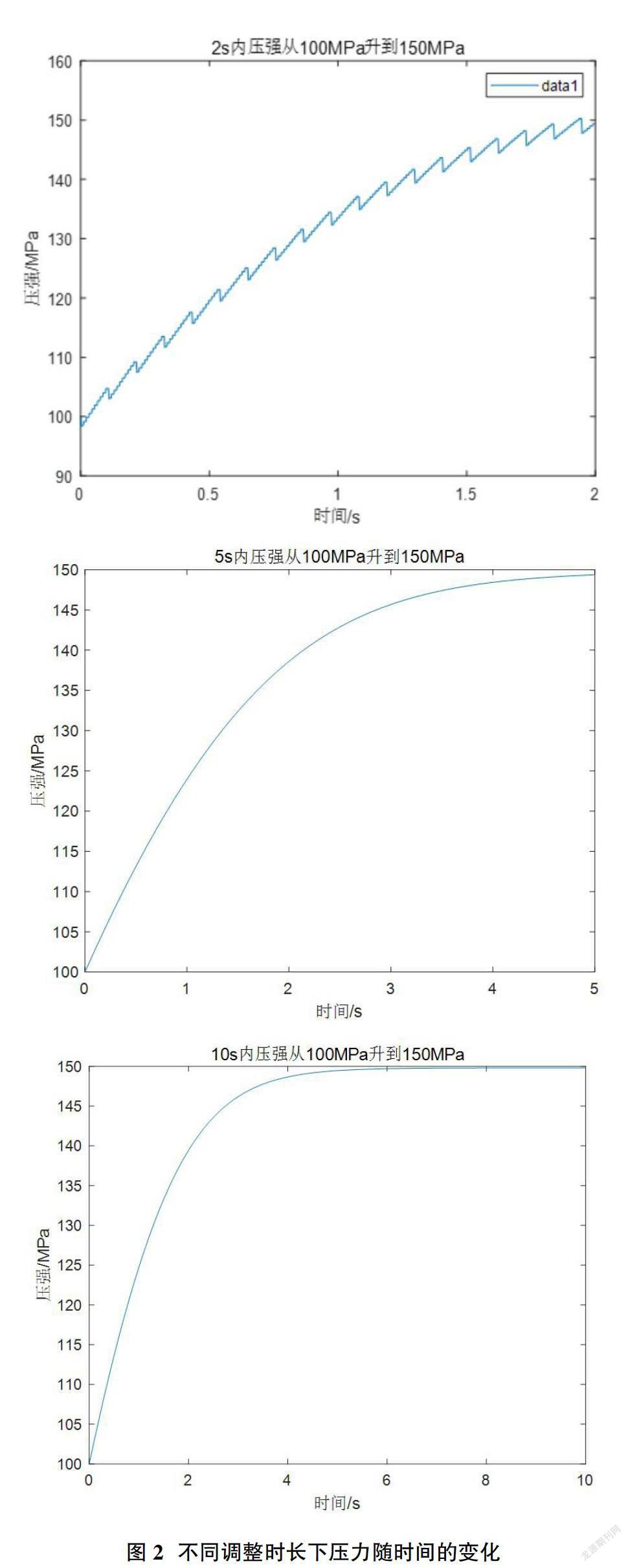
同样，作出2s，5s调整过程中的压力随时间变化的曲线，得到图2。

观察图2并进行对比，可以得出：

①2秒时压强变化呈现波动，渐趋稳定，反映了2s内每个100ms的进出油的特性。当调整时长变长时曲线更加平滑，反映了更长的调整时长内，进出油周期性变化被削弱。

②调整时长增加时，达到稳定的时间值也逐渐增长，说明压强的调整过程是一个对时间敏感的量，对应于我们求解微分方程时用隐式欧拉法的时间上的迭代也有很好的说明效果。

5  结论

根据压强稳定的条件得出维持压强在100MPa保持稳定的单向阀每次开启时长为0.31ms。同理求解出经历2s，5s，10s调整时长过程中的单向阀每次开启时长分别为：0.81ms，0.62ms，0.60ms。经过调整时长之后保持150MPa稳定压强的单向阀每次开启时长如前面一致为0.31ms。

参考文献：

[1]吕晓辰.高压共轨系统高压管路压力波动特性仿真研究及结构优化[D].北京交通大学.

[2]吴健.柴油机共轨式电控喷射系统喷射过程的模拟计算和研究[D].湖南大学，2016.

[3]姜启源，谢金星，叶俊.数学模型[M].四版.北京：高等教育出版社，2011.

[4]司守奎，孫兆亮.数学建模算法与应用[M].二版.北京：国防工业出版社，2015.