2020年中考数学模拟卷(二)



(考试时间:120分钟 试卷满分:120分)
一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号写在题后的括号内,每小题2分,共20分)
1. [-25]的相反数是( ).
A. [25] B. [52] C. [-52] D. [-25]
2. [2020]的整数部分是( ).
A. 42 B. 43 C. 44 D. 45
3. 2020年上半年,一种新型冠状病毒在世界范围内暴发,我国在控制住国内疫情的同时,展现了大国担当,第一时间向世界卫生组织捐款2000万美元,约合人民币1.38亿元,将数字1.38亿用科学记数法表示为( ).
A. 1.38 × 108 B. 1.38 × 109 C. 13.8 × 107 D. 13.8 × 108
4. 下列运算正确的是( ).
A. [a6÷a2=a3] B. [5a2-4a2=a2]
C. [(3a2)3=9a6] D. [12a·4a2=2a2]
5. 二次函数y = -3x2 - 6x + 5的图象的顶点坐标是( ).
A. (1,-4) B. (1,8) C. (-1,2) D. (-1,8)
6. 已知α为锐角,且tan(α - 20°) = [33],则α等于( ).
A. [50°] B. [60°] C. [70°] D. [80°]
7. 如图1,四边形ABCD是⊙O的内接四边形,∠BAD = 60°,且CD = BC,若AC = 4,则四边形ABCD的面积为( ).
A. 4 B. 16
C. [43] D. [163]
8. 反比例函数[y=mx]与正比例函数[y=nx]的图象相交于A(5,a)和B(b,7)两点,那么a + b等于( ).
A. 35 B. -12 C. -32 D. 12
9. 已知[abc≠0],且[b=a+c],那么关于x的一元二次方程[ax2+bx+c=0]必有一个根为( ).
A. 1 B. 2 C. -1 D. -2
10. 如图2,△ABC中,AC = 3,BC = 4,AB = 5,点D,E,F分别在AB,AC,BC上,且∠EDF = 90°,若CD为△ABC的高线,则EF的最小值为( ).
A. [125] B. [52]
C. 2 D. [32]
二、填空题(每小题3分,共18分)
11. [-12]的倒数是 .
12. 边长为2的正六边形的面积为 .
13. 如图3,矩形ABCD中,AD = 6,AB = 8,点M,N,E,F分别在CD,AB,AD,BC上,EF⊥MN,若MN = 7,则EF = .
14. 若a2-2ab = 0(b ≠ 0),则[aa+b=] .
15. 若直线[y=-43x+b]与[y=-43x-2]之间的距离为3,那么b = .
16. 如图4,在平面直角坐标系中,点A的坐标为(-2,3),点B的坐标为(1,4),点C是x轴上的动点,将线段AB沿着AC折叠,点B恰好落在x轴上,则点C的坐标为 .
三、解答题(第17题6分,第18、19题各8分,共22分)
17. 计算:([3] + 2)(2 - [3]) + [13-2] - 4[3]tan 60°.
18. 现有6张外形完全相同的卡片,上面分别写着1,2,3,4,5,6.
(1)把它们放在一个不透明的口袋中,随机摸出两张卡片,那么两张卡片上数字都是奇数的概率为 .
(2)把6张卡片放入甲、乙两个不透明口袋,其中甲口袋中卡片上的数字是1,2,3,从两个口袋中各摸一张,用列表法或画树状图的方法求出两次摸到的卡片上数字都是奇数的概率.
19. 如图5,四边形ABCD是矩形,AB = 3,BC = 4,BD的垂直平分线交AD,BD,BC于E,G,F,连接BE,DF.
(1)求证:四边形BEDF是菱形.
(2)菱形BEDF的面积为 .
20.某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班全体学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如图6所示的扇形统计图和不完整的条形图:
(1)该班共有学生 人.
(2)该班学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”觀点所在扇形区域的圆心角是 度.
(3)直接将条形图补充完整.
(4)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人.
四、(本题16分)
21. 如图7,△ABC中,AB = AC = 5,以AB为直径作⊙O,交AC于点E,交BC于点D,连接BE,DE,已知tan∠BED = [34].
(1)求BD的长.
(2)求DE = ,CE = .
五、(本题10分)
22. 已知直线[y=12x]与双曲线[y=kx](x > 0)在第一象限交于点A,且点A的横坐标为4. 若双曲线[y=kx](x > 0)上一点[C]的纵坐标为8,求△AOC的面积.
六、(本题10分)
23.某商店以每件40元的价格购进一批商品. 当售价为每件60元时,每星期可卖出300件,现需降价处理,经市场调查发现:每降价1元,每星期可多卖出20件. 在确保盈利的前提下,解答下列问题:
(1)如果每件的售价定为55元,这一周商场可以获利多少元?
(2)商场一周获利能否达到6080元?如果可以,求出此时的售价;如果不可以,请说明理由.
(3)当降价多少元时,每星期的利润最大?最大利润是多少?
(4)小王认为,利润最大,营业额也最大. 对吗?举例说明.
七、(本题12分)
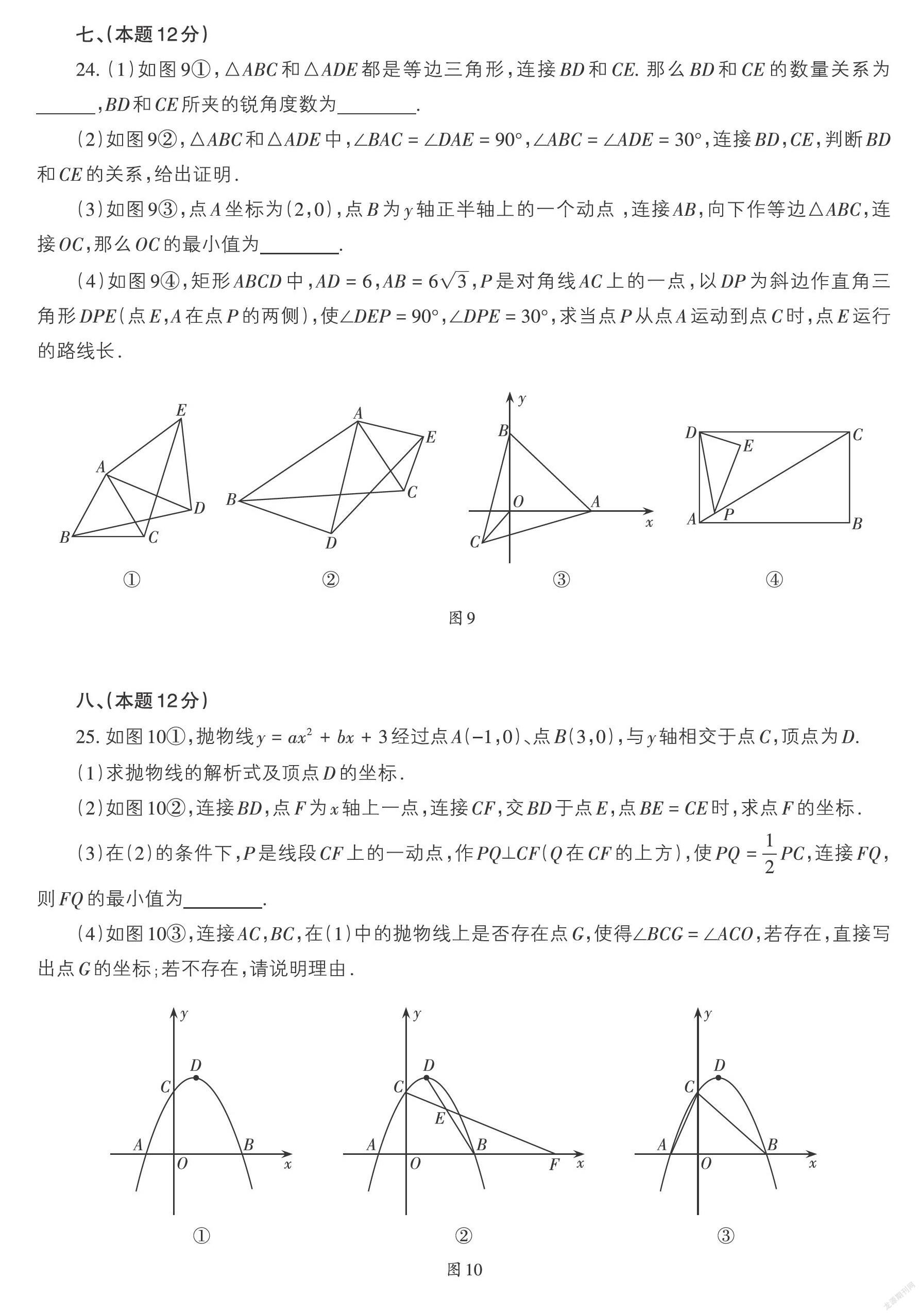
24. (1)如图9①,△ABC和△ADE都是等边三角形,连接BD和CE. 那么BD和CE的数量关系为 ,BD和CE所夹的锐角度数为 .
(2)如图9②,△ABC和△ADE中,∠BAC = ∠DAE = 90°,∠ABC = ∠ADE = 30°,连接BD,CE,判断BD和CE的关系,给出证明.
(3)如图9③,点A坐标为(2,0),点B为y轴正半轴上的一个动点 ,连接AB,向下作等边△ABC,连接OC,那么OC的最小值为 .
(4)如图9④,矩形ABCD中,AD = 6,AB = [63],P是对角线AC上的一点,以DP为斜边作直角三角形DPE(点E,A在点P的两侧),使∠DEP = 90°,∠DPE = 30°,求当点P从点A运动到点C时,点E运行的路线长.
八、(本题12分)
25. 如图10①,抛物线[y=ax2+bx+3]经过点A(-1,0)、点B(3,0),与y轴相交于点C,顶点为D.
(1)求抛物线的解析式及顶点D的坐标.
(2)如图10②,连接BD,点F为x轴上一点,连接CF,交BD于点E,点BE = CE时,求点F的坐标.
(3)在(2)的條件下,P是线段CF上的一动点,作PQ⊥CF(Q在CF的上方),使[PQ=12PC],连接FQ,则FQ的最小值为 .
(4)如图10③,连接AC,BC,在(1)中的抛物线上是否存在点G,使得∠BCG = ∠ACO,若存在,直接写出点G的坐标;若不存在,请说明理由.

