运用思维导图分析 培养高阶思维能力
于发书 曾飞鹏

[摘 要] 为了解决学生对解决几何综合题感到困难的问题,文章通过引导学生绘制思维导图,从而加强大脑的发散思维能力,提供给学生分析问题和解决问题的一种思维范式,以达到培养学生高阶思维能力的目的.
[关键词] 思维导图;高阶思维;思维可视化
常态数学课堂教学在不同程度上还存在“三多三少”现象,即教师讲得多,提炼得少;学生做得多,思考得少;现成资料多,自主设计少. 这种现象导致学生在课堂上听得懂,但在课后遇到新的问题,特别是在解决一些比较棘手的压轴题时还是打不开思路. 这种现象从根本上来讲,是因为教师高密度、低认知水平的课堂提问,和大容量、重复式的习题训练不能提升甚至限制了学生高阶思维的发展. 布鲁姆将教育目标从认知维度分为記忆、理解和运用,分析、评价和创造. 高阶思维是指发生在高层次认知水平上的心智活动,它对应教学目标分类中诸如分析、综合、评价等高层次认知水平的能力,是创新能力、问题解决能力、决策力和批判思维能力的核心. 如何将抽象的、看似难以企及的高阶思维能力培养变得有章可循,变得具体形象?这是摆在教师面前的一大课题. 而思维导图是用图表表现的发散性思维,发散性思维过程也就是大脑思考和产生想法的过程. 通过捕捉和表达发散性思维,思维导图将大脑内部的思维过程进行了外部呈现. 本质上,思维导图是在重复和模仿发散性思维,反过来又放大了大脑的本能,让大脑的思维更加有力.
本文就如何在课堂上利用思维导图辅助教学,从而培养学生的高阶思维能力加以简单论述. 下面以2018年珠海市香洲区统考数学试卷的第24题第(3)问的讲评为例来说明.
试题特点
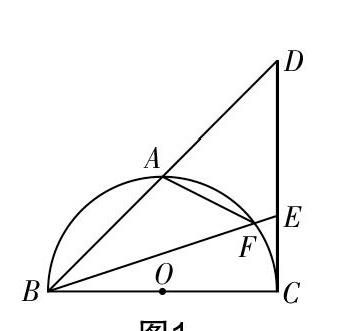
原题呈现:如图1,BC为⊙O的直径,点A是弧BC的中点,连接BA并延长至点D,使得AD =AB,连接CD,点E为CD上一点,连接BE交弧BC于点F,连接AF.
(1)求证:CD为⊙O的切线;
(2)求证:∠DAF=∠BEC;
(3)若 DE=2CE=4,求AF的长.
本题第(3)问以圆为背景,涵盖了等腰直角三角形、全等三角形、相似三角形等知识,综合性强,灵活性大. 而且如果就题讲题,学生的收获甚微,但如果能运用思维导图辅助教学,不仅可以条理清晰地讲清本题的思路,还能将让解题思路可视化,通过对一道题的研究,从而获得诸如求线段长这一类问题的解题方法.
问题解决
在上课前,让学生首先就求线段长的方法绘制一张思维导图,一般的同学都可以绘制出如图2所示的思维导图,但每一种方法的处理策略是什么?很多学生对此是茫然的. 正因为如此,很多学生在解决这类问题的时候找不到思路和突破口. 下面从三个方面来研究.
1. 勾股定理法
要用勾股定理法求线段的长,则必须将所求线段放置于直角三角形中,若所求线段不在直角三角形中,则应作垂线,构造直角三角形. 一般情况下,为了将所求线段完整地求出来,往往会过所求线段的端点作垂线. 按照这种思路,本题有如图3的几种思考.
由(1)(2)知,AC⊥AB,AC=AB,CF⊥BE,从而 BE=2■,CF=■,BF=■,AC=3■. 要求AF的长,可构造含AF的直角三角形. 按照图3的构思,我们加以尝试.
法1:如图4,过点A作AG⊥AE交BE于点G,显然,出现手拉手全等模型,即△ACF≌△ABG(ASA)所以BG=CF,AG=AF,△AGF为等腰直角三角形. GF=BF-BG=■,所以AF=■.
法2:如图5,过点A作AH⊥BE于H. 因为∠AFH=∠ACB=45°, 所以△AHF是等腰直角三角形,设HF=x,则HA=x,BH=BF-HF=■-x.又AB=3■,在Rt△AHB中,由勾股定理得,x=■,所以AF=■.
法3:如图6,作AN⊥CF于点N. 易得∠AFN=45°,设AN=x,则FN=x,在Rt△CAN中,由勾股定理得,x=■,所以AF=■.
法4:如图7,作FQ⊥AC,设FQ=x,因为弧FC=弧FC,所以∠FAC=∠FBC,所以tan∠FAQ= tan∠EBC=■=■,所以AQ=3x,CQ= AC-AQ=3■-3x,在Rt△CFQ中,由勾股定理得,x=■(舍)或■,在Rt△AFQ中,由勾股定理得AF=■.
法5:如图8,连接AO,过点F作FI⊥AO于I,作FK⊥BC于K,在Rt△BFC中,易得,FK=■,BK=■. 所以AI=AO-IO=AO-FK=■,FI=OK= BK-BO =■,在Rt△AIF中,AF2=AI 2+IF2=■,所以AF=■.
法6:如图9,过点A作AN⊥CD于N,作FK⊥BC于K,交 AN于P. 类似于法5,得AP=■,PF=■,所以AF=■.
2. 相似法
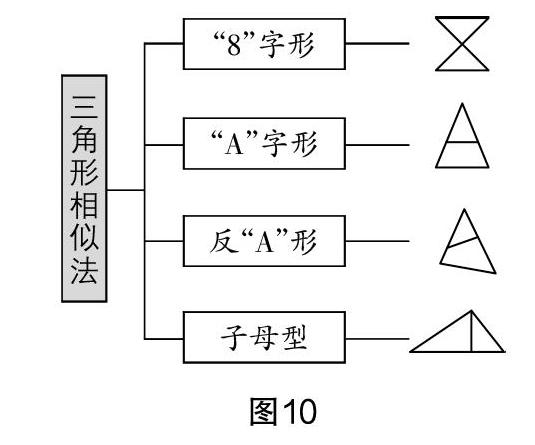
用相似法计算线段的长,则需要将该线段置于两相似三角形中. 而相似三角形不像全等三角形那么直观易找,但我们常说“万变不离其宗”,在试卷讲评过程中,可以让学生先回忆常见的相似模型,绘制成图10所示的思维导图,根据相似的几种基本模型来寻找思路. 当原图中没有基本模型时,可以考虑通过作辅助线构造出相应的模型.
法7:如图1,因为∠DAF=∠BEC,所以∠BAF=∠BED,又∠DBE=∠FBA,所以△ABF∽△EBD,所以■=■,得AF=■.?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇?摇
法8:如图11,连接CF,则出现子母型相似. BC2=BF·BE,CD2= DA·DB= BA·DB, 因为BC=CD,所以BF·BE= BA·DB,所以■=■. 又∠ABF=∠EBD,所以△ABF∽△EBD,■=■,得AF=■.
法9:如图11,设BF与AC交于点R,易得两组“8”字形相似,因为△BAR∽△CFR,所以■=■,得BR=■CR,又AR=3■-CR,在Rt△ABR中,由勾股定理得,AR=■,BR=■,又△ARF∽△BRC,所以■=■,AF=■.
法10: 如图12,过点D作DS∥AF,交BE的延长线于点S,过点D作DT⊥BS于点T. 因为DS∥AF,所以△ABF∽△DBS,■=■=■=■,所以ES=BS-BE=■-2■=■. 設ET=x,因为tan∠DET=tan∠BEC=3,则DT=ET·tan∠DET=3x,因为弧AB=弧AB,所以∠AFB=∠ACB=45°.
因为DS∥AF,所以∠S=∠AFB=45°,所以ST=DT=3x.又ET+TS=ES,所以4x=■,x=■,所以DS=■·TS=■,所以AF=■.
法11:如图13,连接AO交BE于点M,作AH⊥BE于点H. 易得△ABM∽△DBE,所以■=■=■,所以AM=2,因为sin∠AMH= sin∠BEC=■,所以AH= AM·sin∠AMH=■,所以AF=■AH=■.
3. 解析法
所谓解析法求线段长,是指将所研究的问题放在平面直角坐标系内,求出所求线段的端点坐标,再通过两点距离公式求出线段的长. 基于此,我们有如图14所示的几种思考.
法12:如图15,以BC所在直线为x轴,OA所在直线为y轴,建立平面直角坐标系. 则BE:y=■x+1,因为点F在⊙O上,所以设F(3cosα,3sinα),将点F坐标代入BE解析式,得3sinα= cosα+1,又sin2α+cos2α=1,所以sinα=■, cosα=■,F■,■,因为A(0,3),所以AF=■=■.
法13:如图15建立平面直角坐标系. 可求得直线BE的解析式为y=■x+1,直线CF的解析式为y=-3x+9,从而得两直线的交点F■,■,同法11,得AF=■.
教学启示
1. 在问题解决的过程中,恰当地运用思维导图,首先可以起到将零散的知识系统化的作用,如图2、图10. 在解题之前,我们往往先要重现学过的基本方法、基本模型,而思维导图的可视化功能可以使头脑中的记忆显性化,既是对所学知识的及时总结和提炼,又可以减轻解题过程的思维量,使得解题规律模型化. 图3的运用,通过捕捉和表达发散性思维,思维导图将大脑内部的过程进行了外部呈现,放大了大脑的本领,加强了大脑的思维能力. 图14将头脑中的化归过程显性化,使得解题的方向明确,加强了思维的条理性. 另外,若将以上几幅思维导图整合成一张大的思维导图,则有效地完成了本内容的笔记,使得学生对解决求线段长这类问题所涉及的方法、策略有了更深层次的认识,从而实现用方法指导实践(解题),从实践中总结规律,在一般规律中实现解题能力、思维发散能力的提升,进而实现问题解决的创新,达到培养高阶思维的目的.
2. 在当今信息化发展迅猛的年代,识记、理解等低阶思维学习的重要性在逐渐弱化,而培养学生具有分析、评价、创新等高阶思维能力的重要性正在得到提升,不论是课程标准的要求,还是社会发展的需要都要求学生具有终身学习、分析问题、解决问题、创造创新的能力. 在讲评本题的过程中,师生一起绘制思维导图,大胆猜想实践,教师在每一类方法中挑出一种方法细研,其他的方法交给学生讨论,或者互相教授. 在整个过程中,学生的兴趣得到激发、思维得到启发. 教师从一般的解决问题的方法入手,再具体到本题的应用上来,再在解题之后适时反思评价,形成解题经验和方法,符合用理论指导和实践探索的辩证统一. 通过这种科学的实践探索,能养成学生解决问题的良好习惯和一般方法,为培养高阶思维打下基础.

