站在核心素养的视角看立体几何问题的解答

◇ 甘肃 王二强

《普通高中数学课程标准(2017年版)》提出了高中数学核心素养,包括数学抽象、直观想象、逻辑推理、数学运算、数学建模、数据分析这六个方面.立体几何内容是考查直观想象、逻辑推理、数学运算等素养的有效载体.本文以2019年全国卷Ⅲ中一道立体几何问题的求解为例,就其中所考查的数学学科素养进行分析.

(1)证明：图2中的A,C,G,D 四点共面,且平面ABC⊥平面BCGE；

(2)求图2中的二面角B-GC-A 的大小.

图1

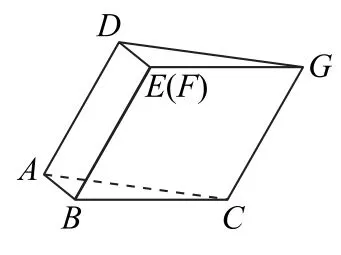
图2

立体几何与空间向量的解答题通常以棱柱、棱锥为载体,或通过将平面图形折叠为多面体进行考查.第(1)问一般考查空间中的平行或垂直关系的证明,第(2)问计算几何体的表面积、体积、空间角或空间距离.以空间角的求解为例,求解方法主要有定义法、向量法和面积投影法.本文利用这几种方法,从核心素养的视角,探究第(2)问的解法.

1 定义法

定义法,即利用平行、垂直原理构造空间角的平面角,利用解三角形的有关公式、定理求解.

解法1如图3 所示,取CG 的中点M,连接DM.因为DE∥AB,故由(1)知DE⊥平面BCGE,所以DE ⊥ME,所以△DEM 为直角三角形.由菱形BFGC 可知,BE＝2,∠FBC＝,所以EM ＝,又DE＝AB＝1,所以DM ＝＝2.又因为GM ＝,所以DM2＋GM2＝DG2,DM ⊥GC,所以∠DME 即为二面角B-GC-A 的平面角,所以,二面角B-GC-A 的大小为.

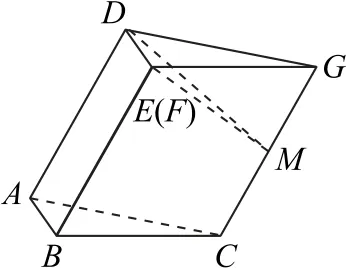
图3

2 向量法

向量法,即通过建立空间直角坐标系,利用直线的方向向量、平面的法向量之间的夹角来求解.此法是求解空间角问题的常用方法.

解法2取BC 的中点M,连接EM,由菱形BFGC 可知,BE＝2,∠FBC＝,所以EM ⊥BC,且EM ＝.由(1)知 平 面ABC ⊥平 面BCGE,所 以EM ⊥平面ABC.

以M 为坐标原点,建立如图4 所示的空间直角坐标系M-xyz,则A(－1,1,0),C(1,0,0),G(2,0,),所以

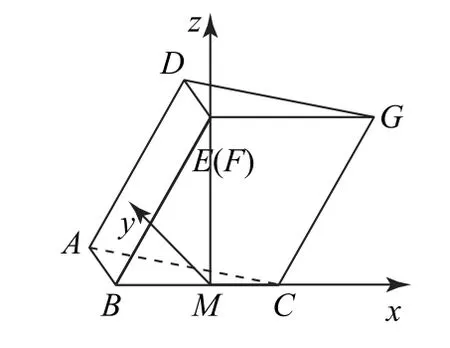
图4

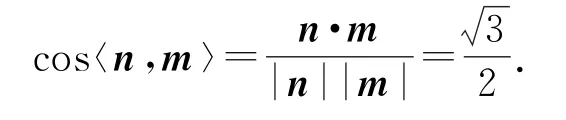
3 投影法

投影法是将构成二面角的两个面中的一个面投影到另外一个面上,利用投影面积与该面面积的比例关系与二面角的余弦关系进行求解.

解法3如图5所示,连接CD,CE,则所求二面角即为平面BEC 与平面ADC 所夹的角.

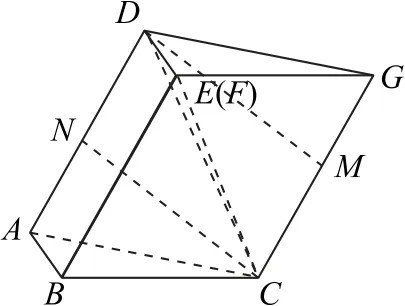
图5

因为AB⊥BE,AB⊥BC,所以AB⊥平面BCE,DE⊥平面BCE,所以△ADC 在平面BCE 上的投影为△BCE.取AD 的中点N,取CG 的中点M,连接CN,DM.由定义法可知CN ∥DM,CN ⊥AD,且CN＝DM ＝2,又AD＝2,所以△ADC 的面积为×2×2＝2.

总之,在立体几何与空间向量模块的备考中,要加强审题能力的培养,理清点、线、面之间的关系；强化解题的规范性,公式、性质、定理的运用要有理有据,关注逻辑的严谨性,作、证、求缺一不可,力求计算的准确性,避免出现会而不对,对而不全等现象.