流固耦合作用下空间导叶式离心泵叶轮湿模态分析

刘迎圆，宫建国，徐 颖，戎程锦，王乐勤

（1.上海师范大学 信息与机电工程学院，上海 200234；2.华东理工大学 机械与动力工程学院，上海 200237；3.浙江大学 化工机械研究所，杭州 310027）

0 引言

空间导叶式离心泵通常采用高而细的塔状结构，该结构可以节省空间，但容易发生振动[1]。当水力激振的频率与泵某一部件的固有频率相等或成比例时，会发生共振，严重影响结构的安全运行。研究表明，在流体介质的作用下，流体机械叶轮固有频率和振型均与在空气中有所差别[2]。因此，为获得流体介质环境下的叶轮模态行为并服务于后续的叶轮动力学分析，有必要研究流固耦合作用下空间导叶式离心泵叶轮的湿模态特性。

在离心泵等流体机械的湿模态分析中，目前主要集中在水环境下叶轮固有频率与附加质量效应的研究。例如，肖若富等[3]基于附加质量法从能量守恒的角度推导了水轮机转轮在空气和水环境下固有频率的关系。Egusquiza和Rodriguez等[4-5]采用试验和数值计算的方法，开展了水泵水轮机在静水中和空气中的固有频率的对比分析，结果发现在水中获得的振型与空气中相同，但固有频率会因水的附加质量效应而降低。张新和陈宇杰等[6-7]考虑流体的可压缩性研究了卧式轴流泵叶轮在水中和空气中的模态特性，发现水介质不仅会引起叶轮各阶固有频率的降低，还会导致各阶振型振动幅值有所减小。施卫东等[8]对特大型潜水轴流泵的轴系转动部件进行了湿模态分析，分析了不同情况下叶轮轴系转动部件模态行为的差异及其原因。尹庭赟和高海司等[9-10]分别对海水淡化增压泵和蜗壳式混流泵开展流固耦合模态分析，分析了叶轮结构及其材料属性对干湿模态固有频率的影响，结果表明金属材料的杨氏模量越大，叶轮各阶固有频率越大；且加厚后盖板厚度对提高各阶固有频率作用明显。综上，现有叶轮机械的湿模态分析中，水体模型多采用在叶轮周围包裹的水体模型（如圆柱形、方形水体），但这与实际流体域存在显著差异；同时，现有文献中尚未发现空间导叶式离心泵湿模态的研究工作。

基于此，本文以某空间导叶式离心泵为对象，考虑实际流体域的影响，开展流固耦合作用下空间导叶式离心泵叶轮的湿模态特性分析。主要包括考虑预应力的叶轮模态分析和静水介质下叶轮的湿模态分析：（1）首先通过求解Navier-Stoke方程（N-S方程）获取空间导叶式离心泵的流体作用力，进而基于流固耦合算法，研究预应力对叶轮模态的影响；（2）基于声-固耦合算法，开展水环境中叶轮湿模态特性研究，并分析流体介质参数对叶轮固有频率的影响，阐明不同介质中叶轮模态差异的原因；（3）结合叶轮动静干涉理论，分析叶轮的模态行为，预测叶轮的共振特性。

1 基本理论

叶轮结构的动力学方程为：

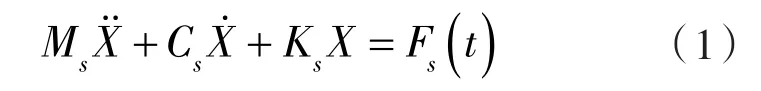
式中 Ms，Cs，Ks——结构系统的质量矩阵、阻尼矩阵和刚度矩阵；

F（st）——外界对结构的作用力，包括泵自身的重力、流体作用力和旋转产生的离心力。

叶轮干模态分析属于无阻尼模态分析，Cs=0，F（st）=0，动力学方程可简化为：

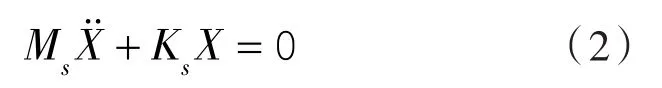
本文考虑水环境下叶轮的湿模态分析，其结构阻尼较小，忽略其对固有频率和振型的影响。同时，考虑液体对结构的耦合作用，假设液体介质为无旋、无黏、均匀的可压缩声学流体，则N-S方程可简化为流体的三维波动方程[6，11]：

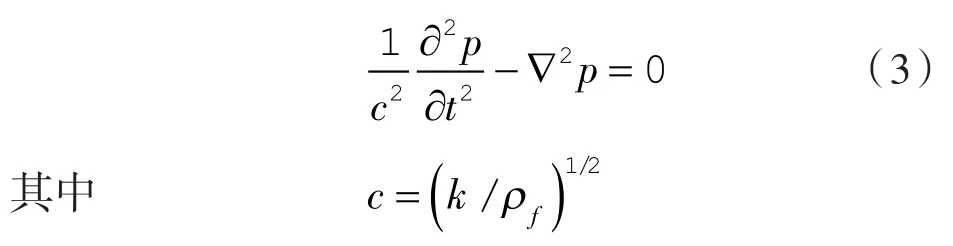
式中 c——流体声速；

p——流体压力；

k——流体压缩模量；

ρf——流体密度。

在流固耦合交界面，流体与结构之间的相互作用为：

式中 n——交界面处的法向量；

∇p——沿着法线向量的压力梯度；

将式（3）离散化，得流体的动力学方程：

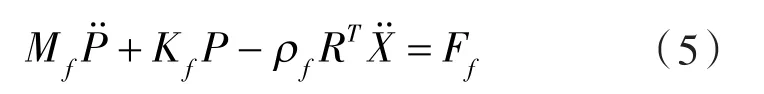
式中 Mf——流体质量矩阵；

Kf——流体的刚度矩阵；

P——流体声学压力；

R——流体和结构耦合矩阵；

Ff——作用在流体上的外力。

考虑声学流体介质的作用，结构的动力学方程可表示为：

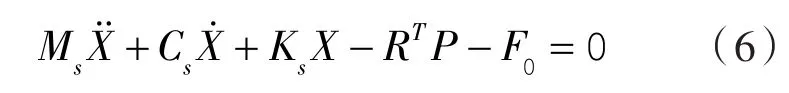
式中 Fp（t）——耦合面上声压在结构上的面力向量；

F0——作用在结构上的流体载荷。

对流体（声）-结构耦合系统来说，联立式（5）和式（6）即可得到结构声场耦合的方程：

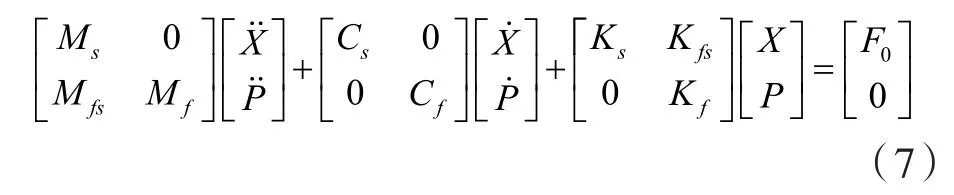
式中 Mfs——等效耦合质量矩阵；

Kfs——等效耦合刚度矩阵。

2 数值模型的建立

2.1 叶轮几何模型

空间导叶式离心泵的几何模型如图1所示，主要包括喇叭入口、叶轮、空间导叶和出口管路4个部分。泵的比转速为158，其主要运行与结构参数包括：叶轮出口直径D2=720 mm，叶轮叶片数Z=6，导叶叶片数M=7，设计流量Q=2 860 m3/h，设计扬程H=55 m，转速n=990 r/min。水泵叶轮材料采用具有耐腐蚀性的不锈钢0Cr18Ni9（S30408），其密度为 7930 kg/m3，弹性模量为 2.04×1011Pa，泊松比为0.3。

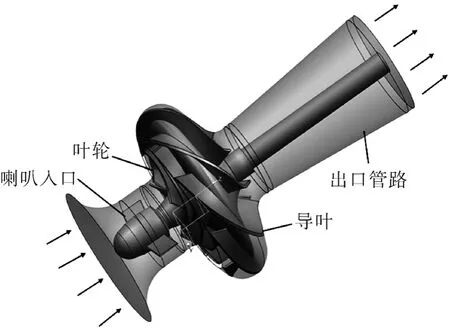
图1 空间导叶式离心泵几何示意

2.2 考虑预应力的流固耦合模型

采用Block Lancos方法对空间导叶式离心泵进行模态分析。离心泵结构域中，叶轮与轴作为整体考虑，主要约束为叶轮中心轴轴承支撑处的圆柱约束。叶轮轴系结构的主要约束与载荷如图2所示，叶轮预应力包括叶轮自身的重力、旋转产生的离心力和水体作用于叶片和轮毂、盖板等部分的压力。叶轮自身重力与旋转时的离心力可通过施加重力加速度和旋转速度设定。水体作用于叶轮上的压力则是基于单向流固耦合的方法，首先通过CFX软件采用有限体积法对流体流动控制方程进行离散求解，获取流体作用力后通过流固耦合面施加到叶轮轴系结构上。

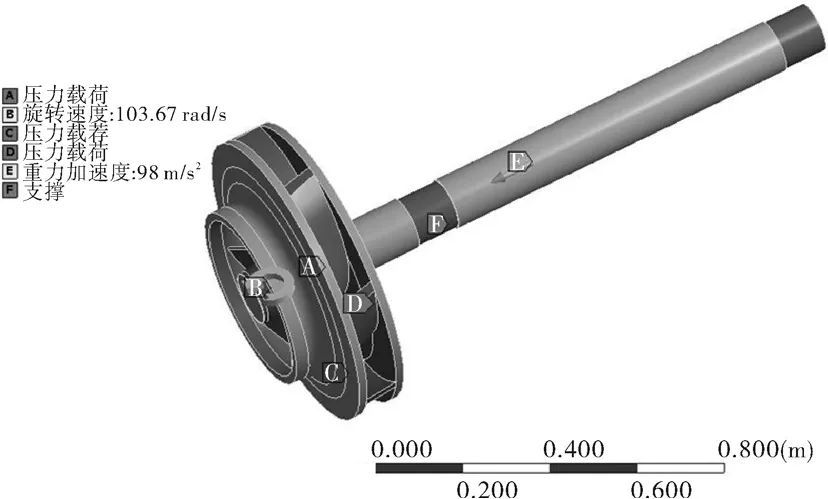
图2 有预应力叶轮与轴结构的约束设置

流体预应力计算时，采用六面体网格对泵的水力模型进行离散如图3所示，叶轮与导叶的单元数分别为4 192 440和5 053 356，全流道总网格单元超过107。另外，为了保证足够的求解精度，叶轮和导叶的无量纲y+值分别为90与50。采用RNG k-ε湍流模型进行控制方程的封闭求解，主要边界条件为质量进口、压力出口，近壁面采用标准壁面函数处理。

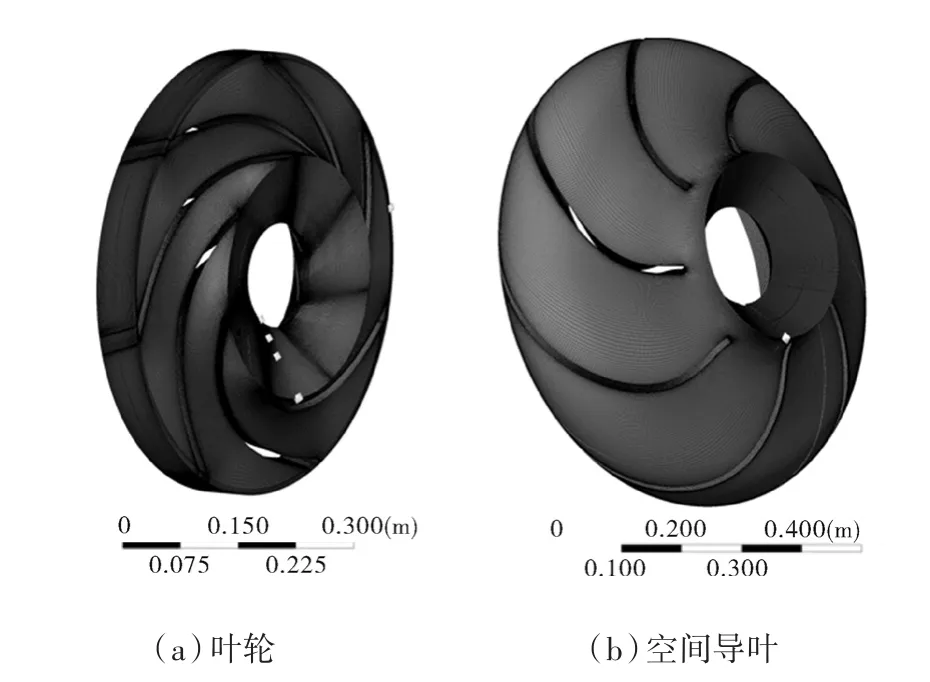
图3 流体预应力计算的叶轮与导叶流体域网格

2.3 基于声固耦合算法的叶轮湿模态模型

基于声固耦合算法，考虑流体的可压缩性，对空间导叶式离心泵开展无预应力的湿模态分析。离心泵的结构域和水体域网格如图4所示，结构和流体单元分别采用高阶单元SOLID186和FLUID221，结构和水体的网格单元数分别为107 096和191 459，节点数分别为180 757和282 042。

图4 叶轮结构与水体部分的网格

水体模型通过Workbench中的Acoustic body设置为声学流体，并将叶轮叶片及其前后盖板内表面设置为流固耦合面。同时，为了模拟叶轮在水域的运转状态，水域进口设置为自由液面，出口设置为带压面，压力为537.922 kPa（扬程55 m）。

3 结果与分析

3.1 叶轮预应力求解

流体载荷采用稳态计算，计算得到的离心泵扬程与效率如图5所示。可以看出，离心泵的扬程与效率的计算值均与试验值较为接近，这说明文中的数值模型较为准确。

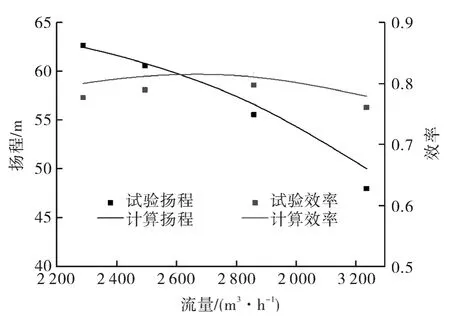
图5 泵外特性曲线

基于上述模型，计算叶轮表面的流体作用力后，通过Workbench流固耦合程序施加到叶轮流固耦合界面上，可得到预应力下叶轮的等效应力和叶轮变形如图6所示。可以看出，叶轮的等效应力最大值集中在叶片与轮毂相接的根部，叶轮与轴的连接处、叶轮前后盖板等效应力均较小。与未变形结构相比，叶轮表现为相对于轴的弯曲变形，并由叶轮进口处向叶轮出口扩展。综合考虑叶轮轴系等效应力和变形的情况可知，如果需要增强系统的结构刚度，应该从叶片与前后盖板连接处和轴的刚度入手。

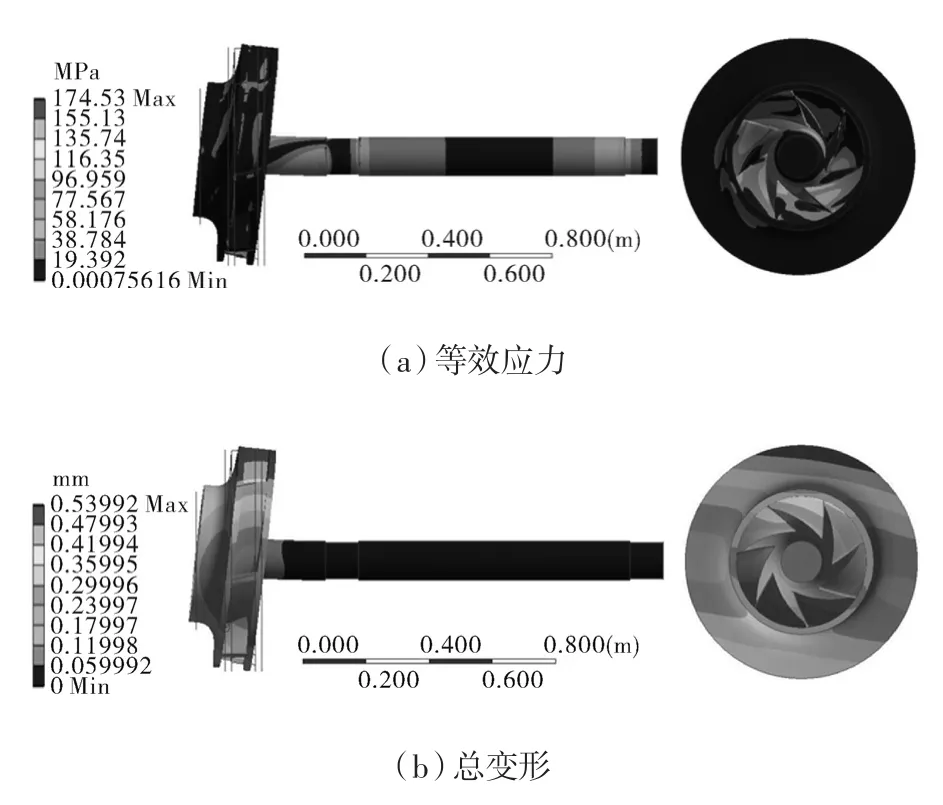
图6 预应力作用下叶轮的等效应力与变形分布（990 r/min，黑色边框为未变形结构）

3.2 预应力作用下的叶轮模态分析

有无预应力作用下叶轮的前6阶固有频率见表1。可以看出，有无预应力作用下叶轮不同阶次的固有频率有所差别，但是相差不大。同时，采用增大泵转速的方法使预应力增大，研究预应力的进一步影响。结果发现，当预应力增大到原来值的6倍后，考虑预应力下的固有频率仍未有较大变化，变化率均在1.8%以内（见表1）。这说明，叶轮结构在预应力的作用下并未出现明显的应力刚化，同时流场作用力以及惯性力对叶轮固有频率的影响并不明显。

表1 有无预应力作用的叶轮固有频率对比 Hz

预应力作用下叶轮的前6阶振型如图7所示。图中采用节径ND（Nodal diameter）的数目i和节圆NC（Nodal circle）的数目j表示叶轮的振型（i，j），如图7中1阶模态（0，1）代表该叶轮振型中包含0个位移为0的线和1个位移为0的圆。可以看出，在共振频率作用下，空间导叶式离心泵叶轮的振型主要有3类，分别为：弯曲振动模态、旋转振动模态和轴向振动模态。

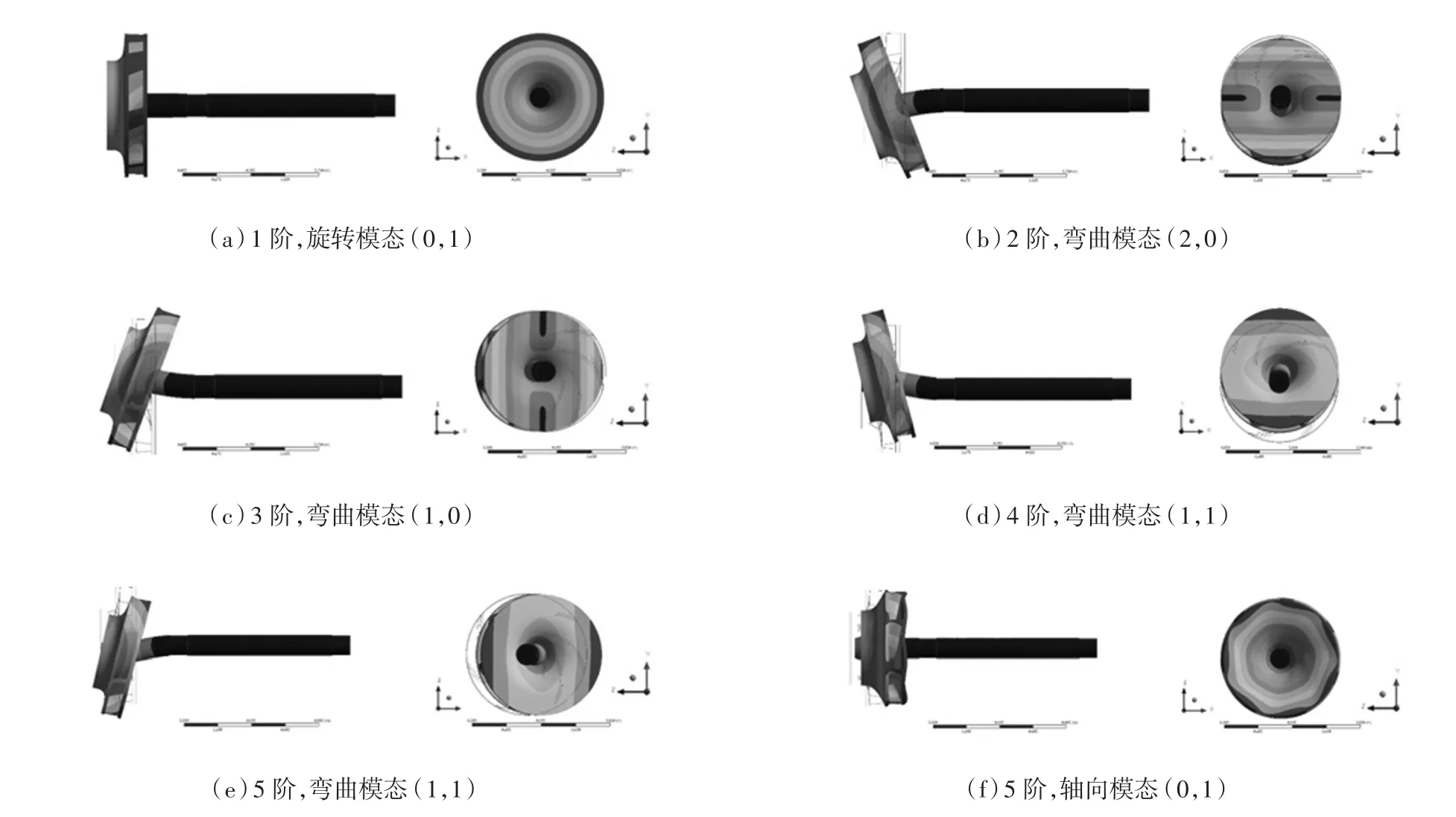
图7 有预应力作用下叶轮的前6阶振型（黑色边框为未变形结构）

3.3 叶轮湿模态分析

固有频率下降率（FRR）是用来描述液体介质对叶轮结构固有频率下降的影响[12-18]，如下式所示：

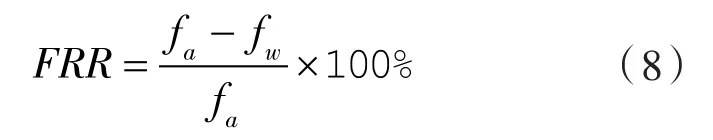
式中 fa——叶轮的固有频率（干模态）；

fw——叶轮的固有频率（湿模态）。

同时，本文采用无量纲量附加质量系数l描述水体的附加质量见下式:

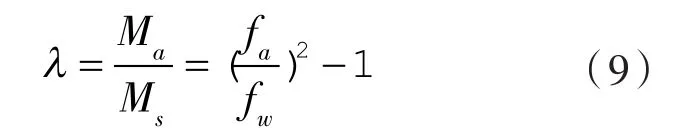
式中 Ma——附加质量矩阵。

叶轮在水环境下的前6阶固有频率及其下降率和附加质量系数见表2。可以看出，水环境下叶轮各阶次的固有频率均大幅降低，除第三阶固有频率下降率为33.81%外，其他阶次下的叶轮结构固有频率下降率达约60%～65%左右。相应地，水体附加质量系数除第三阶次为1.28外，其它均在5.21～7.26范围内。这说明，相对于干模态而言，水体的附加质量效应较大，而水体刚度与结构刚度相比可以忽略，故水环境下叶轮的固有频率下降。

表2 水环境下叶轮的固有频率及下降率

叶轮湿模态下的前6阶振型如图8所示。可以发现，在湿模态共振频率作用下，离心泵叶轮的振型主要有两类：弯曲振动模态和旋转振动模态。与干模态叶轮振型相比如图7所示，湿模态下的叶轮振动幅值有明显较小的趋势，这说明水体的附加质量和附加阻尼对叶轮的振动产生了抑制作用。

为了进一步分析流体特性对叶轮湿模态的影响，本文对不同流体特性参数下叶轮模态开展相应的分析。流体密度与声速对叶轮湿模态下固有频率的影响如图9所示。可以看出，流体环境下，叶轮固有频率主要取决于流体介质声速，而受流体介质密度的影响较小；同时流体介质的声速越小，叶轮湿模态下的固有频率越小。这是由于在湿模态分析中，流体介质被假设为声学流体，流体的附加质量与其声速的大小密切相关。流体介质的声速减小，流体的附加质量增大，叶轮的固有频率减小。考虑到气液两相介质的相互掺混会改变流体流动的结构特征，使流体声速大幅降低，故高参数化（高转速、高水头等）流体机械的湿模态分析，应当考虑空化气液两相流动等因素的影响。

图8 叶轮水环境下的湿模态前6阶振型（黑色边框为原模型位置）

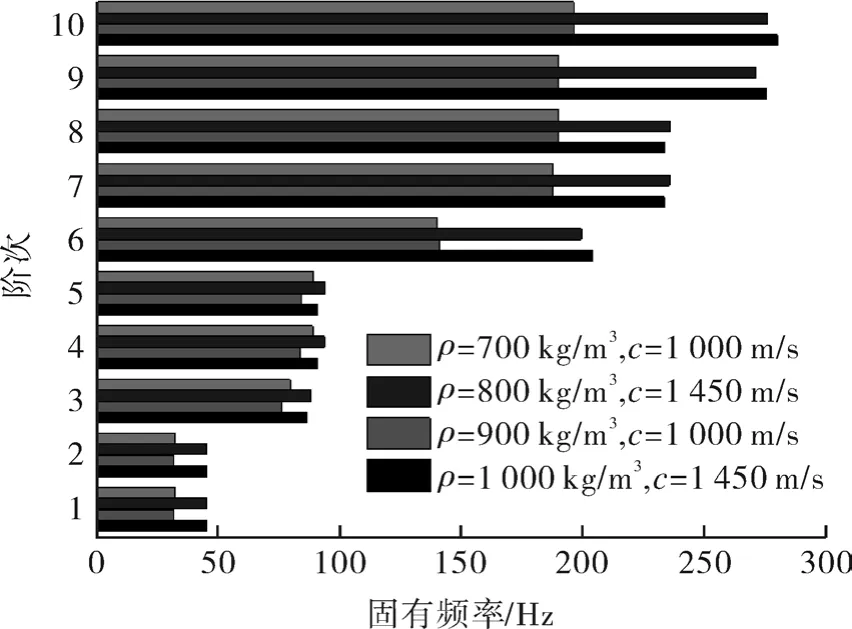
图9 不同介质参数环境下叶轮的固有频率

3.4 动静干涉原理及叶轮共振特性分析

叶轮与导叶的动静干涉是流体机械叶轮以及静止部件的主要振源[16-17]。在动静干涉作用下，叶轮的激振频率与导叶等静止部件的激振频率分别为：

式中 fr——叶轮的激振频率；

Zg——导叶数；

fs——导叶等静止部件的激振频率；

Zr——叶轮叶片数。

而激振力的振型由叶轮叶片数和导叶数决定[18]。本文模型泵的激励力与振型见表3。一般来说，k值较小的振型容易被激励出来，因此表3中给出了|k|＜10的振型，其中k=-1和k=-2更加容易被激励出。

式中 k——振型中的节径数目。

表3 激振力频率及振型（|k|＜10）

由表3可以看出，叶轮最小的激振力频率为115.5 Hz，其与结构干模态和有预应力的一阶固有频率非常接近，此时容易诱发叶轮共振。但考虑到水体作用下叶轮湿模态固有频率有所降低，激振力频率与固有频率不再相近，进而抑制了叶轮共振模态的激发。

4 结论

（1）预应力对叶轮的固有频率影响不大，表明叶轮结构在流体作用力、旋转离心力和自身重力的作用下并未出现明显的应力刚化。

（2）水环境下，叶轮各阶固有频率均大幅降低，叶轮振型的振动幅值有所减小。这是由于水体会在叶轮的运动下产生协同振动，引起水体的附加质量效应和阻尼作用，振动能量向外辐射，造成固有频率和振动幅值的下降。

（3）叶轮固有频率主要取决于介质的声速，而受介质密度的影响较小。同时，介质的声速越大，叶轮湿模态下的固有频率越小。这是由于在湿模态分析中，流体被假设为声学流体，流体的附加质量与介质声速密切相关。考虑到气液两相介质的相互掺混会降低流体声速，故高参数化（高转速、高水头等）流体机械的湿模态分析应该空化两相流动等因素的影响。

（4）离心泵动静干涉的激振力频率分析发现，叶轮的最小激振力频率与结构干模态、含预应力条件下的一阶固有频率非常接近，容易诱发叶轮共振。但考虑到水体作用下叶轮湿模态固有频率有所降低，激振力频率与固有频率不再相近，进而抑制了叶轮共振模态的激发。