基于GARCH-MIDAS模型对股市波动率预测

刘国山， 王 璐， 刘 亚

（西南交通大学数学学院，成都 610031）

股市波动率不但在金融监管、投资组合选择和风险管理等领域起着至关重要的作用，并且也影响着广泛投资人的决策. 金融市场的剧烈波动强大的溢出效应对经济运行产生了巨大影响，因此监管机构极力避免剧烈的市场波动，学者们也十分重视对股票市场波动率的研究. 在现有的文献中，最常使用的实证模型是由Bollerslev［1］最早提出的广义自回归条件异方差（GARCH）模型. 然而Ghysels 等［2］发表的一份颇具影响力的论文表明：由于GARCH 族模型严格受到数据频率的限制，它们并不适用于探究长期资本市场的波动性.相反，Engle等［3］提出的GARCH-MIDAS 模型有着优于传统模型的表现. 该模型将波动率分解为两个部分：短期波动和长期趋势. 短期波动包含了GARCH 过程捕获的高频波动，长期趋势包含了GARCH 过程捕获的低频波动. 由于GARCH-MIDAS模型能够克服金融变量因为不同抽样频率导致的复杂性，该模型在实证预测中被Pan等［4］广泛采用.

然而标准的GARCH-MIDAS模型对股市波动率的解释仍存在一定的缺陷. 首先，它在短期的预测中只采用简单的GARCH（1，1）模型，这使得该模型无法适应金融市场的一些较为典型的现象，如杠杆效应，超峰态和波动聚集［5］等. Liu等［6］的研究结果表明有必要对GARCH 模型各种变体的预测准确性进行深入评估，许多研究将非对称效应纳入了股票波动率预测模型中. Pan 和Liu［7］等相关研究都表明考虑非对称效应的GARCH 模型表现优于一般的GARCH 模型. 因此，我们并不只用标准GARCH 模型对波动率中的短期成分进行拟合，而是运用更复杂的GARCH 族模型，如GJR-GARCH和EGARCH模型.

另外，GARCH-MIDAS模型无法解释极端事件的影响，而理解极端事件的冲击有助于解释市场波动性.当事件发生时，比起小的股价波动，人们更关心大的股价波动，一系列外生变量，如局部战争，政治事件和金融危机等会使市场波动加剧. Schwert［8］的研究表明无论用月收益率、日收益率还是每15分钟的收益率进行衡量，市场压力都会伴随着高强度的市场波动，例如1987年的股市崩盘和2007年的次贷危机，因此极端事件与极端波动是紧密相关的. 根据Jacob［9］的研究，GARCH 模型的预测性能可以通过加入极值估计量得到提升. 因此本文将极值效应纳入模型设计中.

综上，现有文献中关于非对称效应和极值效应对股市波动，特别是中国股市波动影响的研究存在不足.而由于非对称效应和极值效应均在股市波动率预测中有着重要作用，本文对GARCH-MIDAS模型进行修正，将两种效应纳入修正后的模型中. ①采用了更为复杂的GARCH族模型来刻画金融市场的特殊现象. 我们采用GARCH、GJR-GARCH和EGARCH模型来拟合GARCH-MIDAS模型中的短期波动. 如GJR-GARCH模型［10］和EGARCH模型［11］等模型在Hou和Suardi等［12］的研究中已被证明具有良好的样本外预测能力；②其次，我们探讨了极端冲击在波动率预测中的重要性. 与现存的大多研究类似，我们将以超过某些临界值的阈值为准，来识别极端波动率，基于Huang和Arısoy等［13］的研究，我们使用收益率的经验分位数来确定阈值. 与以往的研究只关注极端冲击的整体影响不同，我们将极端值变化分解为两部分：极端正冲击和极端负冲击. 显然我们的扩展模型不仅可以描述大的“好消息”而且可以描述大的“坏消息”对股价波动的影响.

1 模型设计

1.1 GARCH-MIDAS模型

在研究股票波动问题上，现有方法大多都是用月度或是季度数据来构造模型，或是降低股市数据频率.这样做容易丢失股市中的高频有效信息，使得参数估计和波动率预测有所偏差［14］，Ghysels［2］和Pettenuzzo等［15］率先提出了混频的抽样模型（MIDAS），Engle等［3］进一步将MIDAS运用到广义自回归条件异方差模型中，提高了参数估计的有效性和波动率预测的准确性.

假设ri,t是t 月i 日的对数收益率，该GARCH-MIDAS模型中的收益率和波动率的描述如下：

其中：α>0;β>0;α+β<1. 此外，长期趋势tt受已实现波动率RV的影响，具体形式为：

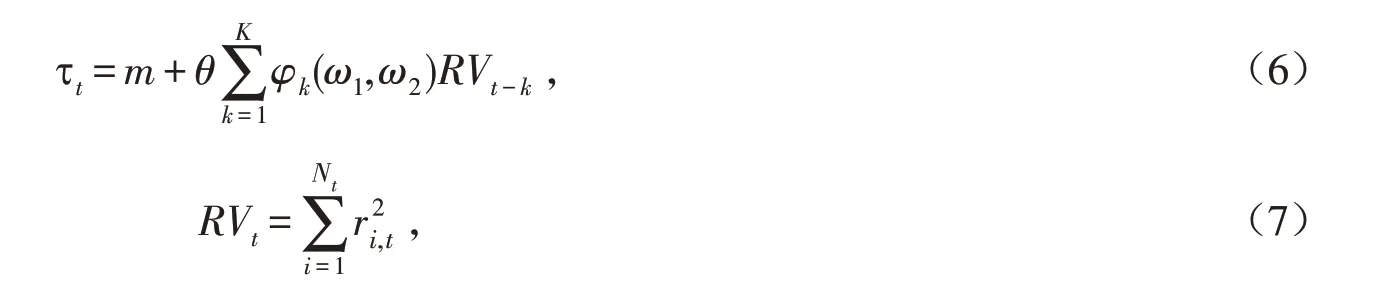
其中：μ，ω，ω1，ω2，m，θ 均为待估参数；RVt由每月的日收益率平方和计算得出；K为低频变量的最大滞后阶数，根据engle［3］和asgharian等［4］的研究，本文选用K=24. φk(ω1,ω2)表示β 型滞后变量的权重函数，因为β 多项式更加灵活［16］. 因此我们假定在表达式（6）中的权重函数为β 型函数：

一般固定ω1=1，为了保证滞后变量的权重呈衰减形式（距离当期越近，对当期的影响就越大），由系数ω2来决定低频数据对高频数据影响程度的衰减速度. 此时，Beta权重函数简化为：

其中：α，β 为待估参数，根据收益率的分布函数和模型设定，用极大似然估计得出所需参数，极大似然函数为：

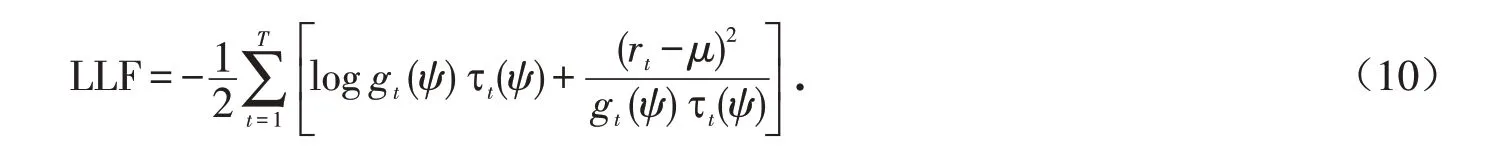
1.2 扩展的GARCH-MIDAS模型

继Cont［17］之后，一些GARCH类模型都具有描述波动聚集性、无限持续性和非对称杠杆效应的能力. 因此，在标准的GARCH-MIDAS模型中，尽管短期波动gi,t采用GARCH（1，1）模型在某些情况下对股票价格有较好的拟合效果，但我们尝试采用更复杂的GARCH 型模型来对短期波动进行拟合，包括GJR 和EGARCH.另外为了探讨加入极端冲击是否可以改善对股票价格波动的预测. 为此我们在各种GARCH-MIDAS 模型中加入了极端冲击. 基于Huang［15］的论文，为了研究极端冲击对波动率预测的影响，我们对表达式（6）中的长期趋势进行了如下修正：

模型1：GJR-GARCH-MIDAS模型

我们使用GJR（1，1）模型［11］来代替等式（5）中的GARCH（1，1）模型，以便更进一步研究股票收益率波动中非对称效应.

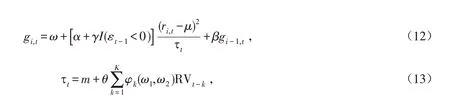
其中：I()代表指示函数，γ 代表非对称杠杆系数，可以捕捉非对称效应. 这里I(⋅)=1 或是I(⋅)=0，其余的参数定义同章节1.1一致.

模型2：EGARCH-MIDAS模型

指数GARCH 模型（EGARCH）是由Nelson［12］提出的一个非线性的GARCH 类模型. 这里用EGARCH 来代替GARCH（1，1）模型：

这里的参数定义与式（5）和式（11）一致.

模型4：GJR-GARCH-MIDAS-ES模型

为了考虑非对称效应和极端冲击的共同影响，我们在GJR-GARCH-MIDAS 模型（即模型1）中的长期趋势中加入极值影响. 其表达式如下：

其中：参数与式（12）和式（11）定义一致.

模型5：EGARCH-MIDAS-ES模型

EGARCH-MIDAS-ES 模型是EGARCH-MIDAS 模型（即模型2）的扩展，它研究了对数条件波动率的动态变化. 我们在扩展的模型中加入了长期波动率受到的极端正冲击和负冲击的影响. 模型5的定义为：

这里参数与式（14）和式（11）定义一致.

2 数据与描述性统计

上证50指数挑选上海证券市场规模大、流动性好的最具代表性的50只股票组成样本股，反映了上海证券市场最具影响力的一批龙头企业的整体状况，对其进行比较准确的预测，将会有很重要的经济意义［19］. 本文选取上证50指数自2004年1月5日到2019年6月28日的收盘价共3762个样本数据. 我们将整个数据集划分为样本外和样本内两个数据集，样本内数据集包含2004年1月5日到2013年9月16日共2355个数据，样本外数据包含从2013年9月17日到2019年6月28日共1407个数据. 所有数据均来自锐思数据库，股市收益率为收盘价格的自然对数差分形式，并且扩大了100倍. 收益率计算公式为：

其中Pi,t表示t 月i 天的收盘价.

图1 收益率和波动图Fig.1 Trend charts of returns and volatility

图1是上证50指数的收益率时序图和波动图，这里波动采用收益率的平方代替. 从图1可以看出，收益率表现出很强的自相关性，当收益率的自相关系数有很强的持续性并且无显著的平滑衰减时. 标准的Garch模型可能无法有效地拟合波动率走势，因为波动率具有明显的期限特征，并受到长短期不同成分的影响［20］，因此对波动率进行长短期分解有助于波动率的建模和预测.

表1给出了上证50收益率的描述性统计. 由表1可得，样本均值接近零，但收益率的相应方差较大. 回归具有负偏斜，意味着该序列左尾比右尾更长，即极端损失比极端收益出现的概率更大. Jarque-Bera 统计数据表明收益率具有显著的非正态分布. ADF检验结果表明，在1%显著性水平下，拒绝原假设，认为该收益率序列平稳，可以直接建模而无须进一步变换.

表1 收益率的描述性统计Tab.1 Descriptive statistics of returns

3 实证结果分析

3.1 模型估计

图2是真实波动与预测的条件方差走势图，其中真实波动用收益率的平方代替. 表2为所有模型的极大似然估计结果及相应的渐进标准误差. 表中大多数参数均显著，这表明我们研究的混合数据样本模型框架非常适用于股票收益率的拟合. 首先，GARCH系列模型的参数（μ，α，β）在统计意义上都是显著的，这表明上证50收益率在短期波动上具有强烈的波动聚集效应. 其次，所有估计的α+β 之和均小于1，但都接近于1，这表明波动率存在较高的持久性，这与Engle和Rangel［21］的研究结论一致. 同时，除模型4以外，所有模型的估计值α都显著大于0，表明过去的信息提升了股票收益率的波动性. 再次，参数γ 在模型2（EGARCH-MIDAS）、模型4（GJR-GARCH-MIDAS-ES）和模型5（EGARCH-MIDAS-ES）中均显著大于0，即非对称效应在这些模型中均存在. 这表明，负面冲击对股票收益的短期波动性的影响比正面冲击更甚［22］.

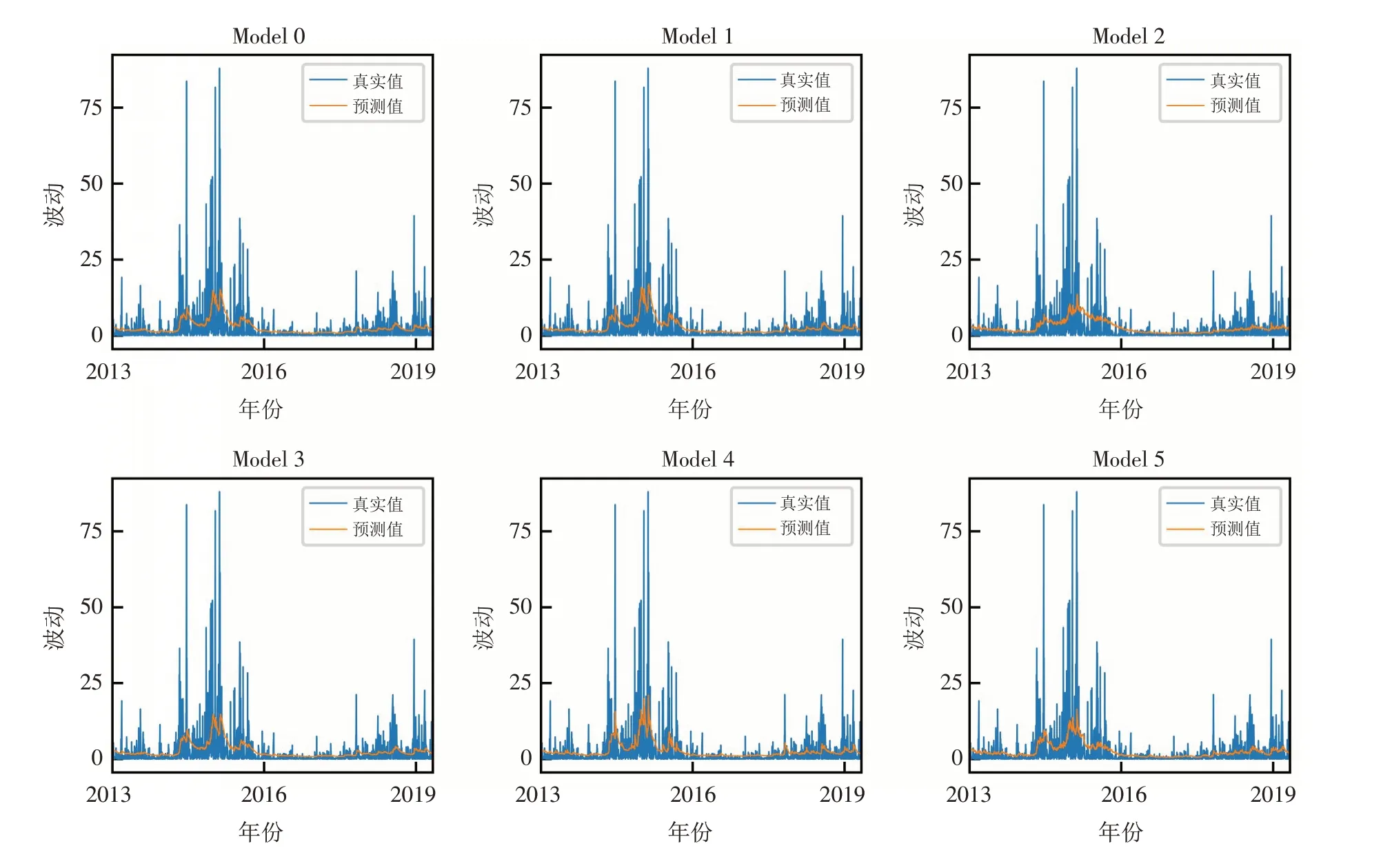
图2 真实波动和预测波动走势图Fig.2 Trend charts of real and forecast volatilities

表2 参数估计结果Tab.2 The estimation results of parameters

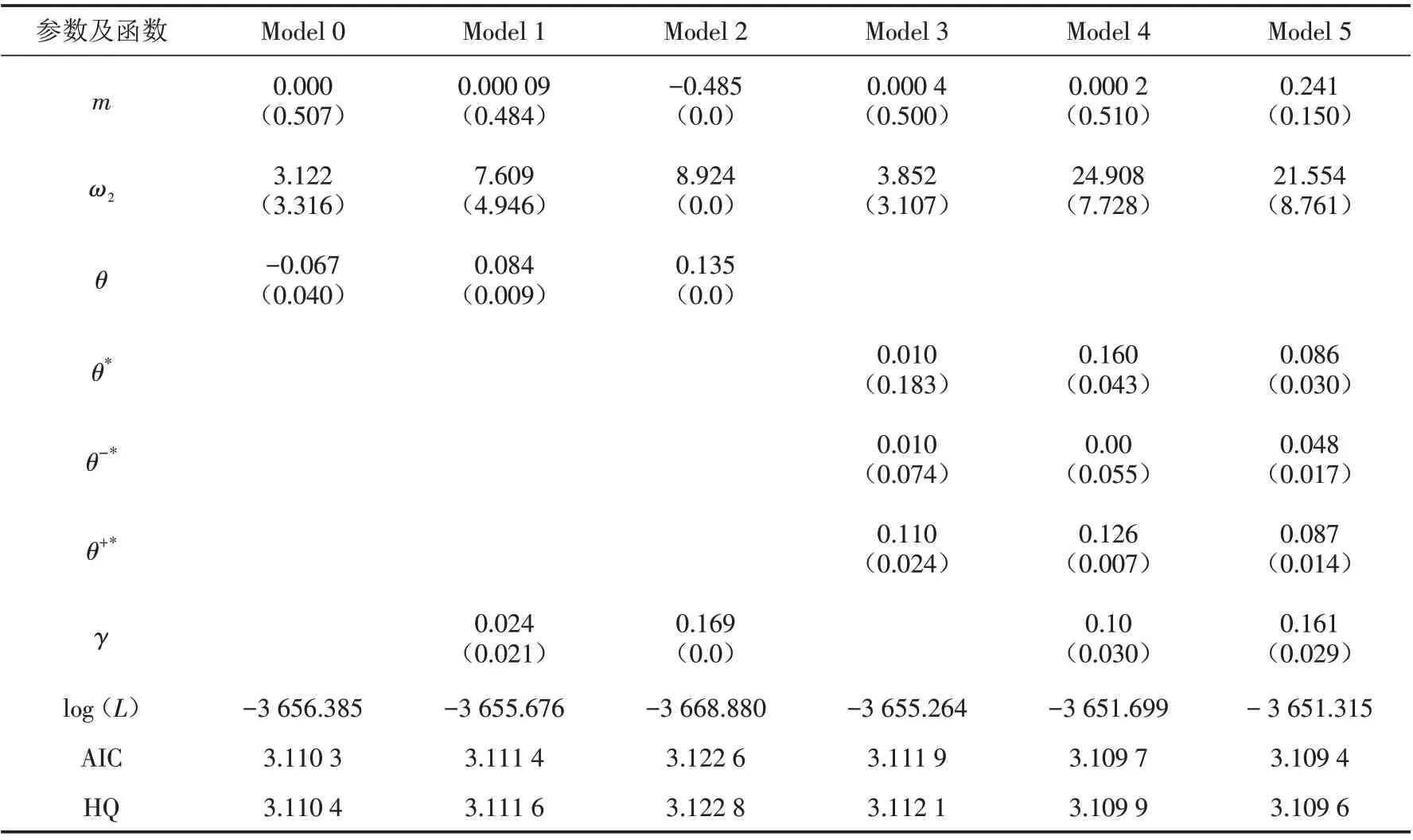
续表

此外，我们发现θ-*，θ+*和在所有模型中均大于0，这证实了极端冲击对股票收益的波动具有强烈影响，这表明极端影响可能是股票持续波动的根源［23］.

诊断性检验使用了对数似然（log（L）），Akaike 信息标准（AIC）和Hannan-Quinn 信息标准（HQC）三种标准. 以log（L）为准，模型5（EGARCH-MIDAS-ES）的log（L）值最大：以AIC 和HQC 为准，模型5 的AIC值和HQC 值均为最小. 这表明，从本文使用的检验标准来看，模型5 对于股票收益波动的样本内拟合效果最佳.

3.2 样本外预测

本文参考尚玉皇和郑挺国［24］的方法，首先得到样本内的估计值，而后计算样本外的日波动率的预测值，再根据预测均方误差（MSE），预测绝对误差（MAE）和（QLIKE）三种损失函数来计算预测的评价标准.

但是，很难肯定地说损失值最小的模型就一定明显优于其他模型. 因此，我们采用了Hansen等提出的模型置信集［26］（MCS）测试. 与SPA测试相比，MCS测试不需要指定基准. MCS检验从所有模型中顺序删除性能最差的模型，直到在α显著性水平上不再拒绝相等预测准确度（EPA）的零假设，然后存活下来的模型集合构成了MCS. Liu等［27］的研究表明，将阈值设置为0.10更有助于挑选出最佳的模型. 从表3列出的MCS检验结果来看，对于损失函数MSE，所有扩展模型对应的p 值均大于0.10，这表明这些扩展模型相较于标准GARCH-MIDAS模型而言有更好的预测效果. 如果对三个损失函数同时进行考察，则只有模型3、4和5的p 值均大于0.1，并且模型5的p 值远高于其他两个模型.

表3 MCS检验Tab.3 MCS tests

另外，采用DM检验来比较标准GARCH-MIDAS模型和扩展模型之间的预测准确性，以标准GARCH-MIDAS模型为参照，使其和5个各扩展模型分别进行比较. 该检验的原假设为：两种预测方法的预测准确率的差异在统计学上不显著. 在本文中，拒绝原假设意味着预测值之间存在显著差异且扩展模型的预测误差显著小于标准模型的预测误差，即扩展模型的预测表现更佳. 表4展示了MSE，MAE和QLIKE 3种标准下DM检验的结果. 检验结果显示，模型5（EGARCH-MIDAS-ES）的预测准确性与标准模型有显著差异，并且损失比率小于1，意味着模型5的表现显著优于标准模型.

表4 DM检验Tab.4 DM tests

总的来说，各项检验的结果表明，相较于标准GARCH-MIDAS 模型和其他扩展模型而言，模型5（EGARCH-MIDAS-ES）在样本内拟合和样本外预测上表现都比较好. 这表明在GARCH-MIDAS 族模型的构建上，考虑短期波动中的非对称效应和长期趋势中极端冲击能够有效提高波动率预测的准确性.

3.3 稳健性分析

本节将通过两方面来检验扩展模型预测能力的稳健性：①更换MCS检验的波动率阈值；②更换子样本.

不同的波动率阈值选择会导致实证结果的不同，因此选择合适的波动率阈值对于评估我们模型的预测能力有着重要意义. 为了验证预测结果的稳健性，我们新增了两个阈值的选择：①δ1=0.08，δ2=0.92；②δ1=0.12，δ2=0.88. 表5展示了不同阈值下MCS检验的结果. 该结果与表3中得到的结论相近，模型5依然有着优于标准模型和其他扩展模型的表现.

表5 MCS 检验（不同阈值）Tab.5 MCS tests（Different thresholds）

研究高波动时期模型对波动率的预测能力也很有价值，所以我们特别关注了2016年和2017年波动幅度较大的两年. 表6展示了这两年的MCS检验结果，从中可以看出模型5的表现始终是最佳的.

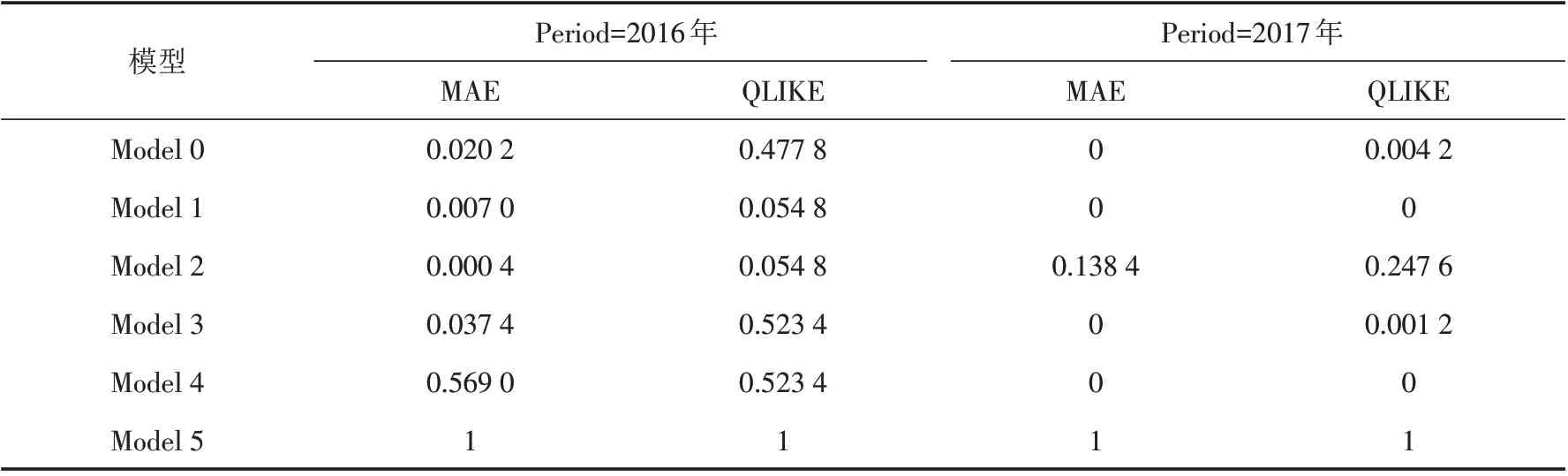
表6 MCS检验（高波动时期）Tab.6 MCS tests（High volatility period）

4 结论

虽然股票波动率预测的研究已经很充分，但是，关于极端冲击对波动率影响的研究还很少. 在本文中提出了5种GARCH-MIDAS 模型的增强模型，以期对非对称效应和极值效应进行更好的捕捉. 为了探究新模型的预测表现，我们对上证50的波动率进行了预测.首先，样本内的结果表明，在本文提出的GARCH-MIDAS族模型框架下，非对称效应和极值效应对股票价格波动有着显著影响. 总之，非对称效应和极值效应是造成股价波动高持续性的两个重要因素. 其次，在样本外预测中，从3个损失函数还有DM和MCS检验的结果来看，非对称-阈值模型的表现显著优于标准模型，能对股票波动率进行更好的预测. 最后，稳健性检验的结果显示本文的预测结果在更换预测时期和波动率阈值的情况下依然稳健. 本文的主要贡献在于更加广泛地探讨了GARCH-MIDAS 族模型在股票收益率波动率方面的预测效果，同时将非对称效应和阈值效应纳入模型框架中，从而提高了波动率预测的准确性.我们的研究为股市波动率预测提供了新的见解.