一类具有Allee效应的偏害系统的稳定性分析

石志高

(福建江夏学院 数理教研部， 福建 福州 350108)

0 引 言

种群偏害关系是生态系统中种群间普遍存在的一种关系， 其主要特点是当两个种群生活在一起时， 一个种群对另一个种群起到抑制作用， 而自身却不会受到影响．如胡桃树分泌一种叫做胡桃醌的物质， 它能抑制其他植物的生长.因此， 在胡桃树下的土表层中是没有其他植物的.Allee于1931年提出， 当种群密度过低时， 生物会出现寻找配偶的困难， 以及其他社会功能的紊乱等， 导致物种的增长率下降， 这一现象将随着物种种群数量的增加而逐步减缓并最终消失， 称为Allee效应.种群的Allee效应在很大程度上将增加种群灭绝的可能性， 会对生态学系统的稳定性产生影响， 是广大学者关注的焦点[1-7]， 但是当前对具有Allee效应的两种群偏害、 偏利合作模型[8-12]的研究较少.祝占法等[8]研究了一类更为广泛的偏害系统

(1)

所有参数均为正常数， 作者对系统(1)进行了定性分析. Guan Xinyu[9]研究一类具有偏利共生系统

(2)

(3)

式中：a1,a2,b1,b2,c1,d1,y均为正常数.作者研究了该系统的正平衡点的全局稳定性.并指出Allee效应不改变种群的平衡位置和稳定性， 但没有对系统进行数值仿真以验证相关结论．受上述启发， 本文考虑一类第二种群具有Allee效应的偏害系统， 探索Allee效应对系统正平衡点的全局稳定性的影响， 系统如下

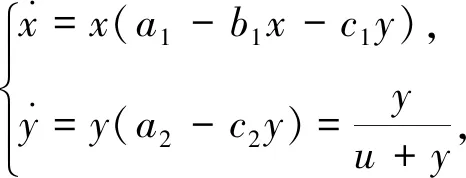
(4)

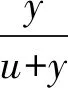
1 主要结论

引理1

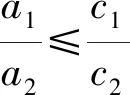
定理1系统(4)是持久的.

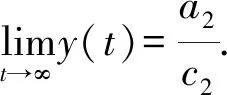
再由系统(4)的第一个方程

故有

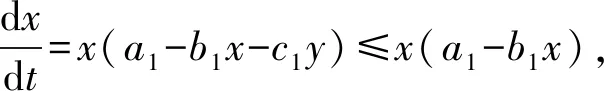
系统(4)对应的雅克比矩阵

J(x,y)=

故B(x*,y*)是局部渐近稳定的.

定理3系统(4)的正平衡点B(x*,y*)是全局稳定的.

证明由定理2可知正平衡点B(x*,y*)是局部渐近稳定的， 若系统(4)在G={x,y|x>0,y>0}内不存在极限环， 则该平衡点就是全局稳定的.

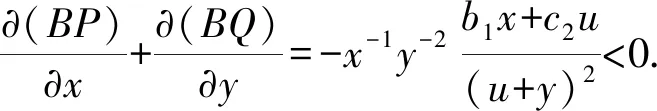
由文献[13]Dulac准则可知， 系统(4)在G={(x,y)|x>0,y>0}内不存在极限环， 所以正平衡点B(x*,y*)是全局稳定的， 证毕.

2 数值仿真

下面通过取一组满足系统(4)存在正平衡点情形的具体数据， 并通过Allee效应中u的改变来观察系统正平衡点稳定性变化的情况， 来验证Allee效应对系统正平衡点全局稳定的影响.取a1=2,a2=3,b1=0.5,c1=1,c2=4. 考虑系统

(5)

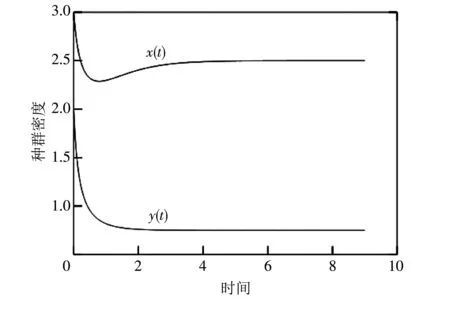
图 1 u=0.5的数值仿真图Fig.1 Numerical simulation when u=0.5

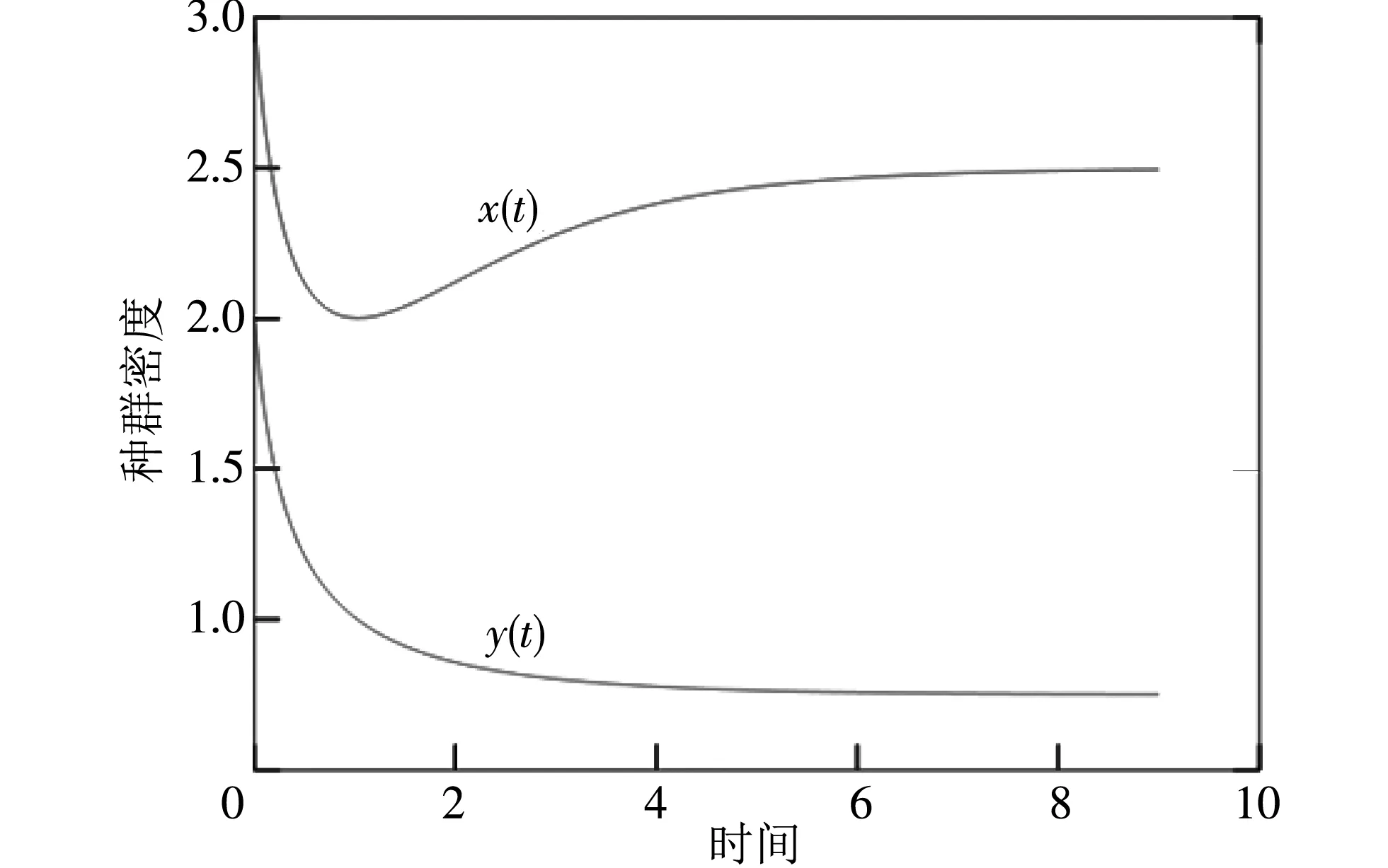
图 2 u=3的数值仿真图Fig.2 Numerical simulation when u=3

可以看出， 通过改变Allee效应常量的值， 发现系统的种群数量在一定时期内发生了改变， 但随着时间的推移， 最终都是趋于稳定的， 即Allee效应不会改变系统平衡点的全局稳定性.从这个意义上讲， Allee效应对系统具有不稳定的影响， 但这种影响是可控的.

3 结 论

本文通过对系统平衡点的分析发现， Allee效应中的参数并不影响系统平衡点的存在性. 同时， 在系统存在全局渐近稳定正平衡点的情形下， 对Allee效应中的参数u进行扰动， 数值仿真结果表明， 随着参数u的变化，系统达到稳定状态所需的时间是不同的， 对系统正平衡点的最终全局稳定性是没有影响的， 即Allee效应不影响种群的最终密度.