无线传感器网络可生存性评估研究

石 琼， 丁英华， 秦 丽， 宋礼鹏

(1. 中北大学 电子测试技术重点实验室， 山西 太原 030051；2. 中北大学 仪器与电子学院， 山西太原 030051； 3. 中北大学 大数据学院， 山西太原 030051)

0 引 言

WSNs是由众多传感器节点通过自组织的方式连接而成的无线网络. 近些年， 无线传感器网络快速发展， 已经广泛应用到各个领域当中， 甚至改变了人类生活与交流的方式. 由于WSNs的灵活性及便利性， 使其非常适合应用在环境恶劣或者敌对的区域， 但是， 在恶劣环境及敌对的战场环境下， WSNs极易受到恶意攻击， 发生故障或者意外事故. 这就要求WSNs不管是在恶劣环境之下， 还是在遭受恶意攻击时仍然能够提供服务， 这种能力就是可生存能力. WSNs可生存性评估就是对其生存能力的量化评估， 能够为增强WSNs的可生存性提供依据.

目前， 对于有线网络可生存性评估的研究已经有很多[1-2]， 但是针对WSNs的可生存性相关研究还相对较少. 由于WSNs能量、 存储及通信资源受限的特性， 有线网络中的可生存技术及可生存性量化评估方法不能完全应用到WSNs中， 因此， 必须根据WSNs自身的特点， 找到真正适合WSNs的可生存性评估方法.

本文针对受攻击的WSNs设计了WSNs生存性评估模型及评估量化指标， 利用连续时间马尔可夫链建立了生存性评估模型， 并对该模型进行稳态分析. 该模型描述了受攻击的传感器节点的四种状态以及状态之间的转换关系， 并实现了WSNs网络可生存性定量评估， 主要包括： 单个节点及整个网络的可靠度、 可用度、 可生存度的计算. 特别地， 本文将WSNs可靠性分为节点失效相互独立与相互关联两种情况来计算. 节点失效相互独立的情况下， 主要应用串并理论由单个节点的可靠性得到整个网络的可靠性； 节点失效相互关联的情况下， 结合串并理论与共因失效中的β因子模型求得整个网络的可靠性.

1 相关工作

可生存性的研究最早被提出是在军用通信网络中[3-4]， 目前已经广泛应用于传统网络中[5-6]， 但是对于网络可生存性的定义还没有统一的标准， 大部分研究者认可的是由CMU/SEI研究小组提出的定义： 指遭受攻击、 故障或意外事故的时候， 系统能够及时完成其关键服务的能力[7].

从网络安全的角度来看， 可生存性是网络安全领域一个新的研究方向[8-9]. 网络生存性的核心目标就是增强网络安全性， 提高网络可靠性. 入侵容忍是实现网络可生存性的主要技术之一， 旨在提高网络系统“容侵、 容灾、 容错”的能力.

目前， 大多数的研究对于网络可生存性只是定性的说明， 较少有研究者关注到可生存性的定量分析与评估问题. 其中， 一些研究者给出了可生存性的形式化描述， 文献[10]给出了可生存性定义的6元组形式化描述. 文献[11]提出了网络系统可生存性的8元组形式化描述， 并给出了其实现模型. 文献[12]不仅给出了生存性的形式化定义， 还与可靠性、 可用性等相关的概念进行了比较.

无线传感器网络由于其部署环境的特殊性， 更容易受到各种威胁， 同时传感器节点能量、 计算和存储能力受限， 使其检测威胁和从故障中恢复的能力有限， 故无线传感器网络的可生存性研究就更加重要. 无线传感器网络可生存性的评估指标也没有统一的标准， 是研究者根据具体的应用以及自己的理解来定义的. 文献[13]提出一种基于韧性的无线传感器网络生存性研究方法， 并利用基于模拟退火算法和粒子群优化算法的混合算法来计算网络节点的韧性. 文献[14]将生存性和可用性量化为： 可用性=1-故障状态概率； 可生存性=可用性-响应状态概率=1-故障状态概率-响应状态的概率.

目前较多的文献仅仅做了可靠性的分析评估. 文献[15]认为可靠性是评估移动无线传感器网络(MWSN)性能的重要指标， 并对MWSN可靠性理论进行了全面细致的研究. 文献[16-17]分析了影响WSNs可靠性的因素， 并描述了考虑WSNs故障评估和WSNs安全评估的可靠性评估过程.

WSNs的可生存性评估建模方法主要集中在基于网络结构、 基于网络状态和基于服务组件三种建模方式上. 其中， 基于网络状态的建模方式应用最为广泛， 特别是对于受到攻击的WSNs， 基于状态的建模方式非常适合刻画网络中各类节点的状态变化. 文献[14]和文献[18]分别利用连续时间马尔可夫链来描述无线传感器网络受到攻击时单个节点和单个簇的状态变化情况， 进而根据建立的生存模型， 对网络进行生存性评估.

本文应用连续时间马尔可夫链建立了受攻击的无线传感器网络的状态转换模型， 利用该模型对网络的可靠性、 可用性与可生存性进行了量化评估.

2 模 型

2.1 网络模型

2.1.1 网络拓扑结构

WSNs比较常见的拓扑结构主要分为两大类： 平面网络结构和层次网络结构. 平面网络结构中所有节点是对等的， 功能特性完全一致. 这种结构简单易维护， 比较适合规模相对较小的WSNs. 层次网络结构中的节点根据其承担的任务可分为骨干节点和一般节点. 层次网络结构通常以簇的形式存在， 每个簇由簇首节点(骨干节点)和成员节点(一般节点)组成， 整个网络可以由一个或多个簇组成. 簇首节点为上层节点， 采用平面型结构， 负责管理成员节点、 汇聚成员节点采集到的数据并转发、 为其他簇首节点转发数据等任务. 成员节点为下层节点， 负责采集数据发送给簇首节点， 其没有管理、 汇聚和中继的功能. 这种结构扩展性好， 便于管理， 网络可靠性高， 能有效延长网络生存期.

由于层次网络结构具有的优点非常适合本文中的评估模型， 故本文选择该网络结构作为研究可生存性评估方法的网络拓扑结构. 层次型WSNs工作过程： 簇内成员节点采集数据发送给所在簇的簇首节点， 簇首节点将收集到的数据发送给汇聚节点， 汇聚节点与传统网络(互联网、 卫星)相连， 最后将数据发送到传统网络中.

如图 1 所示， 层次型WSNs传输数据时的传输路由很明显表现出了串联与并联系统的特征. 具体地， 网络中每个簇可以看作是一个并联系统， 因为簇内任意一个成员节点发生故障都不会对其他节点造成影响， 即使是簇首节点发生故障， 也可以从簇内的候选簇首中选举出新的簇首节点代替故障簇首工作(事实上， WSN的很多协议中为了平衡负载， 都会遵循一定的原则来周期性地在簇内更换簇首节点)， 也就是说， 只有簇内所有节点都故障整个簇才会失效， 这正是并联系统的特征. 对于簇首层面的路由来说， 又可以看作是一个串联系统， 因为一条路由中只要有一个节点故障， 数据就无法成功到达汇聚节点， 这也正是串联系统的特性. 因此， 从源节点到汇聚节点的一条完整路由可以看作一个串并联系统. 而网络中不止一条路由(多路径路由)， 所以整个WSN可以看作一个并联系统， 数据能够通过不同的路由传输. 此外， WSN中通常会部署冗余节点来增强网络的可靠性， 这种方法也通常用于串并系统中来提高系统的可靠性. 综上， 采用层次型拓扑结构的WSN可以看作是一个复杂的串并联系统.

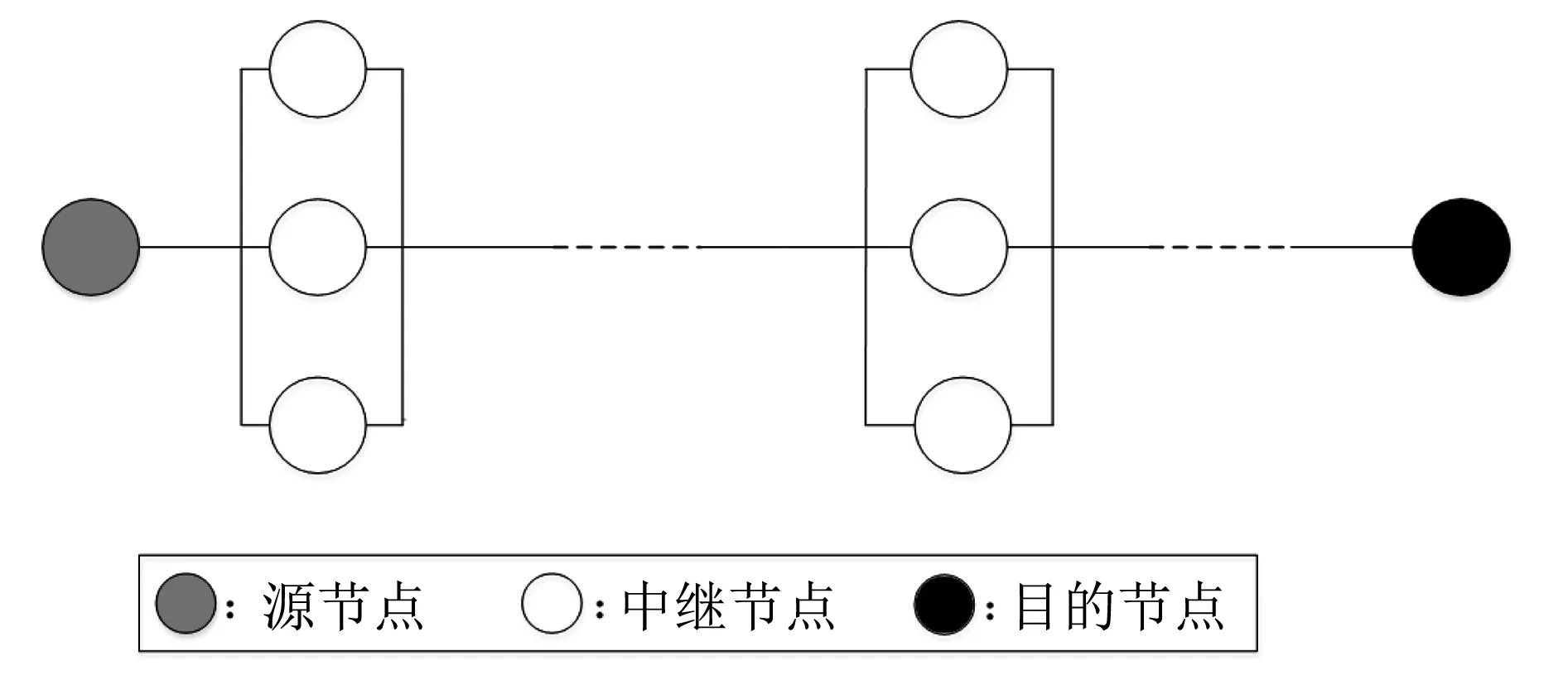
图 1 基于串并联系统的WSNs路由示意图Fig.1 Route in WSNs based on the serial-parallel system

2.1.2 网络假设

网络模型相关假设：

1) 传感器节点是易受攻击的. 而汇聚节点受到攻击时是健壮的， 这个假设在实际中通过相关的安全机制可以实现.

2) 传感器节点具有相同的初始能量.

3) 传感器节点在部署之后保持静止.

4) 网络中共有N个传感器节点，N=1,2,3,…,n.

5) 网络中共有M个簇，M≤N，M=1,2,3,…,n， 假设簇内节点数相同.

2.1.3 威胁模型

WSNs极易受到各种类型的攻击， 攻击分为外部攻击和内部攻击. 外部攻击是指在网络外部发起的攻击， 主要实现手段有监听、 捕获并克隆其它合法节点身份、 伪造、 篡改等. 内部攻击是指由网络内部被捕获的恶意节点发起的攻击， 主要实现手段有选择性转发、 捕获、 发布虚假路由信息等. 本文中考虑在网络中既存在外部攻击， 也存在内部攻击.

2.2 基于连续时间马尔可夫链的受恶意节点攻击的WSNs生存模型

本节将利用随机方法建立一个可生存模型， 通过传感器节点的状态转换过程来构建节点可生存模型. 受攻击的WSNs中， 因为攻击者发起攻击的时间是随机的， 所以触发传感器节点发生状态转换的时间是随机的， 那么受攻击的WSNs中节点的状态转换过程就可以通过连续时间马尔可夫链来表示.

2.2.1 状态转移模型

利用马尔可夫链建立传感器节点的状态转换模型， 该模型模拟遭受恶意攻击的传感器节点从一个状态向其它状态的转换过程(如图 2). 这里， 定义传感器节点的生命期包括四个状态： 健康(Healthy，H)、 妥协(Compromised，C)、 响应(Response，R)、 失效(Failure，F). 图 2 中H，C，R，F分别代表这四个状态；λij代表从状态i到状态j的转化速率.

假设节点以一定的概率处于某个状态下(节点在某个状态下是服从一定的概率分布的). 一个外部事件(例如： 攻击和防御)将触发节点从一个状态到下一个状态的运动. 传感器节点的状态转换过程： 节点的初始状态为H. 当节点遭受到恶意攻击之后将变为妥协节点， 它所处的状态从H转化为C. 如果入侵检测系统检测到节点已经遭受攻击并转化为状态C后， 节点马上进入状态R， 利用恢复机制(例如： 软件恢复、 重配置等方法)进行响应恢复. 否则， 节点继续留在状态C或由于受攻击后未采取响应动作而进入失效状态. 节点在状态R如果恢复成功则返回到状态H， 否则将继续留在状态R或进入到状态F. 此外， 传感器网络通常部署在敌对环境或者恶劣环境中， 可能会由于自然环境或者能量耗尽等原因造成节点的失效， 所以节点可能从状态H直接转化到状态F.

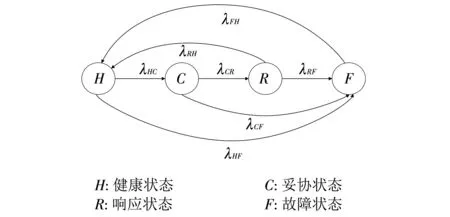
图 2 状态转移示意图Fig.2 State transition diagram

需要特别说明的是， 传感器节点一旦进入状态F就不可修复， 所以其不能从状态F转化到状态H， 但是在WSNs中通常会部署大量的冗余节点， 其作用一方面是为了提高数据的准确度和精度， 另一方面是为了延长传感器网络的生存期， 即节点进入失效状态， 冗余节点可能代替失效的节点继续工作， 所以， 在这里我们假设节点进入状态F后， 可以以一定的转化率从状态F转化为状态H， 但是并非所有失效节点都可以被替代， 也就是说并非所有处于失效状态的节点都可以转化到健康状态， 因此， 为了更贴近实际， 这个转化率在实验中设置得比较低.

2.2.2 稳态分析

传感器节点在其生命期中会以一定的概率处于状态H，C，R，F中的某一种状态中， 下面将分析传感器节点的稳态概率.

图 2 中， 传感器节点的状态集合S={H,C,R,F}, 假设π(t)={πH(t),πC(t),πR(t),πF(t)}， 其中πi(t)表示在t时刻传感器节点处于状态i的概率， 于是， 各状态处于稳态的概率可以表示为π={πH,πC,πR,πF}. 描述传感器节点各状态之间转换的状态方程可表示为

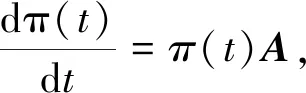
(1)

式中：A表示S中四个状态的状态转移矩阵， 矩阵中的元素aij,i,j∈S表示从状态i到状态j的转化速率， 表示为

于是可以得到状态转移矩阵

这里， 由平稳分布应满足的线性方程组和分布律性质可以建立平稳方程组， 过程如下

πA=0,

(4)

即

任选方程组(5)中的三个方程并与方程

πH+πC+πR+πF=1，

(6)

联立， 即可解得传感器节点的稳态概率

2.3 可生存性评估

2.3.1 可靠度

1) 单节点的可靠度

首先计算单个节点的平均无故障时间， 根据参考文献[19]中的方法， 通过前面给出的连续时间马尔可夫模型计算来得到.

计算平均无故障时间， 仅需关注工作和失效两种状态， 故可将状态集简化为S={SW,SF}. 其中，SW={H,C},SF={R,F}. 注意： 节点处于状态C时， 虽然表示已经遭到恶意攻击， 但是可以通过降低安全等级的方式来继续提供基本服务. 而在响应恢复状态R， 节点需要暂停服务， 所以将其归入失效状态.

状态转移矩阵A将被改为

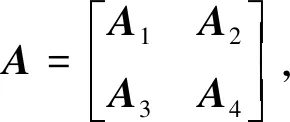
(8)

式中：A1,A2,A3,A4均为是2×2矩阵.A1中元素表示工作状态(H,C)之间的转化率；A2中元素表示工作状态向失效状态(R,F)的转化率；A3中元素表示故障状态向工作状态的转化率；A4中元素表示故障状态之间的转化率.

稳态概率也可按照工作与失效两种状态来表示， 即

π={πW,πF},

(9)

式中：πW={πH,πC},πF={πR,πF}.

假设给定t=0时刻的任一工作状态概率πW(0)， 且πH+πC=1.

为了便于计算， 假设状态R,F为吸收态， 即A3=A4=0， 那么状态方程可改写为

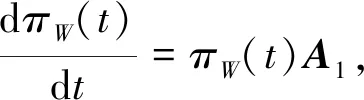
(10)

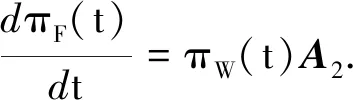
(11)

通过拉普拉斯变换， 可得如下方程(因为πF(0)=0)

(12)

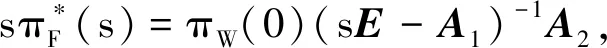
(13)

式中： “*”表示拉布拉斯变换；L{π(t)}≡π*(s).

系统在t时刻处于故障状态的概率为πF(t)h， 其中h是列向量. 因此， 失效概率密度的拉普拉斯变换为

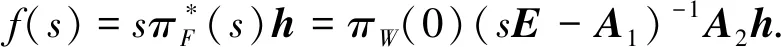
(14)

由于A中的行元素总和为0，

A2h=-A1h

(15)

且

f(s)=-πW(0)(sE-A1)-1A1h.

(16)

失效时间的r阶矩为

r!πW(0)(-A1)-rh.

(17)

通常使用1阶矩(均值)， 即

τ(1)=πW(0)(-A1)-1h.

(18)

通过选择适当的πW(0)可以确定失效时间的均值和矩.

在稳态概率已知的情况下，π={πWπF}， 系统在一个工作状态I的概率为πI/(πWh), 于是可得

πW(0)=πW/(πWh),

(19)

那么， 传感器节点的平均无故障时间MTTF可以计算如下

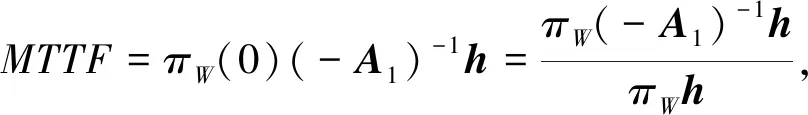
(20)

其中，

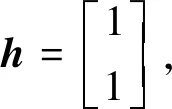
(21)

即

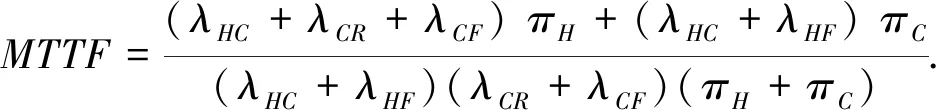
(22)

单个传感器节点的可靠度RSi(t)可以利用其失效率τ(t)计算，

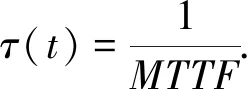
(23)

由失效率的性质[20]可得

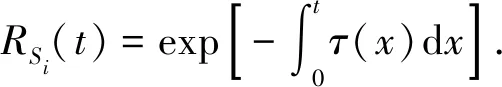
(24)

这里， 假设失效率为一个常量τ， 则

RSi(t)=exp(-τt).

(25)

2) 整个网络的可靠度

本文中将整个WSNs看作是一个复杂的系统， 将网络中的传感器节点看作是系统中的单元(组件). 要计算整个网络的可靠性， 可以先计算单个组件的可靠性， 再根据系统可靠性模型求出整个网络的可靠性.

文献[16]中在计算网络可靠性时使用的模型都要求网络中传感器节点的失效是相互独立的. 而在实际中传感器节点的失效并非都是相互独立的， 有些情况下它们的失效是相互关联、 相互影响的. 所以， 这里将分为两种情况讨论整个网络的可靠性.

a 节点仅存在独立失效

传感器节点仅存在独立失效的情况下， 可以通过系统可靠性模型中的串联系统和并联系统来计算网络的可靠度.

在层次型WSNs中， 簇中的任一节点失效都不会影响簇中其它节点的正常工作， 即使是簇首节点出现故障， 也可以通过重新选举簇首的方式来更换簇首节点， 只有簇内所有节点都失效整个簇才会失效. 这是典型的并联系统.

从源节点到sink节点要经过多个簇， 在此路由上只要有一个节点失效， 那么整条路由失效， 这是典型的串联系统.

从源节点到sink节点可能有多条路由， 只有所有路由均失效， 源节点到sink节点才无法连通， 这又可看作并联系统.

综合上述分析， 可以由单个节点的可靠度得到整个网络的可靠度.

假设每个传感器节点的失效率相同， 每个簇有相同的节点数m， 每条路由经过相同的簇数n， 从所有源节点到sink节点的总路由数为l.

如前所述， 一个簇可以看作并联系统， 即只有簇内所有节点都失效整个簇才会失效， 因此， 根据并联系统的可靠度公式[16,20]， 能够得到一个簇的可靠度为

1-(1-exp(-τt))m.

(26)

一条路由可以看作是一个串联系统， 即路由中只要有一个节点失效， 整条路由全部失效， 因此， 根据串联系统的可靠度公式[16,20]， 能够得到一条路由的可靠度为

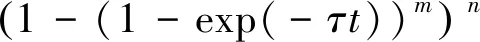
(27)

由于整个网络又可以看作是并联系统， 即网络中所有路由都失效则整个网络失效， 因此， 根据并联系统的可靠度公式[16，20]， 能够得到整个网络的可靠度为

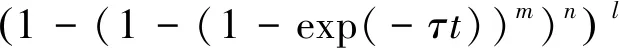
(28)

b 节点存在相关失效

在WSNs中， 各传感器节点失效并不是完全独立的， 可能存在相关失效. 本文主要讨论相关失效中的共因失效. 共因失效是指在某些共同原因的作用下， 造成了多个单元同时或者在一个时间间隔内失效. 两单元系统的独立失效和共因失效的关系如图 3 所示.

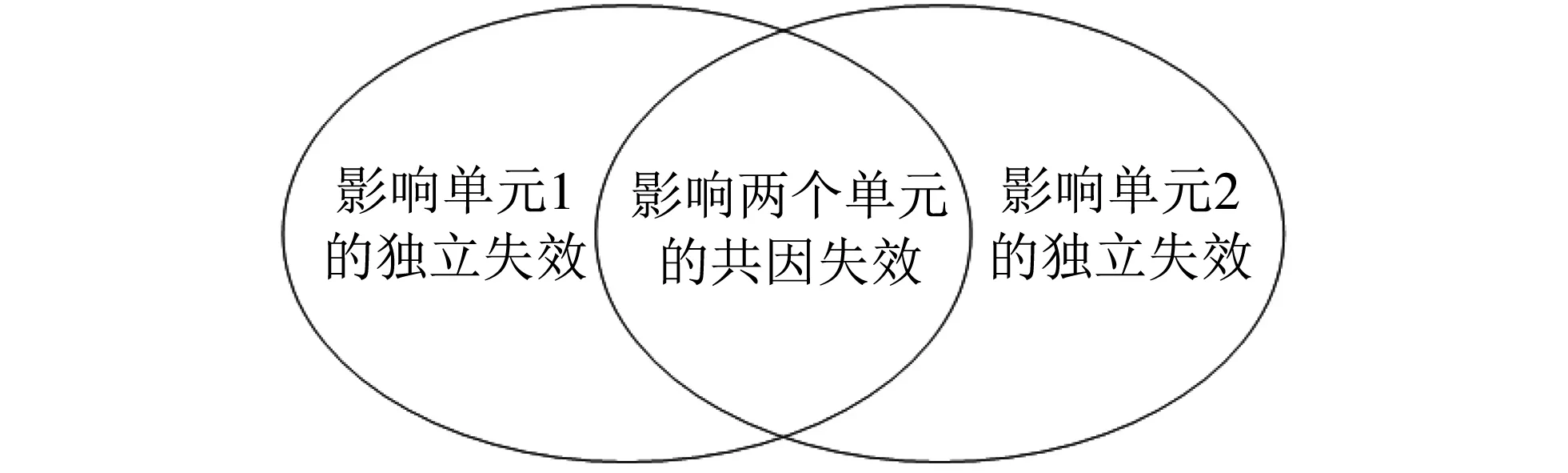
图 3 两单元系统的独立失效和共因失效的关系图Fig.3 Independent failure and common cause failure of two-unit system

假设引起节点失效的共同原因是内部恶意节点的攻击. 传感器节点由于遭受攻击这个共因(外部事件)引起的失效未必同时发生， 可能失效之间相隔很长时间， 但并不代表在失效的事件中没有联系.

这里， 利用相关失效模型的β因子模型来讨论传感器节点之间的相关失效[21].

β因子模型： 假设一个系统由k个相同单元组成， 每一个单元都有恒定的失效率τ. 且单元的失效由下面两个原因中的任一个原因造成：

1) 只与单元有关的环境.

2) 引起所有单元失效的外部事件.

设τ(i)表示由1)引起失效的失效率，τ(c)表示由2)引起失效的失效率. 这两个失效率相互独立， 则

τ=τ(i)+τ(c).

(29)

引入共因因子β，

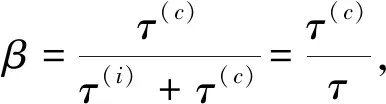
(30)

则

τ(c)=βτ,

(31)

τ(i)=(1-β)τ.

(32)

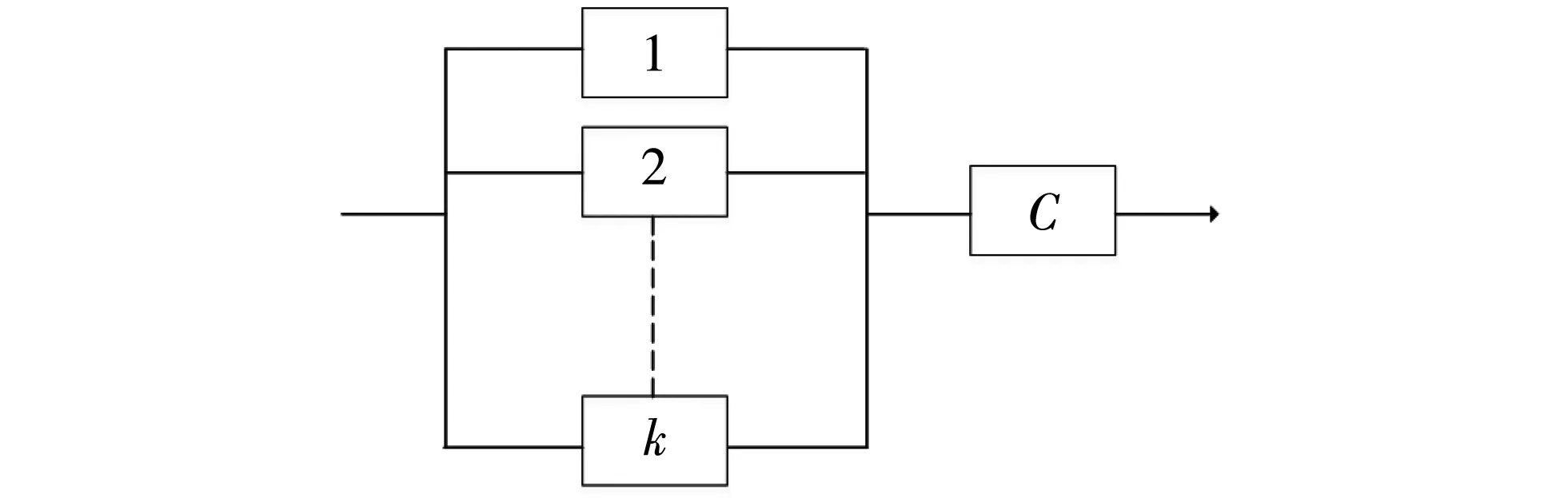
图 4 带有共因单元C的子系统结构Fig.4 Subsystem structure with common cause unit C

在受攻击的WSNs中， 传感器节点就相当于系统中的单元， 引起失效的原因2)中外部事件只考虑攻击者的恶意攻击. 因为层次型WSNs由一个或多个簇连接而成， 如前所述， 每个簇可以看作一个由k个相同传感器节点(单元)组成的并联系统， 其中每个传感器节点的失效率同样设为τ. 恶意攻击(外部事件)的发生可能引起并联结构中传感器节点的各自失效， 这个外部事件可以表示成单元C， 如图 4 所示， 单元C可以放入到系统其他部分的序列中. 单元C的失效率为τ(c)=βτ， 这里的单元C失效主要指被攻击捕获成为妥协节点. 并联系统中的k个节点相互独立， 失效率为：τ(i)=(1-β)τ， 则图 4 所示结构的可靠度可表示为

RSj(t)=(1-(1-Rsi(t))m)·RC(t)=

(1-(1-e-(1-β)τt)m)·e-βτt,

(33)

式中：Rsi(t)表示并联结构中一个传感器节点的可靠度，RC(t)表示传感器节点C的可靠度.

上面是网络中一个存在共因失效的簇(子系统)的可靠度， 下面我们推广到整个网络进行讨论. 假设任意一条路由可以看作是n个簇串联而成， 其中有w个存在共因失效的子系统， 其它子系统有n-w个， 从所有源节点到sink节点的总路由数为l. 为简化模型， 可以认为各子系统之间的失效是相互独立的， 且根据上一节的分析， 可得

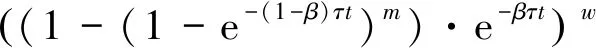
(1-(1-exp(-τt))m)(n-w),

(34)

1-(1-((1-(1-e-(1-β)τt)m)·e-βτt)w·

(1-(1-exp(-τt))m)(n-w))l.

(35)

式(34)表示一条路由的可靠度， 根据串联并联系统可靠度公式得到. 同理， 可以得到表示整个网络的可靠度计算公式(35).

2.4 可用度、 可生存度

可用性是指系统在执行任务的任意时刻能正常工作的概率. 可靠性是在给定的时间间隔内(和给定条件下)系统能正确执行其功能的概率. 可用性不仅与系统失效概率有关， 而且与系统的修复概率相关.

可用性的概率度量称为可用度， 这个参数是把维修性、 可靠性与保障性结合在一起考虑的综合性指标. 由于本文利用连续时间马尔可夫链建立WSNs的生存模型， 故考虑网络的稳态可用度作为一个网络性能评价指标. 稳态可用度是指当时间趋于无穷大时， 瞬时可用度函数的极限值. 稳态可用度可以通过连续时间马尔可夫链的稳定点得到.

可生存性是指在遭受攻击或意外事件时， 即使关键部分遭到破坏， 系统仍然能够及时完成其关键任务和提供服务的能力. 可生存性的概率度量称为可生存度.

1) 单节点可用度、 可生存度

在传统的可靠性评估中， 只考虑设备的两种状态， 即： 正常工作状态、 失效(故障)状态. 本文中考虑在网络受攻击的情况下， 传感器节点可能处于的四种状态， 即健康、 妥协、 响应(恢复)、 失效. 健康状态和妥协状态如2.3.1中所述都属于正常工作状态.

在响应状态下， 系统基于软件恢复和重配置等对抗攻击的手段(例如重启、 复位等)对妥协节点进行响应恢复， 响应成功后节点转换到健康状态， 响应失败后转换到失效状态. 所以在响应状态节点并非完全失效， 这里定义节点在响应状态也是可用的[14]. 故其稳态可用度可表示为

Ai=πH+πC+πR.

(36)

生存性强调的是任务和服务， 提供预定义的最小级别服务的能力， 故即使在妥协状态， 我们仍然认为节点是可生存的. 节点的可生存度可表示为

Si=πH+πC.

(37)

2) 整个网络的可用度、 可生存度

由于WSNs的特殊性， 网络中会部署较多冗余节点， 故网络的容错容侵能力较强. 单个节点或少部分节点的生存能力不能代表整个网络的生存能力， 需要综合考虑网络中大部分节点的生存情况. 因此， 这里定义网络中有50%以上节点是可生存的， 那么整个网络就是可生存的. 也就是说， 整个网络能够提供正常服务的概率由50%以上节点的生存概率决定， 则整个网络生存度可定义为[22]

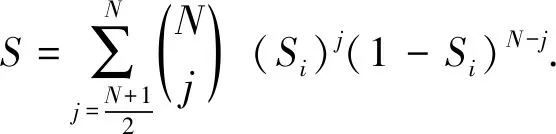
(38)

类似地， 可以定义整个网络的可用度为

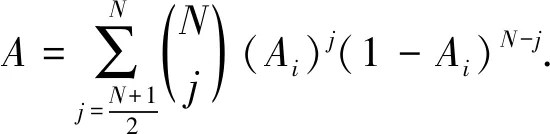
(39)

3 模型仿真

3.1 仿真参数设置

参考相关文献并根据实际情况， 本文中的参数设置如表 1 所示.

表 1 参数表

3.2 仿真实验设置

根据2.3与2.4节中描述的生存性评价指标， 使用MATLAB R2018b对本文提出的模型进行仿真实验， 共进行了5组仿真实验.

仿真实验1： 节点的平均无故障时间MTTF. 本实验考查两个参数λHC，λCR的取值变化对节点的平均无故障时间MTTF的影响. 分别将λHC或λCR设为在[0,1]区间变化的值， 考查MTTF的变化情况.

仿真实验2： WSNs可靠度量化实验(仅存在独立失效). 本实验考查在仅存在独立失效的情况下， 簇内节点数、 路径中经过节点数以及总路径数的变化对整个网络的可靠度的影响.

仿真实验3： 存在共因失效的子系统及网络可靠度量化实验. 本实验考查存在相关失效的情况下， 共因因子的变化对子系统以及整个网络可靠度的影响； 存在共因失效的子系统在整个网络中的数量对网络可靠度的影响； 簇内节点数、 路径中经过节点数以及总路径数的变化对整个网络的可靠度的影响.

仿真实验4： WSNs可用性量化实验. 本实验考查转化率λHC，λCR，λRH的变化对整个网络的可用度的影响. 实验中， 将三个转化率中的任意两个值固定， 第三个值在[0,1]区间变化， 考查网络可用度的变化情况.

仿真实验5： WSNs可生存性量化实验. 本实验考查转化率λHC，λCR，λRH的变化对整个网络的可生存度的影响. 实验中， 将三个转化率中的任意两个值固定， 第三个值在[0,1]区间变化， 考查网络可生存度的变化情况.

3.3 实验结果及分析

3.3.1 节点的平均无故障时间MTTF

图 5 表示λHC，λCR的取值变化对平均无故障时间MTTF的影响. 图 5 中，x轴、y轴、z轴分别表示λHC，λCR，MTTF. 从图中可以看出， 随着λHC或λCR取值的增大，MTTF的值迅速减小.

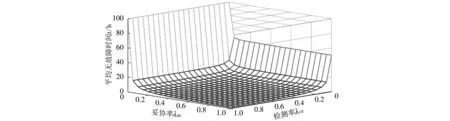
图 5 妥协率λHC、 检测率λCR对节点平均无故障时间MTTF的影响Fig.5 Impact of compromise probability λHC and detection probability λCR on MTTF of nodes

1) 当状态C向状态R的转化率(即检测率)固定取值时， 考虑两种情况： 第一种情况， 响应率λCR=0.1， 状态H向状态C的转化率λHC从0变化到1，λHC=0时，MTTF=100；λHC=0.1 时，MTTF迅速降至12.88，λHC=0.3时，MTTF=9.178，λHC取值在0.5之后，MTTF的值仅从 8.681下降至8.431， 下降缓慢. 总降幅91.56%. 第二种情况， 响应率λCR=0.8， 状态H向状态C的转化率λHC从0变化到1,λHC=0时，MTTF=100，λHC=0.1时，MTTF迅速降至9.223，λHC=0.3时，MTTF=3.552，λHC取值在0.7之后，MTTF的值仅从1.97下降至1.66， 下降缓慢. 总降幅达到98.34%. 实验结果显示， 两种情况下，MTTF降幅接近， 但与第一种情况相比较， 第二种情况响应率高， 转化到响应状态的转化率较高， 响应状态是非工作状态， 所以第二种情况下的MTTF值较低.

2) 当状态H向状态C的转化率固定时， 考虑两种情况： 第一种情况， 当节点(网络)被攻击程度较轻时， 妥协率λHC=0.1， 状态C向状态R的转化率λCR从0变化到1，λCR=0时，MTTF=50.76；λCR=0.1时，MTTF=12.88， 降幅明显； 而λCR从0.3增加至1，MTTF从9.835缓慢降至9.178. 总降幅81.9%. 由实验结果可以看出， 与λHC的取值变化相比较，λCR的变化对MTTF的影响较小， 特别是λCR的取值大于0.3之后，MTTF的值仅下降0.657， 降幅仅6.7%. 在这种情况下， 可以认为， 防御比检测更加重要. 第二种情况， 当节点被攻击程度较严重时，λHC=0.8，λCR=0时，MTTF=50.02，λCR=0.5时，MTTF=2.397，λCR=1时，MTTF=1.666， 总降幅96.67%. 实验结果显示， 当攻击程度较严重时， 检测率的变化对MTTF的影响也较大. 因为此时转化到妥协状态的转化率较大， 检测率越大， 节点转化到响应恢复状态的转化率越大， 那么MTTF就会越低. 而在第一种情况中， 节点转化到妥协状态的转化率较小， 即使检测率再高也不会对MTTF有很大影响， 检测率提高到一定程度之后对MTTF的影响就变得很小.

表 2 检测率λCR 、 妥协率λHC对MTTF的影响

从表 2 中可以看出， 在其他参数相同的情况下， 妥协率的变化对MTTF的影响比检测率略高， 也就是说相比之下， 防御的重要性更高. 当然， 在条件允许的情况下， 防御和检测都做好是最理想的情况.

3.3.2 WSNs可靠度(存在独立失效)

图 6(a) 显示了不同簇内节点数量对整个网络的可靠度的影响. 图 6(a) 中三条线分别代表簇内节点数m=5， 10， 15(n=5，l=5)时， 网络可靠度随时间变化的曲线. 从图中可以看出，m的值越大， 网络可靠度越高， 也就是说， 一个簇内节点数越多， 网络的可靠度越高， 这符合一个并联系统的特性. 图 6(b) 显示了路径中经过的节点数对整个网络的可靠度的影响. 图 6(b) 中四条线分别代表一条路径中经过的节点数n=5， 10， 15， 20(m=5，l=5)时， 网络可靠度随时间变化的曲线. 如图中所示，n的值越大， 网络可靠度越低. 这说明一条路径中经过的节点数越少， 网络越可靠， 符合串联系统的特性. 图 6(c) 显示了网络中路径的数量对整个网络的可靠度的影响. 图 6(c) 中四条线分别代表网络中路径的数量l=5， 10， 15， 20(m=5，n=5)时， 网络可靠度随时间变化的曲线. 如图， 网络中路径数越多， 网络可靠性越高， 这就表明可以通过增加可用路由数来提高WSNs的可靠性.

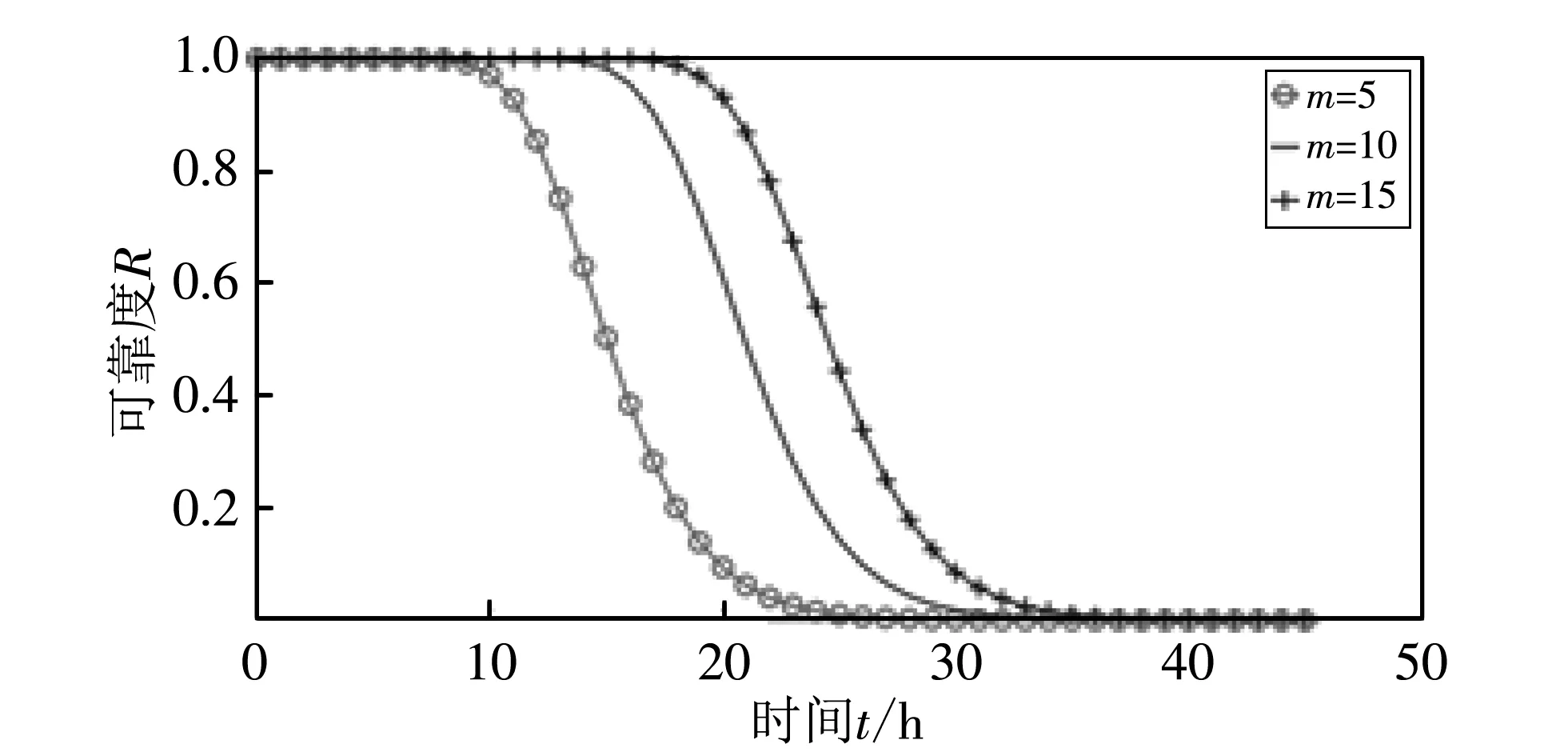
(a) m变化(λHC=0.1， λCR=0.8)

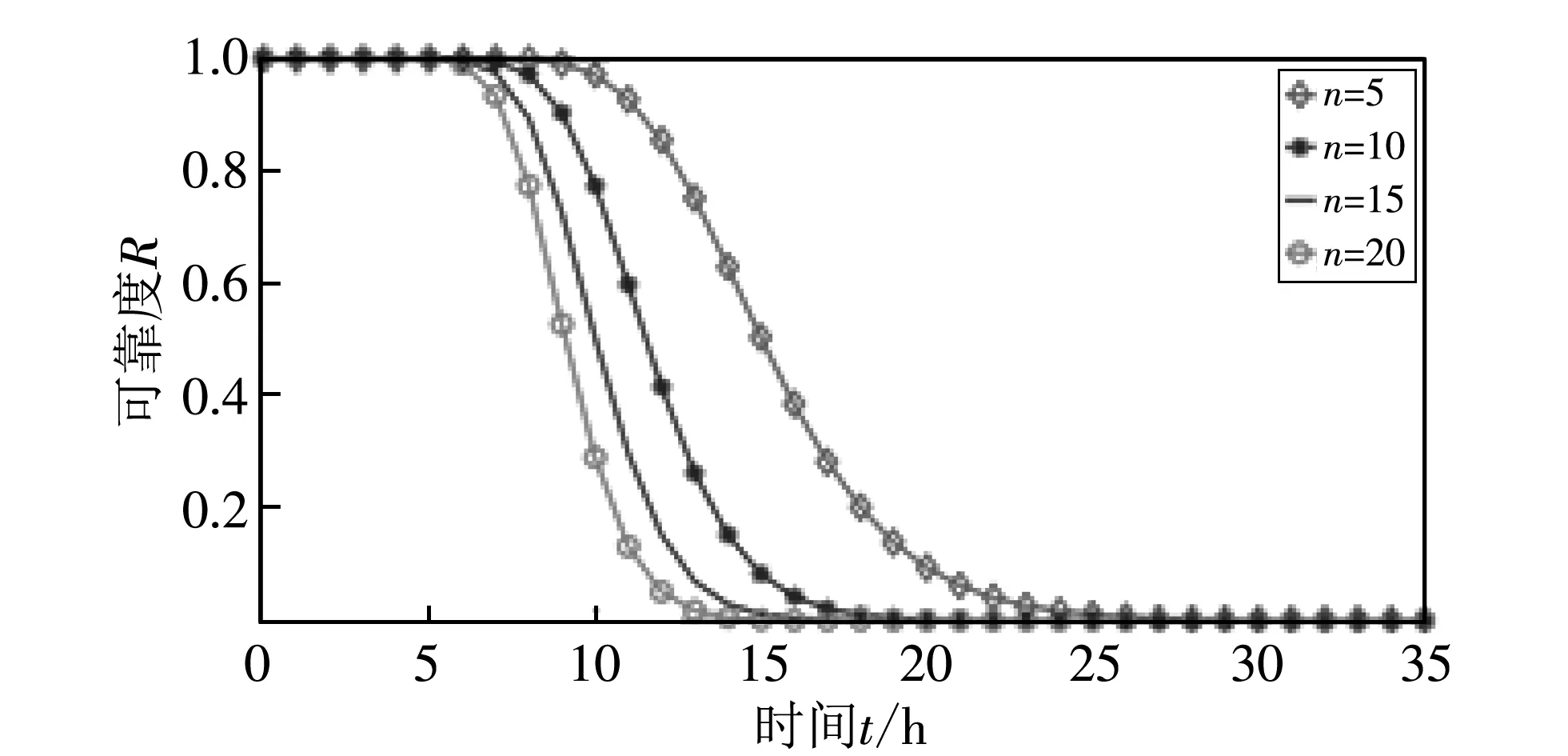
(b) n变化

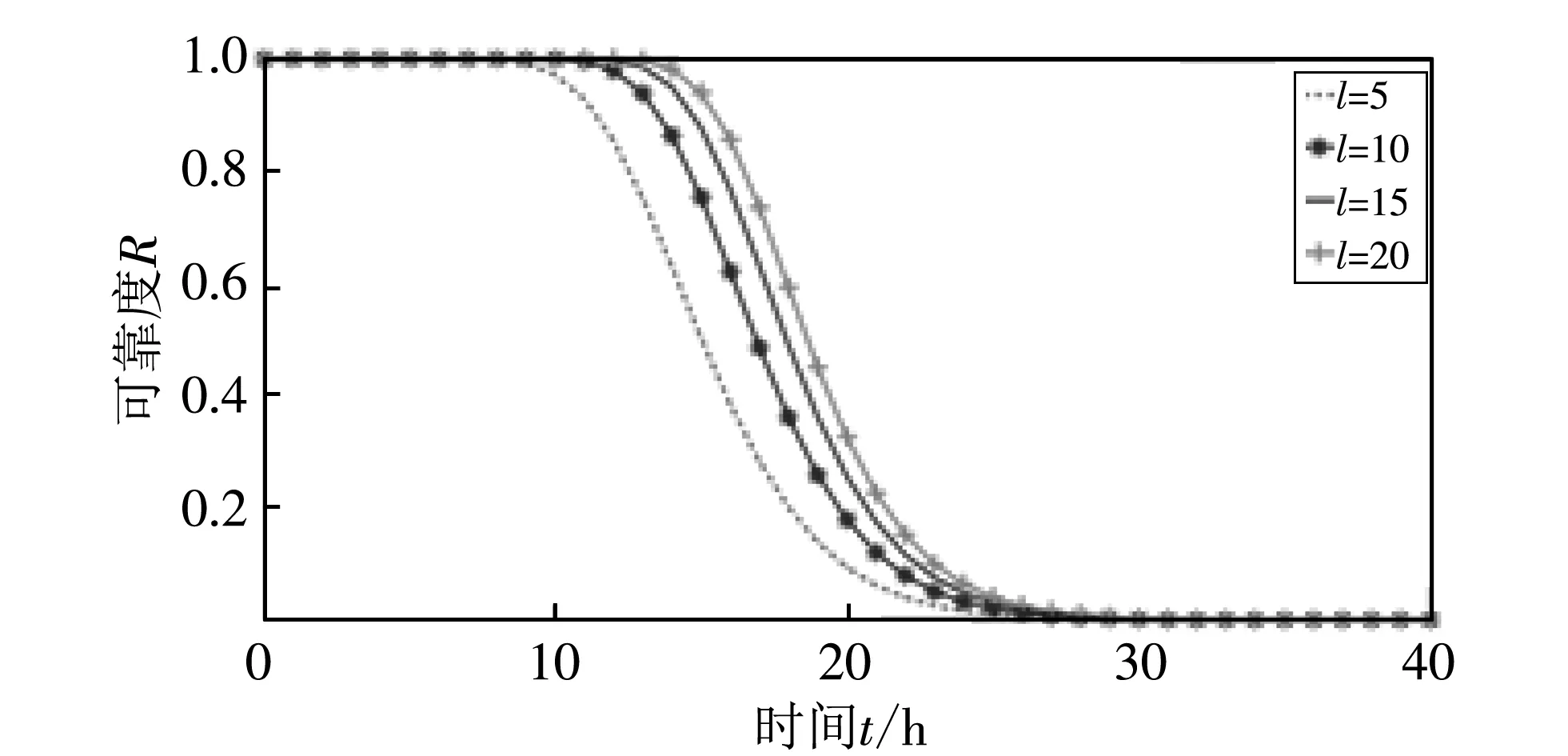
(c) l变化

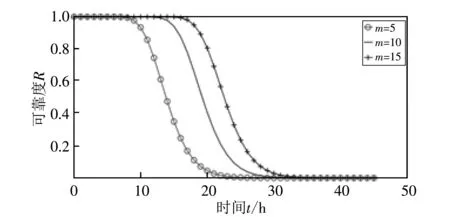
(d) m变化(λCR=0.1， λHC=0.8)

图 6(a) 中显示的是妥协率λHC=0.1， 检测率λCR=0.8时的实验结果， 图 6(d) 显示了λCR=0.1，λHC=0.8时， 簇内节点数m=5， 10， 15(n=5，l=5)时， 网络可靠度随时间变化的曲线. 对比图 6(a) 与图 6(d) 可知， 妥协率λHC=0.1， 检测率λCR=0.8时， m=5时可靠度降至0.5要经过15 h，m=10时可靠度降至0.5要经过20 h，m=15时可靠度降至0.5要经过24.5 h； 而妥协率λHC=0.8， 检测率λCR=0.1时，m=5时可靠度降至0.5要经过13.83 h，m=10时可靠度降至0.5要经过19.25 h，m=15时可靠度降至0.5要经过 22.4 h. 由实验结果可以看出， 妥协率高、 检测率低的情况下， 网络可靠度下降更快， 也就是说， 妥协率对网络可靠度的影响略大， 与检测相比较， 防御更加重要， 此结论与实验3.3.1中的结论一致， 并且也符合实际. 此外，n、l取不同值时的结果与上述结果一致， 这里不再赘述.

3.3.3 存在共因失效的子系统及网络可靠度

图 7 显示了共因因子的变化对子系统的可靠性的影响. 图 7 中三条线分别代表共因因子β为0.1， 0.5， 0.8时， 子系统(m=5)可靠度随时间的变化情况. 由图看出， 共因因子越大， 也就是共因失效所占比例越大(独立失效所占比例越小)， 子系统的可靠性下降得越快、 可靠性越低.

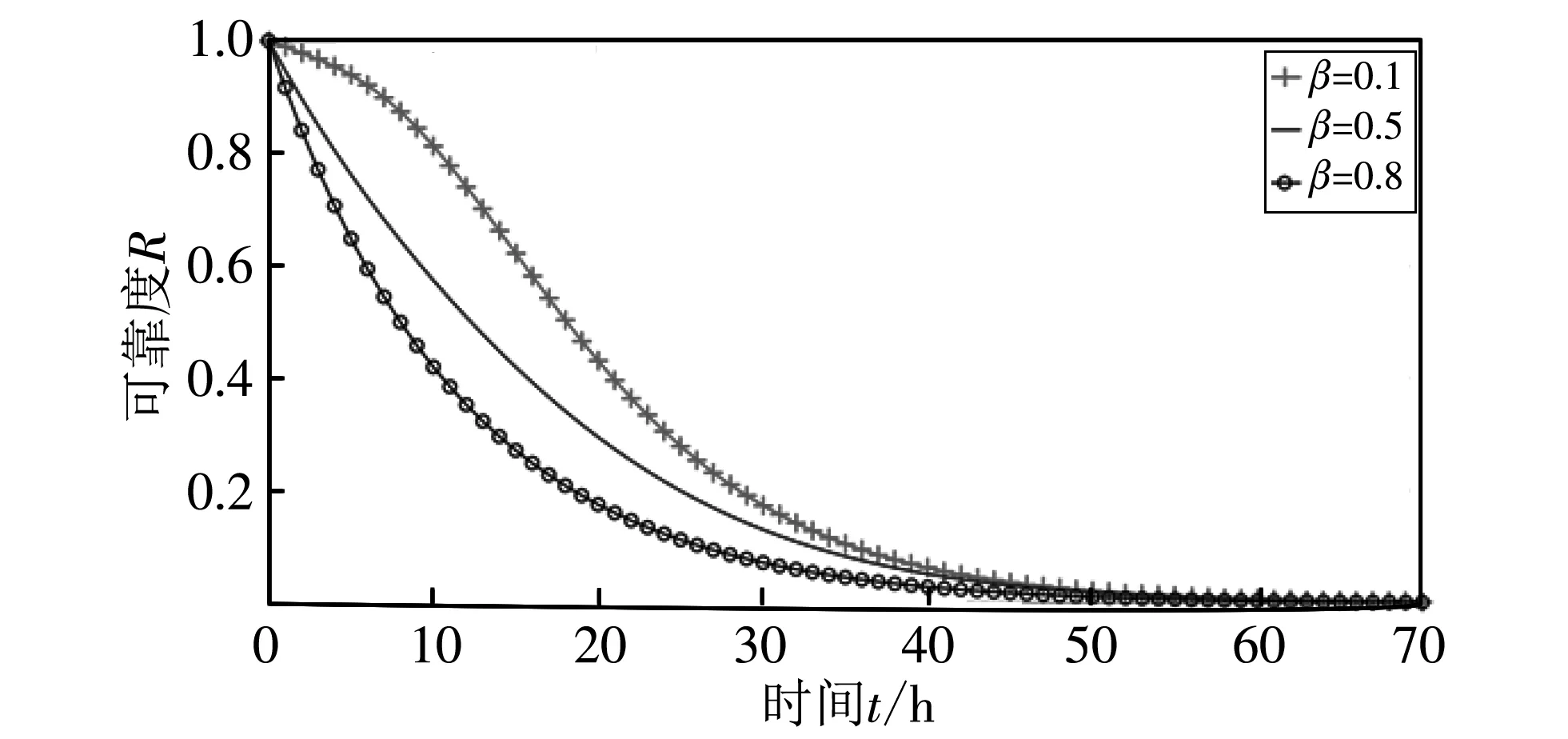
图 7 共因因子β对子系统可靠度的影响Fig.7 Impact of common cause factor β on the reliability of the subsystem

图 8 显示了共因因子的变化对整个网络的可靠度的影响.

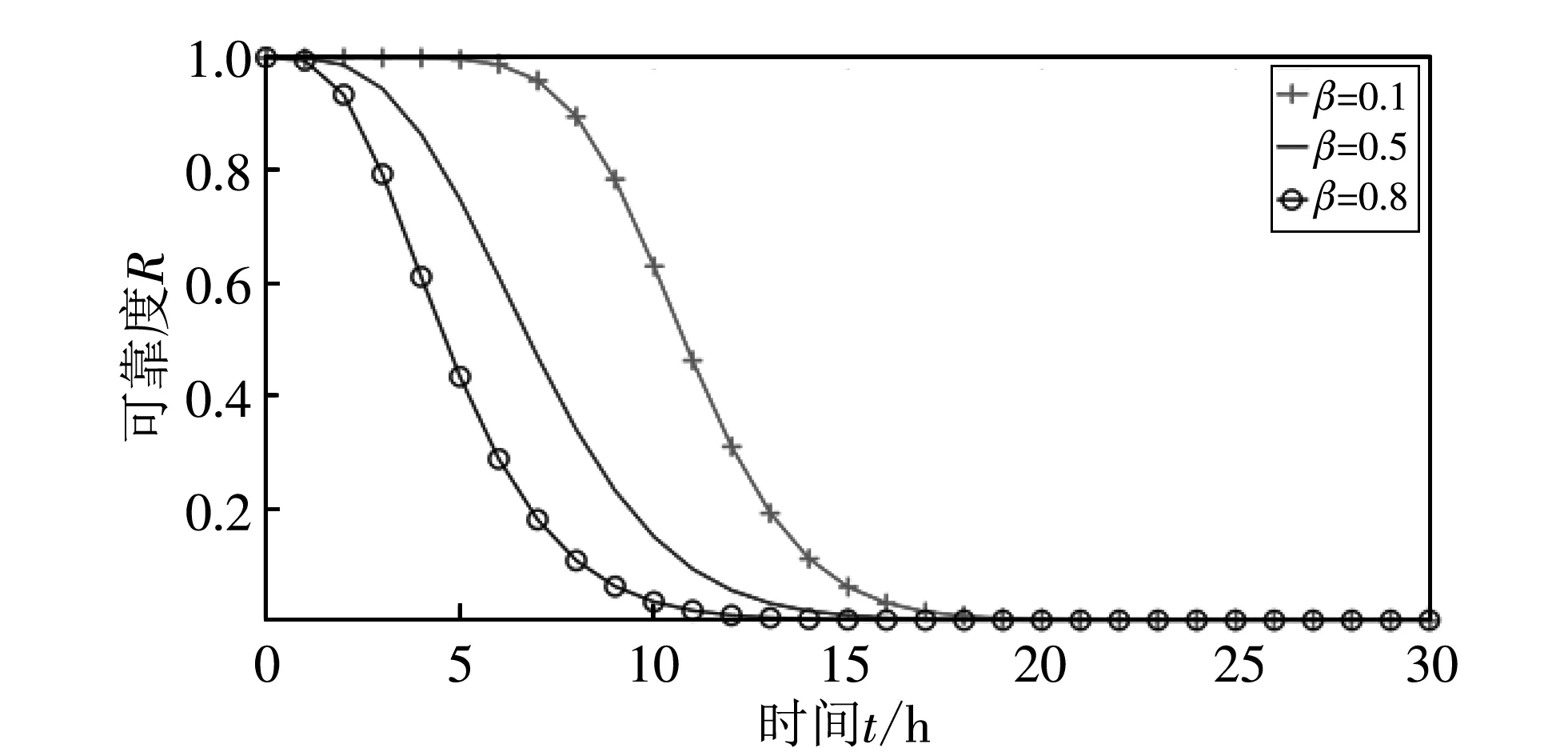
图 8 共因因子β对整个网络可靠度的影响Fig.8 Impact of common cause factor β on the reliability of WSNs

前面已经提到假设任意一条路由可以看作是n个簇串联而成， 其中有w个存在共因失效的子系统， 其它子系统有n-w个， 整个网络共有l条路由. 此时， 取n=10，w=5，m=5，l=5. 图 8 中三条线分别代表共因因子β为0.1， 0.5， 0.8时， 整个网络的可靠度随时间变化的情况. 随着共因因子β的增大， 整个网络的可靠度降低.

实验结果说明， 共因失效与独立失效相比， 对可靠性的影响更大. 在本模型中， 共因失效主要考虑受到内部恶意节点攻击的情况， 独立失效主要考虑节点遭到外部攻击的情况. 那么可以看出， 受到恶意攻击会更迅速地降低可靠性， 且内部攻击比外部攻击危害更大.

图 9 显示了存在共因失效的子系统在整个网络中的数量对网络可靠度的影响. 此时取n=10，l=5，m=5，w=1， 5， 9，β=0.5. 如图所示， 存在共因失效的子系统数量越大， 整个网络可靠度越低. 实验结果表明， 与独立失效相比， 共因失效对网络可靠性的影响更大， 这与前面的结论一致.

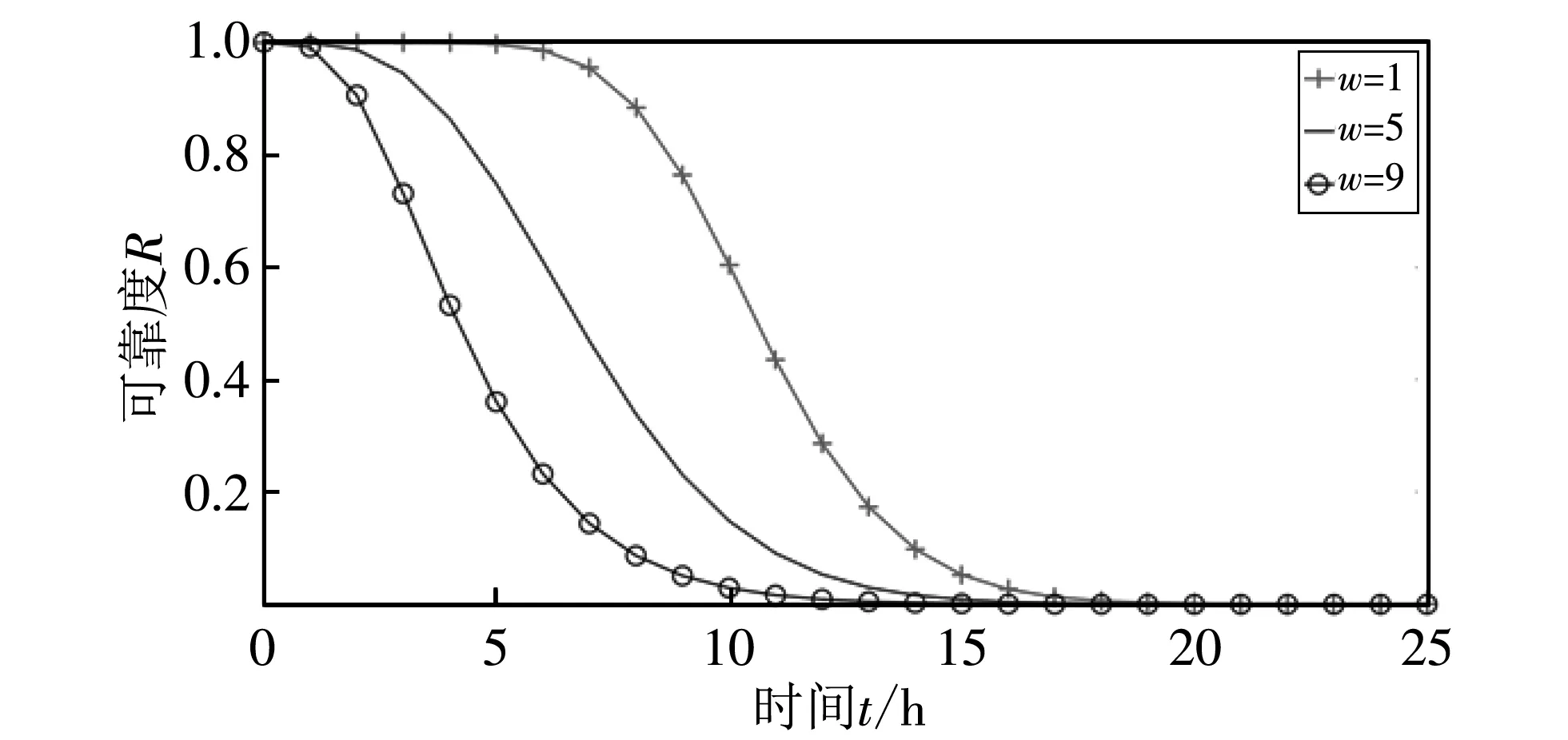
图 9 子系统数量对网络可靠度的影响Fig.9 Impact of the number of subsystems on the reliability of WSNs

图 10 代表在共因失效存在的情况下， 簇内节点数、 路径中经过的节点数和路径数变化时， 整个网络可靠度的变化曲线. 实验结果与图 6 一致， 簇内节点数或路径数越多， 网络可靠性越高； 而路径中经过的节点数越多， 网络可靠性越低. 这些结论为设计高可靠性的WSNs提供了依据.

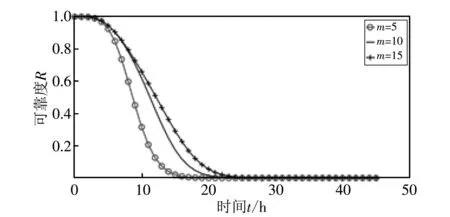
(a) m变化(w=3， n=10)

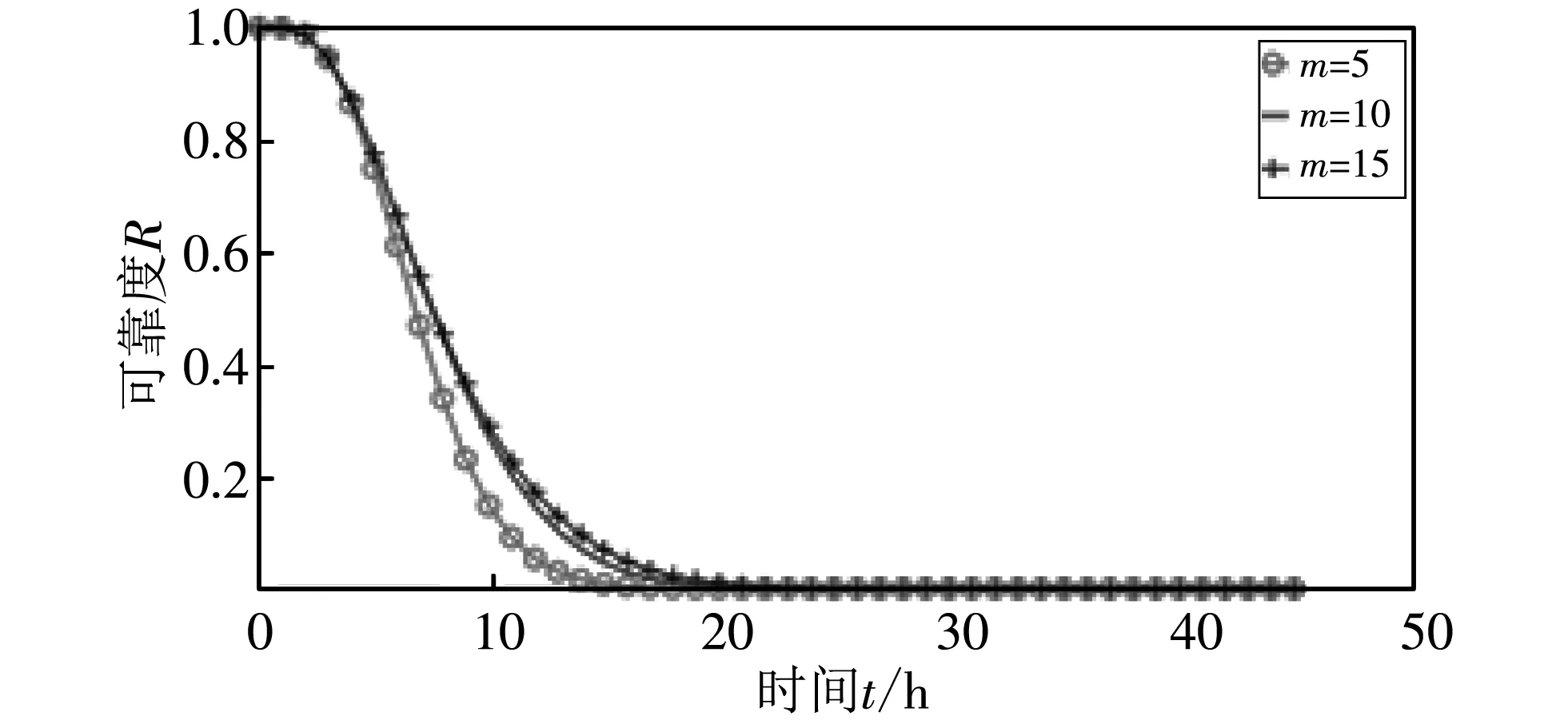
(b) m变化(w=5， n=10)

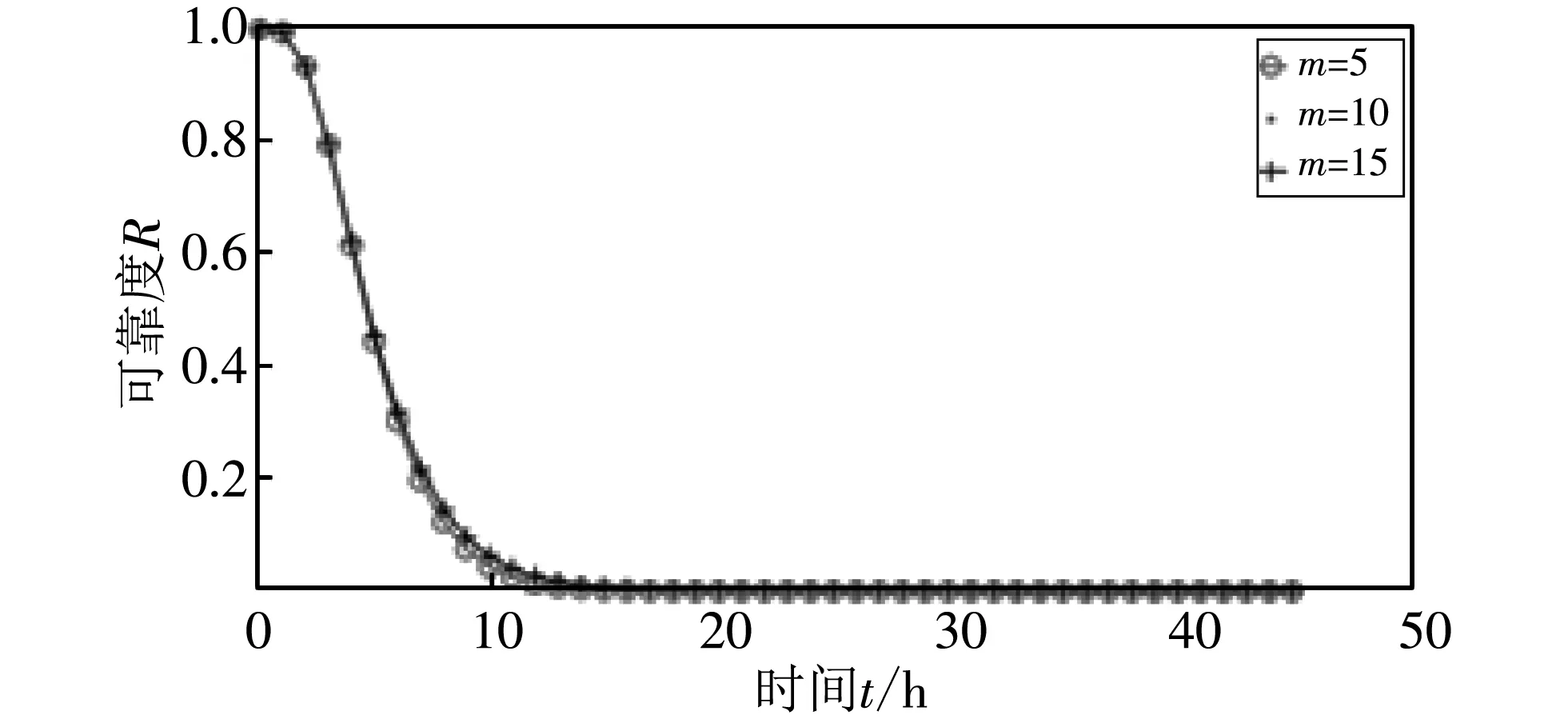
(c) m变化(w=8， n=10)

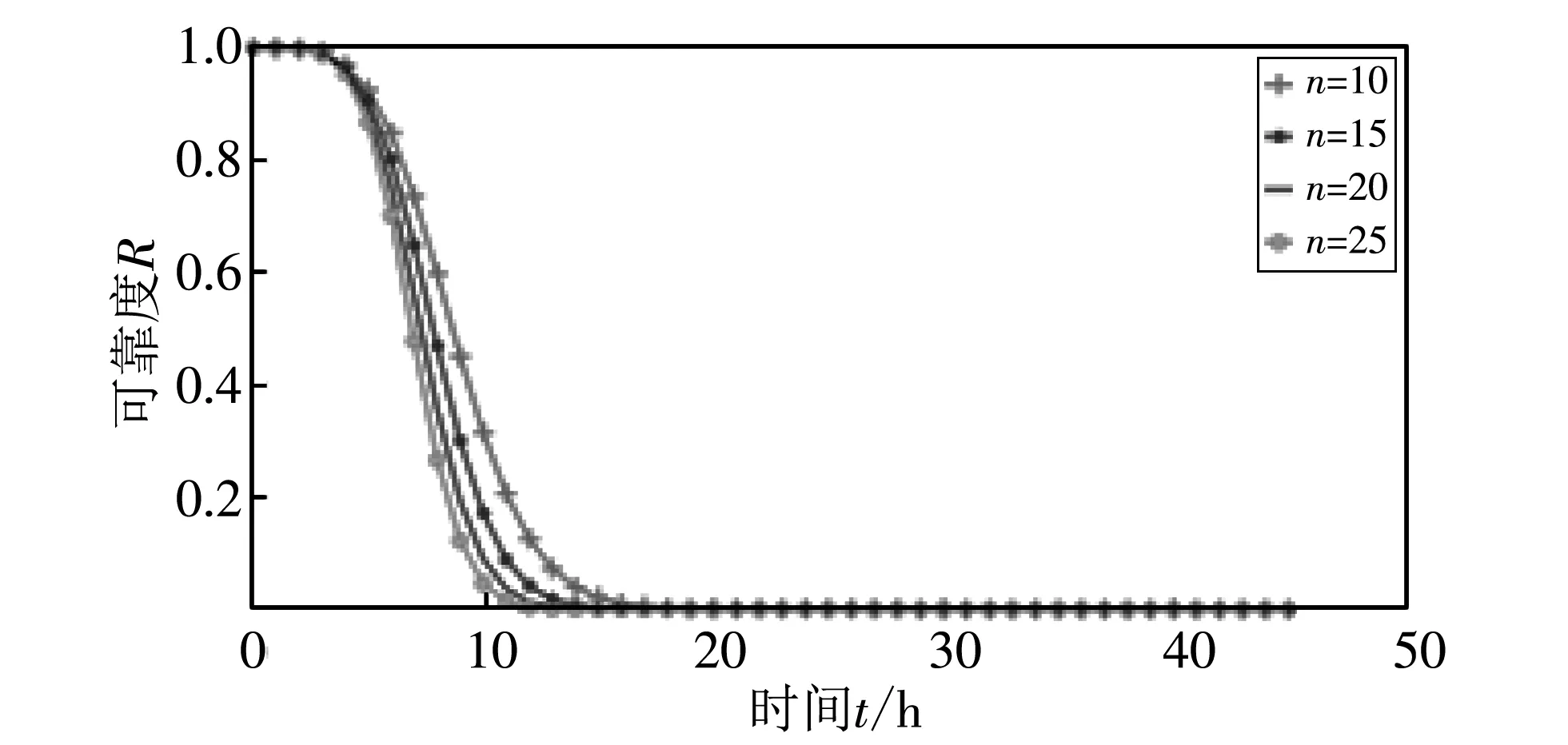
(d) n变化(w=3， n=10)

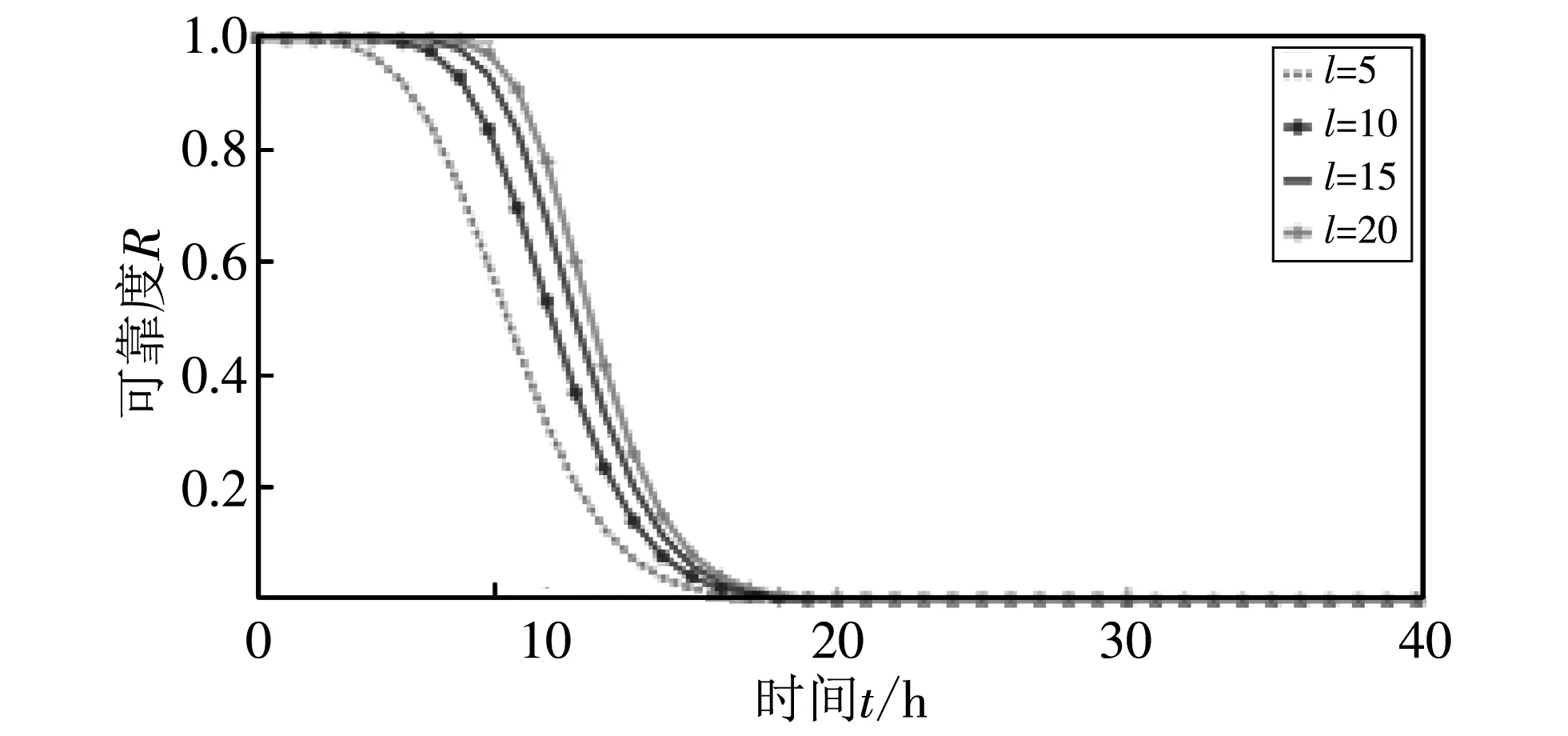
(e) l变化(w=3， n=10)

(f) l变化(w=5， n=10)

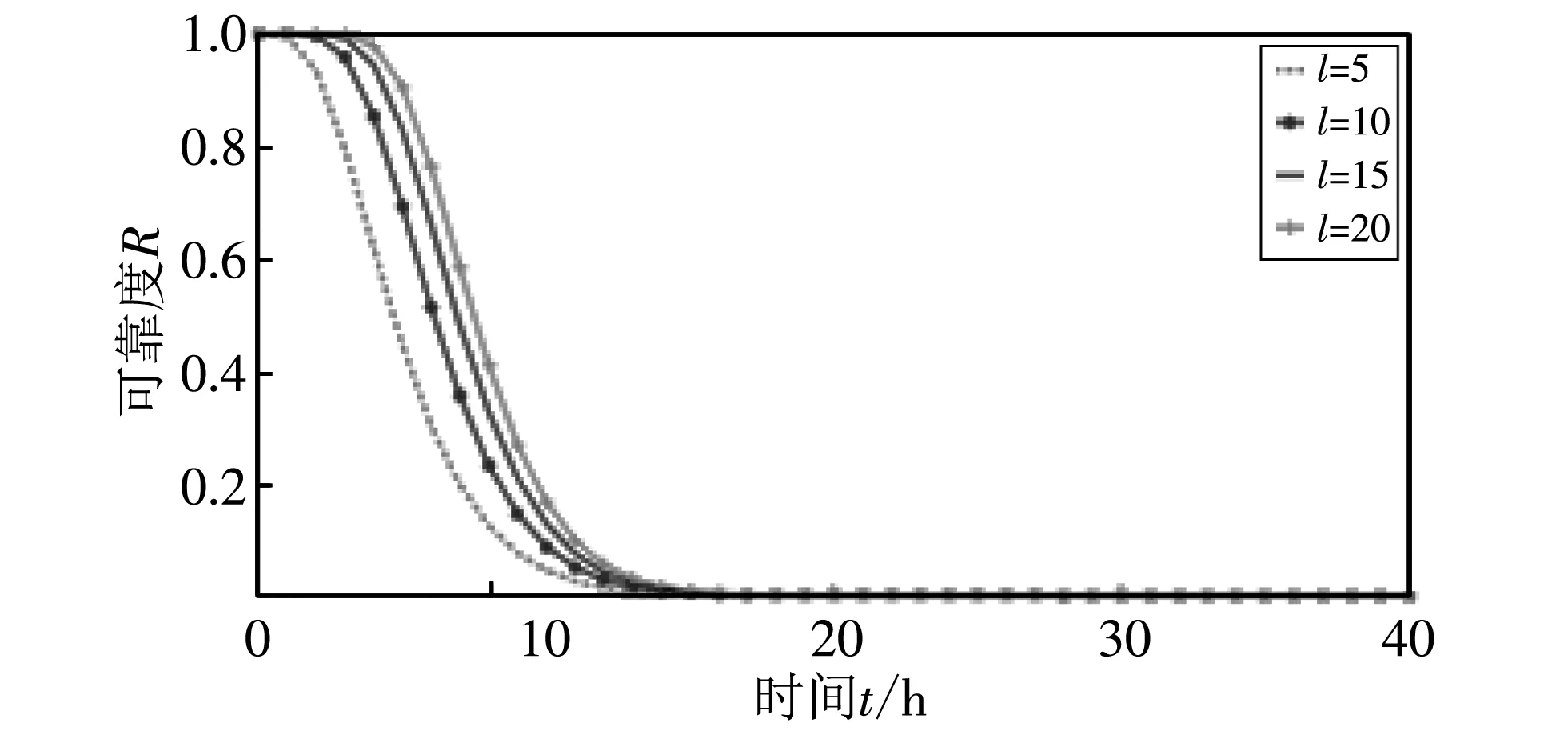
(g) l变化(w=8， n=10)

图10(a)～图10(c) 三个图代表w的取值逐渐增加(w=3,5,8，n=10，l=5，β=0.5)， 簇内节点数m分别为5,10,15时， 网络可靠度的变化曲线. 由图可以看出，w的值越大， 三条曲线越接近， 最后几乎重合. 这是因为带有共因失效的子系统中节点都受到同一个外部事件的影响导致其失效， 所以节点数量对网络可靠度的影响很小， 也就是说存在共因失效的情况下， 路径中经过带有共因失效的子系统越多， 簇内节点数m的大小对网络可靠度的影响越小.

图10(e)～图 10(g) 三个图代表w的取值逐渐增加(w=3,5,8，n=10，m=5，β=0.5)， 路径数l分别为5,10,15,20时， 网络可靠度的变化曲线. 与图 10(a)～图 10(c) 不同，w的值增加只是使得整体的网络可靠度都降低， 但是仍然能看出l的取值越大网络可靠度越高. 因此， 可以得出结论， 考虑共因失效存在的情况下(特别是共因失效发生比例较大时)， 要提高网络整体的可靠度， 增加网络中可用路径数比增加簇内节点数更有效.

3.3.4 WSNs可用度

图 11 显示了转化率λCR,λHC,λRH逐渐增加的情况下， 整个网络的可用度变化曲线.

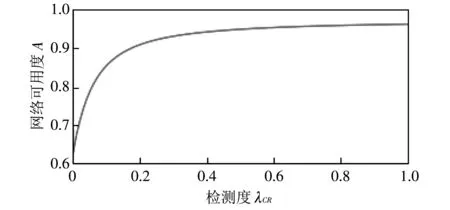
(a) 检测率λCR从0变化到1

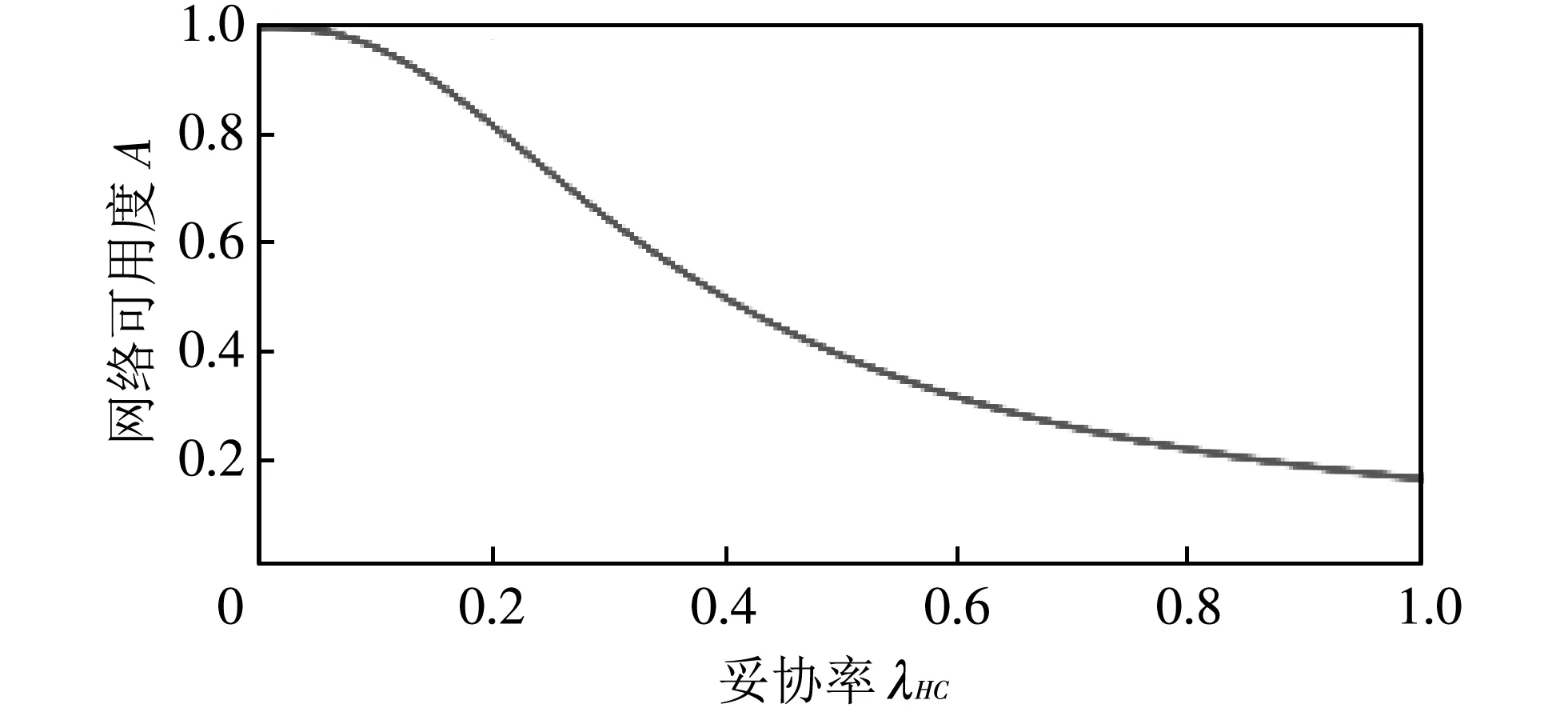
(b) 妥协率λHC从0变化到1

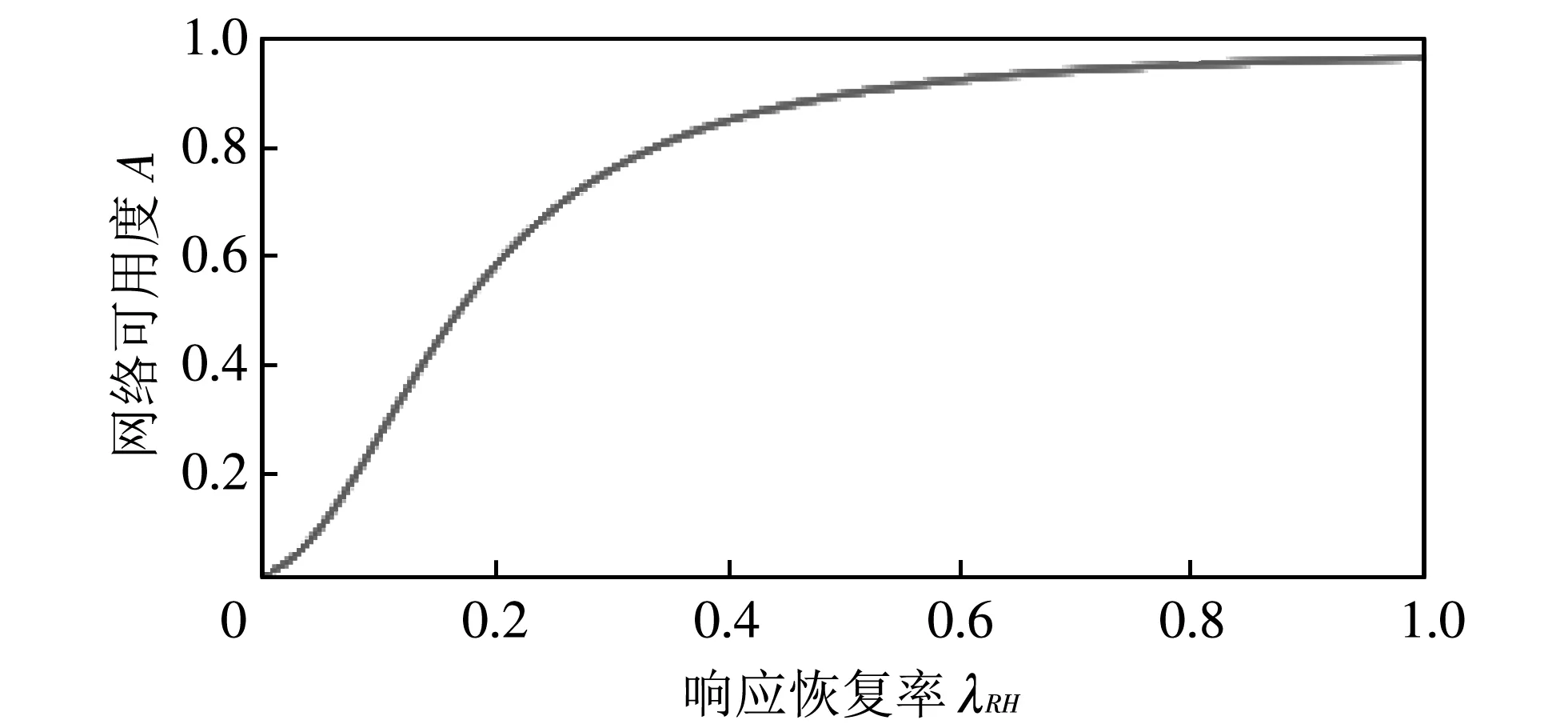
(c) 响应恢复率λRH从0变化到1

如图 11(a) 与图 11(c) 所示，λCR，λRH从0增加到1， 网络可用度逐渐递增. 图 11(a)中(λRH取固定值0.8)，λCR的取值在0～0.5之间， 网络可用度提高最明显， 由0.631 6提升至0.950 3， 提高了0.318 7； 而λCR的取值在0.5～1之间， 可用度基本趋于稳定， 由0.950 3提升至0.963 6， 仅提升了0.013 3. 此实验结果说明， 在攻击程度较轻(λHC=0.1)时，λCR的取值在0.5之后对网络整体可用度的影响不大， 所以在考虑成本的情况下， 检测率并非越高越好.

图 11(c) 中(λCR取固定值0.8)，λRH取值在0～0.5之间， 网络可用度提高最明显， 由0.011 58 提升至0.904 4， 提高了0.892 9； 而λRH的取值在0.5～1之间， 可用度基本趋于稳定， 由0.904 4提升至0.973 3， 仅提升了0.068 9. 从以上实验结果可以看出， 同样是在考虑成本的情况下， 响应恢复率并非越高越好.

另外， 在图 11(b) 中， 随着λHC的增加， 网络可用度迅速下降. 这一结果说明， 被攻击的节点越多， 网络可用度越低， 这与网络实际情况一致. 值得注意的是， 从图中可以看到， 网络络可用度最终并未降为0(λHC=1时)， 这是由于网络中响应恢复机制的作用， 即使妥协率很高， 可用度最低降至0.159 9， 不会为0.

3.3.5 WSNs可生存度

图 12 中分别显示了转化率λCR、λHC、λRH逐渐增加的情况下， 整个网络的生存度变化曲线. 三个图中的整体变化趋势与图 11 类似，λCR,λRH从0增加到1， 网络生存度逐渐递增， 而随着λHC的增加， 网络生存度迅速下降.

具体地， 图 12(a) 中，λCR的取值增加， 对网络整体的可生存度影响并不大， 从最初的0.631 6提升至0.747 3， 提升了0.115 7. 而上一实验中， 可用度的提升度几乎是其三倍. 这是因为， 节点处于健康状态、 妥协状态和响应状态时都被认为是可用的(详见2.4节)， 而我们假设节点只在健康和妥协两个状态时是可生存的， 故网络的可生存度提升值和最高值都达不到可用度的水平. 由图 12(c) 可以看到，λRH的取值在0.2之前， 网络的可生存度都接近0， 在0.2之后才开始提升， 最终提升至0.837 7， 共提升了近0.837 7. 这就说明λRH的取值对网络可生存度的影响较大， 从响应状态向健康状态的恢复率较低时， 对网络可生存度几乎没有影响， 只有大幅度提高恢复率， 才能对网络可生存度有较大提升， 即只有将处于响应状态的节点尽量恢复到健康状态， 网络才能有较高的可生存度. 同时可得出结论， 要提高网络可生存度， 提升网络恢复率比提升检测率更有效果.

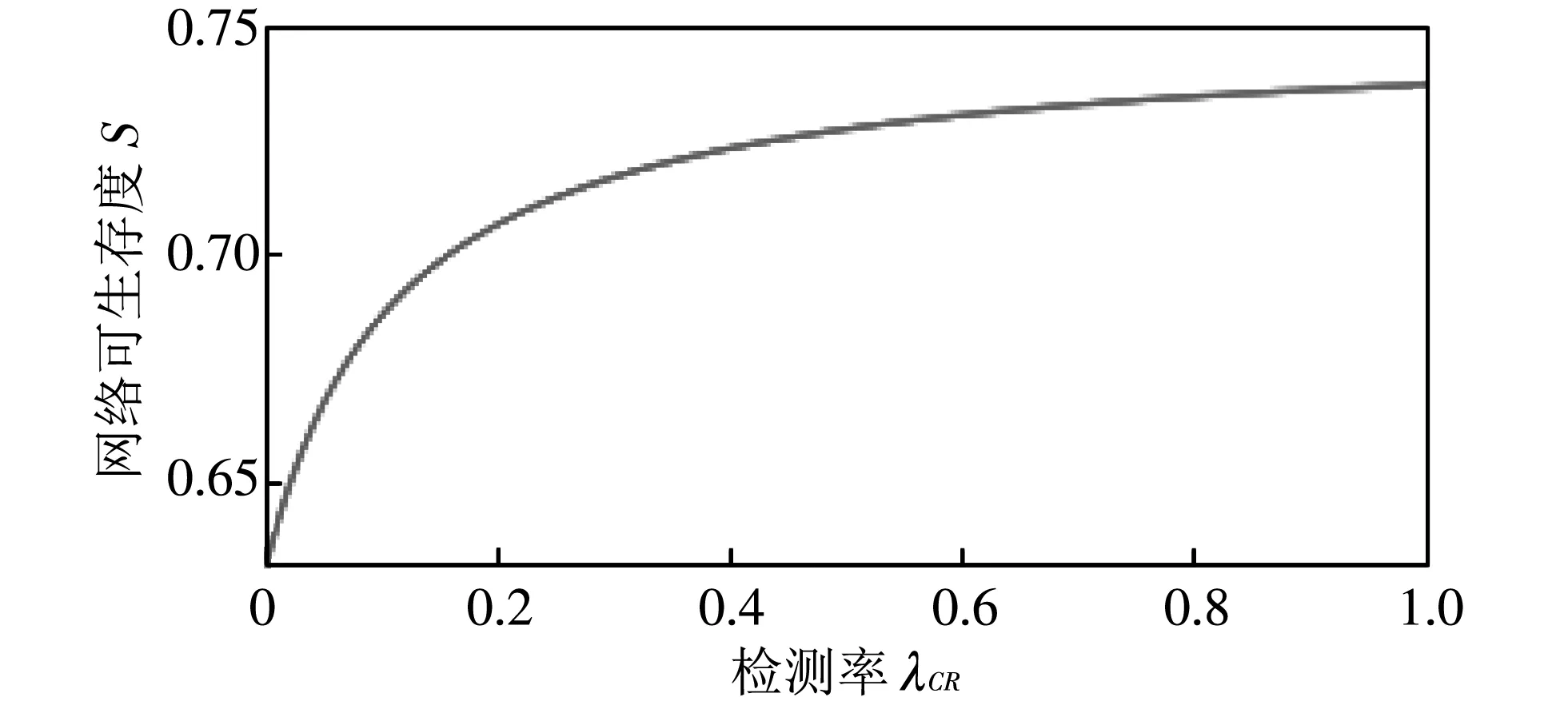
(a) 检测率λCR从0变化到1

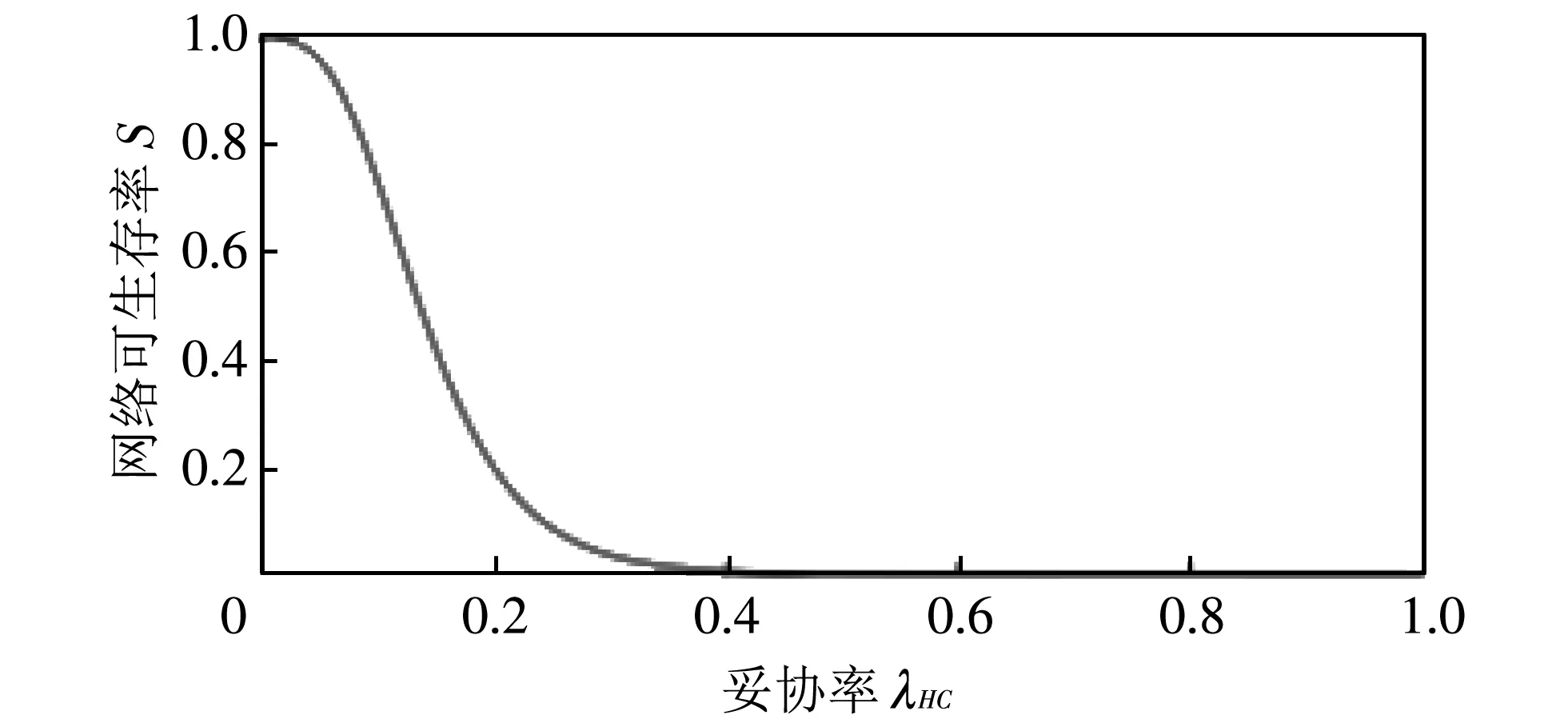
(b) 妥协率λHC从0变化到1

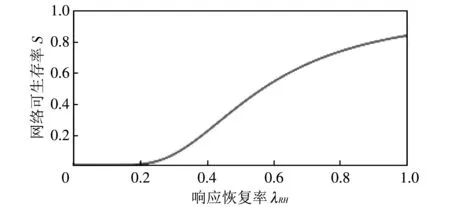
(c) 响应恢复率λRH从0变化到1

在图 12(b)中， 随着λHC的增加， 网络可生存度迅速下降. 这一结果说明被攻击的节点越多， 网络可生存度越低， 这与网络实际情况一致.

此外， 图 12(b) 中， 网络可生存度在妥协率λHC=0.5之后逐渐趋近于0， 而在图11(b)中网络可用度最终也不会为0. 这是因为妥协率越高， 网络中处于状态C的节点越多， 进一步进入状态R的节点也就越多， 模型中考虑网络节点在状态H与C时可提供服务， 状态R时不可提供服务， 而在R是可用的， 所以得到的可用度的值整体高于可生存度.

4 结 论

本文提出基于连续时间马尔可夫链的WSNs可生存性量化评估模型. 该模型给出了遭受恶意节点攻击的WSN状态转换过程， 并对各状态进行稳态分析. 通过该模型计算出单个节点的可靠度， 并在考虑独立失效与相关失效两种情况下， 根据单节点可靠度计算了整个网络的可靠度. 根据各状态的稳态概率对单节点及整个网络的稳态可用度、 生存度进行了定量评估. 最后， 利用仿真实验对模型进行了验证， 并考查了检测率、 恢复率等的变化对各项评价指标的影响. 实验结果表明， 提出的模型能够有效评估WSNs的可生存性， 并且为今后设计高生存性的WSNs提供了依据.

今后， 研究重点将主要聚焦在WSNs可生存性增强方法及技术上， 例如： 安全路由、 入侵检测、 响应恢复等， 以进一步提高网络提供可靠服务的能力.