参数优化VMD在爆破振动信号分析中的应用
杨宗林, 熊继军,2
(1. 中北大学 仪器科学与动态测试教育部重点实验室, 山西 太原 030051;2. 中北大学 电子测试技术重点实验室, 山西 太原 030051)
近年来, 国内外学者研究爆破振动形成的原理以及传播特性, 主要集中在爆破振动形成原因、 现场爆炸实验、 信号监测和不同介质传播规律等方面. 由于爆破振动激发与爆破振动信号瞬时性、 随机性以及传播介质的复杂性等众多因素的影响, 目前的研究中尚未有严格的理论来解释爆破振动信号的传播规律, 而在爆破振动信号分析及分析方法上面解释其传播规律具有重大的意义. 爆破振动信号也属于非线性、 非平稳信号, 而EMD具有较好的自适应性且摆脱了Fourier理论的约束, 在处理非线性非平稳信号方面, EMD具有优秀的时频分析能力[1], 因此, 在非线性非平稳信号分析上应用越来越广泛.
虽然EMD在处理非线性非平稳信号方面具有优异的性能, 但也存在端点效应与模态混叠的问题以及没有严格的数学支撑等不足[2]. 目前, 采用VMD[3-4]替代EMD把非递归、 变分模态分解的形式作为新的分解信号的方式, 克服了模态混叠以及没有严格数学表达式的缺陷. 然而, 变分模态分解也存在缺陷, 如: 参数模态分解个数K与惩罚因子α需要经验预设, 而模态分解个数K设置不正确会直接导致分解结果错误, 惩罚因子α需要经验预设, 太高会引起模态混叠, 太低则结果不准确[5].
综上所述, 本文提出一种基于幅值谱的混合遗传-粒子群算法[6-8]对模态分解个数K与惩罚因子α进行参数优化, 并应用到爆破振动信号分析中. 首先, 应用混合遗传-粒子群算法适应度函数选取出模态分解个数K与惩罚因子α以求解幅值谱熵[9-10]; 然后, 将最优的参数组合[K,α]作为VMD预设参数;最后, 利用相关性系数[11]检验对应模态分解个数K的正确性.
1 变分模态分解
变分模态分解[12]本质是若干个维滤波器构成的一种全新自适应、 完全非递归的模态变分与信号处理算法, 在处理非平稳、 非线性信号上具有良好的性能. 首先, 构造出变分问题模型, 将原始信号f分解成K个具有中心频率的有限带宽的模态分量, 并且使得各模态分量估计带宽总和最小, 把原信号等于所有模态分量叠加总和作为约束条件, 因此, 相应约束变分表达式[12]为
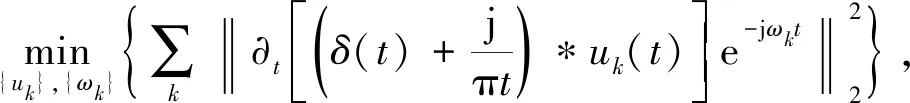
(1)

(2)
式中:K为模态分解个数; {uk}为分解后第k个模态分量; {ωk}为分解后第k个中心频率;δ(t)为Dirichlet函数; *是卷积运算.
为了求解式(1)和式(2), 此处引入惩罚因子α与Lagrange乘法算子λ, 构造增广Lagrange函数, 约束变分问题则被转变成非约束变分问题[12], 因此
L({uk},{ωk},λ)=

(3)
对式(3)中的Lagrange函数进行Fourier变换, 找出对应极值解, 则能推出对应的模态分量uk与中心频率ωk, 因此
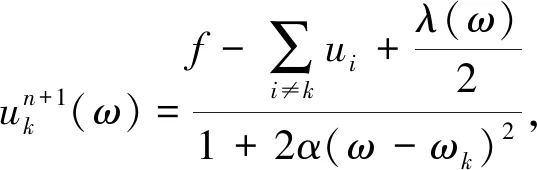
(4)

(5)
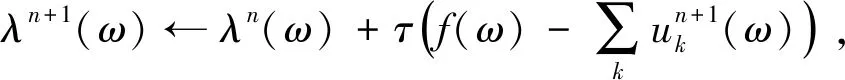
(6)
式中:τ为噪声容忍度, 即双重上升的时间步长, 如不是以重建为目的的分解, 通常可设为零. 选取交替方向惩罚算子ADMM求解约束变分模型的最小值, 则观测信号被分解成了K个模态分量. 分解过程的算法步骤[12]如下:
3) 应用式(6)更新λn+1;
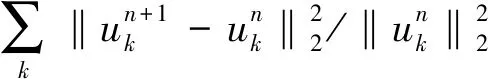
2 VMD参数优化
2.1 VMD参数分析
考虑到VMD尚无成熟的理论来计算模态分解个数K与惩罚因子α, 因此只能凭借经验预设模态分解个数K与惩罚因子α, 预设不准确会导致模态分解对信号评价的失误.
由于振动信号特征分布的稀疏程度可以通过幅值谱熵数值变化来反映. 而VMD分解的模态分量uk的信噪比与有效特征所表现的规律性冲击响应成正比, 因此该模态分量uk的稀疏特性随着信噪比的递减而减弱, 递增而增强, 相应的幅值谱熵随信噪比递增而递减, 递减而递增. 因此, 本文通过对VMD分解后的模态分量uk进行Fourier变换得到幅值谱, 结合幅值谱公式[13]与信息熵[14]公式推导出
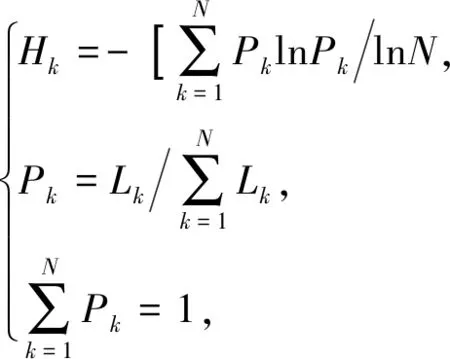
(7)
式中:Hk为VMD分解模态分量uk的幅值谱熵;Lk为VMD分解第k个模态分量uk做Fourier变换后所得幅值谱;N为模态分量uk的信号长度. 考虑到VMD需要凭借经验预设模态分解个数K与惩罚因子α, 随机选取参数组合[K,α]并进行VMD模态分解, 代入式(7), 将K个幅值谱熵最小值minHk作为该参数组合[K,α]的局部极小值, 显然, 与局部极小值对应的模态分量uk是该参数组合[K,α]包含冲击振动特征信息最多的模态分量, 即最佳分量. 因此, 对参数组合[K,α]的最优参数估计问题转化为求解幅值谱熵局部极小值的最小值的优化问题.
尽管变分模态分解解决了经验模态分解的模态混叠与没有严格数学推导的缺陷, 但变分模态分解仍然存在端点效应的问题. 因此, 本文引入传统的波形镜像延拓的方法, 以减少端点效应带来的影响.
2.2 基于幅值谱的混合GA-PSO算法波形镜像延拓VMD参数优化
遗传算法(Genetic Algorithm,GA)与粒子群优化算法(Particle Swarm Optimization, PSO)都是经典的智能优化算法, 利用GA算法的全局搜索能力强以及收敛性好和PSO算法收敛速度快的优点, 将两者串联混合能够克服GA算法收敛速度慢和PSO算法容易陷入局部收敛的缺陷, 实现优势互补克服了两者的局限性. 过度分解或过度惩罚也会使熵最小, 因此, 本文通过引入混合GA-PSO算法[15]分别对模态分解个数K与惩罚因子α交叉优化, 利用VMD求解幅值谱熵局部极小值的最小值进而求出最佳的模态分解相应的参数组合[K,α], 步骤如下:
1) 将幅值谱熵的局部极小值minHk作为适应度函数, minHk越小则模态分量蕴含的特征信息越多, 因此目标函数为min(minHk);
2) 利用随机数初始化PSO粒子位置、 粒子速度与GA种群, 确定GA与PSO的所有参数;
3) 对观测信号进行波形镜像延拓;
4) 根据式(7)计算适应度值;
5) 当m代GA进化后, 把GA种群的个体作为PSO的初始粒子;
6) 当n代PSO进化后, 再把PSO个体的局部最优解赋给GA个体;
7) 计算完预设最大迭代次数后, 对信号进行波形镜像延拓, 预设合理的二次惩罚因子, 在惩罚因子的基础上对模态分解个数进行搜索优化, 返回幅值谱熵局部极小值的最小值作为判定标准, 找出最佳的模态分解个数K;
8) 在最佳模态分解个数K基础上, 以同样的方式搜索优化惩罚因子α, 最终得到相应的最优参数组合[K,α].
至此, 对利用最优参数组合[K,α]作为VMD预设模态分量个数与二次惩罚因子进行变分模态分解, 具有了一定的理论依据, 避免了模态混叠和计算的盲目性.
3 仿真信号分析
为了验证算法的有效性, 通过构造解析函数式(8)并嵌入方差为0.5的高斯白噪声时域信号进行模态分解对比, 信号如图 1 所示.
x(t)=6t2+cos(4πt+10πt2)+

(8)

图 1 仿真信号Fig.1 Simulation signal

图 2 EMD分解结果

图 3 VMD分解结果

图 4 EMD和VMD去噪Fig.4 EMD and VMD denoising
图 2 和图 3 分别为EMD和VMD分解结果. 由图 2 可以看出, EMD分解结果模态混叠严重, IMF1为高频高斯白噪声, 除去IMF1重构信号的结果如图 4 所示. 图 3 显示VMD对各分量的分解还原度很高, 解决了模态混叠, 并且抗噪能力很强, 同样IMF1为高斯白噪声, 其滤波效果如图 4 所示. 从仿真结果可以看出, 本文提出的优化参数的VMD模态分解效果好, 抗噪能力强, 还原精度高, 交叉优化的方法能准确地得出模态分解个数以及惩罚因子, 抑制了虚假分量.
4 爆破振动信号分析
爆破振动信号也属于非线性非平稳信号, 传统Fourier分析及其推广方法对处理此类信号存在精度不足等问题, 而基于模态分解的时频分析方法在处理此类信号时表现优异, 而传统的经验模态分解存在端点效应、 模态混叠、 虚假分量以及无严格理论证明等问题, 本文所提出的基于幅值谱的GA-PSO交替优化以及采用镜像延拓处理边界的变分模态分解, 抑制了模态分解带来的模态混叠、 端点效应及过度分解无意义的虚假分量的问题, 并且克服了传统经验模态分解无严格理论证明的缺陷. 为了验证本文提出的方法的优越性, 以某型TNT在钢箱梁上起爆的爆破冲击振动试验的冲击振动信号为例来分析(采样频率为200 kHz, 如图 5), 步骤如下:
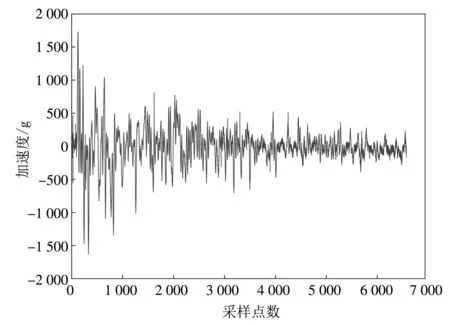
图 5 典型爆破振动信号Fig.5 Typical blasting vibration signal
1) 利用随机数初始化PSO粒子位、 粒子速度与GA种群, 确定GA与PSO的所有参数;
2) 对冲击振动信号进行镜像波形延拓;
3) 采用随机初始化参数进行初次VMD分解, 计算IMF分量的幅值谱熵, 得出局部最小值;
4) 利用GA-PSO寻优求出局部最小值中的最小值, 进而得出相应的模态分解个数及惩罚因子, 确定正确模态分解个数后, 固定模态分解个数, 对惩罚因子再次进行步骤3)的操作, 找出最优惩罚因子;
5) 利用相关系数法验证是否存在过分解的问题.

图 6 原信号EMD分解结果及其模态分量频谱Fig.6 EMD decomposition result of original signal and its modal component spectrum
由图 6 可以看出, 模态分量IMF1的频率最高, 然而所占的能量最小, 是测试环境下的高频噪声, IMF2~IMF6模态混叠严重, 求取各分量与原信号的相关系数为 0.120, 0.6, 0.525, 0.459, 0.316, 0.148, 0.067, 0.034, 0.063. 对比相关系数和频谱图可以看出, IMF7~IMF9为虚假分量. 使用基于幅值谱熵的混合GA-PSO算法改进的VMD得出最优参数组合为[1 543,5], 图 7 为VMD分解结果, 由图能够清晰地看出信号内包含的频率成分, 求取各分量与原信号的相关系数为0.107 1, 0.456 9, 0.552 6, 0.555 2, 0.649 8, 均在同一数量级下, 没有出现虚假分离. 对比EMD的分解结果, 本文所提出的改进的VMD方法, 很好地解决了端点效应、 模态混叠以及虚假分量的问题, 并且具有坚实的理论基础, 从而验证了本文提出算法的有效性, 并且在复杂的环境下, 算法优化的参数仍然保持稳定性.

图 7 原信号改进VMD分解结果及其模态分量频谱Fig.7 Improved VMD decomposition result of original signal and its modal component spectrum
5 结 论
本文通过变分原理使各模态与中心频率不断更新调整, 使VMD相对于EMD具有更好的自适应性, 也是爆破振动信号进行模态分解的有效方法, 解决了EMD模态混叠及没有严格的数学支持的缺陷, 分析效果更明显、 有效. 本文对VMD存在经验性预设模态分解个数与惩罚因子的缺陷, 提出了一种基于幅值谱熵的混合GA-PSO算法对参数进行最优估计, 从幅值谱熵的数值反映振动信号特征分布的稀疏程度角度进行了最优参数估计, 并且针对组合优化的方式提出了模态分解个数与惩罚因子交叉优化的方法, 改善了搜索优化过度分解或过度惩罚的问题, 并且相对以往凭借经验估计参数的方法具备了科学性, 同时有效解决了模态混叠以及繁琐的人工经验尝试的不足. 在复杂爆破振动信号应用上, 有效抑制了模态混叠的问题.
爆破振动波波形包含重要的爆破参数信息, 而爆破振动波在传播过程中的时频特性和爆源条件、 传播介质、 地形等因素密切相关, 因此使用参数准确的VMD方法处理爆破振动信号能够有效提取精确的IMF分量的时频特征, 实现爆破振动信号的精确分析处理, 这对研究爆破振动波的作用机理、 传播规律、 振动控制等具有重要意义.

