动力增程型高超声速飞行器的再入轨迹规划

冯玥，王容顺，梅映雪，孙洪飞，吴了泥

（厦门大学 航空航天学院，厦门361102）

近年来，高超声速飞行器凭借其飞行速度快、射程远和突防能力强等优势，在军事和民用方面普遍受到重视。高超声速飞行器的再入返回过程一般是无动力返回，而动力增程型高超声速飞行器是一类某种携带少量燃料动力装置（助推器）的飞行器。再入过程中飞行器的速度或高度减小到一定值之后，助推器点火对其进行加速补能，从而达到增加航程的目的。由于燃料有限，飞行过程中如何分配助推器的点火时机、点火次数以及点火时长以达到最远的航程，从而使燃料利用率最高，是动力增程型高超声速飞行器需要研究的新问题。

高超声速飞行器的再入过程［1］速度大，受热流、动压和过载等过程约束，一般还具有高精度的末端约束，因此轨迹设计是再入返回的关键部分。20世纪30年代德国科学家Sanger和Bredt提出拟平衡滑翔概念［2］，1948年钱学森提出了著名的钱学森弹道，为飞行器轨迹规划问题的研究奠定了基础。Lu［3］、卢宝刚［4］、张科南［5］等基于拟平衡滑翔条件提出多种轨迹规划的方法；此外，国外Rao［6］、Elangar［7］等以及国内呼卫军［8］、雍恩米［9］等基于伪谱法将再入轨迹规划问题转化为最优控制问题进行求解；近年来，宋超［10］、杨鹏宇［11］等分别在轨迹优化基础上考虑了航路点约束问题和故障下的在线轨迹重构问题。根据建模与求解的特点，飞行器轨迹规划问题可以视作非线性、带有状态约束和控制约束的最优控制问题，采用最优控制方法进行求解是自然的选择。

对于动力增程型这样的新型高超声速飞行器，国内外对其轨迹规划问题的研究缺少相关文献。在美国学者Carter等［12］的研究中，证实了高超声速飞行器的周期跳跃弹道可以实现减少燃料消耗从而增大航程的目的。该周期弹道通过助推器脉冲点火来维持飞行器跳跃运动的平均高度，在跳跃弹道波谷点火弥补能量消耗，最终调整飞行器状态使其达到与上一周期相同。国内蔺君等［13］提出了改进的高斯伪谱法（Gauss Pseudospectral Method，GPM），主要解决了分段轨迹规划的连续性问题，但将动力装置的点火次数和点火时长设为已知量不作求解，动力装置的增程作用也没能显现。

本文针对动力增程型高超声速飞行器的再入模式展开研究，发现GPM求解变量多、约束强，解算耗时长甚至难以收敛；而周期跳跃弹道具有周期形式的强约束条件，动力装置的启动方式以及飞行器在各个周期的状态均固定，难以灵活协调助推器燃料利用率和弹道航程大小的关系。因此，本文从周期跳跃弹道增程的本质出发，将周期跳跃弹道的强约束去除，重新研究动力装置启动的最佳时机和方式，综合考虑弹道末端落点的精度，提出一种新的动力增程型高超声速飞行器再入模式，并在该模式下提出了一种能量损失缓慢的“打水漂”弹道形式。

1 预备知识

1.1 动力学模型

1.1.1 动力学方程

由于高升阻比特性，高超声速飞行器再入阶段的气动力和地球重力分别约为科氏惯性力和地球自转引起的惯性离心力的100倍和1 000倍［8］，因此可以假设地球为圆球不旋转模型，进而得到无量纲三自由度运动方程［14］为

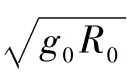
无量纲升力L、阻力D分别为

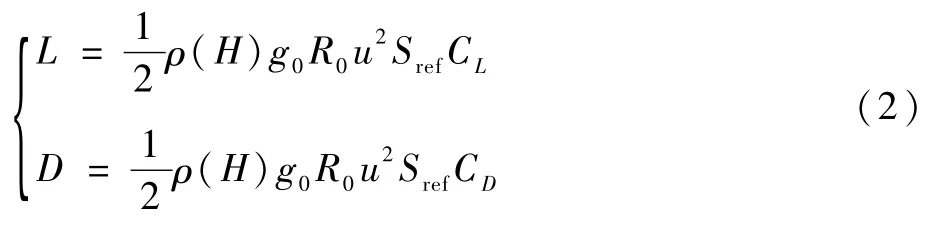
式中：Sref为飞行器气动参考面积；CL、CD分别为升力系数和阻力系数，通常由飞行器的迎角α和马赫数决定；ρ（H）为大气密度，H为海拔高度。

本文大气密度模型采用式（3）计算：

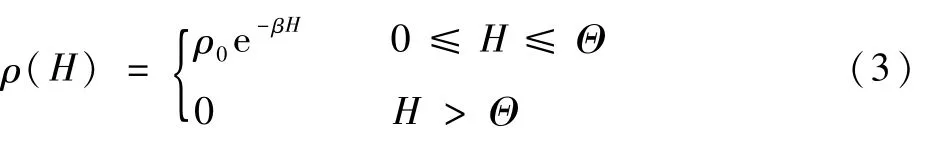
式中：β为决定大气密度指数衰减的常数；ρ0为海平面的大气密度；Θ为常值。

1.1.2 控制量

在高超声速飞行器动力学方程（1）中，迎角α、倾侧角υ和助推器点火产生的推力F为3个控制量，作为模型的输入。为满足飞行器控制能力要求，一般有如下约束形式：

式中：αmax、αmin为攻角取值范围的上、下限；κ为倾侧角取值范围的上、下限的绝对值；Is为助推器的比冲；tb和mb为助推器工作的总时长和助推器携带燃料的总质量。

1.2 问题描述

在本文动力增程型高超声速飞行器再入模式的研究中，需要解决的问题是设计合理的控制量，使航程尽可能得大。没有输入量F的情况下，上述问题可看作无动力返回的轨迹规划问题，工程上普遍使用GPM来求解最优控制问题的数值解。输入量F的存在使轨迹规划问题复杂化，助推器点火的时机、点火次数以及每次点火持续的时长均需要设计，此时GPM 求解难度大，算法不易收敛；而周期跳跃弹道不能合理利用助推器点火补偿的能量。再有，单纯的跳跃弹道在末端由于跳跃势必会影响末端落点精度。如何利用“点火次数”、“点火时机”、“点火时长”和“末端落点精度”这4个因素来设计动力增程型再入弹道是本文主要的研究内容。

2 再入弹道的解析解

下面分析助推器无点火情况下再入弹道的解析解形式，以此作为提出动力增程型再入弹道轨迹规划策略的理论依据。

飞行器再入弹道的解析解一般难以获得，通常需要相当苛刻的假设条件，为得到再入弹道的航程解析解，需做如下假设：

假设1飞行器在大气层内运动空域假设处在同温层，空气密度变化为式（3）所示，大气层边缘距地面为常值Θ（称距地球表面高度超过Θ的空间为“大气层外”）。

假设2地球为质量分布均匀的不旋转圆球体，忽略地球自转。

假设3飞行器飞行中保持侧滑角为零，倾侧角为常值，即飞行器在某个纵向平面飞行。

假设4飞行器在Sanger弹道的跳跃阶段大气层内所受空气动力作用远大于重力作用。

定义1以飞行轨迹点不再出大气层的起点为分界点，整个再入过程以此分界点为界，被分为2个阶段。该分界点前的再入轨迹称作“再入前期”，该分界点后的再入轨迹称作“再入后期”。

图1为不考虑助推器点火的情况下，高超声速飞行器再入弹道的示意图，图中V0和θ0分别为飞行器第1次离开大气层的初始速度和初始弹道倾角；G点为再入前期与再入后期的分界点，设G点处是飞行器第N次进入大气层，那么由定义1可知，再入前期飞行器共进入大气层N次。

图1 再入弹道Fig.1 Reentry trajectory

2.1 能量转换分析

在假设2前提下，研究助推器不工作情况时飞行器的受力情况和能量转换，则再入过程中以下2个事实显然成立。

1）飞行器在大气中仅受3个力作用，分别是空气阻力、升力以及重力。由各个力的方向与速度方向的角度关系可知，阻力始终做负功、升力不做功、重力虽然做功但不改变飞行器的机械能。

2）飞行器进入大气层后由于空气阻力的作用，速度和动能逐渐减小，此时影响机械能的唯一因素是空气阻力。也就是说，飞行器由起点到终点的运动过程中，动能的消耗都用来克服空气阻力做功。

结合式（3）的大气密度模型，由事实1）和2）可知，当V0和θ0以及末端速度、高度固定，飞行器可以通过多次跳出大气层使能量消耗缓慢，从而达到增程的目的。

由定义1可知，飞行器在再入后期阶段不再跳出大气层。可见，再入前期的轨迹设计是动力增程型再入弹道的关键部分，下面推导再入前期弹道的解析解。

2.2 Sanger弹道解析解

再入前期弹道可近似为Sanger弹道，关于Sanger弹道的解析解形式文献［12，15］已有研究，现作如下总结。

如图1所示，将弹道的每一次跳跃分为2种轨迹：称每一次穿越大气层时对应大气层外的轨迹为弹道轨迹（Ballistic Trajectory）；相应地称大气层内的轨迹为跳跃轨迹（Skip Trajectory）。2种弹道由于物理特性不同需分别求解，那么再入前期的总航程角解析解可以表示为2个航程角分量的和，如式（5）所示：

式中：Vs为第一宇宙速度；Φt为总航程角；g为引力加速度；n为飞行器进入大气层的次数。

由航程Rt与航程角Φt的关系Φt=Rt/R0，可得到再入前期弹道的总航程解析解。推导过程如下：

令

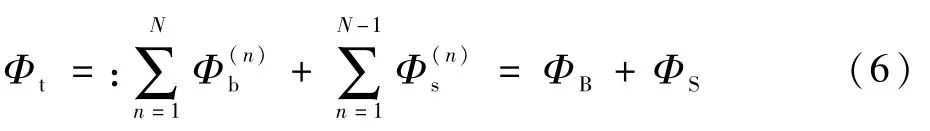
为方便叙述，以下约定变量的下标e和d分别指进入大气层和跳出大气层，n作上标表示次数。

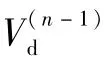
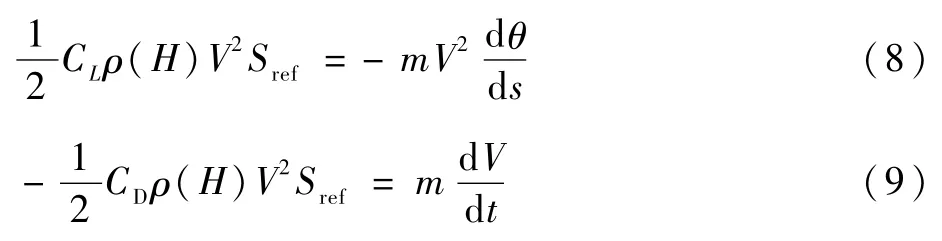
式中：dθ／d s=-1／rc，rc为地球曲率半径，s为航程。

将d H／d s=-sinθ与式（3）代入式（8）中，并对θ进行积分有

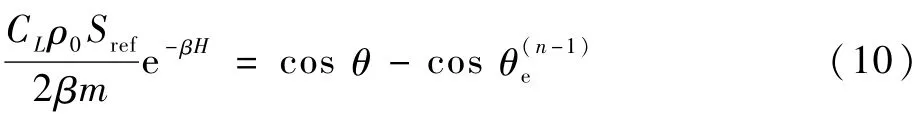
将d s／d t=V代入式（9）中，并对s进行积分，有

结合假设1，不难得到

则式（11）变为

最终，结合式（7）、式（12）和式（13），可知Sanger弹道N个弹道轨迹总航程角为

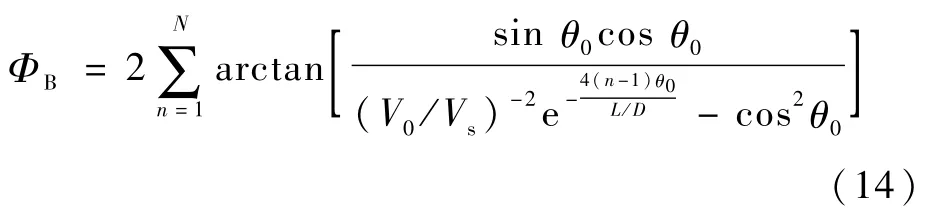
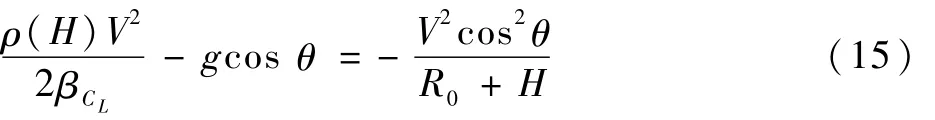
取R0＋H≈R0，将式（15）表示为密度的方程为

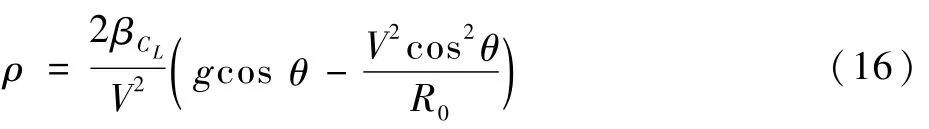
由式（10）可知，跳跃轨迹上的点与起点满足如下规律：

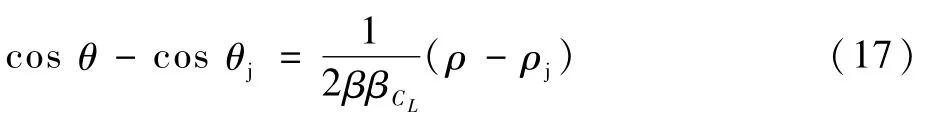
在波谷点有θv=0。取θ=θv，将式（16）、式（3）代入式（17），求解可得

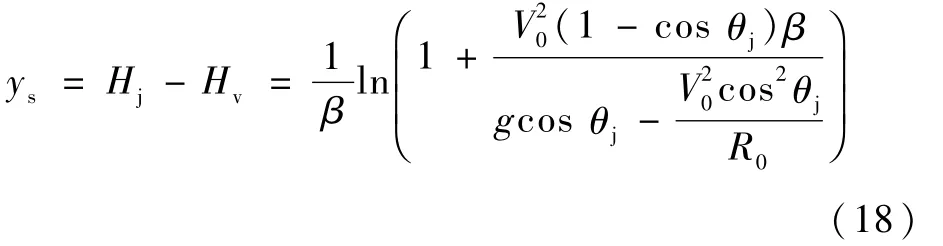
式中：ys=Hj-Hv为跳跃深度。

当跳跃深度最大时，假设满足如下关系式：

那么第1个跳跃轨迹航程的最大值可近似表达为

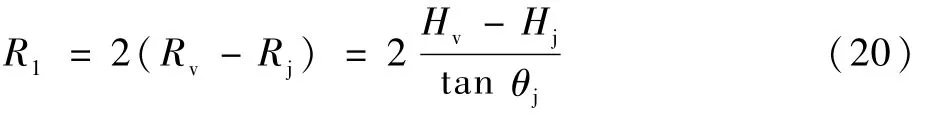
式中：R1为第1个跳跃轨迹的航程。

将式（18）代入式（20），进而得到第1个跳跃轨迹的最大航程角为

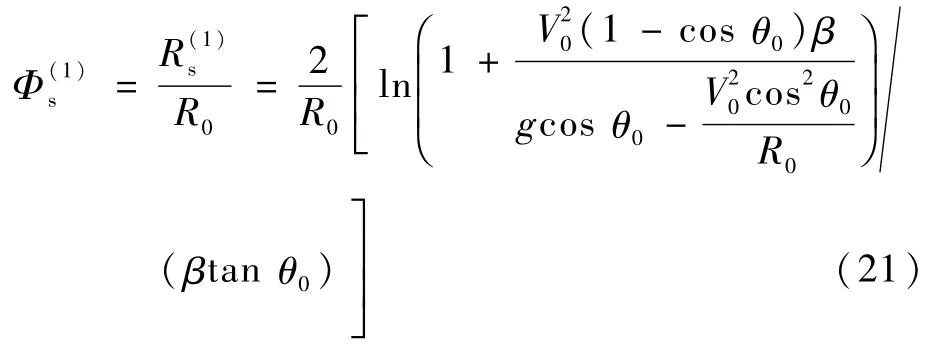
类似地，结合式（12）和式（13）可以得到Sanger弹道全部N-1次跳跃轨迹的总航程角为

将式（14）与式（22）代入式（6），即可得到Sanger弹道总航程角的解析解。至此，式（5）的推导完毕。

注1对式（5）进行分析可知，Sanger弹道的航程完全取决于V0、θ0以及飞行器的升阻比；在不超过第一宇宙速度的前提下，初始速度越大航程越大，同时升阻比越大航程也越大。因此，再入前期弹道轨迹的最大航程一定是在合适的初始弹道倾角、最大升阻比和最大初始速度的条件下实现。

3 动力增程型弹道再入描述

为给出动力增程型高超声速飞行器再入模式，将整个再入过程分为再入前期和再入后期2个阶段，根据设计目标的不同，需要分段进行规划。再入前期通过助推器点火形成等高类周期跳跃弹道，利用注1结论得到动力装置的启动方式，保证了航程最远；再入后期采用拟平衡滑翔形式，解决了跳跃弹道带来的难跟踪、机动性能差以及落点精度低等问题。

针对以上描述，给出如图2所示的动力增程型弹道再入模式（记第i次上升至波峰的点为Pi）。下面将分别介绍再入前期和再入后期的弹道特征以及需要解决的问题。

图2 动力增程型弹道再入模式Fig.2 Range-extended trajectory reentry mode

3.1 再入前期

为了方便对再入前期弹道进行研究，除上述提出的假设外，还需做以下补充：

假设5地面推进系统已经足够好，其能够保证飞行器在最佳初始弹道倾角状态脱离，顺利将其送至预定最大高度，在达到最大高度前，助推器无需点火。

假设6助推器所携带的燃料充足，产生的推力为常值推力，其方向与飞行器空速方向的夹角为0°。

设Vc为高度Θ 处的临界速度，它代表飞行器在该高度下能够绕地球飞行的最大速度，这个值略低于第一宇宙速度，超过速度Vc飞行器将脱离地球引力束缚。

根据2.1节可以知道，再入前期的轨迹需采用跳跃弹道，在该阶段助推器点火，使飞行器尽可能多地跳出大气层，从而减少能量消耗，获得更远的航程。

弹道初期为等高类周期跳跃弹道，助推器点火结束后，弹道呈现自由跳跃的Sanger弹道形式。该阶段的轨迹规划策略是基于弹道解析解得到的，研究动力装置的最佳启动方式（包括助推器的点火次数nb、点火时刻τi以及单次点火时长σi，带下标i的物理量表示其第i次点火的值，i=1，2，…，nb）是该阶段弹道设计的难点。

3.1.1 等高类周期跳跃

如图2所示，等高类周期是指该阶段弹道的每个相位周期都具有相同最大高度。助推器的点火发生在此阶段，高度限制的存在使得助推器的燃料不能在第一次点火时全部耗尽，因而出现等高类周期跳跃的形式，类周期重复的次数由助推器所带燃料以及该阶段的最大速度共同决定。

因此，该阶段需要合理设计助推器的工作方式，使得飞行器速度达到临界速度Vc前，每个类周期具有爬升至与发射上升段波峰高度Pt相等的能力，如果无法做到一次性耗尽所有燃料，则下次点火耗尽所有燃料，以此类推，最终形成等高类周期跳跃弹道。

注2助推器点火补能的前提是该阶段的速度不超过Vc，因此，在飞行器速度大于Vc前，助推器能够工作至燃料耗尽；否则应在速度达到Vc时，停止助推器继续工作。

3.1.2 自由跳跃

助推器最后一次点火结束，飞行器由于没有能量补充而呈现自由跳跃，来回穿梭大气层使得飞行器能量逐渐消耗，形成波峰高度逐渐减小的Sanger弹道形式。该阶段的弹道形式可以根据等高类周期跳跃弹道的最大速度是否达到Vc分为两类。

若在上一阶段燃料耗尽，仍不能使飞行器速度达到临界速度Vc，那么由于没有能量补充，速度衰减很快，最终将不再跳出大气层，此时表现为普通的Sanger弹道。若在上一阶段飞行器经多次点火后，速度能够达到临界速度Vc，当轨迹满足一定弹道倾角时，将出现一种特殊的Sanger弹道形式——“打水漂”弹道。该模式下，飞行器以Θ高度的大气层为分界面，进入大气后在极短的时间内“反弹”到大气层外，这种跳跃能量损失少，速度减小缓慢，飞行器能够重复多次这种“打水漂”跳跃，以基本不变的速度飞行足够远的航程，直至速度减小到不足以再跳出大气层，作为再入前期结束的标志。

3.1.3 轨迹规划策略

再入前期的首要任务是保证足够的航程，该阶段再入弹道的轨迹规划需要设计的输入量为迎角α、助推器点火次数nb、助推器点火时刻τi以及每次助推器点火时长σi。

助推器点火次数nb取决于助推器携带的燃料以及等高类周期跳跃弹道的最大速度。结合假设5、假设6和Sanger弹道解析解的结论，再入前期弹道的航程最优一定是在满足以下条件的情况下实现：

条件2 推器点火时刻τi取每个类周期波峰对应的时刻，第1次点火发生在飞行器达到发射上升段的波峰。

在上述条件下，由皮卡-林德洛夫定理可知，助推器每次的点火时长σi有唯一解。

3.2 再入后期

由于再入后期没有助推器的点火过程，待设计的控制量中不用再考虑动力装置的启动参数，问题相对比较简单。

这样看来，再入后期的轨迹规划问题可描述为一个多约束轨迹优化问题，其本质上可以看作最优控制问题，可以使用求解最优控制问题的一般方法来解决，本文使用GPM进行再入后期轨迹优化问题的求解。

下面结合具体约束与性能指标，给出了该非线性规划问题的数学表达形式。

3.2.1 约束形式

再入后期由于没有动力装置的启动，飞行过中以飞行攻角α和倾侧角υ为控制变量。那么，为了满足飞行器控制能力要求，通常有式（4a）、式（4b）的控制量约束形式，此外还需满足式（1）的模型约束［18］。除上述2种约束类型外，本文还考虑了如下过程约束和终端约束。

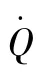
为保证将飞行器以指定的角度、速度和高度到达弹道终端，还需加上如下终端约束：

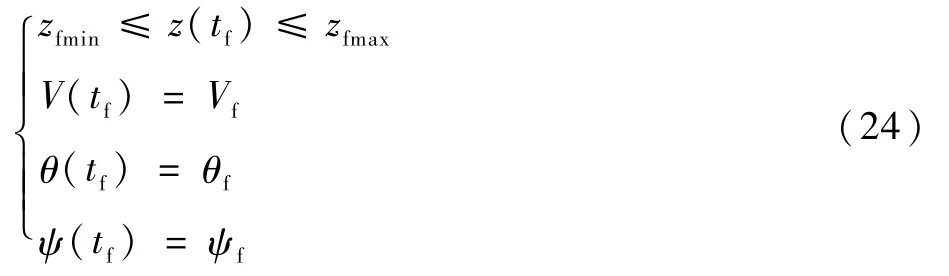
式中：tf为终端时刻，带下标f的物理量表示其在终端时刻的值。

3.2.2 性能指标

再入后期的性能指标综合考虑航程大小和弹道平滑程度。这里采用式（25）作为再入后期弹道的性能指标：

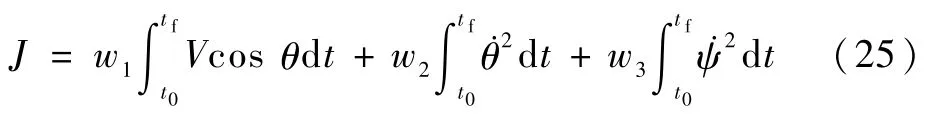
式中：t0为初始时刻；J为性能指标；w1、w2、w3为权重系数，用于调节优化指标中飞行器飞行航程以及弹道平滑性最优之间的权重，且w1、w2、w3满足w1＋w2＋w3=1。

最终，所要研究的多约束问题可描述为：在满足动力学方程约束式（1）、控制约束式（4a）、式（4b）、过程约束式（23）以及终端约束式（24）情况下，寻找合适的状态轨迹和控制输入，使得性能指标式（25）最小。

4 仿真结果及分析

仿真在MATLAB环境下进行，首先给出了燃料充足情况下的动力增程型再入弹道的仿真实现，证实了“打水漂”弹道的可实现性，仿真结果表明本文所提出的再入模式具有足够远的飞行能力；进而将本文提出的动力增程型再入弹道与已有研究做出对比，仿真结果显示，本文提出的再入模式能够充分利用助推器点火补充的能量，使飞行器能够以更少的燃料飞行更远的距离，同时获得更高的末端能量。

4.1 实现流程

第3节中提出的动力增程型弹道再入模式，其计算流程如图3所示，其中x0为状态量的初值。

4.2 动力增程型再入弹道的仿真实现

为验证本文所提出的动力增程型再入弹道的可实现性，在燃料充足的情况下进行仿真验证，仿真参数如下所述。

2）初始状态量：z0=6451004 m，V0=7100 m/s，λ0=0°，φ0=0°，θ0=2.1°，ψ0=0°。

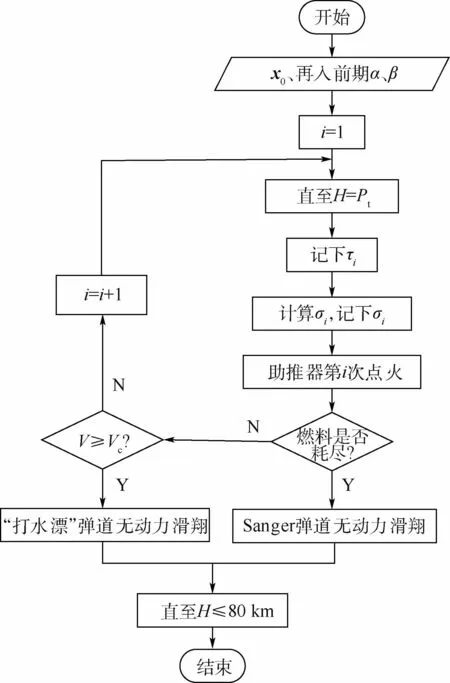
图3 动力增程型弹道再入模式流程图Fig.3 Flowchart of range-extended trajectory reentry mode

图4～图7为该仿真条件下的动力增程型再入弹道的高度、推力、速度、迎角及过程约束随时间的变化。

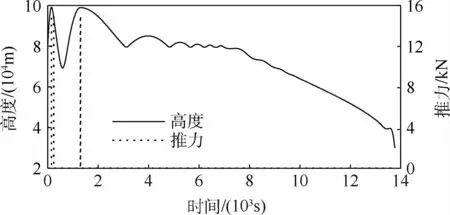
图4 高度、推力随时间的变化Fig.4 Variations of altitude and thrust changing with time

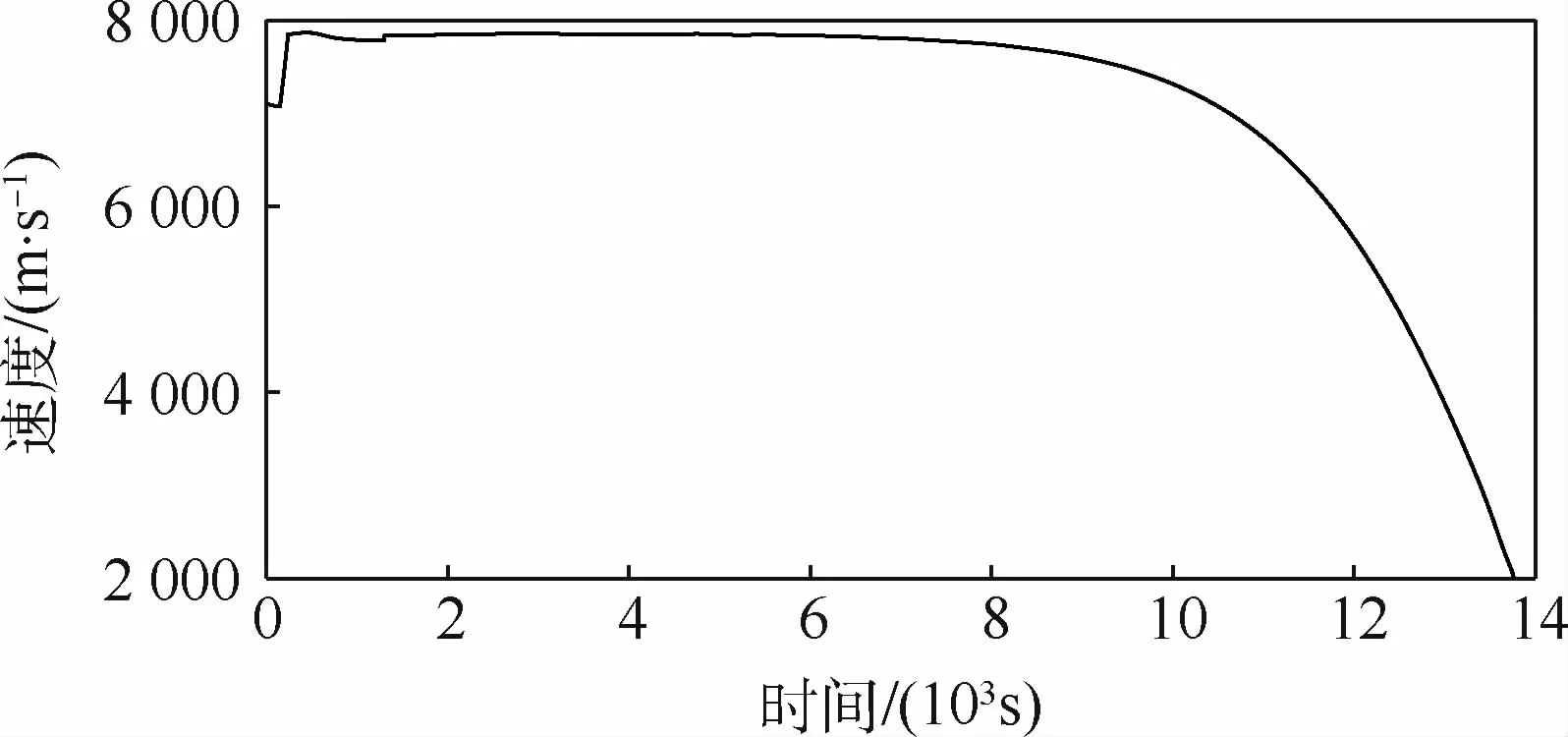
图5 速度随时间的变化Fig.5 Variation of velocity changing with time

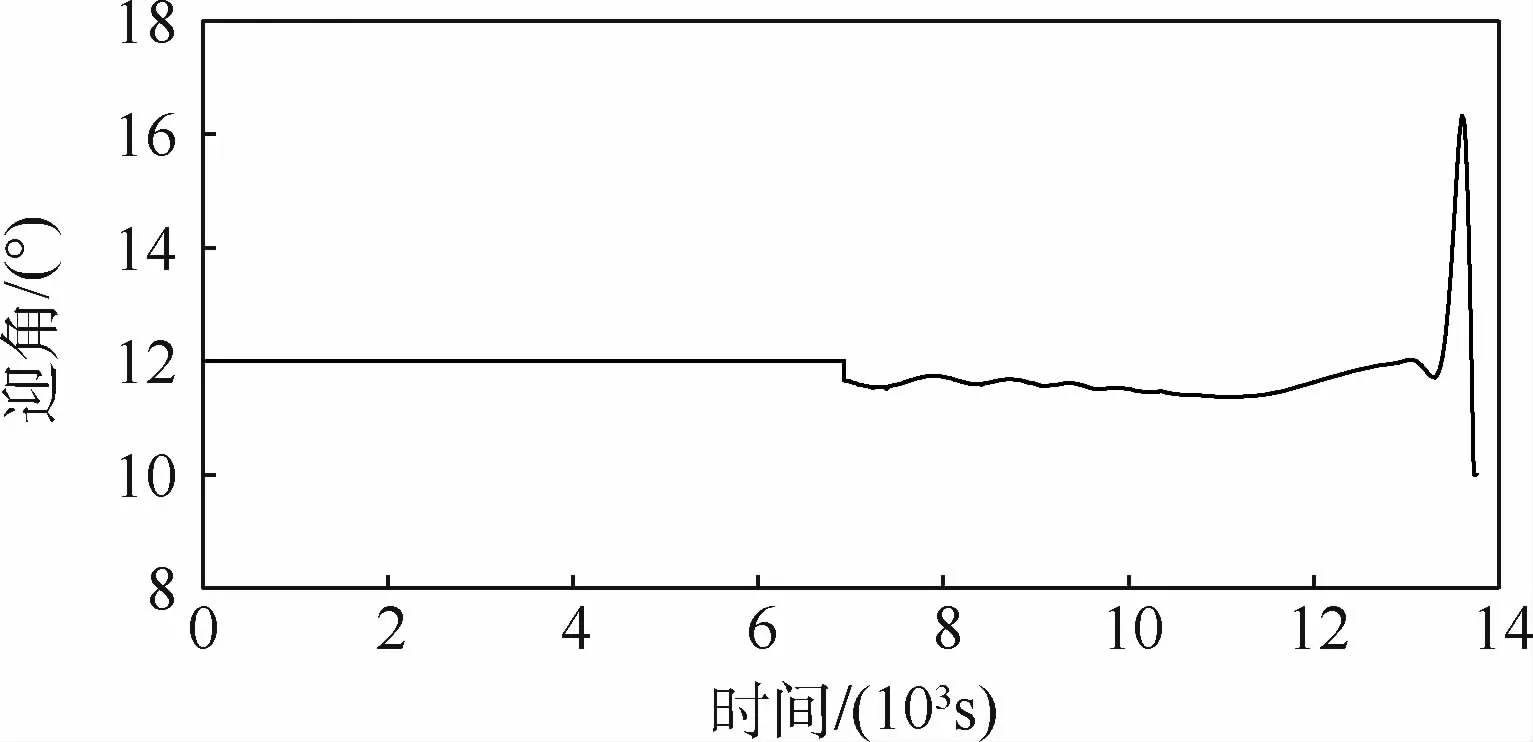
图6 迎角随时间的变化Fig.6 Variation of angle of attack changing with time

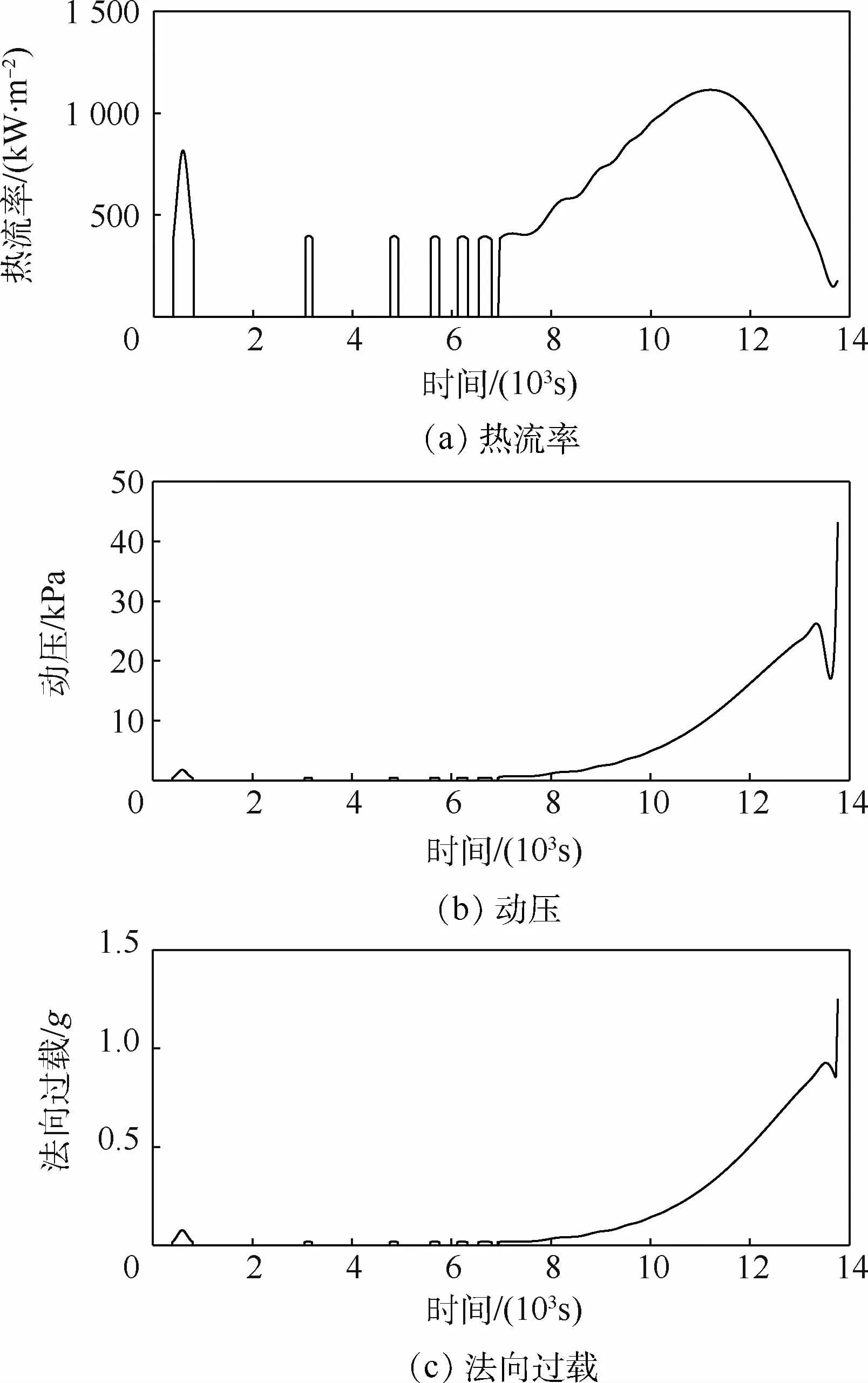
图7 过程约束随时间的变化Fig.7 Variations of process constraints changing with time

为方便分析，给出助推器2次点火分别消耗的燃料，以及再入过程中各个阶段的航程大小和飞行时间，如表1、表2所示。

表1 助推器点火消耗的燃料Table 1 Fuel consumed by booster ignition

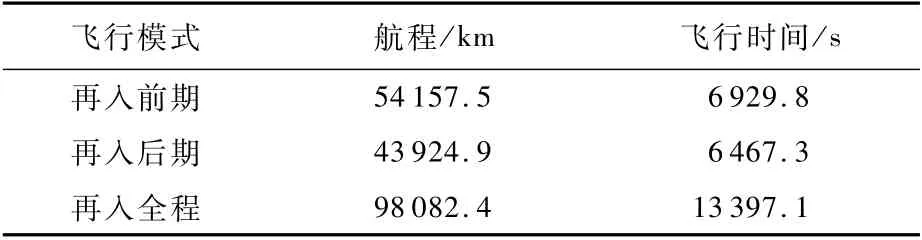
表2 动力增程型再入弹道的基本参数Table 2 Basic parameters of range-extended reentry trajectory

从仿真结果可以看出，再入前期的等高类周期跳跃弹道共点火2次，在第2次点火后，飞行器以合适的弹道倾角达到临界速度，顺利进入“打水漂”状态。直至速度减小至飞行器不再跳出大气层，进入再入后期的拟平衡滑翔段，最后以约束的高度和速度结束整个再入过程。最终，仿真得到的动力增程型高超声速飞行器再入弹道轨迹平滑，飞行器状态在整个再入过程中满足各项约束。

4.3 多种弹道形式的仿真对比

为证实本文提出的飞行模式具有高的燃料利用率、验证弹道解析解推导得出的结论，本节将等高类周期跳跃弹道（记为“弹道1”）分别与以下3种弹道作对比：“弹道2”为文献［12］中所提的周期跳跃弹道；“弹道3”为在波谷处点火的跳跃弹道；“弹道4”为文献［12］中提出的GPM 分段优化算法解算出的弹道，选取航程最远为性能指标，需预设σi与nb。各个弹道仿真条件相同，参数见3.1节。

图8为弹道1分别与弹道2～弹道4的高度、推力随时间变化的对比。助推器的启动方式为本文主要研究内容，因此以下针对助推器发生点火的再入前期弹道进行对比。图8中，弹道1与弹道4明显呈现类周期跳跃，而弹道2与弹道3呈现相位周期跳跃。

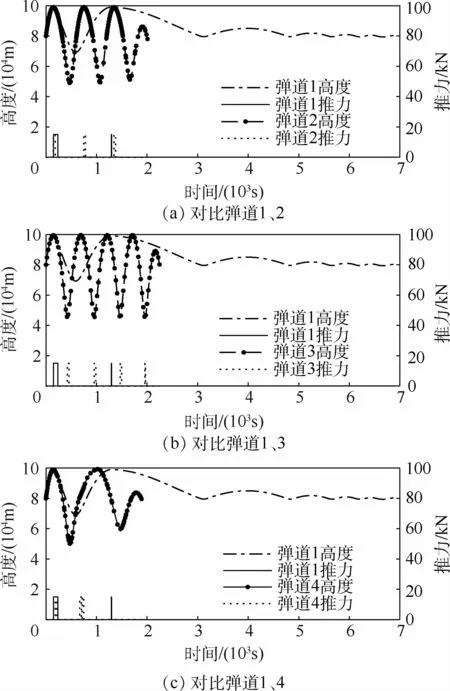
图8 不同飞行模式下高度、推力随时间变化的对比Fig.8 Comparison of variations of altitude and thrust changing with time under different flight modes

同样地，给出各个弹道的点火次数和每次点火消耗的燃料质量，以及航程大小、再入前期的末端速度和飞行时间对比如表3、表4所示。

表3 不同飞行模式下助推器点火消耗的燃料对比Table 3 Comparison of fuel consumed by booster ignition under different flight modes

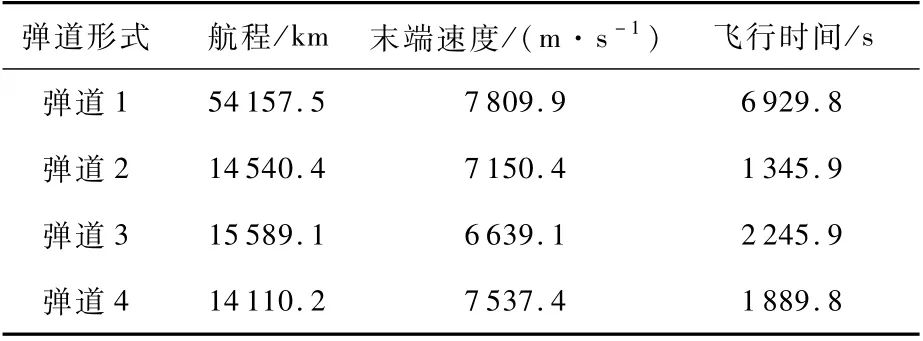
表4 不同飞行模式下弹道参数对比Table 4 Comparison of trajectory parameters under different flight modes

下面分别从燃料消耗、航程大小以及能量损耗3个方面进行分析。

1）燃料消耗：结合图8、表3数据可知，弹道1共点火2次，燃料消耗主要在第1次点火；弹道2、弹道3以及弹道4的前3次点火，燃料消耗量基本相同。弹道1的燃料消耗量以及点火次数均最少，总燃料消耗量约为其他弹道的95%。

2）航程大小：表4中数据显示，弹道1的类周期弹道航程明显大于其他弹道，约为其他弹道的3.47～3.84倍。

3）能量损耗：再入前期结束时，各个弹道高度相同、质量接近（燃料剩余量不同），可以忽略势能变化的差异，仅考虑动能。由表4可知，弹道1的末端动能大于其他弹道，约为其他弹道的1.04～1.18倍；弹道3具有最大的能量损耗。

所有弹道形式中，弹道1使用的助推器启动方式，最大限度地将助推器点火补充的能量转化为飞行航程以及飞行器机械能（体现在末端速度中）；而其余弹道形式为了获得航程，在消耗助推器能量的同时，还损失了飞行器本身的机械能。为了衡量各个弹道的燃料利用能力，本文提出式（26）来计算各个弹道的燃料利用率ηc，弹道编号c=1，2，3，4。

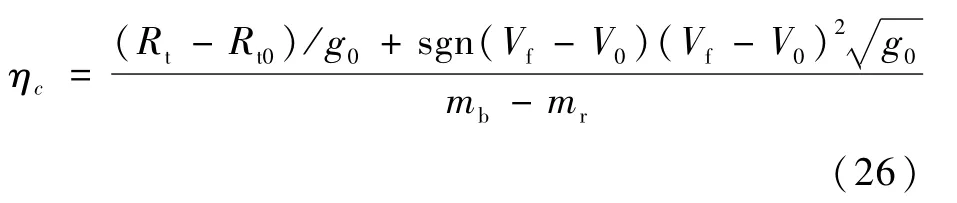
式中：Rt0=4782.6 km为助推器不点火时的航程；mr为助推器燃料剩余质量；sgn（）为符号函数。

结合表4数据，将计算结果归一化后分别为：η1=0.699 7，η2=0.099 4，η3=0.044 3，η4=0.156 6。可见，弹道1的燃料利用率最高，在式（26）定义下，为其余弹道的4.47～15.79倍；同时，2个类周期弹道的ηc值均高于周期弹道，弹道3值最小。

综上，本文提出的动力增程型弹道再入模式无论从燃料消耗、航程大小、能量损耗以及燃料利用方面均优于其他弹道，并且优势是十分显著的。因此，该飞行模式是相对于其余弹道形式更优的选择，该模式下的助推器燃料利用率与航程都是在文献［12-13］基础上取得了很大的进步。

5 结 论

1）本文设计了一种针对增强型高超声速飞行器的动力增程型再入弹道，该弹道再入前期通过设计助推器点火方式形成等高类周期弹道保证了航程最优，再入后期看作无动力返回的非线性轨迹优化问题以满足各项约束条件。

2）从再入弹道的解析解出发，得出了Sanger弹道达到航程最大的条件；进而提出再入前期轨迹规划策略；最终给出形成等高类周期跳跃弹道的动力装置启动方式的解，解决了“高度受限”以及“末端落点精度高”条件下，“点火次数”、“点火时机”和“点火时长”的计算问题。

3）再入后期提出以各项性能指标的加权和作为GPM算法的总性能指标，在航程足够远的同时，保证了优化轨迹的平滑程度，通过优化算法求解的弹道符合各项约束条件。

4）综合考虑每单位质量的燃料燃烧对增程和转化为飞行器机械能的贡献；相应地提出评判标准的数学表达式。

5）相对于现有研究成果、不同点火时机形成的弹道以及优化算法迭代的结果，本文提出的动力增程型再入弹道能够以95% 的燃料获得3.47～3.84倍的航程和1.04～1.18倍的末端动能，燃料利用率高达4.47～15.79倍。

6）从弹道跳跃方式上重新分析数据，可知，无论形成方式为何，相对于周期跳跃的规则弹道，类周期跳跃的弹道总是能够更好地将助推器点火产生的能量转化为机械能储存在飞行器中，并获得更高的末端速度和燃料利用率。

7）在大气密度分层、弹道倾角合适并且燃料充足的条件下，仿真实现了“打水漂”弹道。事实上，这样的弹道仅仅是理想化弹道，因为实际的空气环境不可能存在一个曲面将大气层和真空环境严格区分开。但是，这样的“打水漂”弹道作为一个标准，为实际工程提供了努力的方向。