基于修正IMM 的风机变桨系统故障诊断方法

王进花，朱恩昌，曹洁，余萍，3

（1.兰州理工大学 电气工程与信息工程学院，兰州730050； 2.甘肃省工业过程先进控制重点实验室，兰州730050；3.兰州理工大学 电气与控制工程国家级实验教学示范中心，兰州730050）

风能的开发和利用近些年正处于一个快速上升阶段［1］。风力发电机是风能转换电能的重要设备，其中的变桨子系统在维持风机的功率输出稳定和运行安全上起着重要的作用。

相对于发电机、齿轮箱等其他子系统，变桨系统故障诊断方法的研究起步较晚，但近几年国内外学者相继做出了许多尝试。文献［2］采用多胞形未知输入观测器解耦干扰，利用其生成残差检测变桨执行器卡死故障。文献［3］引入了一个故障指示因子来表征变桨执行器参数故障的缓变程度，并设计自适应观测器来估计指示因子。文献［4］使用变遗忘因子递推最小二乘算法对变桨执行器故障参数进行辨识实现诊断。文献［5］设计激励信号通过频域分析检测并隔离了早期执行器缓变故障。文献［6］设计观测器，并设计检测阈值，实现了变桨传感器缓变故障的检测。文献［7］设计多新息观测器与实际系统生成残差，实现了变桨传感器的恒增益和卡死故障的故障检测。上述文献对执行器缓变故障、卡死故障和部分传感器故障进行了初步的故障诊断研究，但对于变桨系统传感器的多故障的检测和分离问题的研究目前还很少。文献［8］验证了多模型自适应估计（MMAE）与扩展卡尔曼滤波（EKF）结合方法对电动变桨系统的不同传感器故障检测和分离的有效性，但其故障诊断准确度还有待进一步提升。

动态系统的故障诊断问题可抽象成一个混杂系统的估计问题［9］，即通过连续的系统输入输出来估计出系统当前的离散的工作模式或故障模式。本文变桨系统的传感器多故障诊断问题正是基于这种思路，建立不同的传感器故障模型并通过自适应估计来识别这些模型。交互式多模型（IMM）是一种经典的混杂系统状态估计方法，建立适当的模型集，集成多个滤波器进行状态估计［10］。通过模型概率的计算获得当前与实际系统最匹配的模型，IMM 可以完成多故障的检测与隔离，并能同时进行系统状态的估计。由于加入了交互环节，相较于MMAE等一般多模型方法，IMM方法有更好的模型识别能力和状态估计精度，得到了广泛的应用。文献［11］将改进的平滑变结构滤波器与IMM 结合对一类航天器的执行器参数故障实现了分离。文献［12］利用异步传感器融合改进IMM 结合卡尔曼滤波方法（IMMKF）完成了高速列车的牵引逆变器多个绝缘栅双极型晶体管（IGBT）开关管的开路故障的故障检测和多故障定位分离。但是没有考虑到IMM 本身的模型转移概率对故障诊断性能的影响。文献［13］采用IMM-KF对车辆垂向减振器不同程度的参数故障实现了分离，并分析了不精确模型转移概率会降低故障诊断结果的精度，但是并没有提出有效的解决方法。文献［14］采用模型概率变化的后验信息设计修正函数来在线修正IMM的模型转移概率。文献［15］则采用模型似然函数值进行模型转移概率矩阵的修正函数设计，同时保持主对角元素占优，一定程度上缓解了过度修正导致的模型切换速度下降。但是由于模型概率由模型转移概率进行引导，系统模式的切换是一种软切换，会导致一定的诊断延迟和诊断错误。

针对IMM故障诊断中固定模型转移概率导致的诊断准确性、速度下降和估计精度损失问题，本文引入粒子滤波（PF）方法和IMM 方法对包含传感器多种故障的风机变桨系统进行故障诊断和自适应估计；在非模式切换阶段对IMM的模型转移概率进行自适应修正，提高方法的状态估计精度；在模式切换阶段使用反转策略修正模型概率，以提高诊断速度和减少模型失配，进而提高诊断的准确性。

1 系统描述

本文研究中采用Odgaard等提出的4.8 MW风机基准模型［16］，其中各子系统之间的关系如图1所示，图中：β和βr分别为桨距角和其参考值；ωr和ωg分别为转子和发电机的转速；τg、τr和τgr分别为发电机转矩、转子转矩和发电机转矩参考值；Pr和Pg分别为发电机输出功率参考值和实际值；Vw为风速。风电机组系统由控制器、变桨系统、空气动力学系统、传动系统、发电机与变换器几部分组成。

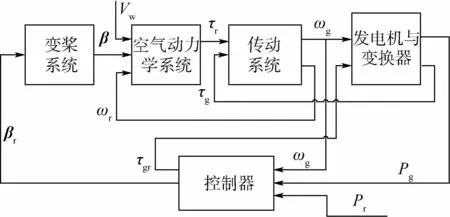
图1 基准模型子系统原理图Fig.1 Schematic diagram of benchmark model subsystem

变桨系统由3个独立控制的液压伺服执行机构组成，控制器分别对3个液压伺服执行机构提供电流信号来进行叶片桨距角的控制，以在高风速的工况下维持发电机的额定转速和恒定功率输出。其中一个独立的变桨执行器被建模成一个二阶动态系统：

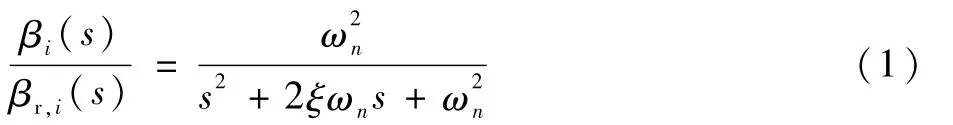
式中：βi（s）和βr，i（s）分别为第i个叶片的桨距角和其参考值；ξ为阻尼系数；ωn为自然频率。

将式（1）转化为状态空间方程形式，利用欧拉法进行离散化，并加入过程噪声、量测噪声和传感器故障得到式（2）所示的离散状态空间方程：

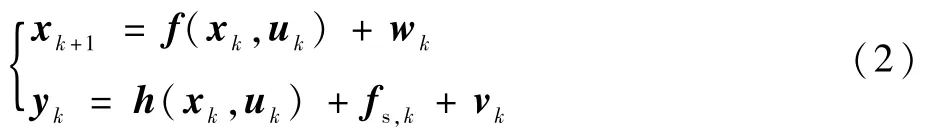
式中：xk、uk、wk、yk和vk分别为状态变量、输入变量、过程噪声、输出变量和量测噪声；fs，k为k时刻的故障模型；f（·）和h（·）分别为系统动态方程和观测方程。变桨系统由于频繁的动作和恶劣的工况，会因为一些机械、电气或环境因素导致传感器故障［8］，传感器故障主要可分为恒增益、恒偏差、卡死等故障。为了模拟发生某个传感器故障，需建立相应数学模型并于特定时间在仿真系统中注入这些故障。表1列出了4种传感器故障模型。

表1 传感器故障模型Table 1 Sensor failure models

2 基于修正IMM-PF的故障诊断

根据式（2）和表1所建立的变桨系统和M1～M4故障模型可以建立相应的滤波器，通过交互使各滤波器之间共享历史信息，各滤波器并行估计并根据似然函数更新各模型的概率，最后利用模型概率进行状态的融合输出和模型的识别，即完成状态估计和故障诊断。IMM 集成多个子滤波器来获得系统的状态估计，其中滤波器一般根据实际系统的情况进行选择。对于变桨系统，由于建模误差、风速扰动和噪声的复杂性，其模型的过程噪声通常呈现为非高斯分布［17］，因此本文采用PF作为IMM中的次优滤波器。

2.1 IMM-PF故障诊断方法

基于IMM的故障诊断方法，每个迭代周期内主要包含4个步骤。

步骤1输入交互。

IMM与PF结合时，交互和融合有多种方式，分别为模型层面的交互融合、粒子层面的交互融合以及粒子层面的交互和模型层面的融合。文献［18］对以上3种IMM 与PF结合方式进行了实验，结果显示第1种方式的目标跟踪性能最优，因此本文采用了此种方式。

输入交互就是在迭代周期的开始对各滤波器上一时刻的输出进行交互得到当前时刻的输入进行迭代，交互过程由式（3）～式（7）定义。

步骤2并行滤波。

式中：rand为随机函数。

根据建议分布进行重要性采样得到粒子的预测值：

根据观测值计算残差，用残差计算粒子权值，并归一化。

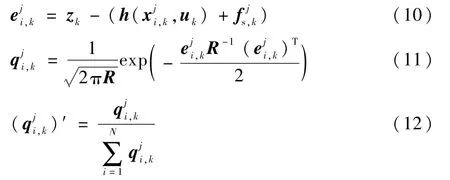
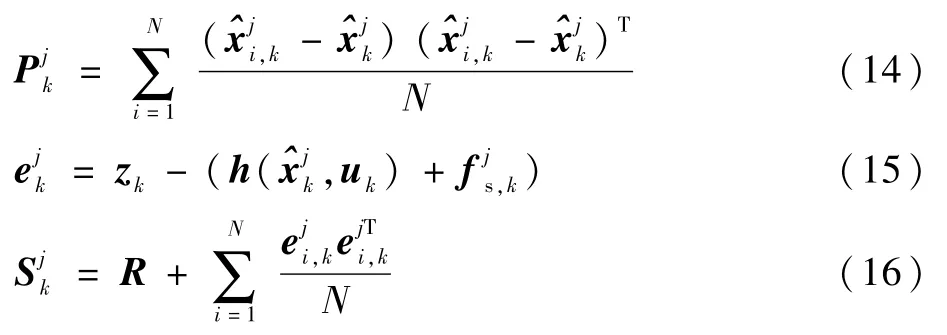
步骤3概率更新。

IMM利用每个滤波器估计值的似然函数根据式（17）来更新模型概率：

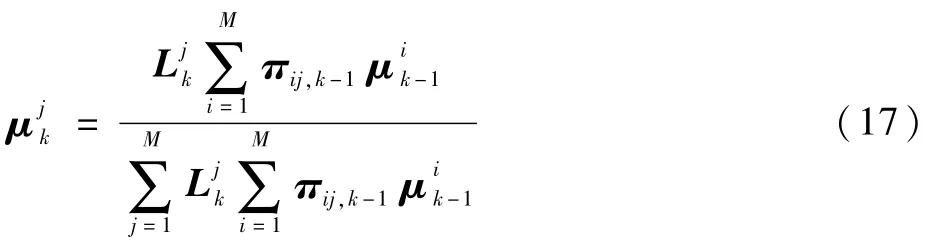
在正常工作模式下，正常模型对应的滤波器的模型概率应该逼近于1，当发生故障时，也就是发生模型切换时，相应滤波器的模型概率应该快速地上升到1，而其他的模型概率下降到0。将各滤波器的输出按式（19）～式（21）进行计算，根据模型概率进行加权融合得到IMM-PF的估计结果。

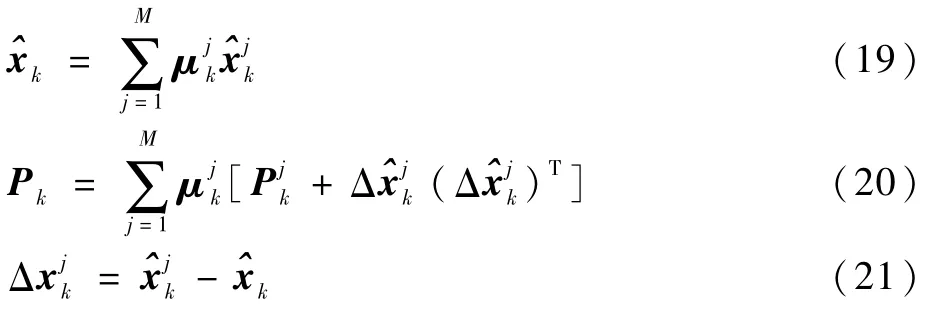
步骤4故障诊断。

利用式（17）计算得到的模型概率和式（22）、式（23）决策函数实现故障诊断。当模式失配时，模型集中没有与当前系统状态匹配的模型，会导致漏诊。

式中：μ′T为根据经验预先设定的诊断阈值，阈值小则诊断延迟小，误诊率较高，阈值大则诊断延迟大，误诊率较低。

IMM相较于其他方法有几个显著的优势：①由于同时用几个模型来表示系统的各个工作情况，相较于单模型的方法，IMM 在系统结构或参数发生变化时也能较好地完成状态估计。②单模型方法需要另外设计故障分离算法，而IMM可以同时完成故障检测和故障分离，方法设计和实施更容易。③因在每个迭代周期前后引入交互和融合步骤，相较于一般多模型方法，如MMAE，IMM的模型识别正确率更高，状态估计结果也更准确。

但IMM 故障诊断方法存在以下2个问题：①当系统处于非模式切换阶段时，由于标准IMM的模型转移概率矩阵是根据先验知识依经验预设的，并在整个方法迭代过程中保持不变，难以应对现实应用中的复杂变化。不精确的模型转移概率会影响滤波器之间的交互，并最终降低系统状态的融合估计精度。②系统处于模式切换阶段时，模式瞬间发生切换，IMM 通过计算出的模型概率来呈现系统模式的变化，匹配模型的概率超过阈值，则完成了对系统模式切换的跟踪。而模型概率的计算由模型转移概率引导，是一种软切换机制，所以存在一定的诊断延迟。而在这段延迟内会存在模型竞争，导致误诊和漏诊，同时也会降低状态估计的精度。

2.2 模型转移概率自适应修正

针对以上2个问题，本文提出了模型转移概率自适应修正策略和模型概率反转策略。IMM假设混杂系统的离散模式的随机跳变过程为一阶马尔可夫链，即模型之间的切换服从：

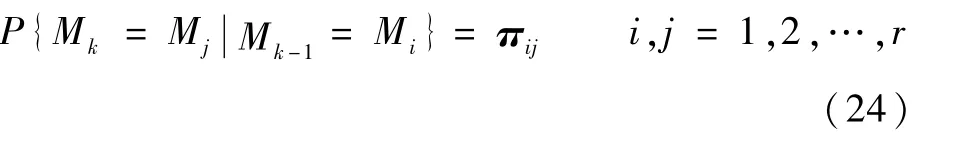
式中：Mk-1和Mk分别为当前和前一时刻的系统模型；πij为模型转移概率矩阵。模型转移概率表明了从上一个工作模式切换到另一个模式的概率，第i行的对角元素表示维持在上一时刻模式的概率，该行的非对角元素表示第i个模型向其他模型转移的概率，这种模式的依概率切换使得IMM利用较少的滤波器就可以获得较好的估计效果并能更好地捕捉系统的模式突变。

系统噪声会影响匹配模型的似然函数，并影响模型概率的占优程度，由式（17）可以看出，抑制这种影响，可以通过修正模型转移概率πij。在非模式切换阶段，对模型转移概率修正的主要目标是在系统模式稳定时保持匹配模型的模型概率占优。

IMM的后验信息模型概率反映了各模型与实际系统的匹配程度，它的变化也能很好地反应模型占优程度的变化，因此考虑利用其设计修正函数在线自适应地修正模型转移概率。

2.3 模型概率的反转策略

在模式切换阶段对模型概率修正的主要目标是保证模型概率在系统模式发生变化时快速地切换。IMM软切换机制会导致诊断延迟，而如果继续使用非模式切换阶段的修正策略，会使模型转移概率积累许多历史信息，即转移向某一模型的概率偏大，导致更长的诊断延迟。模型的似然函数也能反应模型与系统的匹配程度，且当模式发生变化时也会发生相应变化，因此采用模型的似然函数值之比λlik来切换修正方式，其计算公式为

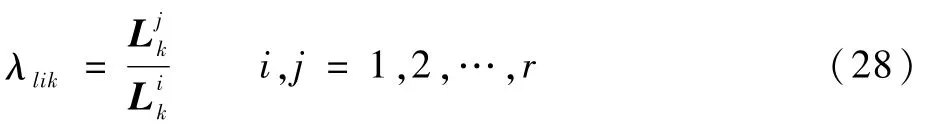
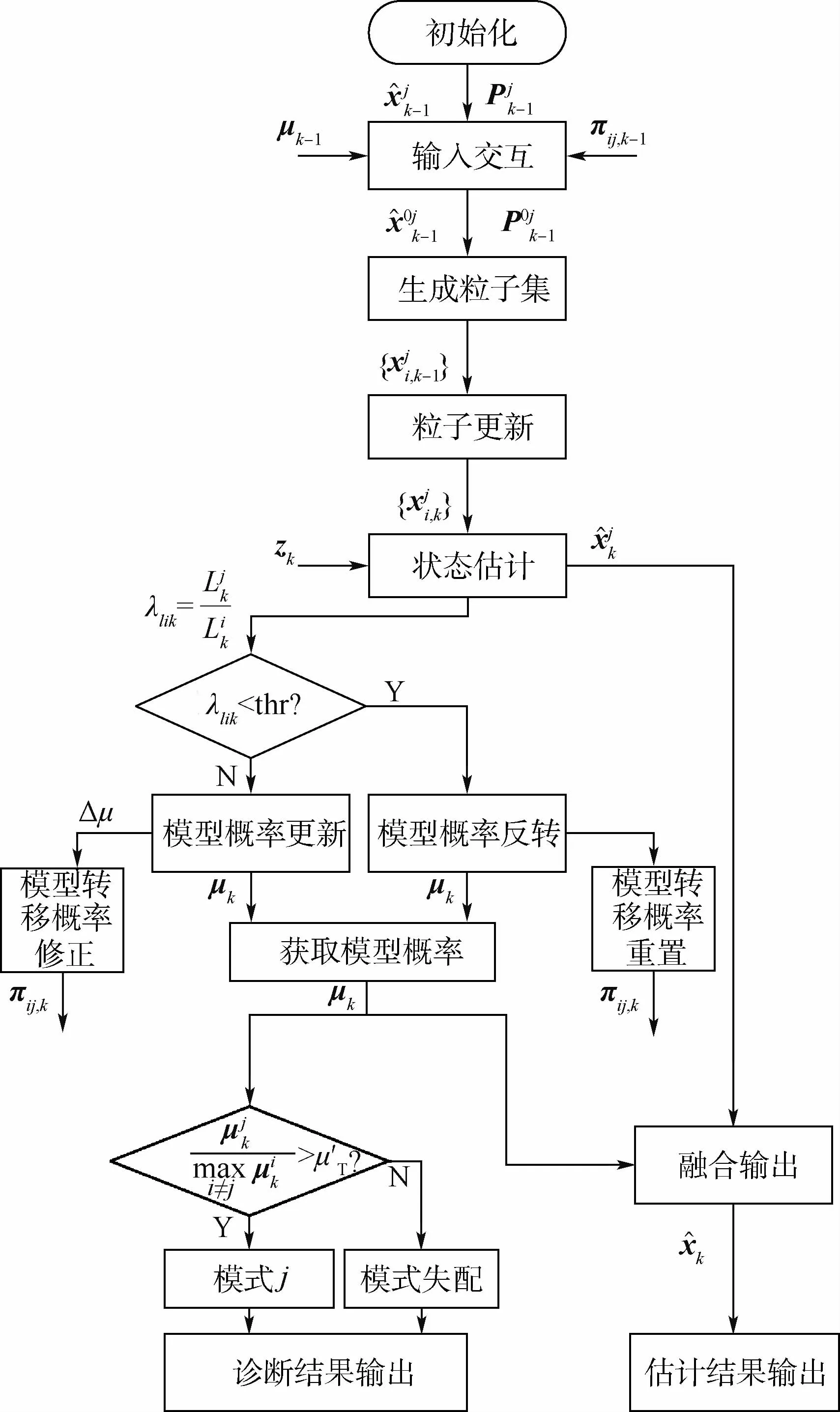
图2 MIMM-PF故障诊断方法流程图Fig.2 Flowchart of MIMM-PF fault diagnosis method

3 实验与分析

3.1 故障影响分析

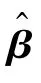
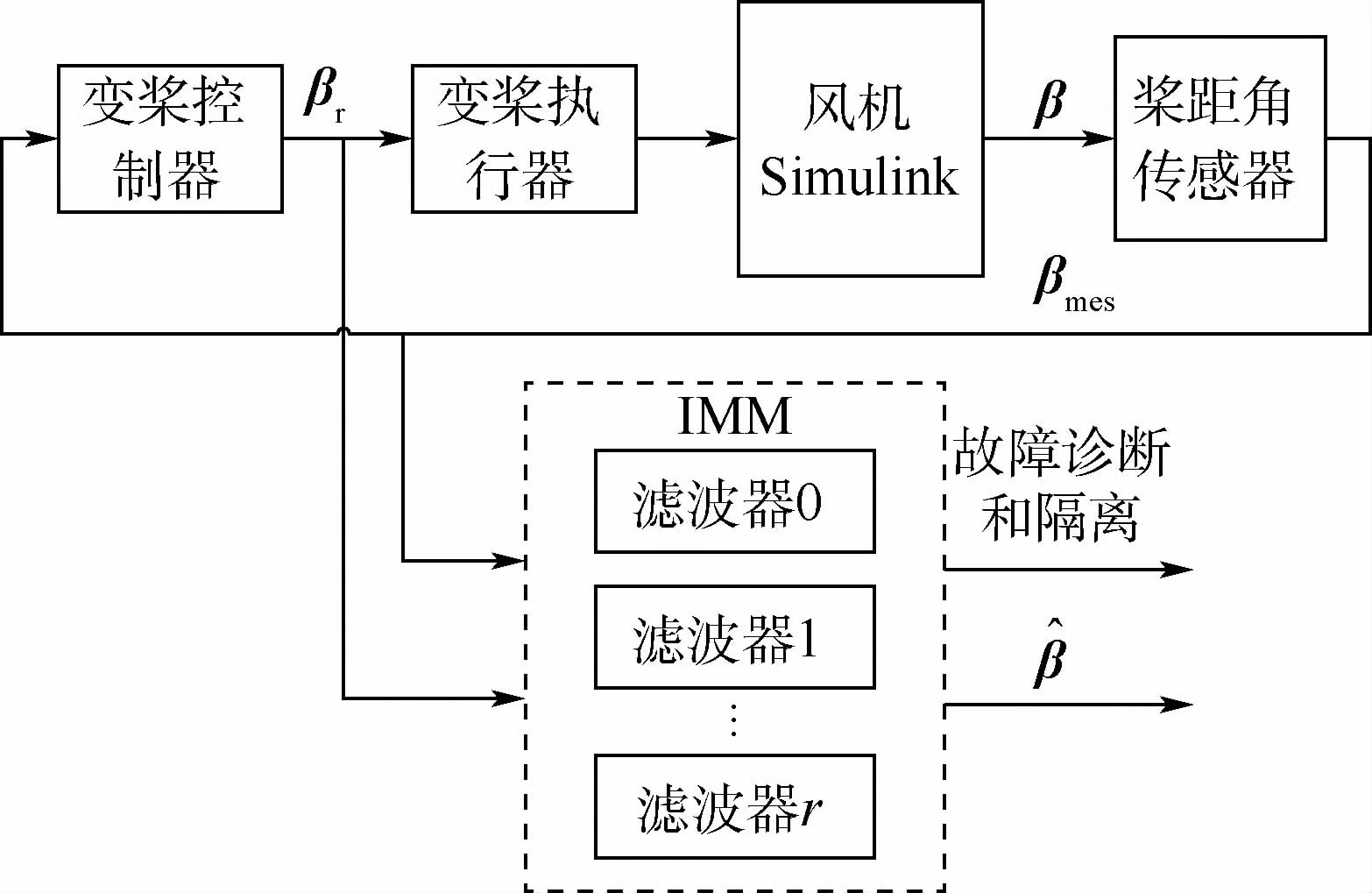
图3 仿真实验框架Fig.3 Framework of simulation experiment

所使用的风速覆盖了风机的2个工况：变速工况（风速3～15 m/s）和变桨工况（风速15～25 m/s）。由于变桨系统只有在高风速下的变桨工况才会进行变桨动作，本文选取变桨工况中的600个采样点进行仿真实验。选取3个传感器故障模型与正常模型构成模型集，其故障幅值与注入时间设置如式（29）所示：

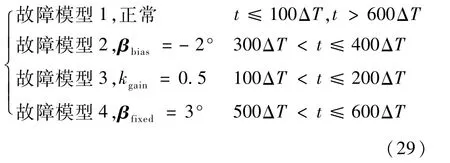
式中：ΔT为采样间隔。

通过如图4所示的正常叶片与故障叶片的仿真结果对比可以看到故障对变桨系统的影响。t在100ΔT～200ΔT范围内时，模式由正常到恒增益故障的切换瞬间故障叶片的传感器输出变为正常叶片的一半，而由于闭环系统中的PI控制器对故障具有补偿作用，变桨系统的输入值发生了反向的变化，导致桨距角也向相同的方向变化，从而传感器的输出慢慢变为实际桨距角的一半。t在200ΔT～300ΔT范围内时，模式由恒增益故障到正常的切换瞬间，由于前面传感器故障的影响，桨距角还处在反向异常的值，所以传感器输出有一个反向的跳变，随着故障消失，桨距角状态值和观测值也渐渐地恢复到和正常叶片一样。相同地，由于控制器的补偿作用，t在300ΔT～400ΔT范围内时，桨距角传感器发生-2°的偏置故障，t在500ΔT～600ΔT范围内时，发生卡死故障时，系统的输入和状态都发生了反相的变化。由于变桨系统传感器故障导致的这种复杂变化，传统基于单滤波器的故障诊断方法很难满足性能上的需求。

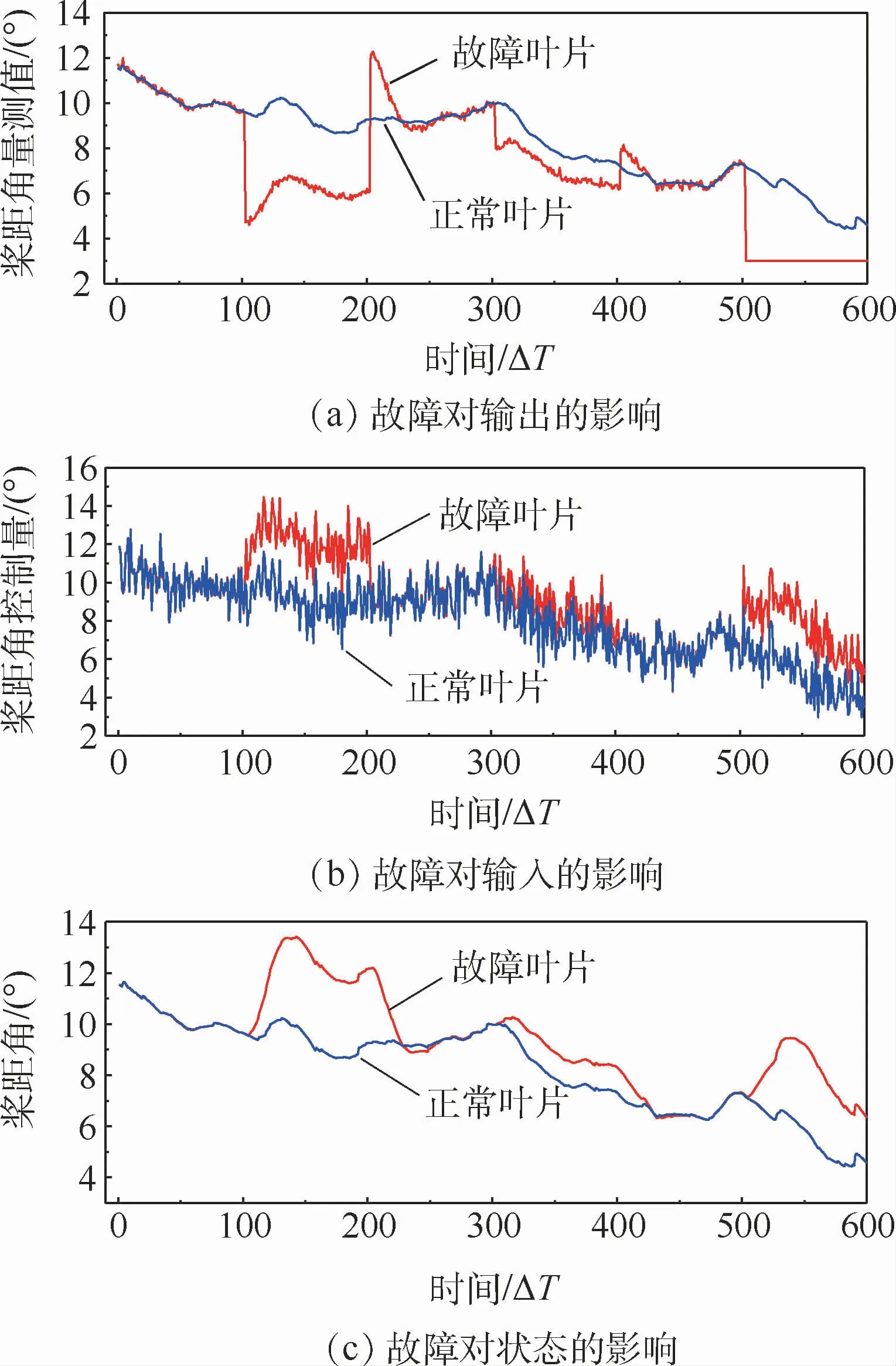
图4 故障对输出、输入和状态的影响Fig.4 Fault impact on output，input and state

3.2 方法验证

为了验证应用IMM-PF对风机变桨系统传感器多故障的有效性，针对式（29）所建立的模型集，分别设计4个相应的粒子滤波器，采用IMMPF故障诊断方法，对从图3所示仿真系统得到的输入输出数据进行在线的自适应估计，通过模型概率的计算得到当前时刻与实际系统最匹配的模型，并进行融合输出，从而得到变桨系统的状态估计和诊断结果，并与MMAE-PF进行了对比。实验参数设置如下：仿真时间为6 s，采样周期为0.01 s，粒子滤波器粒子数为50，过程噪声和量测噪声分别为w～Γ（0.1，0.1），v～N（0，0.001），桨距角初始值x0=10，诊断阈值μ′T设置为9.9，初始模型概率为μ0=（0.7，0.1，0.1，0.1）T，初始模型转移概率设置为

实验设备配置为Inter Core i5-8520@1.6 GHz，内存8 GB，操作系统Windows10。

使用标准IMM-PF故障诊断方法得到如图5所示的诊断和状态估计结果，图中模型序号为0表示识别结果与4种模型都不匹配的漏诊情况。从图5（a）可以看到，MMAE-PF方法出现了较多的漏报，而标准IMM-PF除了在模式发生切换时存在一定的时间延迟，整个过程有较少的漏报，诊断结果整体上与预设的模式序列相吻合。从图5（b）可以看出，MMAE-PF的估计偏离实际桨距角的程度较大，而IMM-PF大部分区间内的桨距角估计较为准确，误差较小，只是t在500ΔT～600ΔT范围内时，发生传感器卡死，桨距角估计都发生了振荡。这是由于输入值在变化，而滤波器无法获得相应的输出值的更新。从结果可以看出无论是故障诊断还是状态估计，IMM-PF总体上都可以满足需求。

图5 故障诊断结果和状态估计Fig.5 Fault diagnosis results and state estimation

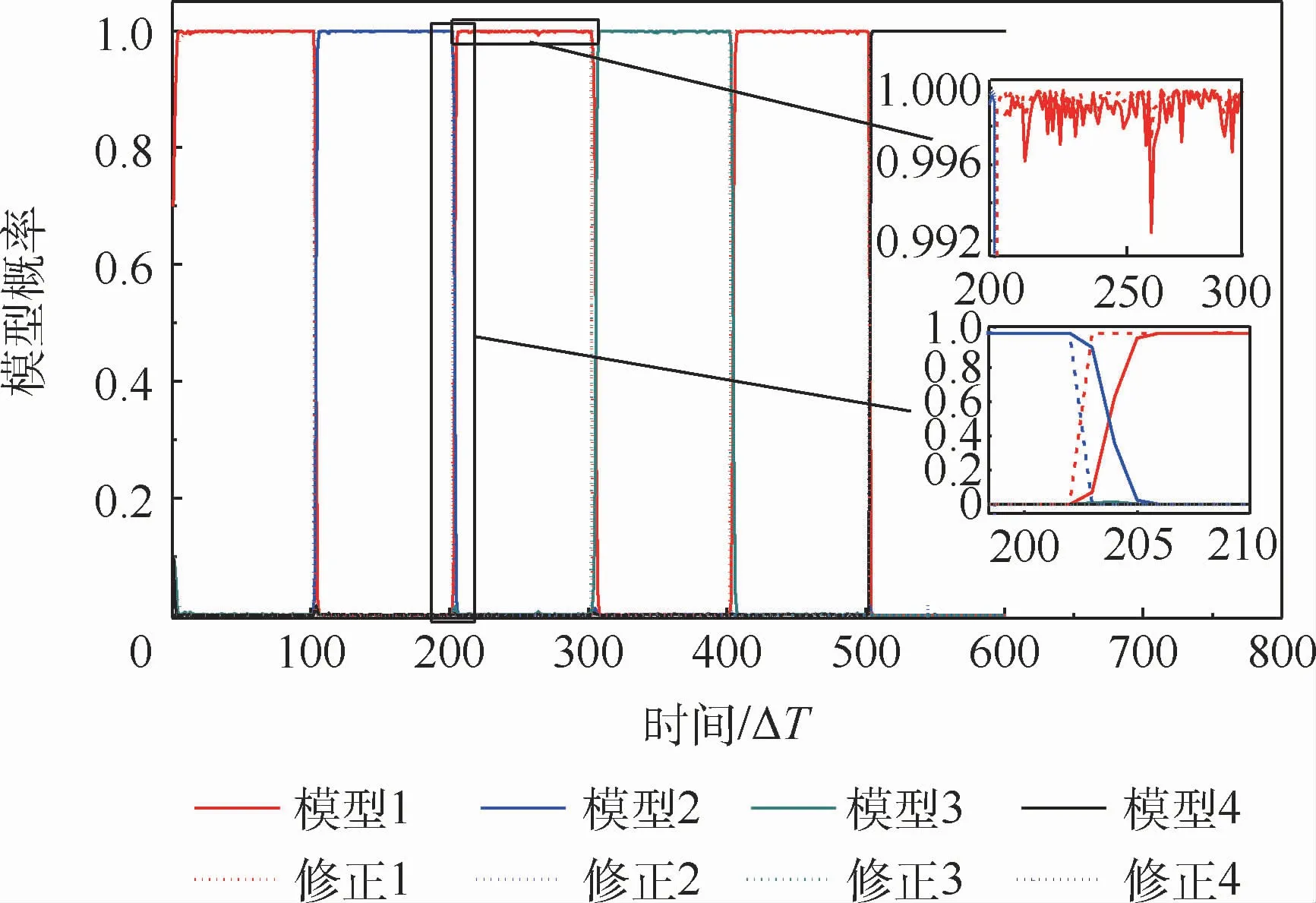
图6 模型概率变化曲线Fig.6 Model probability variation curves

为了验证所提出的自适应修正 IMM-PF（MIMM-PF）方法的性能，本文将其与标准IMMPF在3.1节所建立的故障诊断仿真框架下进行性能对比实验。方法修正前后的模型概率变化对比如图6所示，图中修正1～修正4为采用修正方法后的模型1、2、3、4的曲线。可以看到，在t=200ΔT处模型切换后的模型概率发生了反转，模型0的模型概率上升到接近1，其他模型的概率下降到接近0。而修正后相较标准IMM-PF方法的模型概率切换速度更快，切换后的模型概率也更接近于1。由于诊断和融合估计都要使用模型概率，这样的效果有利于提高方法诊断的速度、准确度和状态估计的精度。从图5（a）修正后的诊断结果可以看出，正确识别故障的数量明显增加，且在模型切换时的延迟和模型失配也得到了减少；从图5（b）的修正后的状态估计结果可以看出，桨距角也能更好地逼近真实值。

为综合评价这两种方法的性能，本文选取了以下3个指标：正确诊断（CDID），也就是诊断结果与实际模式匹配的个数，诊断延迟情况下从发生模式切换到给出正确诊断结果的时间间隔（Delay）以及融合估计的均方根误差（RMSE），其定义如下：

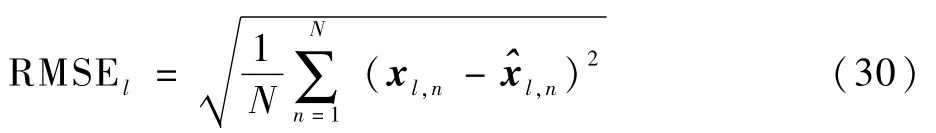
表2 MIMM-PF与标准IMM-PF性能对比Table 2 Performance comparison between MIMM-PF and standard IMM-PF

从表2中的数据可以看出，修正后的故障诊断方法提高了18.22个正确诊断数，提升了近3%，减少了2.676 7个采样间隔的延迟时间，降低了56.31%的估计误差。此统计结果表明本文所提出的修正方法对基于标准IMM-PF的故障诊断方法从准确性、速度和状态估计精度都得到了较好的提升。为进一步增加方法对于强噪声的鲁棒性，下一步的工作将对IMM-PF中的粒子滤波进行分析和改进，如文献［19］根据噪声和误差进行状态转移密度方差的自适应调整，以增加粒子滤波对强噪声的抗干扰能力。

4 结 论

1）建立了风机变桨系统传感器的多种故障的故障模型，将IMM与PF结合，在所建立的模型集上实现了自适应估计、故障检测与分离。

2）在此基础上，为IMM 方法设计了新的在线自适应修正方法。在非模型切换阶段，利用模型概率梯度设计修正函数自适应地修正模型转移概率。

3）利用模型似然函数比检测模式切换，并在模式切换阶段使用反转策略直接修正模型概率。

4）在风机仿真系统上应用所设计的MIMMPF故障诊断方法，可以实现预期的效果，并且诊断准确性、速度和状态估计精度相较标准方法都得到了较好的提高。