一类具有双参数的有序分数阶微分方程初值问题
张海燕,冯 冯
1.宿州学院数学与统计学院,安徽宿州,234000;2.灵璧县第五中学,安徽宿州,234000
本文考虑一类具有双参数的黎曼-刘维尔有序分数阶微分方程初值问题:
(1)
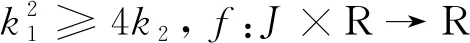
有序分数阶微分方程在自动化控制系统和非牛顿流体中有广泛的应用背景,近年来该领域获得了许多优秀成果[1-8]。特别地,文献[1-4]利用Banach压缩映射原理和Leary-Schauder不动点定理,获得了几类Caputo有序分数阶微分方程边值问题解的存在唯一性结论,参考文献[5-8]进一步给出了几类Hadamard有序分数阶微分方程边值问题的可解性。
上述文献均是对单参数情形下的有序分数阶微分方程问题进行研究,受此启发,本文考虑一类具有双参数的有序分数阶微分方程初值问题(1)。和已有文献相比,方程(1)中含有两个参数k1,k2,这会导致将分数阶微分方程初值问题等价变形为积分方程较有难度。本文通过分数阶积分算子,将问题(1)转化为常微分方程,结合相应的特征方程特征根方法和常数变易法克服上述困难。由于引入了双参数,问题(1)的研究更具一般性,应用范围更广泛,能更精确地描述一些控制过程模型。
1 预备知识
定义1[9]若可积函数g:(0,+)→R,则α阶黎曼-刘维尔分数阶积分定义为:
定义2若可积函数f:(0,+)→R,则α阶黎曼-刘维尔分数阶导数定义为:
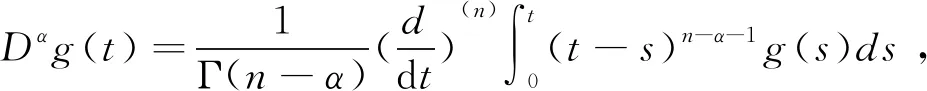
引理1若函数μ(x)在(0,1)上连续,且α>0,则分数阶微分方程Dαμ(x)=0的解为
μ(x)=c1xα-1+c2xα-2+…+cnxα-n
这里n如定义2所述,ci∈R,i=1,2,…,n。
引理2若函数g∈L(J,R)且p>q>0,则对任意t∈[0,1]有
IPIqg(t)=Ip+qg(t),DPIPg(t)=g(t),DqIpg(t)=Ip-qg(t)
引理3设k12≥4k2,x(t)∈C3(J,R)且g∈(J,R),则有序分数阶微分方程
(2)
有唯一解为
(3)
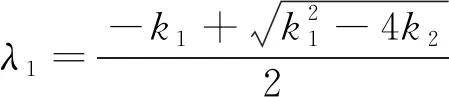
证明对方程(2)两边利用分数阶积分算子Iq直接积分,由引理1和引理2可得:
x(t)+a1tq-1+a2tq-2+a3tq-3+k1I1(x(t)+b1tq-2+b2tq-3)+k2I2(x(t)+c1tq-3)=Iqg(t)
其中a1,a2,a3,b1,b2,c1为任意常数。由初值条件x(0)=0可知a3=0。对上式求导数,有
x′(t)+a1(q-1)tq-2+a2(q-2)tq-3+k1(x(t)+b1tq-2+b2tq-3)+k2I1(x(t)+c1tq-3)=Iq-1g(t)
由初值条件x(0)=x′(0)=0,知a2=b2=0。接着对上式再求一阶导数,有
x″(t)+a1(q-1)(q-2)tq-3+k1[x′(t)+b1(q-2)tq-3]+k2(x(t)+c1tq-3)=Iq-2g(t)
由初值条件x(0)=x′(0)=x″(0)=0,知a1=b1=c1=0。因此有:
x″(t)+k1x′(t)+k2x(t)=Iq-2g(t)
(4)
此方程为二阶常系数非齐次微分方程,其通解为:
x(t)=yc(t)+yp(t)
(5)
其中yc(t)为方程(4)对应齐次方程的通解,yp(t)为方程(4)的一个特解。为求yc(t),考虑方程(4)对应齐次方程的特征方程ξ2+k1ξ+k2=0,其特征根为:
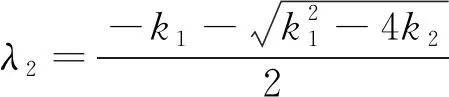
当k12>4k2时,λ1≠λ2,故方程(4)对应齐次方程的通解为:
yc(t)=d1eλ1t+d2eλ2t
(6)
其中d1,d2为任意常数。此时基础解系的Wronskian行列式为:
=(λ2-λ1)e(λ1+λ2)t≠0
结合(6)式,应用常数变易法,可得特解(7)式:
(7)
将(5)(6)(7)式代入(2)式,在初值条件下可知d1=d2=0,此时方程(2)的解为x(t)=yp(t)。
当k12=4k2时,λ1=λ2,方程(4)对应齐次方程的通解为:
yc(t)=e1eλ1t+e2teλ1t
(8)
其中e1,e2为任意常数。此时基础解系的Wronskian行列式为:
=e2λ1t≠0
结合(8)式,应用常数变易法,可得特解:
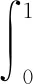
(9)
将(5)(8)(9)式代入(2)式,在初值条件下可知e1=e2=0,此时方程(2)的解为x(t)=yp(t)。
综上所述,(3)式成立,引理得证。
注1:若两参数值相同,方程(2)的解为x(t)=Iqg(t),这为常见情形,本文忽略。若k12<4k2,方程(4)对应齐次方程的特征方程有两共轭复根,处理方法和上文类似,本文不考虑此情况。

(10)
由引理3易知算子T在E中的不动点即为方程(1)的解。
引理4算子T:E→E是全连续的。
证明首先,由于f是连续的,因此算子T是连续的。接着,设Ω是E中的有界集,则由f的连续性知,对任意的x∈Ω,存在正数L>0,使得|f(t,x)|≤L,t∈J。因此有:

(11)
则算子T在Ω上是一致有界的。
然后,设t1,t2∈J且0≤t1 对∀ε>0,∃δ(ε)>0,当|t2-t1|<δ时,有: |eλ1(t2-t1)-1|<ε,|eλ2(t2-t1)-1|<ε, |eλ1t2-eλ1t1|<ε,|t2eλ1t2-t1eλ1t1|<ε 于是有: 因此,由等度连续的定义可知,算子T在Ω上是等度连续的。综上所述,应用Arzela-Ascoli定理可知T:E→E是全连续的,引理得证。 引理5[10]设D是巴拿赫空间E中的有界凸闭集,A:D→D全连续,则A在D中必有不动点。 引理6[11]设D是巴拿赫空间E的闭子集,F:D→D是一个严格的压缩映射,即对x,y∈D,|Fx-Fy| 为了方便,引入记号: 定理1若存在正常数A1,A2,对∀t∈J和x∈R,使得: |f(t,x(t))|≤A1|x(t)|θ+A2,0<θ<1 (12) 成立,则方程(1)在E中必有一解。 因此算子T:Dr→Dr,结合引理4可知T:Dr→Dr是全连续的。由引理5可知算子T在Dr中必有不动点,即方程(1)在E中必有一解。 定理2若存在正常数B1,B2,对∀t∈J和x∈R,使得: |f(t,x(t))|≤B1|x(t)|λ+B2,1<λ 证明与定理1证明相似,仅需Dr中r满足 定理3若存在正常数C1,C2,对∀t∈J和x∈R,使得: |f(t,x(t))|≤C1|x(t)|+C2, 成立且ΛC1<1, 则方程(1)在E中必有一解。 证明与定理1证明相似,省略。 注2:定理1-3对非线性项条件|f(t,x(t))|≤C1|x(t)|τ+C2,τ∈(0,+),分三种情况进行了讨论,获得了解的存在性充分条件。根据τ不同值,直接验证充分条件,得到相应结果,这在应用上是比较方便的。 定理4若存在正常数D1,对∀t∈J和x∈R,使得: |f(t,x(t))-f(t,y(t))|≤D1|x(t)-y(t)|成立且ΛD1<1,则方程(1)在E中必有一解。 先证明T:Dh→Dh。对x∈Dh,由(11)式和定理条件可知: 因此‖Tx‖≤Λ(D1‖x‖+D2)≤h,即T:Dh→Dh。 接着证明算子T是一个压缩映射。对x,y∈Dh,t∈[0,1],由定理条件可知: ≤ΛD1‖x-y‖ 因此,‖Tx-Ty‖≤ΛD1‖x-y‖,注意到ΛD1<1,因此算子T是一个压缩映射,由引理6可知T在E中存在唯一不动点,即方程(1)在E中存在唯一解,定理4得证。 例1考虑有序分数阶微分方程初值问题: (13) 结合定理1可知,此时A1=2,A2=1,θ=0.2,显然定理1条件满足,故初值问题(13)在E中必有一解。 例2考虑有序分数阶微分方程初值问题: (14) |f(t,x(t))-f(t,y(t))|≤0.5|x(t)-y(t)| 本文考虑了一类具有双参数的黎曼-刘维尔有序分数阶微分方程初值问题,通过利用常微分方程中的特征方程特征根方法和常数变易法,结合非线性分析中的Schauder不动点定理和Banach压缩映射原理,获得该问题解的存在唯一性充分条件,推广和改进了单参数情形下有序分数阶微分方程解的存在性结果。
2 主要结果
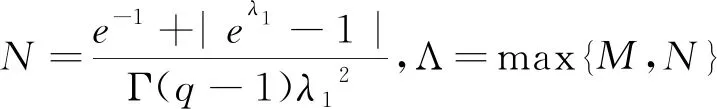
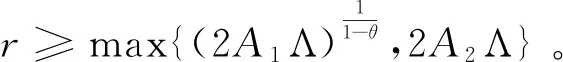

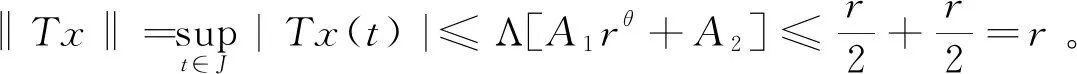
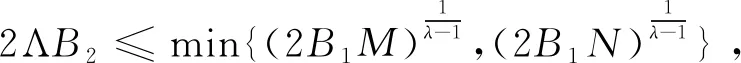

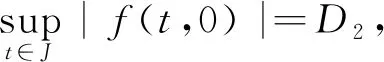
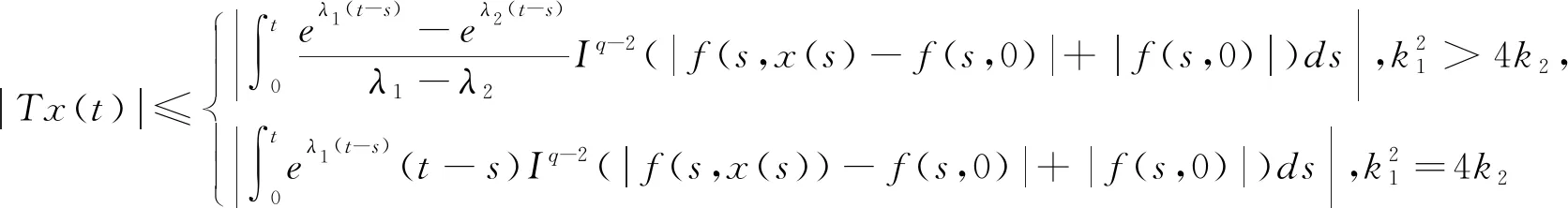
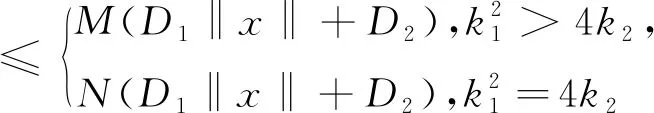
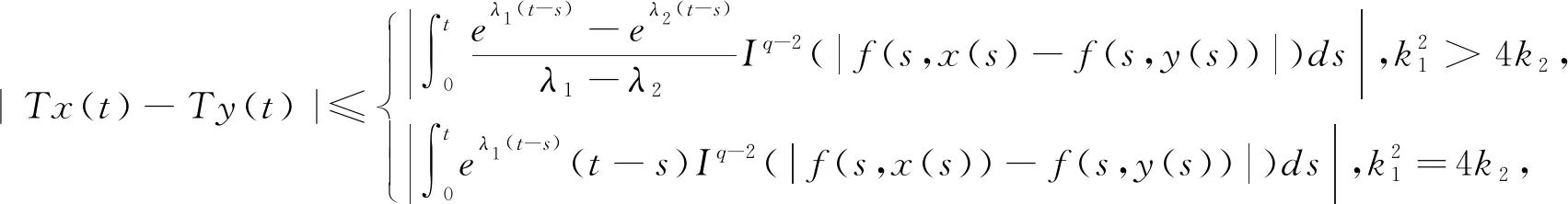
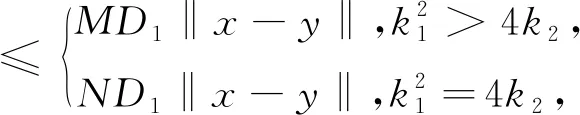
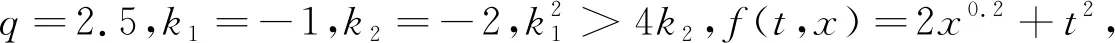
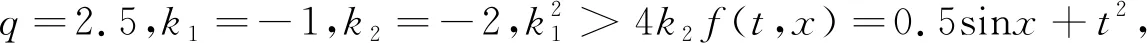
3 结 语

