巧用三角公式求数列通项
河北省邯郸市第一中学(056002) 白春林
近年来,随着大学招生模式的变更,强基计划的实施,很多尖子生都寄希望于通过自主招生获得一定的加分.纵观历年各校的自主招生试题可以发现,有关递推数列求通项的问题始终受到命题者的青睐.但是这部分题目往往难度较大,方法新颖,很多考生无从下手.下面就本人近年的教学实践,提供一类递推数列求通项的三角代换解法,希望对考生有所帮助.
例1数列{an}满足求a2020.
分析通过计算可得可发现数列{an}是一个周期数列,周期为6,所以a2020=a4=-2+
作为一个选择题,我们可以很快得到答案,但是数列的周期性与三角的周期性是否有关系呢? 通过下面的探究来解答.
探究把原式中分式部分上下同除以可得类比两角和的正切公式tan(α+β)=设an-1=tanα,则原式可以变形为an=又因为a0=所以
总结通过上面的解答过程可以发现,一个常见的周期性数列问题,其实是三角公式与数列的结合,通过对比研究,发现还有很多类似的题目,可以通过三角的公式与数列结合分析.
例2已知正数列{an}的前n项和Sn和通项an之间满足:则数列{an}的通项公式.
分析由Sn· an=作差变形可得2n-1an-1=类比正切的二倍角公式tan 2θ=设2nan=tanθn可得θn=从而求出an.
解析由原式可得:n≥2.作差得:
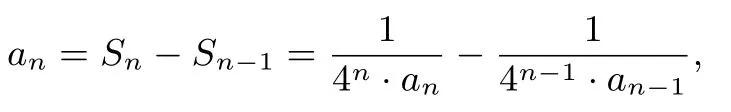
类比正切的二倍角公式tan 2θ=与上式有相似之处,所以把上式变形为:设2nan=tanθn,其中tan 2θn,所 以θn=因为a1=1,tanθ1=1,θ1==tanθn=
例3已知数列{an}满足an+1=a1=1,求an.
分析常规思路利用an+1=Sn+1-Sn带入原式无法求出通项,本题的巧妙之处是数列与余弦定理的相结合,把=+Sn+1 类比余弦定理a2=b2+c2-2bccosA,可以发现有相似之处,通过构造可得=+1-2Sn·1·在三角形中构造an+1与Sn的关系.
解析由an+1=可得an>0,Sn>0,把原式两边平方并化简可得=+Sn+1,即=+1-2Sn·1·构造一个三角形,三边分别是an+1,1,Sn,在三角形中设Sn和an+1的夹角为θn,考虑到Sn+1=Sn+an+1,可构造如下图形,上图中的三角形满足易得θn=2θn+1,因为θ1=π3,所以在图(1)的三角形中利用正弦定理可得所以
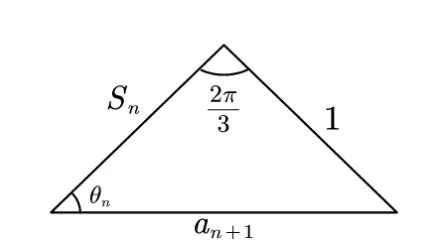
图(1)
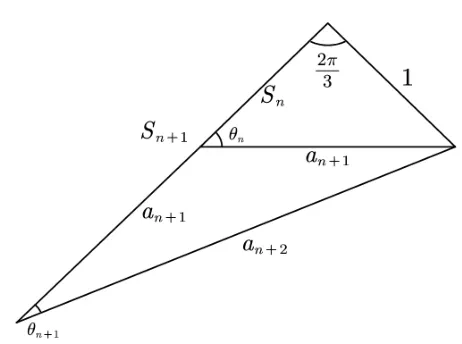
图(2)
三角函数的应用极为广泛,可以沟通不同的数学知识点,如三角与不等式,三角与函数,三角和解析几何,三角与数列等等,利用三角代换,常常可以突破难点,提供简单的解决方法.三角代换是一种典型、实用且简便的解题方法.
本文探讨如何依据三角函数公式,通过类比的方法求出有关递推数列的通项问题,涉及两角和的正切公式,正切的二倍角公式,余弦定理,正弦定理以及数列求通项公式的联合应用.数列是高中教材的重点和难点,而递推数列则是难点中的难点,多数为探求数列的性质.而且有许多问题可以借助三角公式进行代换从而得到巧解.

