一道解析几何试题的多种解法及结论推广
江苏省无锡市第一中学(214031) 冯一成 李 杨
笔者在进行一道解析几何问题的求解时尝试应用了解决此类问题的各种方法,并在解法中得到了启示,发现了一些漂亮的结论,分享给读者.
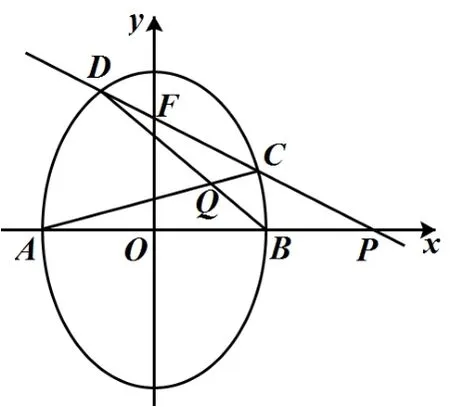
题目椭圆有两顶点A(-1,0),B(1,0),过其焦点F(0,1)的斜率为k的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
(1)略.(2) 当点P异于A,B两点时,求证:为定值.
一、解法赏析
解法一(设而不求,整体运算)由已知可得椭圆方程为设l的方程为y=kx+1,则点P的坐标为又
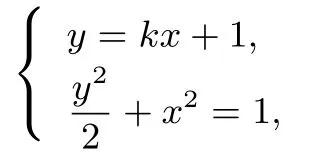
消去y可得(2+k2x2+2kx-1=0.设C(x1,y1),D(x2,y2).直线BD的方程为y=(x-1),直线AC的方程为y=(x+1),联立两条直线方程,可得点Q的横坐标为
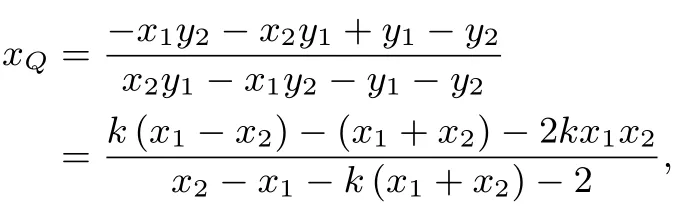
由韦达定理可知
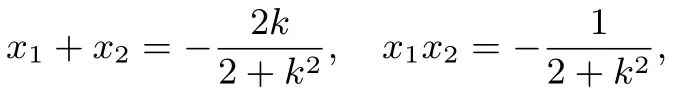
代入上式,可得
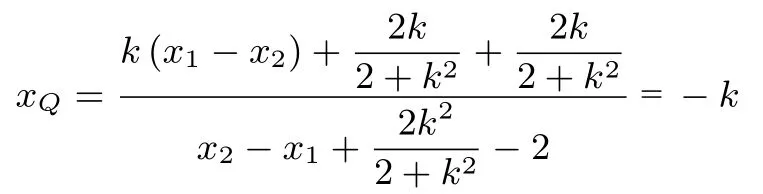
此法流畅自然,韦达定理的应用符合学生认知水平,关键步骤在于合理保留x1-x2部分不代换,通过整体运算,达到化简得目的.
解法二(设而求之,求点代入)同解法一解得
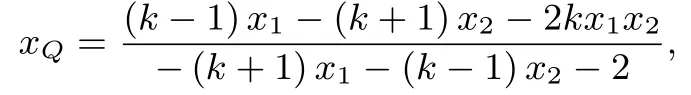
通过求根公式可以得到
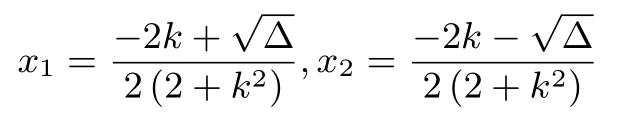
代入可得
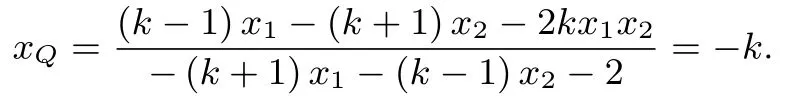
此法摆脱了解法一中对于式子化简时需要部分保留构造对称的要求,结合求根公式代入化简直截了当,但是对于判别式没有过早的代入,这是一个常用技巧,因为过早代入容易造成式子变得更为复杂影响运算的思路,同时适时的提公因式也让运算变得更为简单.
解法三(先猜后证,简化运算)假设点P和点B重合,此时点Q就是点P,所以可猜出的定值为1.以下来证明下式成立:
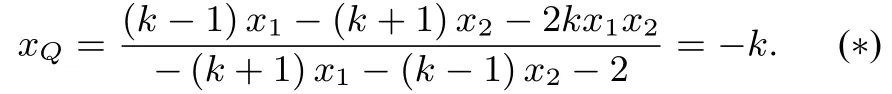
通过变形做差可得
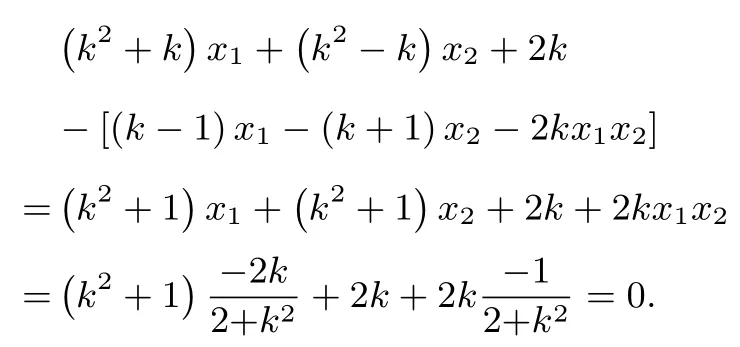
因此(*)成立,从而=xP xQ+yP yQ=1.
此法先猜后证,将探究题变成了证明题,目标变得更为直接,整个运算变的更为简单.
解法四(设点运算,局部化简) 设点C(x1,y1),D(x2,y2),然后求出直线方程
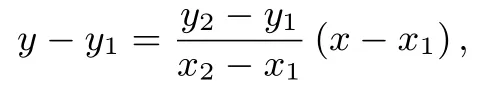
令y=0 解得又
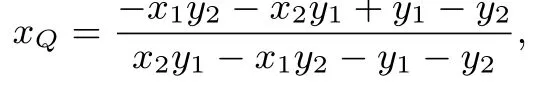
则
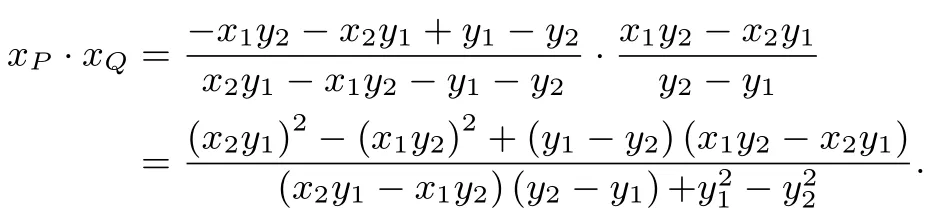
又C,D在椭圆上,所以代入可得
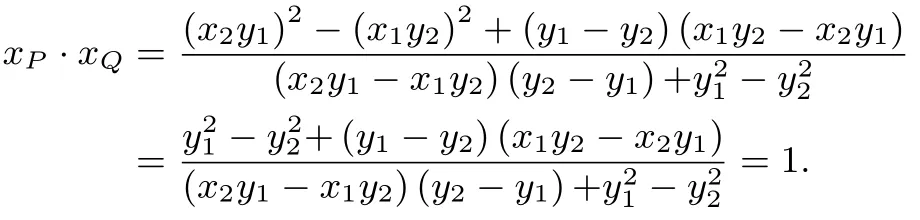
此法在运算过程难度最大,其中涉及四个变量,直至最后一步依然保留四个变量,但是利用局部化简的手段,最终得到了结果.解法四看似最为复杂,但给了笔者最大的启发,下面将思考的过程和探求的结论与读者一起分享.
二、结论推广
笔者发现在通过解法四的运算过程没有用到直线l通过点F这一条件,只要满足直线与椭圆相交即可,故此题应该有更为一般的结论.从位置上看此题中P,Q两点是椭圆的一条弦与短轴所在直线的交点,以及短轴两个端点与弦的两个端点的对应连线的交点,故可一般化为
结论一若椭圆方程为=1(a>b>0),A,B为短轴两端点,直线l与椭圆交于C、D两点,并与短轴所在直线交于点P,若直线AC与直线BD交于点Q,则
简证同解法四可解得
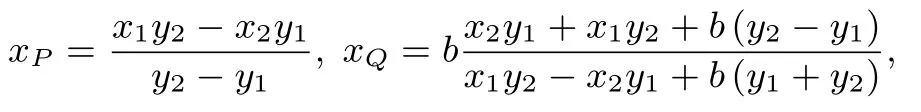
则
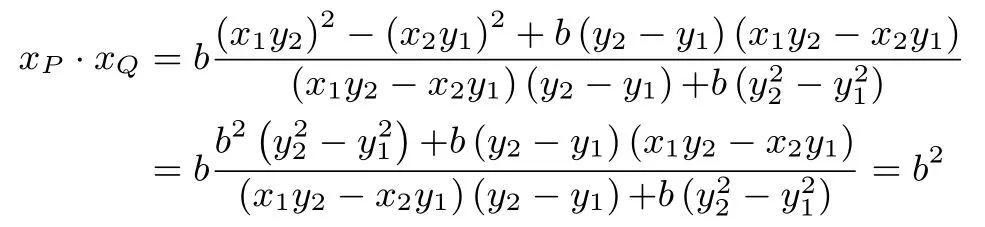
继续思考,若将P,Q两点变化为椭圆的一条弦与长轴所在直线的交点,以及长轴两个端点与弦的两个端点的对应连线的交点可得
结论二若椭圆方程为=1(a>b>0),A,B为长轴两端点,直线l与椭圆交于C、D两点,并与长轴所在直线交于点P,若直线AC与直线BD交于点Q,则
继续思考,在证明过程中(x1y2)2-(x2y1)2是运用了椭圆方程进行了消元得到了很好的对仗,那么,与椭圆拥有类似二元二次方程的圆与双曲线应该也有类似结论,于是进一步得到了
结论三圆O的半径为r,AB为其一条弦,若直线AB与过圆心的直线l交于点P,且圆与直线l交于C,D,若直线AC与直线BD交于点Q,则
结论四若双曲线方程为=1(a>0,b>0),A,B为实轴两端点,直线l与双曲线交于C、D两点,并与实轴所在直线交于点P,若直线AC与直线BD交于点Q,则
继续探索,若将上述结论中的弦的两个端点慢慢靠近,则弦就会退化为一个点,此时结论会发生一定的变化,因为点与轴就没有交点了,但是通过类比,笔者发现若弦退化为一个点,则只需将弦与轴的交点变为切线与轴的交点则结论依然成立,于是得到了
结论五圆O的半径为r,A为圆上一点,直线L过圆心O,若圆O在A处切线交直线L于P,则
结论六若A为椭圆=1(a>b>0)上一点,椭圆C在A处切线交长轴于P,交短轴所在直线于Q,则
结论七若A为双曲线=1(a>0,b>0)上一点,若椭圆C在A处切线交长轴所在直线于P,则
结论五,六,七无论从形式还是证明过程上都变得更简单,数学之美尽显.
三、结语
回顾问题的研究过程,笔者发现,若没有对此问多种解法的探求,以及对解法内涵的深入思考,就无法开启思维之门,当我们在思维之门开启后,你就会推开后面一扇又一扇探索之门.曾有人说:“当我们找到第一个竹笋时,你一定要再看看四周是否还有其它竹笋,因为它们往往结伴成长.”在研究数学问题时,道理是一样的.在大胆设想,小心求证的研究态度下,我们可以尝试通过联想,类比,抽象,概括等多种手段,将问题从特殊推广到一般,也许我们就能够发现更多数学中美丽的结论.

