基于气压高度辅助的机载自主完好性监测算法

陈维娜，杨 忠，顾姗姗，王逸之

（金陵科技学院，南京211169）

0 引言

随着卫星导航系统的应用,为了进一步提高空中交通系统的导航性能和安全性,国际民航组织提出了所需性能导航的概念［1-2］。该技术是利用飞机自身机载导航设备和全球定位系统（Global Positioning System,GPS）引导飞机起飞降落的新技术。由于具有全天候高精度测速、授时及定位能力,GPS目前已作为民航系统引导飞机进近着陆的主要导航系统。受到卫星星历、星钟误差、电离层和对流层延迟、多路径和接收机热噪声等因素的影响,机载卫星导航系统的定位误差可能会超出空域监视所容许的范围,即存在定位完好性问题［3］。

目前,常用的完好性监测算法可分为两类：内部监测算法和外部监测算法。外部监测算法是将卫星观测量误差源的误差修正值通过数据通信链广播给用户,对用户接收机的观测误差加以改正,以达到削弱这些误差源影响、改善用户定位精度的目的。受地面站之间以及地面站与卫星之间通信延迟等因素的影响,该算法信息更新周期相对较长［4］。内部监测算法包括接收机自主完好性监测（ReceiverAutonomousIntegrityMonitoring,RAIM）和机载自主完好性监测（Aircraft Autonomous Integrity Monitoring,AAIM）两类,RAIM利用卫星冗余信息对测量值进行一致性检验从而实现完好性监测,主要包括奇偶矢量法、最小二乘残差法、假设验证法、加权RAIM法等［5-8］,但RAIM依赖于可见卫星的几何分布,不能保证在整个时空均有足够的冗余信息来进行完好性监测［9］；AAIM借助飞机上的其它辅助信息（如气压高度表、惯导等）［10］,实现卫星的故障检测和故障识别,能有效提高卫星导航系统完好性监测能力。目前,AAIM的研究主要集中在基于惯性导航系统辅助的完好性增强算法上［11-13］,然而惯性导航系统的高度通道是发散的,在卫星导航系统垂直性能辅助监测上效果较小。气压高度表是飞行器不可或缺的仪表设备,能提供较高精度的高度信息,具有不依赖外界信息、隐蔽性好、抗辐射性强、全天候等优点［14］,利用气压高度表辅助卫星导航系统是一种较为理想的方案。

本文针对提高GPS完好性监测性能,提出了一种气压高度表辅助的机载自主完好性监测算法。利用气压高度表提供的高度信息建立了气压高度辅助完好性监测的系统观测方程,并推导了基于多解分离的完好性监测及完好性指标计算方法,从而实现对故障卫星的有效监测和识别。通过仿真,从可用性及故障检测能力等方面进行对比分析,表明该算法能有效提升卫星导航系统的完好性监测性能。

1 气压高度辅助下的组合系统模型建立

根据卫星导航系统及气压高度表的导航与定位原理,建立气压高度辅助卫星导航系统完好性监测的组合系统观测模型。假设有n颗可见卫星,每颗卫星的坐标分别为 （x1,y1,z1）、 （x2,y2,z2）、…、（xn,yn,zn）,机载卫星接收机的真实位置坐标为（x,y,z）, 其估计位置坐标为,则真实位置坐标与估计位置坐标之间的偏移量用（Δx,Δy,Δz）表示。卫星钟与接收机时钟的钟差估计值为,真实钟差与估计钟差之间的偏移量用ΔtGPS来表示。卫星到卫星接收机的伪距为ρi（i=1,2, …,n）, 可得出相对于估计位置的伪距

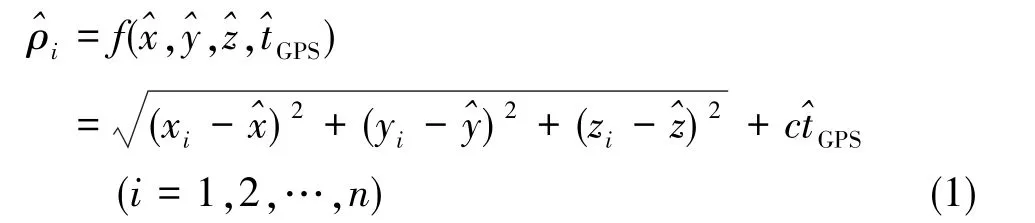
对式（1）进行Taylor级数展开,有

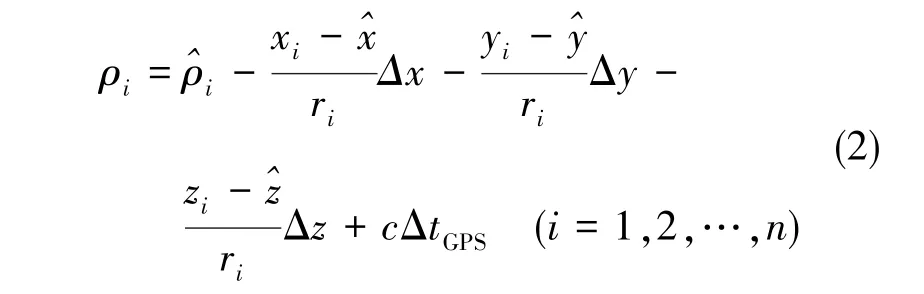
式（2）中,

因此,可建立卫星导航系统的观测方程

式（4）中,y为观测量,即卫星伪距与近似计算距离之间的差值；G为观测矩阵,aij（i=1,2,…,n,j=1,2,3）为观测矩阵系数；x为待估计状态量,由协议地球坐标系下的3个位置误差Δx、Δy、Δz以及接收机时钟误差ΔtGPS在内的4个状态量构成；ε为n×1阶矢量,为由于卫星选择可用性、接收机噪声及传播不确定性带来的量测噪声向量,其标准差为σGPS。 为了便于引入气压高度计的观测信息,将状态量投影至地理坐标系,其坐标转换公式如下

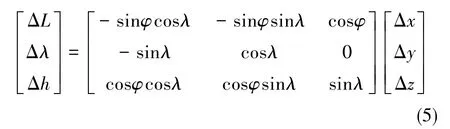
式（5）中,ΔL、 Δλ、 Δh分别为载体的纬度误差、经度误差和高度误差,λ、φ分别为载体的经度和纬度。

气压高度表利用气压表测量周围的大气压力,并根据气压与高度的关系,通过观测的气压计算得到载体飞行海拔高度,选取气压高度作为观测信息［15］, 得到观测方程如下

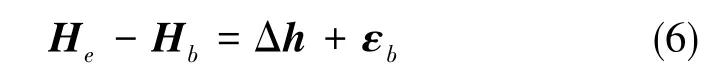
式（6）中,He为载体估计位置高度,Hb为气压高度,εb为气压高度计测量误差, 其标准差为σb。

综合式（4）和式（6）,可以得到气压高度计辅助卫星导航系统完好性监测的组合系统观测模型

式（7）中,Z为观测信息,包括卫星和气压高度表的观测量；H为观测矩阵；X为状态量,对应地理坐标系下的位置误差及卫星钟差等效距离误差；V为量测噪声矩阵,其均值为0,方差阵为；G′为n×4阶矩阵,为观测矩阵G经过式（5）坐标转换后得到的卫星导航系统观测矩阵。

2 基于多解分离的气压高度辅助完好性监测实现

在建立气压高度辅助完好性监测的组合系统观测模型基础上,采用多解分离方法实现卫星完好性监测。通过每次排除一个不同的观测信息,从而构成多个位置估计。利用所有量测信息获得的估计定义为主估计,排除一个观测信息后获得的估计定义为子估计,并根据不同估计之间的差值与设定门限进行判断比较,从而实现卫星的故障检测与隔离。

根据组合系统的观测方程,利用加权最小二乘估计原则,得到全观测条件下的状态主估计

式（8）中,W为正定加权矩阵,且W=R-1；S0为全观测条件下的最小二乘解矩阵,维数为4×（n+1）阶。同理,去除第i颗卫星观测伪距,利用其余观测信息进行状态求解,得到状态子估计

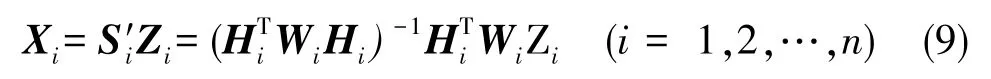
式（9）中,Zi为排除第i颗卫星伪距信息后的观测信息,Hi、Wi分别为与之对应的观测矩阵和加权矩阵；S′i为不完全观测条件下的最小二乘解矩阵,维数为4×n阶。为了便于后续的推导和计算, 将矩阵S′i进行重构扩充为4×（n+1）阶, 其对应第i列为零向量,得到新的矩阵Si, 即有

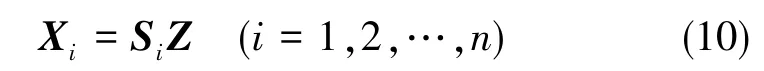
设状态量的真实估计为Xt,表示载体在地理坐标系下的位置修正量及卫星钟差等效距离误差,则由观测噪声给全观测估计和子估计带来的估计误差为

主估计与子估计之间差值协方差矩阵的定义和计算公式下

构建统计检验量di（i=1,2,…,n）

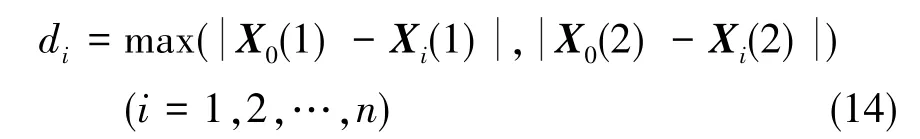
给定误警率Pfa,则对应每个子估计的统计检验量的检测门限Ti（i=1,2,…,n）为

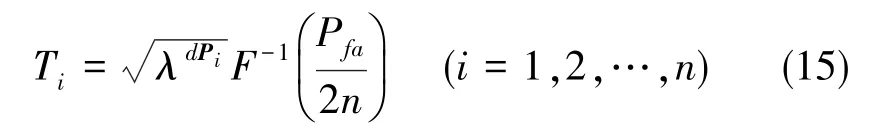
式（15）中,λdPi为对应dPi水平位置方向上的最大特征值, 可由dPi（1,1）、dPi（1,2）、dPi（2,2）计算得到；F-1为余误差函数的反函数,其表达式为

则根据n组检验量进行故障检测,其故障判据为：

1）无故障H0：所有检验量均满足di≤Ti；

2）有故障H1：至少存在1组检验量为di＞Ti。

多解分离法的层次架构图如图1所示。

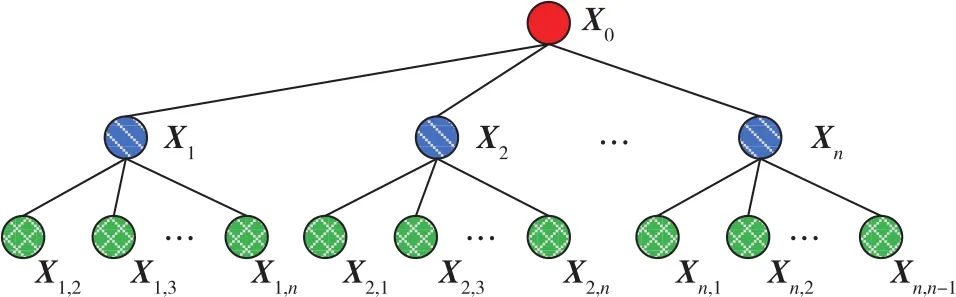
图1 多解分离法层次架构图Fig.1 Hierarchy of multiple solution separation

图1中,X0为全观测条件下的状态主估计,Xi（i=1,2,…,n）为去除第i颗卫星观测伪距下的状态子估计,Xi,j（i=1,2, …,n,j=1,2,…,n,且j≠i）为去除第i颗和第j颗卫星观测伪距下的状态子子估计。故障检测与识别流程如下：

1）若主估计X0与子估计Xi（i=1,2, …,n）构造的检验量均小于设定门限,则无故障；若存在1组检验量大于设定门限,则表明有故障卫星。

2）在检测出有故障后,对于故障定位识别,需要子估计及其次级估计（即在子估计观测信息中再排除一个卫星观测）。采用上述相同方法计算子估计Xi（i=1,2, …,n）与子子估计Xi,j（i=1,2,…,n,j=1,2,…,n,且j≠i）的统计检验量,若存在1个子估计Xk（k=1,2,…,n）及其对应的子子估计Xk,j（j=1,2,…,n,k=1,2,…,n,且j≠k）构造的统计检验量均小于检测门限,则可判定第k颗星故障；若所有子估计及其对应的子子估计之间构造统计检验量均存在大于门限的情况,则表明存在多星故障。

3）按照上一步过程进行类推,在排除两个卫星伪距观测量的基础上,计算子子估计及其次级估计之间的统计检验量,并根据故障判据进行故障识别。

结合航空飞行器的所需导航性能（Required Navigation Performance,RNP）技术需求,对载体的水平保护级别（Horizontal Protection Level,HPL）和垂直保护级别（Vertical Protection Level,VPL）进行计算。

对应每个子估计的HPLi由两部分组成：1）子估计Xi与主估计X0差值的门限,即由误警率Pfa计算得到的检测门限Ti（i=1,2,…,n）；2）子估计本身的水平位置误差门限ai（i=1,2,…,n）, 即

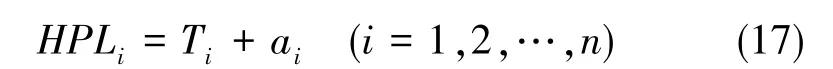
对应子估计的误差协方差阵的定义和计算公式如下

给定漏检率Pmd,则水平位置误差门限ai（i=1,2,…,n）的计算公式如下

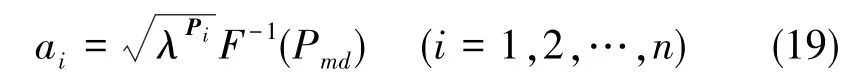
式（19）中,λPi为对应Pi水平位置方向上的最大特征值, 可由Pi（1,1）、Pi（1,2）、Pi（2,2）计算得到。

综上所述,多解分离法的水平保护级别计算方法为

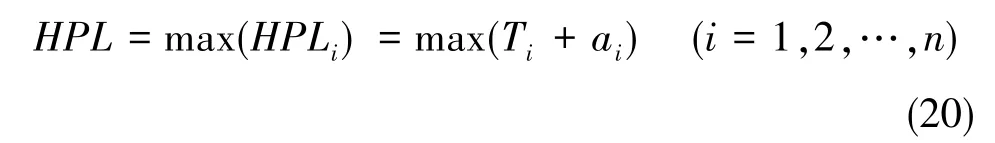
同理,多解分离法的垂直保护级别计算方法为

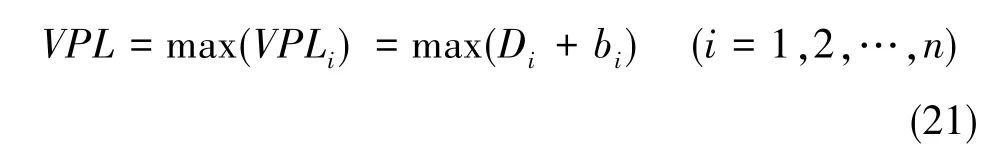
式（21）中,

3 仿真结果与分析

为了验证本文提出的完好性监测算法的有效性,建立了一套数字仿真平台,包括飞行轨迹模拟器、卫星星座模拟器、大气数据模拟器、卫星接收机模拟器等,分别采用本文的设计算法及传统RAIM算法进行仿真实验,对比两者完好性监测性能。如图2所示,载体飞行航迹为动态航迹,包括加速爬升、巡航飞行、机动转弯等动作,仿真时间为3600s。卫星星座由24颗卫星构成,设定可见星仰角为7.5°,观测频率为1Hz,伪距观测噪声的标准差为33.3m,气压高度表测量误差的标准差为50m。

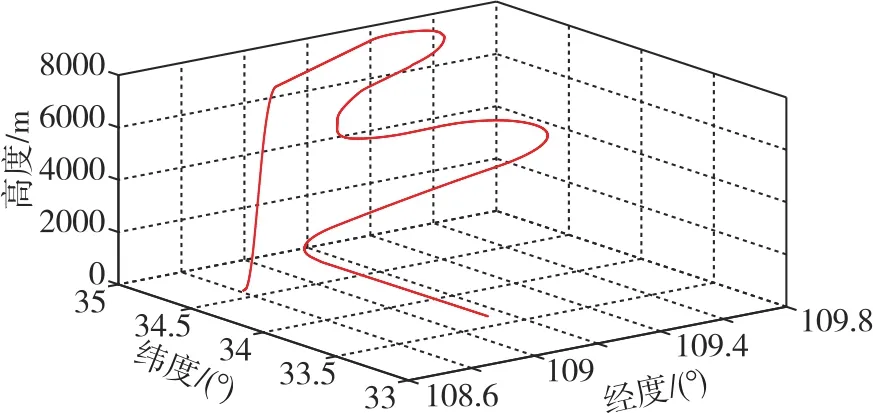
图2 载体飞行航迹仿真示意图Fig.2 Simulation diagram of the flight path

载体在飞行过程中的可见星数和卫星编号如图3所示。

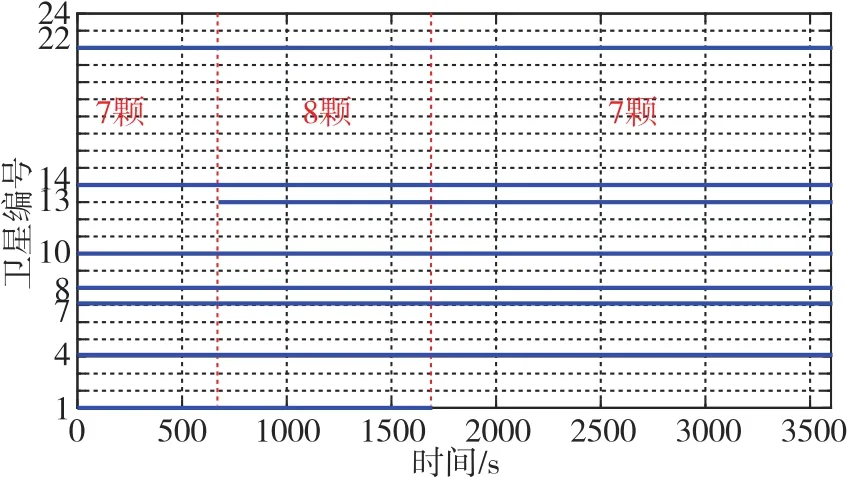
图3 飞行过程中可见星选取情况Fig.3 Selection of visible satellites during the flight

根据民航运行相关规范［16］,设定卫星故障检测的误警率为1×10-5,漏检率为1×10-3,可得到两种方法在飞行过程中的保护级别值,如图4、图5所示。

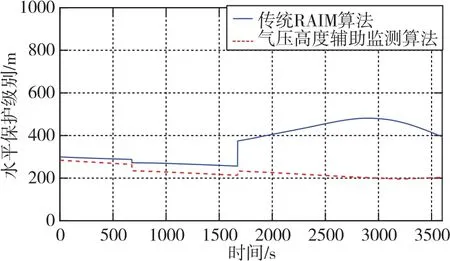
图4 两种算法的水平保护级别对比Fig.4 Comparison of HPL between the two algorithms

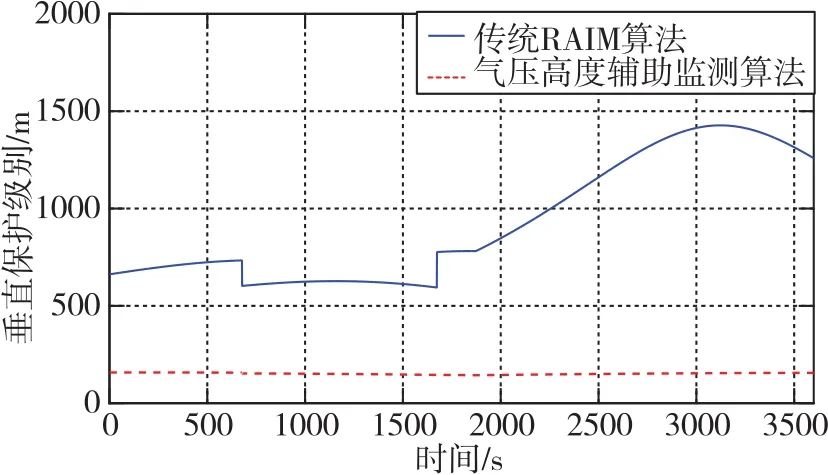
图5 两种算法的垂直保护级别对比Fig.5 Comparison of VPL between the two algorithms

由图4、图5可知,载体在飞行过程中,当可见卫星数发生变化时,计算得到的保护门限值会发生跳变,即可见卫星数会影响算法的可用性。同时,可以看出本文所提出算法的保护级别值均优于传统RAIM算法,尤其是在垂直方向上的性能有了显著提升,从而有效保证了完好性监测算法的可用性。

同时,为了测试对比算法的故障诊断能力,在航迹运行至2000s～3000s阶段,在假设仅有5颗可见卫星（4号、8号、10号、13号、14号）的情况下,在10号卫星伪距中注入1000m的故障偏差。此时,传统RAIM算法只能实现卫星故障的检测而无法进行准确识别。下面给出两种算法下卫星导航系统自身解算位置的误差对比曲线,如图6、图7所示。

两组误差对比曲线的统计结果如表1所示。

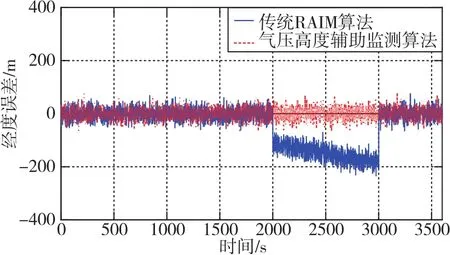
图6 两种算法的经度误差对比曲线Fig.6 Comparison curves of longitude error between the two algorithms

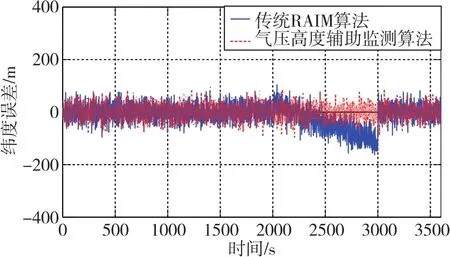
图7 两种算法的纬度误差对比曲线Fig.7 Comparison curves of latitude error between the two algorithms

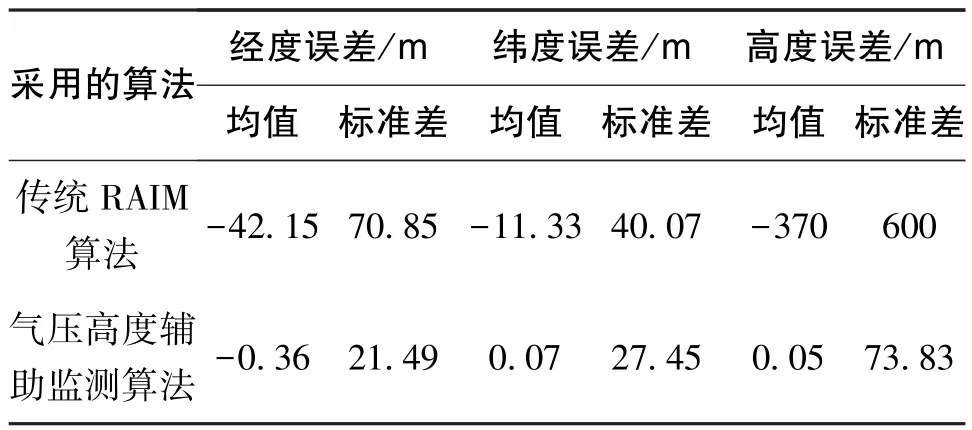
表1 两种算法的位置误差统计结果Table 1 Statistical results of position errors between the two algorithms

在卫星发生故障时,此时的可见星数为5颗。根据RAIM算法原理,传统RAIM算法只能实现故障检测,但无法完成故障的准确识别和隔离,从而导致误差曲线发生跳变,影响卫星导航系统的定位精度。仿真结果表明,本文提出的算法经度误差标准差减少到了21.49m,纬度误差标准差减少到了27.45m,高度误差标准差减少到了73.83m,分别为传统 RAIM算法的 30.3%、68.5%、0.12%。这是由于新算法引入了外部高度信息作为辅助,在卫星数为5颗的情况下仍然可用,并联合实现故障监测,能及时准确地检测和定位出故障卫星并隔离,从而有效保障了卫星导航系统的精度和可靠性。

4 结论

针对卫星导航系统RAIM算法在可用性上的不足,本文提出了一种气压高度表辅助的机载自主完好性监测算法,该算法有效合理利用了气压高度表提供的冗余高度信息,结合卫星导航系统的自身观测量,建立了联合系统的观测模型,推导了基于多解分离的完好性监测算法,实现了故障卫星的诊断及保护级别的计算,并进行了仿真验证。仿真结果表明,本文提出的算法经度误差标准差减少到了21.49m,纬度误差标准差减少到了27.45m,高度误差标准差减少到了73.83m。相比于传统的接收机自主完好性监测算法,该算法在可见星为5颗时仍能识别故障卫星,具有更好的可用性和故障检测能力,能有效提高卫星导航系统的完好性监测性能。