基于视觉导航仓储AGV的模糊PID控制

周阔海,黄 民,高 宏,郎需强

(北京信息科技大学 机电工程学院，北京 100192)

0 引言

自动导引运输车(automatic guided vehicle，AGV)在柔性制造业、物流业以及自动化仓储中具有广泛的应用前景，它提高了工厂内货物搬运的作业效率，降低了人工成本，减少了企业内部由于物流环节冗余和辛苦的重复动作所造成的不必要的物力和人力的浪费。

在智能车辆的自主导航中，在地面上张贴标识线由二维视觉传感器进行图像识别的导航方法，由于其引导路径的设置和变更相对容易、技术成本低，并且与其他视觉导航方法如三维视觉识别相比，具有图像处理速度快、控制实时性较好等特点，已成为AGV导航的一个主要发展方向。在控制领域，传统PID控制方法具有结构简单且使用方便等特点。但在实际应用中，AGV运动控制中应用传统PID会出现漂移、震荡等响应速度慢、位置不准确和鲁棒性差等缺点，不利于效率的提高。而模糊控制适用于非线性、参数变化大、强耦合，难以获得精确数学模型的控制系统。将模糊控制和PID控制结合起来，使得控制变量能够实时整定，可以较好解决以上问题。

本文设计并制作了仓储搬运货物AGV，采用了二维视觉传感器识别地面标识线自主导航的方式，使用4个对称正交分布式全向轮作为行走机构，并在此基础上应用模糊PID控制方法优化AGV的行走稳定性，提高AGV工作效率。

1 仓储AGV控制系统

1.1 AGV底盘运动学模型

本文设计的仓储搬运货物AGV底盘为正交分布的双排全向轮，每一个全向轮分别由一个伺服电机驱动，电机型号为JM-CP6248，输出扭矩为0.52 N·m，额定转速为5600 r/min，电机驱动型号为Copley AE2，此驱动器能控制两路输出，故AGV底盘使用了两个驱动器。

建立AGV运动模型之前，作如下假设：假设AGV底盘是刚体，不考虑形变；假设全向轮做纯滚动；假设地面是光滑平坦表面。

如图1所示，定义AGV的4个全向轮分别为W1、W2、W3、W4，以AGV底盘质心为原点建立坐标系xP0y。设定AGV运动坐标系，以AGV中心点为原点，对称轴为x轴，各轮的轴心在坐标系xP0y的位置向量长度为L1、L2、L3、L4，取逆时针方向为正方向。

图2是单个全向轮的运动分析，各轮的运动方向向量为Di；各轮与Li垂直方向的向量为Ti；设Di与x轴的夹角为αi，Ti与x轴的夹角为γi。AGV的速度是4个全向轮速度的合成，4个直流无刷伺服电机各驱动一个全向轮，要求AGV平稳准确地运动就需要合理地分配4个全向轮的转速，建立各轮速度和AGV整体速度之间的运动学模型是仿真研究的基础。

以轮1为例，AGV整体速度为V，在绝对坐标系VxOVy中，全向轮的速度可分解为可控的切向速度Vq和不可控的法向速度Vf,其中Vx与Vy垂直，Vq与Vf垂直，则有

V=Vx+Vy=Vq+Vf

(1)

Vqi=Vx·cosαi+Vy·sinαi=

(2)

Vq=R(θ)·Vqi=

(3)

其中R(θ)为旋转矩阵：

(4)

全向轮切线方向不垂直于底盘形心与轮子的连线，有

Vq=VθLicos(γi-αi)

(5)

式中Vθ为AGV整体运动的角速度，联立式(3)～(5)有

(6)

式中v1、v2、v3、v4为全向轮线速度。

(7)

式中：ω为AGV整体运动的角速度；ωi为单个全向轮的角速度。

当把位置指令和速度指令发送到控制器，控制器会依照式(7)计算出每个轮子相应的速度并下达指令，保证AGV能够以要求的速度到达指定的位置。

1.2 AGV控制过程

如图3所示，AGV视觉导航采用微软LifeCam Studio摄像头，摄像头捕捉地面粘贴的红色标识线，捕捉到的画面通过膨胀和腐蚀视觉方法分割出图像中的红色区域。用OpenCV中求最小外接矩形的命令，得出图像中红色标识线的方向，即斜率k，同时，生成红色标识线纵向的中心线。根据直线方程y=kx+b，求出中心线与水平轴的交点坐标(x,y),其中x是偏移量。

由参数k和b计算出AGV的偏移角度eθ和偏航距离ep，规定红色标识中心线位于y轴右侧为正，左侧为负，则：

(8)

eθ=arctank

(9)

仓储AGV闭环控制系统框图如图4所示。系统由5部分构成，包括控制器、驱动器、伺服电机、视觉传感器和机械传动部分。其中伺服电机上的编码器可以实时反馈AGV位置信息，视觉传感器反馈AGV的偏转角度eθ和偏移距离ep信息，负反馈和输入参数经过控制器进行计算，把运算完成后分解的速度通过驱动器传输给4个独立伺服电机，4个伺服电机通过减速器带动4个全向轮，最终完成把货物运输到指定区域的目的。编码器负责反馈运动距离d。

然而，有些调研，根本不利于工作。据中央电视台《焦点访谈》报道，在江西某市辖区，2017年7月的22个工作日中，先后有12名市厅级干部到区里调研。几点几分到哪里，参观什么、听谁介绍、停留多长时间，几点几分离开，前往下一个地方，都有完备“脚本”。而有些地方更是像打造旅游路线一样打造“经典调研线路”，无论什么调研主题，领导干部们走的都是同一条线，访的是同一批对象，听的是同一套说辞。

AGV实物如图5所示，上部分为辊子平台，AGV通过平台上左侧的光电传感器检测是否有货物放置，当检测到有货物放到辊子平台上时，AGV会自动把货物运送到卸货站点，并通过辊子滚动进行卸货动作。卸货站点的高度与AGV一致。

2 模糊PID控制器

2.1 PID控制原理

PID控制是根据系统的误差，利用比例(P)、积分(I)、微分(D)计算出控制量对原有系统进行调节，其数学表达式为

(10)

其中比例部分为

KP·e(t)

(11)

比例环节阶段，输出值在目标值与实际值产生偏差的瞬间向着误差减少的方向变化。

积分部分的数学表达式为

(12)

微分部分的数学表达式为

(13)

PID中的微分环节实际上就是在偏差变化的瞬间，根据偏差的变化趋势预先给出适当的纠正。偏差变化得越快，微分控制器的输出越大，输出值在偏差值变大之前修正。这对系统克服振荡、减小超调量，以及系统稳定起到了较为积极作用，系统纠偏的跟踪速度得到提升。但是微分对于输入信号的噪声比较敏感，噪声比较大的系统一般不适用微分，或者在信号输入之前进行滤波。

2.2 模糊PID控制器原理

模糊PID控制器的基本结构如图6所示。

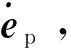
为了进一步提高系统的响应和执行速度，采用改进的模糊控制器[10]。控制器原先采用位置式PID，控制的是KP、KI、KD这3个参数，而现在改为控制其增量，即ΔKP、ΔKI、ΔKD，3个增量的变化小，计算量少[10]。参数模糊PID控制器表达式为

KP(n)=KP(n-1)+ΔKP

(14)

KI(n)=KI(n-1)+ΔKI

(15)

KD(n)=KD(n-1)+ΔKD

(16)

2.3 模糊PID控制器的设计

2.3.1 模糊语言变量的确定

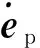
2.3.2 隶属度函数的确定

输入隶属度函数以及输出隶属度函数选择三角函数，如图7所示。

2.3.3 模糊控制规则

根据文献[11]归纳出的控制过程中自整定原则，并依据大量的实验经验，得出输出变量的模糊控制规则如表1所示。

表1 ΔKP、ΔKI、ΔKD模糊控制规则

2.3.4 去模糊化

依据表1，根据模糊控制规则完成输出变量的动态调整，得出模糊化的输出参数后采用重心法实现去模糊化，再根据式(14)～(16)即可得到在模糊控制后的PID值。

3 仿真实验

3.1 Matlab建模

在Matlab/Simulink中搭建模糊控制器，如图8所示。其中Fuzzy Logic Controller子模块根据表1进行封装，PID子模块为增量式PID仿真模型。采用Ziegler-Nichols以及试凑法确定参数，输入为阶跃信号，幅值设定为1，仿真时间长度为15 s，系统采样时间为0.01 s，前置增益为0.2，设定初始PID值KP=0.5，KI=0.01，KD=0.001。

3.2 结果分析

本文中的AGV采用了BECKHOFF控制器，开发软件是控制器自带软件TwinCAT3。使用TwinCAT3中的Matlab/Simulink编程模块接口对AGV运动控制器进行模糊PID控制算法的添加，进行真实场景下的实验。通过TwinCAT3软件中ScopView功能采集AGV速度及实时位置偏差，并进行分析。

使用TwinCAT3中的函数块FB_BasicPID进行传统PID控制，得到误差曲线，如图9～10所示。

图9为小车最大速度在0.55 m/s时采集到的数据，可以看出AGV运动过程中位置偏差最大达到8.5 mm，平均误差为4.5 mm。图10为AGV速度为1.1 m/s时所采集到的数据，其误差最大达到5 mm，平均误差为3 mm。对比发现，当速度提高一倍之后，AGV的实时位置偏差增大了35%。这是因为在AGV运动过程中，底盘有相对于标识线的偏移误差变量。该变量是由AGV移动过程中全向轮的不连续性和打滑现象以及地面环境因素所造成的，并且随着速度的增大而增大，故使用传统PID控制很难满足实用性要求。

应用模糊PID进行控制时的误差曲线如图11～12所示。

从图中可知，应用模糊控制之后，AGV设定移动距离与实时移动距离在AGV最大速度分别为0.55 m/s和1.1 m/s时所采集到的位置偏差是比较稳定的。经过多次实验之后得出的数据显示，最大值均小于5 mm。

再进行AGV的运货效率测试，测试环境中，每个货堆尺寸为1×1.2 m，相邻两个货堆间隔10 cm，在应用传统PID算法的情况下，AGV运输货物的效率平均为每小时拣货350件左右，而运用模糊PID控制方法后平均运送效率能达到每小时370件左右，运货效率提高了5%。

4 结束语

本文针对由全向轮驱动的AGV在运动过程中出现的打滑、偏移等问题，将传统PID控制方法和模糊控制方法相结合，采用模糊PID控制方法来提高AGV运动过程的稳定性。在图像传感器反馈偏航距离并同时由编码器反馈运动距离的情况下，对比实验结果表明，AGV运动过程中应用模糊PID控制方法较传统PID控制方法，其运动精度和稳定性有所提高。

由于本文在模糊PID控制方法中的输入参数只考虑了AGV在运动过程中的偏航距离误差和误差变化率，并没有考虑AGV偏转角度的误差，这两种误差合成后经由模糊PID控制方法输出的AGV速度变化还需进一步论证；模糊PID控制方法中输入输出参数的隶属函数和模糊规则，仅依靠部分实验数据和主观人为因素进行确定，如果能够结合神经网络进行自主学习确定隶属函数和模糊规则，是否能够进一步提高AGV运送效率，还需要进行试验讨论。