老年人“踝关节策略”静态与动态平衡能力的相关分析

游永豪，邵梦霓，胡燕杰，张 阳，王广磊，朱靖靖

人体平衡能力主要受视觉、前庭觉、本体感觉影响，衰老会使人的视觉、前庭觉、本体感觉出现一定程度的退行性变化，从而降低平衡功能。平衡功能减弱，是引发老年人发生跌倒的主要原因，平衡能力是预测老年人跌倒风险的重要指标[1]。2011年9 月，卫生部颁布的《老年人跌倒干预技术指南》指出：“跌倒是我国伤害死亡的第4位原因，而在65岁以上的老年人中则为首位。老年人跌倒死亡率随年龄的增加急剧上升”。

人体平衡可分为静态平衡和动态平衡。目前，通常采用平衡能力测试仪测试人体站立状态下的静态和动态平衡控制能力。人体站立状态下的平衡控制方式有踝关节策略、髋关节策略和迈步策略3 种[2]：踝关节策略，是指干扰力较小且支撑面较硬时，人体主要通过踝关节的角度和力量控制平衡；髋关节策略，是指干扰力较大且快时主要通过髋关节控制平衡；迈步策略，是指干扰力很大使人体重心移动到支撑面以外时通过迈步方式控制平衡[3-4]。静态平衡能力测试仪通常要求受试者站立在很小、坚硬、平整且稳定的平衡踏板上，尽力维持身体姿势的稳定；动态平衡能力测试仪要求受试者站立在很小、坚硬、平整但是很不稳定的平衡踏板上，尽力维持平衡踏板的水平稳定，或按照预定方式旋转平衡踏板。以上平衡测试方法均不需要通过迈步策略维持平衡，而是主要通过踝关节策略和髋关节策略的双重作用维持平衡，这就无法区分踝关节策略和髋关节策略对老年人平衡能力的贡献度，也无法判断两者的代偿作用。因此，有必要在排除髋关节策略的情况下，开展对老年人踝关节策略静态、动态平衡能力方面的研究。

目前，国内外对老年人平衡能力的研究大多集中在运动干预[5-7]、测评方法[8-9]和疾病影响[10-12]等方面，几乎未曾对静态与动态平衡能力的相关性进行探索。事实上，弄清老年人静态与动态平衡能力的关系，对指导老年人锻炼平衡能力具有重要的实践意义，对相关研究也能提供理论参考。若两者存在正相关关系，那么老年人锻炼静态平衡能力的同时也在一定程度上提升了动态平衡能力；若两者存在负相关关系，那么老年人锻炼静态平衡能力的同时会损失一部分动态平衡能力；若两者不存在相关关系，那么老年人需要同时锻炼静态与动态平衡能力。本研究通过对28 名社区老年人“踝关节策略”静态平衡和动态平衡能力的实验测试，采用简单相关和典型相关等方法，旨在探索老年人“踝关节策略”静态与动态平衡能力的相关性。

1 研究对象与方法

1.1 实验对象

实验对象为28 名社区女性老年人。为尽量控制年龄、身高、体重、运动习惯对结果的影响，选取的老年人在以上指标的个体差异都不大，变异系数均小于0.15。年龄变异系数0.10[（66.4±6.4）岁]，身高变异系数0.03[（157.1±4.8）cm]、体重变异系数0.13[（63.0±8.5）kg]。纳入标准：四肢健全，有独立生活能力，在无辅助器械的情况下能独立行走100 m以上。排除标准：有锻炼习惯，存在平衡功能障碍，近1 年内下肢做过外科手术。本研究得到伦理委员会同意，实验前受试者签署了书面知情同意书。

1.2 静态平衡能力测试

1.2.1 测试仪器 静态平衡能力测试使用中国科学院研制的IIM-BAL-100静态平衡能力测试仪。该设备采用高精度三维测力传感器获取人体不同站立状态下的压力中心信息，并绘制静态姿势图，评估人体静态平衡能力。

1.2.2 测试指标 站立状态包括双足站立睁眼测试（Double foot with eyes open，DO）、双足站立闭眼测试（Double foot with eyes closed，DC）、线性步站立睁眼测试（Linear step with eyes open，LO）和单足站立睁眼测试（Single foot with eyes open，SO）。

测试完成后，静态平衡能力测试仪自动给出双睁得分、双闭得分、线睁得分、左睁得分和右睁得分，以及各站立状态的包络面积（Area）、轨迹长（Lng）和单位面积轨迹长（Lng/A）。

双睁得分、双闭得分和线睁得分，分别为双足睁眼、双足闭眼、线性步睁眼站立时的静态平衡能力得分；单睁得分为左足和右足睁眼站立时静态平衡能力得分（左睁得分与右睁得分的均值）；包络面积（Area）为压力中心轨迹所覆盖的最大闭合面积；轨迹长（Lng）为压力中心轨迹的长度；单位面积轨迹长（Lng/A）为轨迹长与包络面积的比值。静态综合得分为双睁得分、双闭得分、线睁得分和单睁得分的均值。

1.2.3 测试方案 测试步骤：（1）自然条件（可以采用髋关节调节身体平衡）下测试1 次“自然状态”静态平衡能力；（2）佩戴条状夹板适应性测试1次“踝关节策略”静态平衡能力；（3）拆除夹板测试1次“踝关节策略”静态平衡能力。

“自然状态”静态平衡能力测试：受试者脱鞋，两眼平视前方，双臂自然下垂于身体两侧，不得摆动；躯干挺直，双足站立时足跟点间距为10 cm；单足站立睁眼测试包括左足站立和右足站立2种情况，腾空腿抬至脚底与支撑腿内踝平齐；线性步睁眼测试时使受试者非优势足在前、优势足在后，优势足尖抵非优势足跟，两足站成一条直线；每种站立状态的测试均有3～6 s的准备时间，测试时长均为10 s。

佩戴夹板情况下“踝关节策略”静态平衡能力测试：在“自然状态”基础上，给受试者佩戴条状夹板固定其髋关节角度，让受试者掌握仅通过踝关节控制静态平衡的方法。条状夹板（竹板加工）为自制辅助测试器材，共10个，每个长40 cm，宽4～5 cm。测试时，垂直方向置于髋关节四围，髋关节前后各4个，左右各1个，用弹性绷带环状固定。

拆除夹板情况下“踝关节策略”静态平衡能力测试：在“自然状态”的基础上，让受试者根据所掌握的佩戴夹板时控制静态平衡的方法，仅通过踝关节控制身体平衡。拆除夹板进行测试的原因：排除夹板本身对静态平衡能力的影响。

优势足的判定方法：实验前在受试者前方3 m 处放1 个软排球，请受试者向前行走踢球，踢球足可判定为优势足。连续测3次，3次结果一致时判定结束；3次结果不一致时，重复以上测试。

1.3 动态平衡能力测试

1.3.1 测试仪器 动态平衡能力测试使用德国Dr-Wolff 公司生产的Balance-check 动态平衡能力测试仪。该设备根据人体在不稳定平衡板上站立时平衡板的倾斜情况绘制动态平衡姿势图，评估人体动态平衡能力。测试难度为中等，控制设备选择sensor+高敏传感器。目标球会随平衡板的倾斜向低处滑动，平衡板倾斜角度越大，目标球滑动速度越快（见图1）。

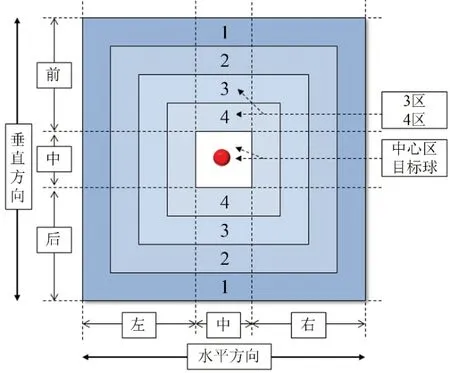
图1 动态平衡测试指标示意图Figure1 Schematic Diagram of the Dynamic Balance Test Indicators

1.3.2 测试指标 实验完成后，仪器直接生成测试指标，主要指标包括动态得分（Dynamic score）：目标球在各区域停留时间换算分数；旋转速度（Rot.speed）：平衡板在单位时间内倾斜的角度；最大旋转速度（Rot.speed Max）：测试过程中平衡板在单位时间内倾斜的最大角度；目标球在各区域的停留时间百分比：目标球在某区域停留时间与测试总时间的比值（见图1）。

1.3.3 测试方案 采用与静态平衡能力测试类似的方法，具体是：（1）“自然状态”动态平衡能力测试：受试者脱鞋，两眼平视前方，双臂自然下垂与身体两侧，不得摆动，躯干挺直，可同时采用髋、踝两关节控制身体平衡；（2）佩戴夹板情况下“踝关节策略”动态平衡能力测试：在“自然状态”的基础上，给受试者佩戴条状夹板固定其髋关节角度，让受试者掌握仅通过踝关节控制动态平衡的方法；（3）拆除夹板情况下“踝关节策略”动态平衡能力测试：在“自然状态”的基础上，让受试者根据所掌握的佩戴夹板时控制动态平衡的方法，仅通过踝关节控制身体平衡。

1.4 信效度检验

1.4.1 信度检验 为检验实验测试的内部一致性信度，对其中10名老年人拆除夹板后多测2次静态平衡能力，Cronbach'sα信度系数为0.91；对所有老年人拆除夹板后多测2 次动态平衡能力，Cronbach'sα信度系数为0.96。可见，本研究设计的静态、动态平衡能力测试结果信度非常高。

1.4.2 效度检验 为检验“踝关节策略”静态、动态平衡能力测试方法的有效性，本研究通过比较“自然条件”、佩戴夹板、拆除夹板3种情况下的平衡能力，检验实验测试的区分效度，验证测试方法的有效性。

数据显示，静态综合得分与动态得分的对比结果具有较高的一致性。分别用a、b、c代表“自然条件”、佩戴夹板、拆除夹板3种情况下的平衡能力。a明显大于b（P＜0.05），说明佩戴条状夹板，限制了髋关节对平衡的调控作用，此时受试者仅通过踝关节控制平衡，平衡能力明显降低；b 与c 基本一致（P＞0.05），说明拆除夹板后，受试者掌握了只使用踝关节控制平衡的方法（见图2）。以上证明本研究设计的“踝关节策略”平衡能力测试方法有效。

图2 3次测试的静态综合得分、动态得分对比结果Figure2 Comparison of Static Comprehensive Scores and Dynamic Scores of Three Tests

1.5 数据处理与分析

本研究结果中所使用的为拆除夹板后测试的数据。老年人静态综合得分以及不同站立状态下的静态得分与动态得分的相关性采用Pearson积差相关系数，静态平衡与动态平衡“指标集”的选取方法采用因子分析法，“指标集”间的相关分析采用典型相关分析法。相关系数检验的显著性水平取0.05，非常显著性水平取0.01。

2 结 果

2.1 静态平衡与动态平衡的Pearson积差相关分析

静态综合得分是对老年人静态平衡能力的总体评价，是不同站立状态下静态平衡能力得分的均值；动态得分是对老年人动态平衡得分的总体评价。老年人静态综合得分以及不同站立状态时的静态得分与动态得分的相关系数均不具有统计学意义（P＞0.05），说明老年人静态平衡能力与动态平衡能力不存在相关性（见表1）。

表1 老年人静态平衡与动态平衡的相关系数一览表Table1 List of Correlation Coefficients Between Static Balance and Dynamic Balance of the Eelderly

但是，静态平衡和动态平衡都分别包括多个具体的评价指标，这些指标之间可能会存在一定的相关性，这些相关性预示着静态平衡与动态平衡可能会存在一定的内部联系。由于指标过多，构建简单的相关矩阵难以发现指标之间的内部联系，因此本研究采用因子分析法对静动态平衡能力指标进行筛选、提取公因子，把公因子载荷较大的指标组成“指标集”，通过“指标集”间的典型相关分析，探索静态与动态平衡的相关性。

2.2 静动态平衡能力的因子分析

纳入的静态平衡能力指标是双足睁眼、双足闭眼、线性步睁眼、单足睁眼4种站立状态下的轨迹长、包络面积和单位面积轨迹长。纳入的动态平衡能力指标是旋转速度，最大旋转速度，目标球在水平方向左、中、右区域时间百分比，目标球在垂直方向前、中、后区域时间百分比，目标球在3、4、中心区停留时间百分比等。

满足下列条件之一者剔除有关变量：提取的公因子方差小于0.6；在2 个以上公因子上的因子载荷近似相同。采用KMO 和Bartlett 球形检验进行因子分析的条件检验，特征值大于1 的条件下采用主成分法提取公因子，最大方差法进行因子旋转。

筛选变量过程中，静态平衡能力指标中双足闭眼和单足睁眼状态下的单位面积轨迹长公因子方差均小于0.6（分别为0.585和0.570），但是提取的静态平衡公因子均是按照站立状态聚类（每种站立状态下的指标明显归为一类），而且因子载荷都较高，为了使静态平衡能力各公因子指标对称且方便解释，保留了这2个指标。筛选变量后，静态平衡能力指标全部保留，动态平衡能力指标保留了旋转速度、中心区时间、水平方向和垂直方向的中间区域时间百分比。KMO 为0.783，Bartlett 球形检验P＜0.01，说明适合因子分析，提取的公因子方差见表2。除双足闭眼和单足睁眼状态下的单位面积轨迹长公因子方差较小外（前面已经解释保留的原因），其余指标的公因子方差均在0.75以上，说明指标信息大部分被提取（见表2）。

特征值大于1 的条件下，采用主成分法共提取了5 个公因子，累积方差贡献率84.5%。说明所提取的公因子包含足够的信息量，因子分析效果较好（见表3）。共提取1个动态平衡能力公因子，包括Center、VM、HM和Rot.speed 4个指标，命名为“动态平衡能力”（简称动态），4 个指标因子载荷的绝对值都大于0.8（见表4）。

表2 提取公因子方差一览表Table2 List of Extracting the Common Factor Variance

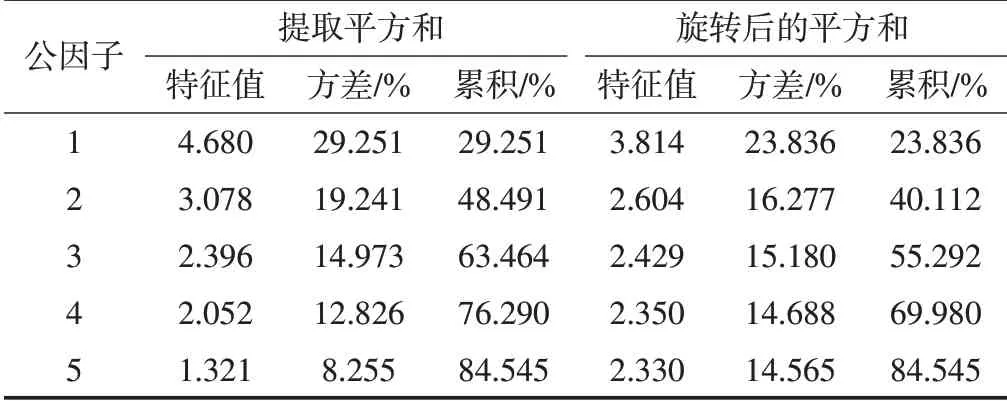
表3 提取公因子的特征值、方差贡献率一览表Table3 List of Eigenvalues and Variance Contribution Rates for Extracting Common Factors

表4 公因子载荷表Table4 list of Common Factor Load

共提取4 个静态平衡能力公因子，分别代表4 种站立状态时的静态平衡能力，按特征值由大到小可分别命名为“线性步睁眼静态平衡能力”（简称线睁静态）、“单足睁眼静态平衡能力”（简称单睁静态）、“双足闭眼静态平衡能力”（简称双闭静态）、“双足睁眼静态平衡能力”（简称双睁静态）。4 个公因子都包括轨迹长、包络面积和单位面积轨迹长3 个指标。

2.3 静态平衡与动态平衡能力的典型相关分析

根据因子分析中静态平衡和动态平衡所提取的公因子，以及公因子所包含的指标集，采用典型相关法进一步探索静态平衡与动态平衡的相关性。结果显示，老年人踝关节策略动态平衡能力与双足睁眼、单足睁眼状态的静态平衡能力相关系数均不具有统计学意义（P＞0.05），与双足闭眼、线性步睁眼静态平衡能力的典型相关系数均具有统计学意义（P＜0.05），且相关性较高（见表5）。

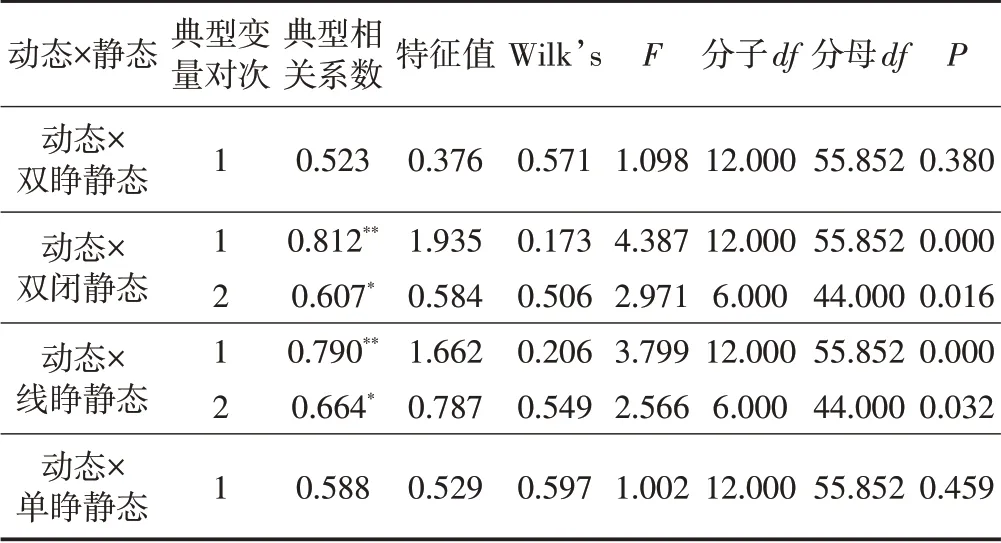
表5 典型相关系数结果表Table5 Table of Typical Correlation Coefficient Results

指标的标准化换算系数的绝对值越大，说明指标对典型变量的贡献越大（见表6）。为确切了解各指标对典型变量的贡献顺序，对有显著性的典型相关分析中，各站立状态的标准化换算系数取绝对值，并从小到大排序（见表7）。

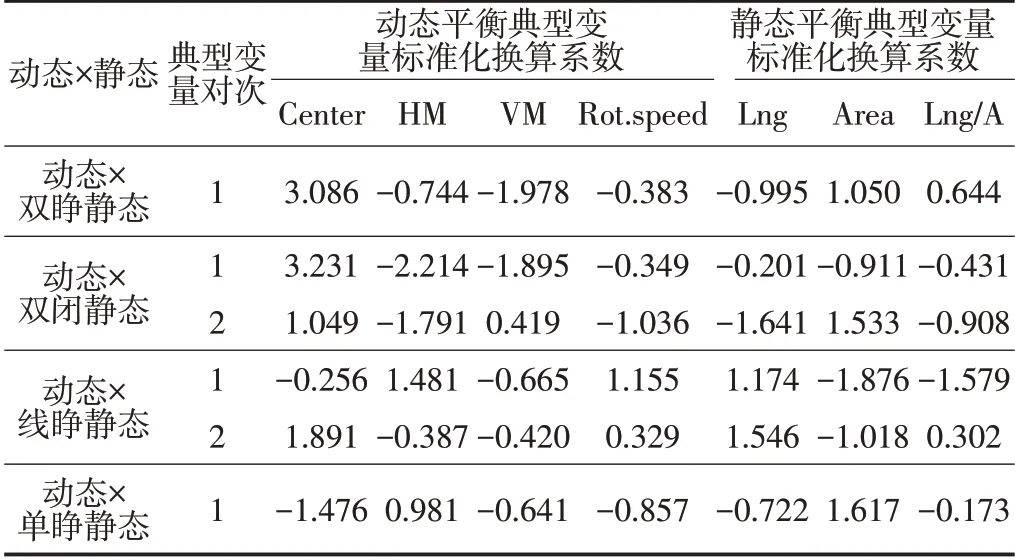
表6 典型变量标准化换算系数结果表Table6 Table of Typical Variables Conversion Factor Results

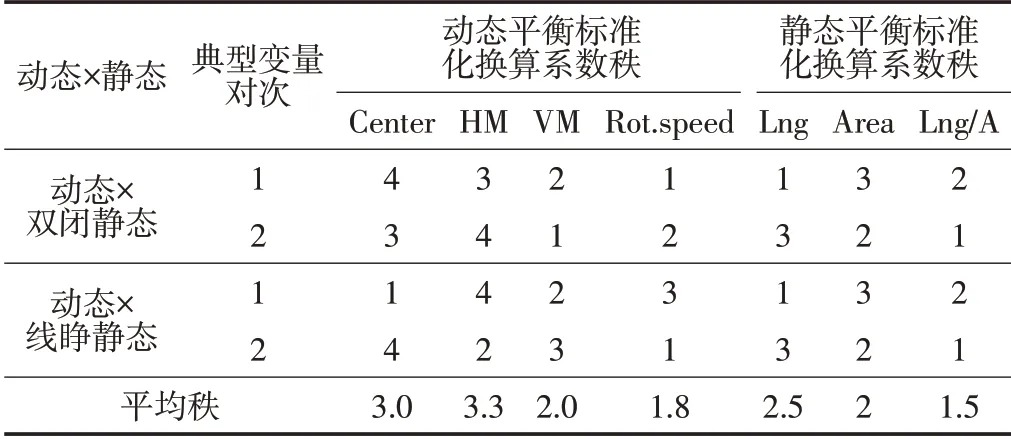
表7 典型变量标准化换算系数排秩结果表Table7 Table of Typical Variables Normalized Conversion Coefficient Rank Results

动态与双闭静态典型相关分析的第1 对典型变量中，对代表动态平衡的典型变量U1贡献较高的指标为Center和HM，对代表静态平衡典型变量V1贡献较高的指标为Area和Lne/A；第2对典型变量中，对代表动态平衡的典型变量U2贡献较高的指标为HM和Center，对代表静态平衡典型变量V2贡献较高的指标为Lng和Area（见表7）。

动态与线睁静态典型相关分析的第1 对典型变量中，对代表动态平衡的典型变量U1贡献较高的指标为HM和Rot.speed，对代表静态平衡典型变量V1贡献较高的指标为Area和Lne/A；第2对典型变量中，对代表动态平衡的典型变量U2贡献较高的指标为Center和VM，对代表静态平衡典型变量V2贡献较高的指标为Lng和Area（见表7）。

总体而言，在动态平衡与双足闭眼和线性步睁眼静态平衡的典型相关中，对动态平衡贡献较大的指标是Center 和HM，对双足闭眼和线性步睁眼静态平衡贡献较大的指标是Lng和Area。

典型载荷是原始变量与其典型变量之间的相关系数。2次提取典型变量时，相关系数的差异性在一定程度上也能体现所提取信息的差异性。一般而言，差异性越大，典型变量对样本信息的概括性越好。

动态与双闭静态的典型相关分析中，第1对典型变量和第2对典型变量对应的相关系数方向相反，说明2 次提取的动态或静态成分差异较大（见表8）。

动态与线睁静态的典型相关分析中，动态平衡各指标与2次提取的典型变量（U1和U2）的相关系数方向相反，说明2次提取的动态成分明显不同。静态平衡各指标与2次提取的典型变量（V1 和V2）的相关系数大小差异较大，其中Lng/A 的符号相反，说明2次提取的静态成分也明显不同（见表8）。

表8 典型载荷结果表Table8 Table of Typical Load Results

交叉载荷体现了原始变量与其对立的典型变量之间的相关系数，表示原始变量被其对立典型变量预测的可能性。以相关系数的绝对值大于0.5 为标准，动态与双闭静态典型相关分析中，与V1具有一定相关性的为HM，与U1具有较高相关性的为Lng 和Area，与U2 具有一定相关性的为Lng/A；动态与线睁静态典型相关分析中，与V1具有一定相关性的为Rot.speed，与U1 具有较高相关性的为Lng/A，与V2 具有一定相关性的为Center（见表9）。

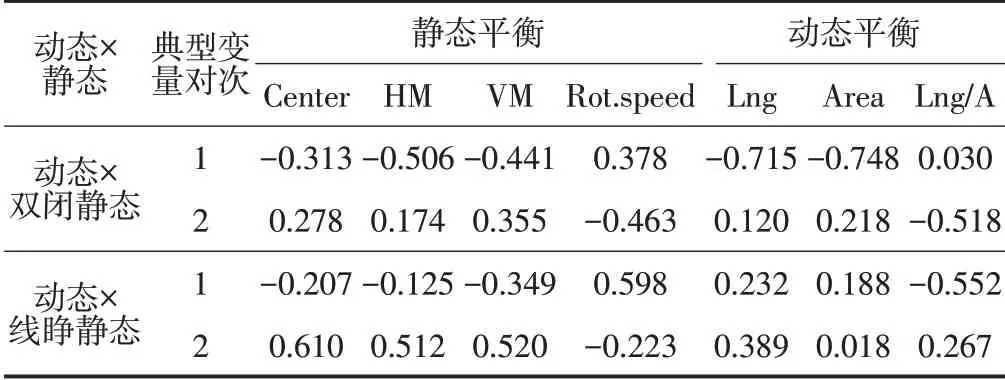
表9 交叉载荷结果表Table9 Table of Cross Load Results

3 讨 论

由于平衡能力测试本身也是一种平衡能力训练，很可能会产生“练习效应”（前面的练习影响后面的测试结果，造成连续多次平衡能力测试的结果不同），从而对测试的信度产生影响。信度是反映测试数据可靠性的重要指标，因此有必要检验实验测试的信度。卫生部2011年发布的《老年人跌倒干预技术指南》指出，步态的稳定性下降和平衡功能受损是引发老年人跌倒的主要原因[13]。袁空军等[14]指出，动态平衡能力在评估跌倒风险时更有效。因此，课题组在前期已经对老年人“踝关节策略”动态平衡能力测试的信度进行了重点研究，动态得分的Cronbach'sα信度系数为0.96[15]，为本研究提供了重要的理论基础。本研究采用同样的方法，又检验了老年人“踝关节策略”静态平衡能力测试的信度，静态综合得分的Cronbach'sα信度系数为0.91。可见，本研究中的静态、动态平衡能力测试数据非常可靠。但是我们还发现，老年人的静态与动态平衡能力可能存在相关关系，这对老年人平衡能力的锻炼具有重要的指导意义。具体是两者间存在正相关关系时，静态和动态平衡能力会相互促进，老年人可以选择相对较弱的一种平衡能力进行锻炼；存在负相关关系时，静态和动态平衡能力会相互制约，老年人锻炼任意一种平衡能力时，需要同时预防另一种平衡能力的降低；不存在相关关系时，老年人需要同时锻炼静态与动态平衡能力。因此，有必要在前期研究的基础上，进一步开展静态与动态平衡能力相关关系的研究。

对老年人踝关节策略静态平衡和动态平衡进行Pearson 积差相关分析结果表明，老年人静态得分以及不同站立状态下的静态得分与动态得分的相关系数均不具有统计学意义（P＞0.05），说明老年人静态平衡能力与动态平衡能力总体上不存在相关性。人体静止站立时，足底压力中心始终在绕自己的平衡点不断晃动，这种晃动是自然的、不随意的，被称为生理性姿势动摇[16-17]。动摇的幅度和速度越大说明静态平衡能力越差。老年人通过踝关节维持静态平衡能力时，踝关节角度变化很小，生理性姿势动摇主要反映了踝关节周围的主动肌与拮抗肌、协同肌、固定肌之间的协调性，以及神经对肌肉的细微调控能力。本研究中所测试的动态平衡能力属于自动态平衡能力，即人体在进行各种自主运动或姿势转换时能重新获得稳定状态的能力[8]。老年人通过踝关节维持动态平衡能力时，由于平衡板极不稳定，踝关节的角度变化较大时才能维持身体平衡。因此，本研究中的动态平衡能力主要反映了老年人踝关节周围的主动肌与拮抗肌、协同肌、固定肌之间的协调性，以及神经对肌肉的粗大调控能力。综合以上分析，静态平衡能力和动态平衡能力需要神经对肌肉不同的调控能力，前者需要神经对肌肉的细微调控能力，后者需要神经对肌肉的粗大调控能力，这可能是造成老年人静态平衡能力与动态平衡能力总体上不存在相关性的主要原因。

由于维持老年人踝关节策略静态平衡能力与动态平衡能力的神经、肌肉、关节、韧带等组织都相同，老年人踝关节策略静态平衡与动态平衡间可能会存在内部联系。为探索这种内部联系，本研究采用因子分析法对静、动态平衡能力指标进行筛选、提取公因子，对公因子载荷较大的指标形成“指标集”，通过“指标集”间的典型相关分析探索静态与动态平衡的相关性。因子分析结果表明，双足睁眼、双足闭眼、线性步睁眼、单足睁眼分别为4个静态平衡公因子，包含指标都是轨迹长、包络面积和单位面积轨迹长；动态平衡共1个公因子，包含指标为中心区、垂直中、水平中和旋转速度。

本研究在因子分析中还验证了各指标对平衡能力贡献的方向。根据公因子载荷（见表4），动态平衡公因子中，中心区（Center）、垂直中（HM）和水平中（VM）3 个指标的因子载荷为正值，说明目标球在中心区、水平方向和垂直方向中间区域停留的时间越长，动态平衡能力越好。旋转速度的载荷为负值，说明旋转速度越小，动态平衡能力越好。静态平衡能力共提取了4 个公因子，轨迹长、包络面积的因子载荷均为负值，说明其值越小，静态平衡能力越好；单位面积轨迹长的因子载荷均为正值，说明其值越大，静态平衡能力越好。

以公因子包含的指标为指标集进行典型相关分析表明，老年人踝关节策略动态平衡能力与双足睁眼、单足睁眼状态的静态平衡能力相关系数均不具有统计学意义（P＞0.05）。但是典型相关分析表明，由中心区、垂直中、水平中、旋转速度组成的动态平衡，与由轨迹长、包络面积、单位面积轨迹长组成的双足闭眼、线性步睁眼静态平衡的典型相关系数均具有统计学意义（P＜0.05），且相关性较高。说明老年人踝关节策略静态平衡与动态平衡间确实存在内部联系。

本研究中的典型相关分析结果与Pearson 积差相关分析结果并不矛盾，前者对后者起到了补充作用。Pearson积差相关分析的变量为静态综合得分、4 种站立状态的静态得分和动态得分。这些“得分”均是平衡能力测试仪对人静态或动态平衡能力的总体评价，事实上损失了很多有价值的信息。如本研究采用的静态平衡能力测试仪，主要依据不同站立状态时的轨迹长进行评价计分，各站立状态静态平衡得分的均值为静态综合得分，用于对人体静态平衡能力进行最终评价。而轨迹长并不能全面评价人的静态平衡能力，常用于评价人体静态平衡能力的指标还有包络面积和单位面积轨迹长等[17-18]。本研究采用的动态平衡能力测试仪，主要依据目标球在各区域停留的时间百分比计算动态平衡得分，据此评价人的动态平衡能力，但是没有考虑到踏板的旋转速度。典型相关分析是从两变量集中分别提取有代表性的信息形成典型变量（分别为两变量集中各指标的线性组合），利用两典型变量之间的相关关系反映两变量集之间的整体相关性。因此，典型相关分析考虑的指标较多，其结果更具综合性，对Pearson积差相关分析具有补充作用。

典型变量的标准化换算系数、典型载荷和交叉载荷可以进一步反应动态平衡与静态平衡存在的内部联系。动态与双闭静态和线睁静态的典型相关分析显示，对各典型变量贡献较高的指标具有一定的差异性。但是，总体而言，在动态平衡与双足闭眼和线性步睁眼静态平衡的典型相关中，对动态平衡贡献较大的指标是Center 和HM，对双足闭眼和线性步睁眼静态平衡贡献较大的指标是Lng和Area（见表7）。

典型载荷结果显示（见表8），动态与双闭静态典型相关分析的第1 对典型变量中，Center、HM 和VM，与表示动态平衡的典型变量U1 具有负相关关系，Rot.speed 与U1 具有正相关关系，所以，此处U1 为“低优指标”，U1 越小，动态平衡能力就越好；Lng 和Area 与表示静态平衡的典型变量V1 具有负相关关系，Lng/A与V1几乎没有相关性，所以，此处V1为“高优指标”，V1 越大，静态平衡能力就越好。U1 与V1 的典型相关系数为0.812，结合前面因子分析验证的各指标对平衡能力贡献的方向可知，主要代表Center、HM 的动态平衡成分与主要代表Area、Lne/A的静态平衡成分具有较高的负相关关系（r=-0.812）（见表5）。具体判断过程见图3。

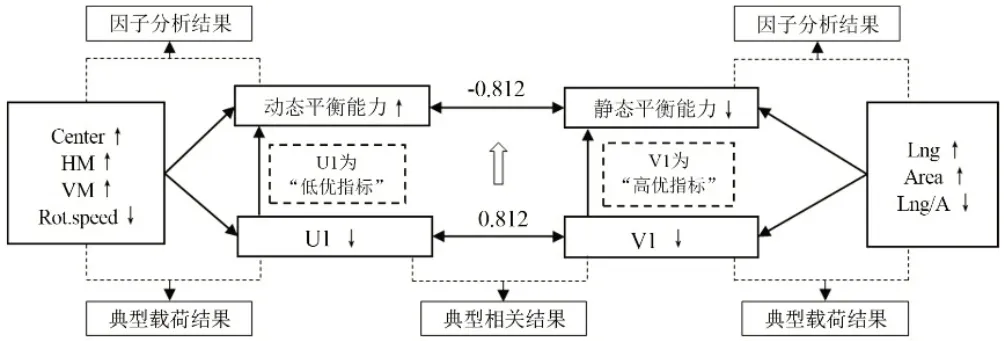
图3 基于U1和V1的静态与动态平衡能力相关关系判断过程图Figure3 Judging Process Diagram of Correlation Between Static and Dynamic Balance Capabilities Based on U1 and V1

同理，U2 与V2 的典型相关系数为0.607，主要代表HM、Center 的动态平衡成分与主要代表Lng、Area 的静态平衡成分具有中等的负相关关系（r=-0.607）。以此类推，动态与线睁静态典型相关分析中，主要代表HM、Rot.speed的动态平衡成分与主要代表Area、Lne/A 的静态平衡成分具有较高的正相关关系（r=0.790）。主要代表Center、VM 的动态平衡成分与主要代表Lng、Area 的静态平衡成分具有中等的负相关关系（r=-0.664）。动态与双闭静态和线睁静态典型相关分析中，第1 对典型变量的特征值远大于第2 对，所以动态平衡与静态平衡的内部联系主要体现在第1对典型变量之间的联系（见表5）。

交叉载荷结果显示（见表9），动态与双闭静态典型相关分析中，HM可以由主要代表Area、Lne/A的静态平衡典型变量V1预测，Lng 和Area 可以由主要代表Center、HM 的动态平衡典型变量U1预测，Lng/A可以由主要代表HM、Center的动态平衡典型变量U2预测，相关系数分别为-0.506、-0.715、-0.748和-0.518，决定系数分别为0.26、0.51、0.56和0.27。可见，中间2个指标的预测效果较好，其余2个指标预测效果一般。

动态与双闭静态典型相关分析中，Rot.speed可以由主要代表Area、Lne/A的静态平衡典型变量V1预测，Lng/A可以由主要代表HM、Rot.speed 的动态平衡典型变量U1 预测，Center 可以由主要代表Lng、Area 的静态平衡典型变量V2 预测，相关系数分别为0.598、-0.552 和0.610，决定系数分别为0.36、0.30 和0.37。可见，预测效果均一般。

4 结 论

老年人踝关节策略静态平衡能力与动态平衡能力不存在相关性，但是静态平衡与动态平衡间存在内部联系。这种联系主要表现在：主要代表Center、HM的动态平衡成分与主要代表Area、Lne/A 的静态平衡成分具有较高的负相关关系（r=-0.812）；主要代表HM、Rot.speed的动态平衡成分与主要代表Area、Lne/A 的静态平衡成分具有较高的正相关关系（r=0.790）；主要代表Center、HM的动态平衡典型变量U1，对双足闭眼静态平衡中的指标Lng和Area的预测效果较好。