对一道填空压轴题的思考

范建兵

一、例题呈现

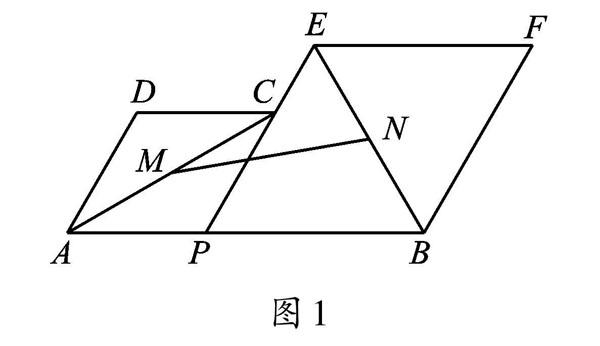
（2018年江苏省苏州市中考试卷第18题）如图1，已知AB=8，P为线段AB上的一个动点，分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE，点P、C、E在一条直线上，∠DAP=60°。M、N分别是对角线AC、BE的中点。当点P在线段AB上移动时，点M、N之间的距离最短为____（结果保留根号）

二、图形识别

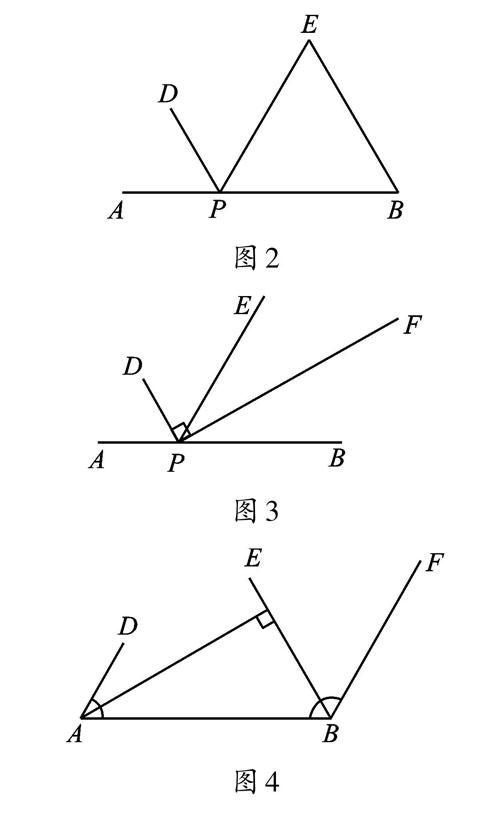
几何问题的解决常常需要把握两个关键：一是识别几何图形，二是寻找分析思路。对于复杂的几何图形，同学们常常不知道从哪里入手，此时较好的解题策略就是图形分解，即从原有的复杂图形去寻找，并拆分出若干个基本图形，呈现出我们学习过程中比较熟悉的教材经典模型。在这道压轴题的图形中，除了等边三角形、菱形、等腰三角形、线段中点等基础图形，可能还隐含了一些常用的组合图形：图2表示的是“等腰三角形+顶角外角平分线”模型;图3表示的是“互为邻补角的两个角的角平分线互相垂直”;图4表示的是“平行线中一组同旁内角的角平分线互相垂直”;图5表示的是“线段PQ是定点Q与直线AB上的动点P之间的最小值”。这四个基本图形都是几何学习中常见的图形，个个经典但深藏于本题之中，只要我们善于观察、思考、分析图形，找出这些基本图形，及时关联思考，就一定会找到解决问题的方法。

三、思路分析

在基本图形识别清楚后，我们再回头分析例题，分析已知条件与所求问题，由已知想所求，抽丝剥茧，并有针对性地进行思考。

问题1，题中要求点M、N之间的最短距离，我们可以从几个角度进行思考：

1点M和点N是动点还是定点？（是动点。）

2运动过程中，两点的运动路径是什么样的？（先寻找两个动点的特殊运动状态，如起点、终点、过程中任一点等。）

3线段MN什么时候最短？（线段最短的依据有两个：一是两点之间线段最短，另一个是垂线段最短。本题中属于哪一种情况呢？）

问题2，菱形、等边三角形有什么作用？

本题中如何运用特殊图形的性质？题中还隐含了等腰三角形，还有30度的角，这些隐含条件能不能为解题发挥作用？两个动点与这些特殊圖形有什么关联？

问题3，已知中只有一个数量关系，即AB=8，题中的线段哪些是定量？哪些可变？如何表示变量与所求线段MN的关系？

四、解法呈现

解法一：如图6，连接DP、PF，尽管点P是动点，但在运动过程中一直有如下两个结论：1点M恰好是线段DP的中点，点N恰好是线段PF的中点;2∠MPN=90°。设AP=x，由直角三角形中30°角的性质及

解法二：如图7，连接DP、PF、DF，图中存在两个结论：1点M恰好是线段DP的中点，点N恰好是线段PF的中点;2∠MPN=90°。设AP=x，由直角三角形中30°角的性质及勾股定理可得，PB=8-x，DP=x，PF=3（8-x），所以DF=x2+[3（8-x）]2=4x2-48x+192=4（x-6）2+48，所以当x=6时，DF取得最小值为43，由三角形中位线可得MN的最小值为23。

解法三：如图8，设直线AC与直线BE交于点Q，由题意得，△AQB是直角三角形且∠QAB=30°，所以无论动点P如何运动，点Q及△AQB都唯一确定。由于矩形MPNQ对角线相等，即MN=PQ，因此求MN的最小值问题就转化为求PQ的最小值。如图9，当QP⊥AB时，PQ取得最小值23，因此MN的最小值为23。

五、变式巩固

解题之后我们还需要有一定的反思及巩固，以加强对这类题目的理解，可以反思：这类题还可以怎么做？这类题为什么可以这么做？这些方法中哪种方法更简便？等等。还可以反思题目的变式，将原题的条件或结论变一变、改一改，重新设计问题，以考验我们对知识的理解掌握和融合变化的能力。比如这一题，从简化图形这个角度，我们可以变出如下问题。

变式1：如图10，线段AB=8，点P为线段AB上一动点，分别以AP、PB为边，在AB同一侧作等边△APD和等边△PBE，M、N分别是DP、BE的中点。当点P在线段AB上移动时，求MN的最小值。

变式2：如图11，线段AB=8，点P为线段AB上一动点，∠A=60°，PA=PC，PB=PE，点M、N分别是AC、BE的中点。当点P在线段AB上移动时，求MN的最小值。

变式3：如图12，线段AB=8，点P为线段AB上一动点，分别以AP、PB为直径画圆，D、E分别为两圆上的点，且∠DAB=60°，AD∥EP，连接DE，求DE的最小值。

以上三个变式题与原题相比，形变但质不变，内涵不变，思路不变，方法不变，这样的变化与思考更能体现学一题、会一类的解题效果。

（作者单位：江苏省苏州学府中学校）