构造辅助圆 巧求最小值
吴玲芳


在求平面几何中的一些线段的最小值时,我们通常作辅助线来求解。例如“将军饮马”这类问题,可以作对称点,利用轴对称的知识帮助解决。而有些求线段的最小值的问题,用常规的解题方法难以求解。此时,我们可以从已知条件出发,根据圆的定义,或利用圆周角定理及其推论,构造辅助圆,运用圆的知识进行解答,从而求出线段的最小值。
一、从定长入手构造圆
例1如图1,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是BC边上的动点,将△EFB沿EF所在的直线折叠得到△EB′F,连接B′D,则B′D的最小值为。
【分析】折叠过程中,B′E=BE,所以B′E的长度不变,即动点B′到定点E的距离是一个定值,所以点B′的运动轨迹是以点E为圆心,2为半径的圆的一部分,以此构造辅助圆(如图2)。B′D的最小值就是点D与圆E上的点的最短距离,当点D、E、B′三点共线时(如图3),B′D最短。
解:如图3,∵四边形ABCD是矩形,
∴∠DAB=90°。
∵在Rt△ADE中,AE2+AD2=DE2,
又∵AE=2,AD=6,
∴DE=210。
当点D、E、B三点共线时,DB'最短。
∵BE=BE=2,
∴DB'=210-2。
【点评】圆的集合定义是到定点的距离等于定长的点的集合。在本题中,折叠只改变图形的位置,不改变图形的形状。无论折到什么位置,B'E的长度始终保持不变,所以可以构造辅助圆来解决问题。审题的关键是找到一条长度确定的线段,一个端点是定点,另一个端点为动点,那么动点的运动轨迹是圆。
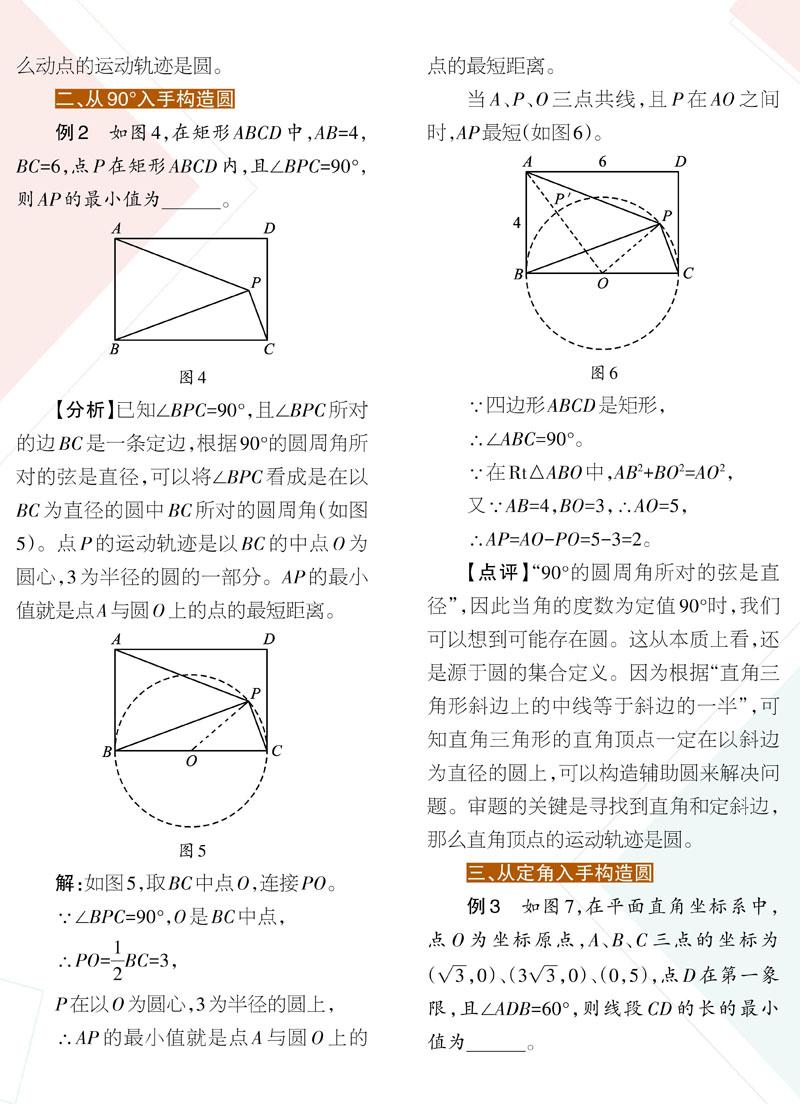
例2如图4,在矩形ABCD中,AB=4,BC=6,点P在矩形ABCD内,且∠BPC=90°,则AP的最小值为。
【分析】已知∠BPC=90°,且∠BPC所对
的边BC是一条定边,根据90°的圆周角所对的弦是直径,可以将∠BPC看成是在以BC为直径的圆中BC所对的圆周角(如图5)。点P的运动轨迹是以BC的中点O为圆心,3为半径的圆的一部分。AP的最小值就是点A与圆O上的点的最短距离。
解:如图5,取BC中点O,连接PO。
∵∠BPC=90°,O是BC中点,1
∴PO=2BC=3,
P在以O为圆心,3为半径的圆上,
∴AP的最小值就是点A与圆O上的点的最短距离。当A、P、O三点共线,且P在AO之间
时,AP最短(如图6)。
∵四边形ABCD是矩形,
∴∠ABC=90°。
∵在Rt△ABO中,AB2+BO2=AO2,
又∵AB=4,BO=3,∴AO=5,
∴AP=AO-PO=5-3=2。
【点评】“90°的圆周角所对的弦是直径”,因此当角的度数为定值90°时,我们可以想到可能存在圆。这从本质上看,还是源于圆的集合定义。因为根据“直角三角形斜边上的中线等于斜边的一半”,可知直角三角形的直角顶点一定在以斜边为直径的圆上,可以构造辅助圆来解决问题。审题的关键是寻找到直角和定斜边,那么直角顶点的运动轨迹是圆。
例3如图7,在平面直角坐标系中,点O为坐标原点,A、B、C三点的坐标为(3,0)、(33,0)、(0,5),点D在第一象限,且∠ADB=60°,则线段CD的长的最小值为。
【分析】因为∠ADB=60°,且∠ADB所对的边AB是一条定边,根据“同弧所对的圆周角相等”,可以将∠ADB看成是在以AB为弦的圆M中AB所对的圆周角(如图8)。点D的运动轨迹是圆M的一部分,CD的最小值就是点C与圆M上的点的最小距离。CD的最小值=CM-r,r是圆M的半径。
解:设∠ADB所在的圆的圆心为点M,根据同弧所对的圆周角是其所对圆心角的一半,可知∠AMB=120°。
过点M作MH⊥x轴于点H,由垂径定理可知∠AMH=12∠AMB=60°。
∵A(3,0)、B(33,0),
∴AB=23。
在Rt△AMH中,AH=3,∠AMH=60°,可得MH=1,AM=2,即r=2。当点C、M、D三点共线,且D在CM之间时(如图9),CD的长度最短。
过M作MN⊥y轴于点N。
∵在Rt△CNM中,CM2=CN2+NM2,
又∵CN=CO-NO=CO-MH=5-1=4,NM=OH=OA+AH=23,
∴CM=27,
∴CD的最小值为CM-r=27-2。
【点评】当角的度数确定,角所对的边是一条定边,根据“同弧所对的圆周角相等”,那么角的顶点的运动轨迹是圆。此时,角可以看成圆周角,定边是圆的一条弦,先利用同弧所对的圆周角是其所对的圆心角的一半,找到圆心的位置,再确定圆的半径,最终构造出辅助圆。审題的关键是找到有特殊角度的角,且角的对边是一定边,那么该角的顶点的运动轨迹是圆。当角的度数是90°时,其实是这类情形中的特殊情况,比如例2。
(作者单位:江苏省常州外国语学校)

