基于几何模型的初中数学教学设计与反思
——以一道中考题复习教学为例
广东省广州市铁一中学(511400) 马小飞
1 题目呈现
(2018 广州第23 题)如图1,在四边形ABCD中,∠B=∠C=90◦,AB >CD,AD=AB+CD.(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法).(2)在(1)的条件下.

图1
①证明:AE ⊥DE.
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
2 设计依据
2.1 考试依据
(改编自新人教版八上教材第52 页第7 题) 如图1,∠B=∠C=90◦,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
对比分析:2018年中考将教材中条件“E是BC的中点”改变为“AD=AB+CD”;将“DE平分∠ADC”改成尺规作图;将求证内容“AE是∠DAB的平分线”变为更深层次的考查.
2.2 考点依据
本题是融合了四大核心素养(空间观念、推理能力、应用意识、创新意识)于一体的综合问题.
本题考查了尺规作图、角平分线性质、全等三角形的判定与性质、矩形的判定与性质、轴对称的应用——最短距离问题(将军饮马与垂线段最短结合)、相似三角形的判定与性质.
2.3 学情依据
初三学生已学过一些几何模型,比如角平分线模型、截长补短模型、三垂直模型等,但对几何模型的认识还停留在比较浅的层次,对几何模型应用还不够灵活和深入.部分学生对几何模型的特征和作用还不够熟悉,遇到综合题不会见条件联想辅助线,更不会创新应用几何模型.
2.4 理论依据与设计思路
布鲁纳认为,个体认知结构的发展与获得是凭借三种不同的表征形式:动作性表征、图象性表征、符号性表征[1].这三者之间相互联系,相互影响.
根据布鲁纳理论,笔者将几何模型视为图象性表征,几何语言是为符号性表征,思维流程图视为动作性表征,利用思维流程图将几何模型和几何语言联系起来,培养学生从题目条件和直观图形中进行思考,利用几何模型将条件有机结合起来,从而找到突破口,再转化成几何语言.
笔者通过一个直角梯形贯穿整个教学设计,利用熟悉的图形,不同的条件,产生不同的解法,通过一图多变,一题多解,一解多用,梳理几何模型,引导学生从题中条件或所求的结论中发现几何模型的影子,利用几何模型的特征和作用来添加辅助线,形成几何问题模型化思维,培养学生转化问题的能力,迁移知识的能力,以及应用和创新意识.
3 教学过程
3.1 问题引入,揭示课题
课件展示:2018 广州第23 题(如前面题目呈现)
设计意图通过直观题展示让学生感受教材与中考的关系,及教材题型的深度和广度,让学生关注中考动向,认识到几何模型的重要性.
3.2 自主探究,解决问题
例1(选自2018 广州第23 题第(2)1①)如图2,在四边形ABCD中,∠B=∠C=90◦,AB >CD,AD=AB+CD,作DE平 分∠ADC,连接AE.证明:AE ⊥DE.
疑难点分析:由“角平分线”想“垂线”,或由“线段和差”想“截长补短”,或由“平行+角平分线”想“等腰三角形”.

图2
教师启发提问1:如何理解AD=AB+CD?
口诀:遇线段和差联想截长补短模型.
教师启发提问2:如何利用条件DE平分∠ADC?
口诀:遇角平分线向两边作垂线.
思维流程图:

设计意图通过自主探究,教师启发学生突破解题难点,合理猜想,寻思路,培养学生见条件想方法或模型的解题思路.
3.3 开放探究,深层挖掘
思考:如图3,针对上述证法图形,你还可以得到哪些结论?比一比,看谁写的多!

图3
①___
②___
③___
④___
⑤___
……
疑难点分析:根据题中的线角特征,发挥想象力,从不同角度思考条件和结论.
设计意图在例1 的基础上进一步引发思考,设置开放性结论探索题,提升学生的求知欲、探索欲,培养学生从不同角度思考条件和结论,从而进行创新思考,而不是做一题解一题,更多的是明白一个题目背后隐藏的深层次问题和结论.同时为下一个问题做好铺垫,从而培养学生从复杂的图形中分离不同的几何模型,提升空间观念、推理能力、创新意识等核心素养.
3.4 变式应用,突破自我
结合上述思考中的条件和多种结论,改变题中的条件结论,促使学生进行灵活应用.
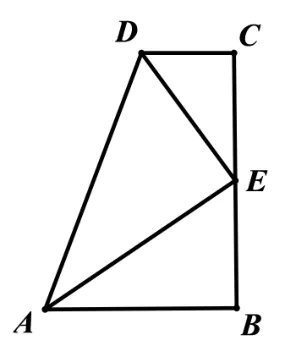
图4
变 式1(自 编):如 图4,∠B=∠C=∠DEF=90◦,E是BC的中点.求证:AD=AB+CD.
疑难点分析:遇“线段和差”考虑“截长补短”,利用分段相等来证明.或遇“中点”考虑“倍长线段”.
思维流程图:

设计意图变式1 将条件设置为三个直角和中点条件不变,从中点和所求联想倍长模型和截长补短模型,进行拓展应用,培养学生学会审题,辨识题中条件和结论的特点,从而发现对应的几何模型,学会添加辅助线.
变式2(自编):如图5,∠B=∠C=∠DEF=90◦,E是BC的 中 点.求 证:AE平 分∠DAB.
疑难点分析:“由三垂直想相似”,或“遇中点可倍长线段”构造全等.
思维流程图:
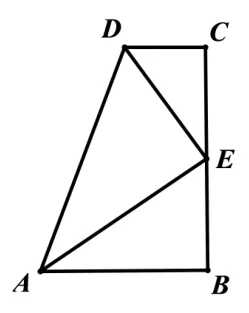
图5

设计意图变式2 是在变式1 的基础上改变求证结论,培养从不同角度来思考题中呈现的条件和结论.变式2 与变式1 有相同的证法,却又有变式2 的独特证法(即利用三垂直模型中的相似来证).
变式3:(八年级期末复习卷) 如图6,已知BC > AB,AD=DC,BD平分∠ABC,求证:∠A+∠C=180◦.
疑难点分析:有线段和角相等作条件证明两角互补,考虑构造全等,遇“角平分线”作“垂线”.
思维流程图:

图6

设计意图变式3 是将直角梯形化为普通四边形,再次加深对角平分线的特征认识.角平分线是轴对称图形,由该对称性可以引发多种思考.
3.5 梳理总结,画龙点睛
梳理本节所涉及的几何模型:

模型一:角平分线模型:模型二:截长补短模型:口诀:遇角平分线作垂线)口诀:遇线段和差想截长补短)作用:证线段相等作用:构造全等images/BZ_35_269_1547_609_1719.pngimages/BZ_35_729_1565_1209_1719.png(截长)(补短)(补短)模型三:中心对称模型:模型四:平行线+角平分线口诀:遇中点倍长线段⇒等腰三角形作用:构造全等images/BZ_35_269_1951_684_2141.pngimages/BZ_35_729_1961_1157_2141.png模型五:三垂直模型⇒相似模型六:隐圆模型⇒由EB=EC=EF产生images/BZ_35_269_2267_452_2470.pngimages/BZ_35_729_2267_957_2470.png模型七:筝形:(筝形是轴对称图模型八:射影定理模型(即双垂直模型)B形,蕴含点与点F关于AE对称或AE垂直平分BF,该模型包含角平分线模型)images/BZ_35_269_2754_609_2905.pngimages/BZ_35_729_2703_912_2905.png
3.6 中考链接
练习1(2018• 娄底) 如图7,已知半圆O与四边形ABCD的边AD、AB、BC都相切,切点分别为D、E、C,半径OC=1,则AE·BE=____.
练习2(2016• 广州) 如图8,点C为∆ABD外接圆上的一动点(点C不在弧BAD上,且不与点B,D重合),∠ACB=∠ABD=45◦.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:;

图7
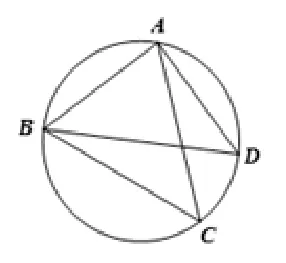
图8

图9
(3)若∆ABC关于直线AB的对称图形为∆ABM,连接DM,试探究DM2,AM2,BM2三者之间满足的等量关系,并证明你的结论.
练习3(2019•广州)如图9,等边∆ABC中,AB=6,点D在BC上,BD=4.点E为边AC上一动点(不与点C重合),∆CDE关于DE对称的图形为∆FDE.
(1)当点F在AC上时,求证:DF//AB;
(2)设∆ACD的面积为S1,∆ABF的面积为S2,记S=S1−S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;
(3)当B,F,E三点共线时,求AE的长.
4 教学反思
4.1 设计思维流程图,突出核心破题思路
通过思维流程图,将解题思路清晰化,突出破题思路,抓住关键的破题口,利用几何模型穿针引线,加上口诀,强化学生的几何模型思维,进一步加深对几何模型的认识,熟悉几何模型的特点和作用.
4.2 开放探究,培养多角度几何模型思维
通过思考栏目,从例1到思考,结合学生的认知结构,构建新的知识结构,发散学生思维,将学生想象空间放大,游走于各种几何模型的特点之间,产生多种多样的几何结论.这其实正是学生对几何模型的图象性表征、符号语言表征与动作性表征之间的转化.
4.3 变式应用,培养几何模型的应用能力
通过自编题来加强学生的应用能力,同时也是对所学的一种考查,变式图形变化不大,条件略微改变,能够激发学生对条件的认识,对突破口的找寻又多了一些方法,思维灵活度变强,发展学生的创造力,使学生在动作性表征上得到了进一步发展.
4.4 中考链接,培养综合应用能力
通过中考真题,将图形条件复杂化,已知条件淡化,培养学生从错综复杂的题目中寻找,并联想几何模型,找出跟几何模型有关联的条件,即找出解题突破口,从而加强学生的综合应用能力,可以说学生在图象性表征、符号语言表征与动作性表征上,又是一次提高.
4.5 初中数学几何模型教学的衔接与反思
结合初中三年的课本,笔者发现大部分几何模型都由轴对称统领.这些几何模型是由课本的几何定理衍生出来的,与教材是息息相关的.而“轴对称”是人教版八年级上册第十三章内容,是安排在基本的平面几何图形之后,包括线段、角、平行线、三角形、角平分线,这些图形本身就是轴对称的特点,在学生初步直观感受之后,课本在八年级上册对轴对称的概念进行了系统的提出,轴对称概念的出现可以说是起着承上启下的作用.也就是说课本是从等腰三角形才开始正式用轴对称的观点来引入平面几何图形.轴对称是一种特殊的图形的特点,它几乎贯穿于之后的所有几何图形中,比如垂直平分线、等腰三角形、等腰直角三角形、矩形、菱形、正方形、圆,甚至于代数问题中的抛物线、双曲线都是轴对称图形,可以说轴对称是平面几何图形的鼻祖.
笔者从轴对称的角度研究发现,轴对称在课本的概念、习题、数学活动中均有渗透,因此,在几何教学中,教师应该从初一开始就渗透轴对称的特征,随着新知识的增加,逐步地整理、归纳、提升,建立一个立足于轴对称的知识网络,使知识点间的特点鲜活起来,统一起来,让学生更容易联想和应用.
轴对称,从基础操作来说就是折叠与重合产生的,教师的教学可以从折叠开始引入.笔者在研究教材时发现,在认识线段时,课本的引例就是从折叠开始的,那么为人师者应该从较高的思想角度来渗透轴对称的概念,从而更好地引入几何概念,在几何教学中把握住轴对称的精髓,通过无形的渗透,提升中学生几何素养.比如,在引入“线段的中点”时,教材中黄色框提醒通过折叠可以找到线段的中点,这其实就是轴对称的渗透.笔者在教学时改编了一下,利用一根绳子引入,让同学们想办法做成两根鞋带,学生很快通过对折找到绳子的中点.又如在角平分线的引入后,课本通过折纸作角平分线.又如人教版七年级上册课本第149 页习题第12题,课本第144 页数学活动折五角星,这些活动背景均跟折纸有关,而折纸又是轴对称的基本雏形,可以说折叠是引入轴对称图形的基本方法.再如2019年广州中考第24 题的图形背景也是折叠.因此,笔者认为有必要以折叠的思想统领初中几何与轴对称有关的知识.

