高一数学测试

一、单选题(本大题共12小题，每小题5分，计60分)

1.设在∆ABC中,角A,B,C所对的边分别为a,b,c, 若bcosC+ccosB=asinA, 则∆ABC的形状为 ( )

(A)锐角三角形 (B)直角三角形

(C)钝角三角形 (D)不确定

2.在∆ABC中,角A,B,C所对的边分别为a,b,c,bcosC=a,点M在线段AB上,且∠ACM=∠BCM.若b=6CM=6,则cos∠BCM=( )

3.直线l1:x+my+6=0和l2:(m-2)x+3y+2m=0互相平行,则m的值为( )

(A)-1或3 (B)3

(C)-1 (D)1或-3

4.如图,无人机在离地面高200 m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°.已知∠MCN=60°,则山的高度MN为( )

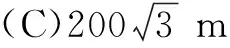
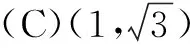
6.设入射光线沿直线y=2x+1射向直线y=x,则被y=x反射后,反射光线所在的直线方程是( )

(A)x-2y+3=0 (B)x-2y+1=0

(C)3x-2y+1=0 (D)x-2y-1=0

7.已知直线l1:ax+4y-2=0与直线l2:2x-5y+b=0互相垂直,垂足为(1,c),则a+b+c的值为( )

(A)20 (B)-4 (C)0 (D)24

8.已知直线y=2x是∆ABC中∠C的平分线所在的直线,若点A,B的坐标分别是(-4,2),(3,1),则点C的坐标为( )

(A)(-2,4) (B)(-2,-4)

(C)(2,4) (D)(2,-4)

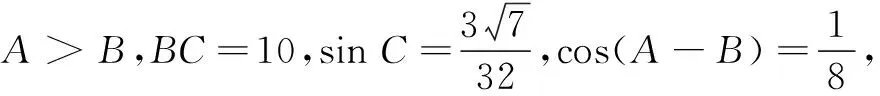
(A)[-5,5] (B)[-6,6]

(C)[-7,7] (D)[-8,8]

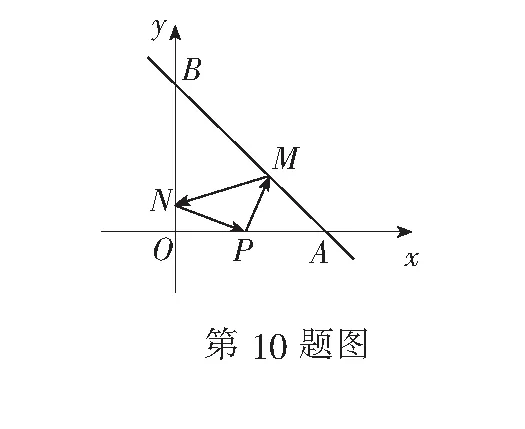
10.如图,已知A(4,0)，B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到点P,则光线所经过的路程是 ( )

11.已知点A(-2,0),B(2,0),C(1,1),D(-1,1),直线y=kx+m(k>0)将四边形ABCD分割为面积相等的两部分,则m的取值范围是( )

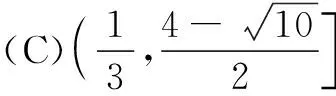
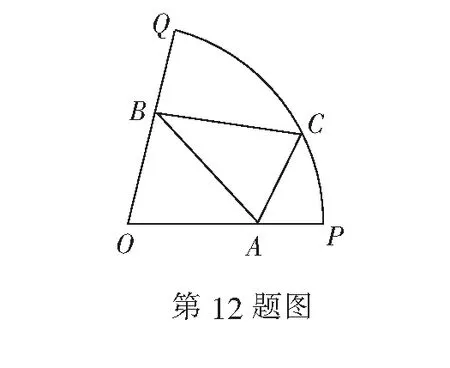
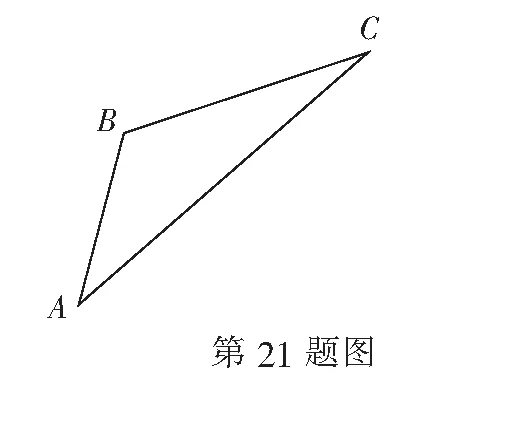
12.如图,已知OPQ是半径为2,圆心角为75°的扇形,点A,B,C分别是半径OP,OQ及扇形弧上的三个动点(不同于O,P,Q三点),则∆ABC周长的最小值是( )

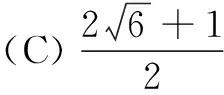
二、填空题(本大题共4小题，每小题5分，计20分)

13.已知直线l过点P(-1，2)，且与以A(-2,-3),B(3,0)为端点的线段AB相交,则直线l斜率的取值范围______.

14.将一张坐标纸折叠一次,使点(10,0)与点(-6,8)重合,则与点(-4,2)重合的点是______.

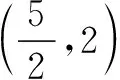
三、解答题(本大题共6小题，计70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知直线l:x+2y-2=0.试求:

(1)点P(-2,-1)关于l的对称点坐标;

(2)直线l关于点(1,1)对称的直线方程.

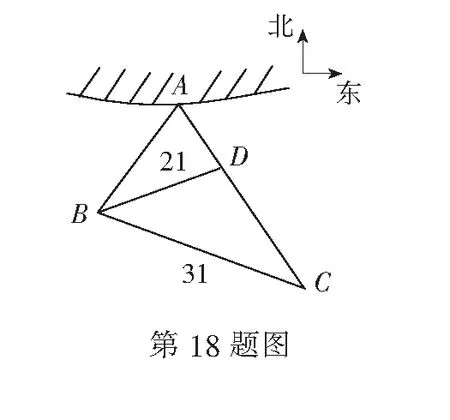
18.(本小题满分10分)如图所示,近日我渔船编队在岛A周围海域作业,在岛A的南偏西20°方向有一个海面观测站B,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与B相距31海里的C处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛A直线航行以保护我渔船编队,30分钟后到达D处,此时观测站测得B,D间的距离为21海里.

(1)求sin∠BDC的值;

(2)试问海警船再向前航行多少分钟方可到岛A?

19.(本小题满分10分)在∆ABC中,内角A,B,C所对的边分别为a,b,c,且

(2b-3c)cosA+2acosB=0.

(1)求cosA的值;

(2)若a=3,b+c=5,求∆ABC的面积.

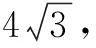
(2)若∆ABC是锐角三角形,求∆ABC周长的取值范围.

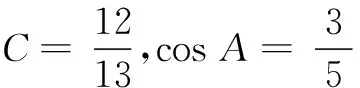
(1)求索道AB的长;

(2)当乙在缆车上与甲的距离最短时,乙出发了多少min?

(3)为使两位游客在C处互相等待的时间不超过3min,问乙步行的速度应控制在什么范围内?

22.(本小题满分16分)已知直线l:(2m+1)x+(m-1)y-5m-1=0,且l与坐标轴围成的三角形面积为S.

(1)求证:不论m为何值,直线l过定点P;

(2)分别求S=3和S=5时,所对应的直线条数;

(3)针对S的不同取值,讨论集合A={l|直线l经过点P,且l与坐标轴围成的三角形面积为S}中的元素个数.

参考答案

一、单选题

1.B；2.B；3.C；4.A；5.A；

6.D；7.B；8.C；9.D；10.D；

11.D；12.B.

二、填空题

14.(4,-2);15.(1,2)，32x-y+30=0;

三、解答题

17.(1)设所求对称点为P′(x0,y0),则

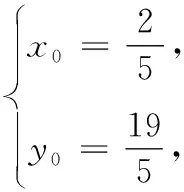
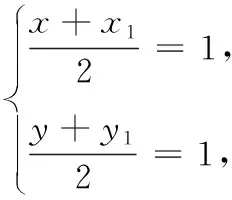
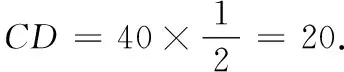
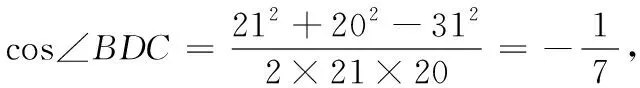
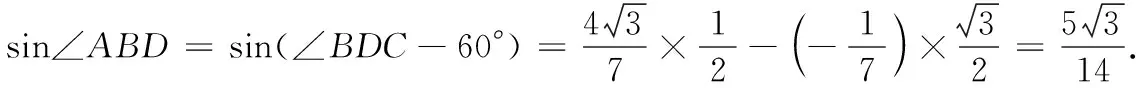
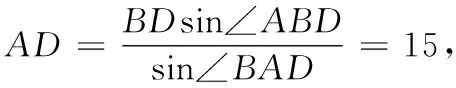
即海警船再向前航行22.5分钟即可到达岛A.

19.(1)由正弦定理，得(2sinB-3sinC)cosA+2sinAcosB=0,故2(sinAcosB+sinBcosA)=3sinCcosA,即2sin(A+B)=3sinCcosA.

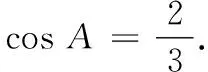
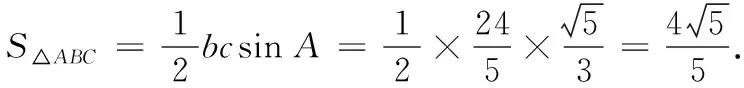
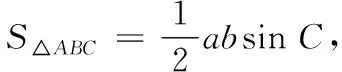
又由c2=a2+b2-2abcosC，得16=a2+b2-ab,即a2+b2=32.

联立方程组，可得a=b=4.故∆ABC为等边三角形.

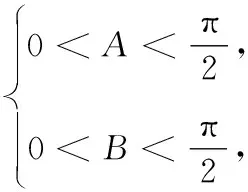
所以，∆ABC的周长为

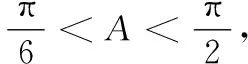
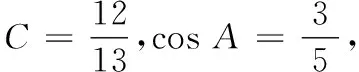
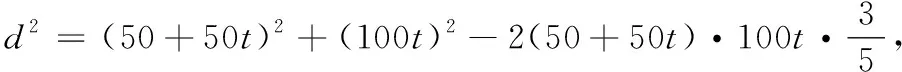
乙从B出发时,甲已经走了50(1+5+1)=350 m,还需走910 m才能到达C.

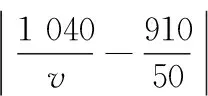
即乙步行的速度应控制在[49.1,68.4]范围内.

22.(1)已知直线方程可化为m(2x+y-5)+(x-y-1)=0.

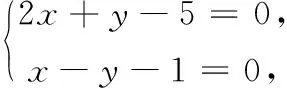
故不论m为何实数,直线l过定点P(2,1).

(2)由题意,直线的斜率k存在,且k≠0.

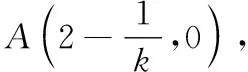
令S=3,得(2k-1)2=6|k|.

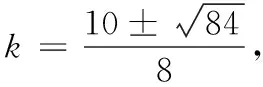
综上,S=3时，对应直线有两条.

令S=5,得(2k-1)2=10|k|.分k>0及k<0讨论，类似可得对应直线有四条.

(3)由题意,(2k-1)2=2S|k|.

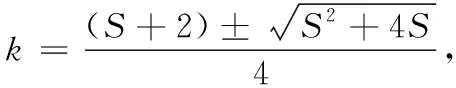
当k<0时,方程化为4k2-(4-2S)k+1=0,Δ=4S(S-4).

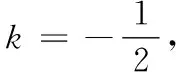
综上,04时有4条直线.即04时,集合A中的元素有4个.

的四个命题: ① |z|=2; ②z2=2i; ③z的共轭复数为1+i;④ 若|z0-z|=1,则