基于GSA-GA神经网络的铸造企业订单准入评价研究
唐红涛,方 博,高晓灵,李香怡,殷伟铭
(武汉理工大学 机电工程学院,湖北 武汉 430070)
本文研究对象是制造业中典型的砂型铸造企业,结合实际调研,砂型铸造企业的订单以单件小批量为主,订单类型多且复杂,每个订单的订货数量都很大。砂型铸造企业完成一个订单的加工需多部门共同协作,这增加了企业运作管理难度。每个订单的需求、交货期、生产成本、价值等都不一致,企业对每个客户的重视程度都不一致等因素增加了企业对一个生产周期内的所有订单进行精细生产计划安排的难度。企业如果不能针对现有的订单制定合适的生产计划,造成不能按时交付订单,将会减少企业的利润、增加库存成本、降低企业信誉等一系列后果。企业订单越多,就越能提升企业的销售额,但是企业的生产能力是有限的,应该按照利润、生成成本、客户重要度等因素建立订单准入评价体系,以此来指导企业对客户订单的选择与生产计划的制定。综合考虑多个现实因素建立订单准入评价体系也是本文需要重点研究的问题。
通过研究国内外学者对订单准入的评价,Kalantari等[1]基于模糊TOPSIS方法和混合整数数学规划模型,提出一种订单接受/拒绝决策支持系统。Akyildiz等[2]研究基于联合分析法的客户订单选择因素优先级排序。王晓欢等[3]提出基于SMART算法的最优订单接受策略求解方法。曹裕等[4]研究基于TOPSIS方法和MDP模型的分层MTO订单的准入策略。部分研究学者将订单准入评价与车间调度问题相结合。Zhong等[5]以最小化所有已接受订单的完工时间加上所有已拒绝/过期订单的总罚款为目标,建立一个带有机器可用性约束的订单接受和调度模型。Jiang等[6]研究由制造商和客户组成的供应链中批量交货的订单接受和调度问题,并提出两种近似算法进行研究。Esmaeilbeigi等[7]提出两种新的混合整数规划公式,用于求解两机加工车间的订货验收和调度问题。
本文在此基础上研究砂型铸造企业订单准入评价决策问题,并提出一种基于混合GSA-GA神经网络的砂型铸造企业订单准入评价决策模型。引力搜索算法(gravational search algorithm)是受物体间存在引力启发而提出的一种智能算法,一经提出就被广泛应用于各个领域,如控制工程[8]、土木工程[9]和工业管理[10]等领域。但是将GSA算法应用到砂型铸造领域的研究并不多。为弥补文献中这一缺陷,本文将其应用到砂型铸造企业订单准入评价决策模型中,且对基本GSA算法在前人的基础上进行改进[11-14]。为保证GSA算法随机初始化种群特征,引用Tent混沌映射进行初始化种群,为使算法能够跳出局部最优解和避免算法早熟收敛,采用基于遗传算法的交叉变异算子进行交叉变异操作,在神经网络迭代过程中使用Adam算法代替传统的随机梯度下降算法进行误差方向传播。最后通过现实企业实际案例来进行实例分析,验证本文所建立模型的适用性和算法的有效性。
1 砂型铸造企业订单准入评价指标体系设计
本文结合砂型铸造企业运作特点和实际调研,建立目标层、部门层、指标层的三级订单准入评价指标体系。目标层为订单的最终评价值;部门层分为商务部门、技术部门、生产部门、财务部门;指标层是以各个部门来确定的11个指标层。砂型铸造企业订单准入评价指标体系见表1。
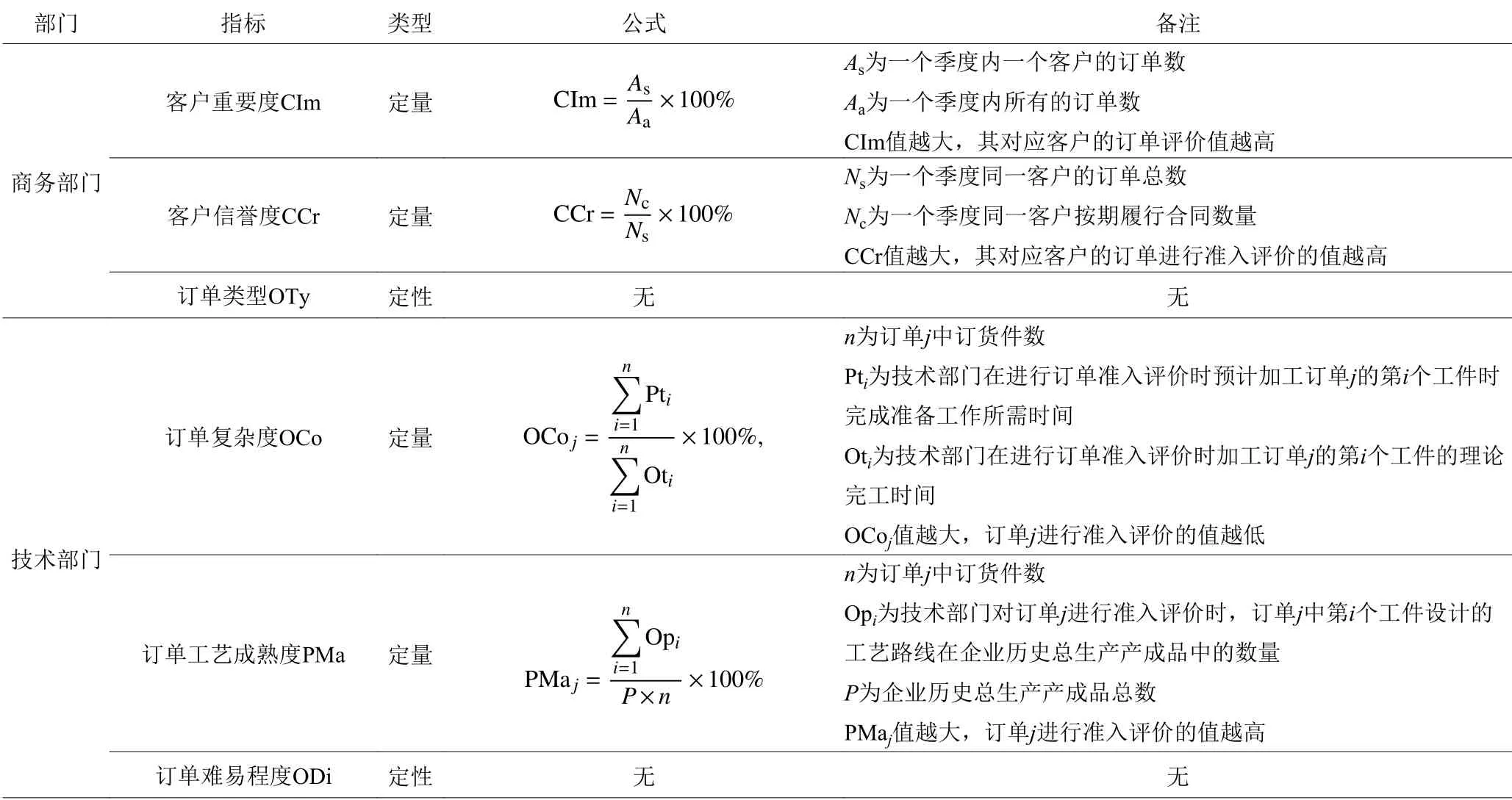
表 1 砂型铸造企业订单准入评价指标体系Table 1 Sand casting enterprise order acceptance evaluation index system
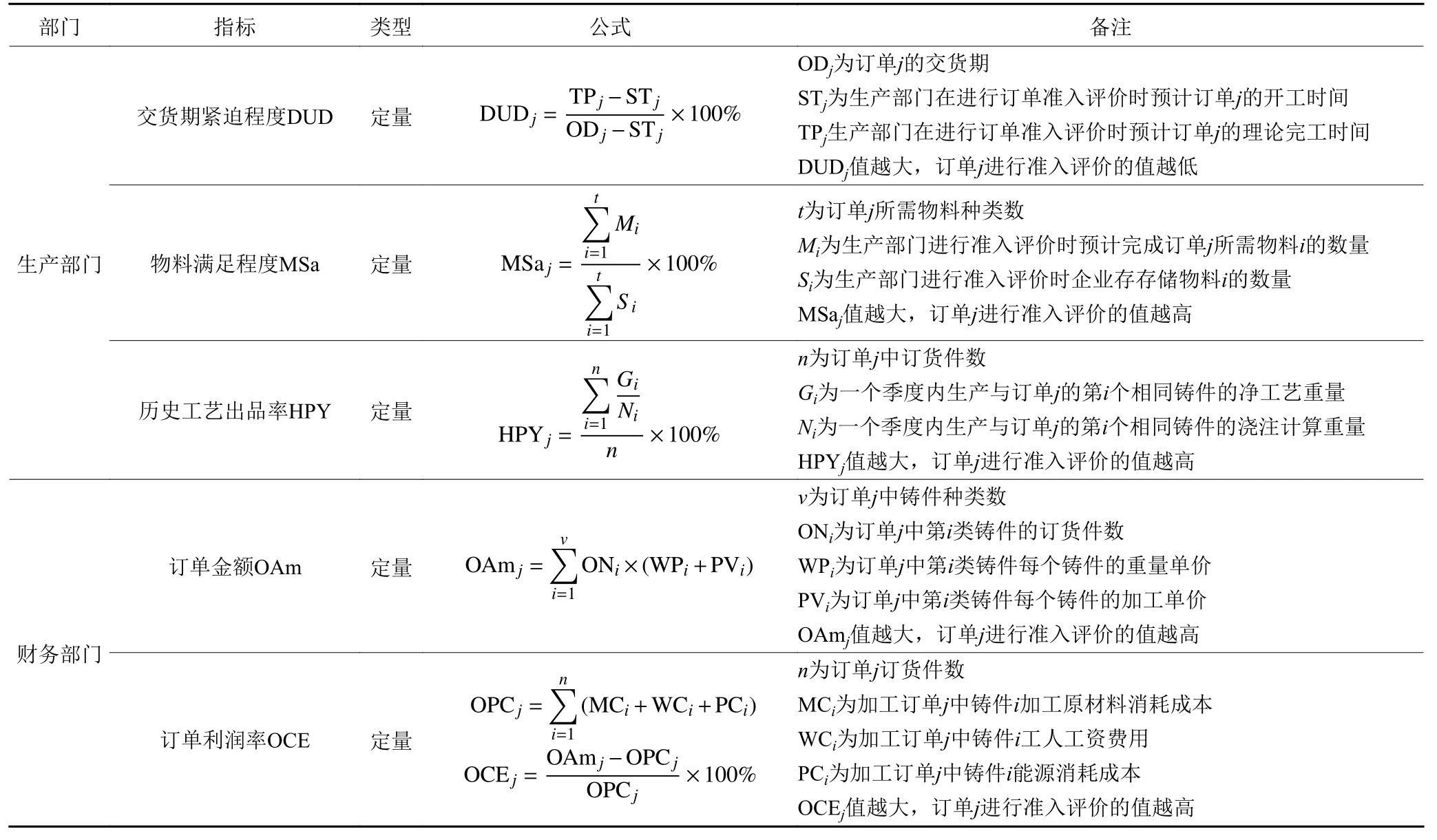
续表
本文对定性指标等级分数分为5类,如表2所示。
2 基于GSA-GA神经网络的订单准入评价模型构建
2.1 混合GSA-GA神经网络算法流程
本文基于混合GSA-GA神经网络算法对砂型铸造企业订单准入评价模型进行求解。算法主要结构包括数据处理、GSA-GA算法编码设计和确定参数、确定神经网络结构、GSA-GA全局优化、神经网络迭代计算等。算法根据订单准入评价指标体系确定神经网络训练结构和GSA-GA算法的编码方式,通过训练子数据集进行神经网络训练阶段。混合GSA-GA神经网络算法如图1所示。具体步骤如下。

表 2 定性指标等级分数Table 2 Qualitative indicator grade score table

图 1 混合GSA-GA神经网络算法Figure 1 Hybrid GSA-GA neural network algorithm

式(1)中,Xi为经归一化后的样本数据,Xi∈[−1,1];X为未经归一化后的样本数据;Xmax为样本数据中一个指标的最大值;Xmin为最小值。
Step2初始化神经网络结构。神经网络结构主要为输入层、隐藏层和输出层以及各层之间的传递函数的确定。按照构建的订单准入评价指标体系,神经网络输入层节点数为12个。隐藏层节点数对训练过程有很大的影响,一般根据经验式(2)计算。根据本文研究Ni=12,No=1,确定隐藏层节点数的取值范围为[4,13],通过参数实验确定隐藏层节点数为14。选取订单准入评价值作为神经网络的输出结果,输出层节点数为1。神经网络的激活函数可以增强神经网络的表达且让网络具备更强的非线性拟合能力。本文选取tansig函数作为激活函数。式(2)中,Nq为隐藏层节点数,Ni为输入层节点数,No为输出层节点数,a为常数,a∈[1,10]。按照已确定的参数与结构可得到神经网络结构如图2所示。
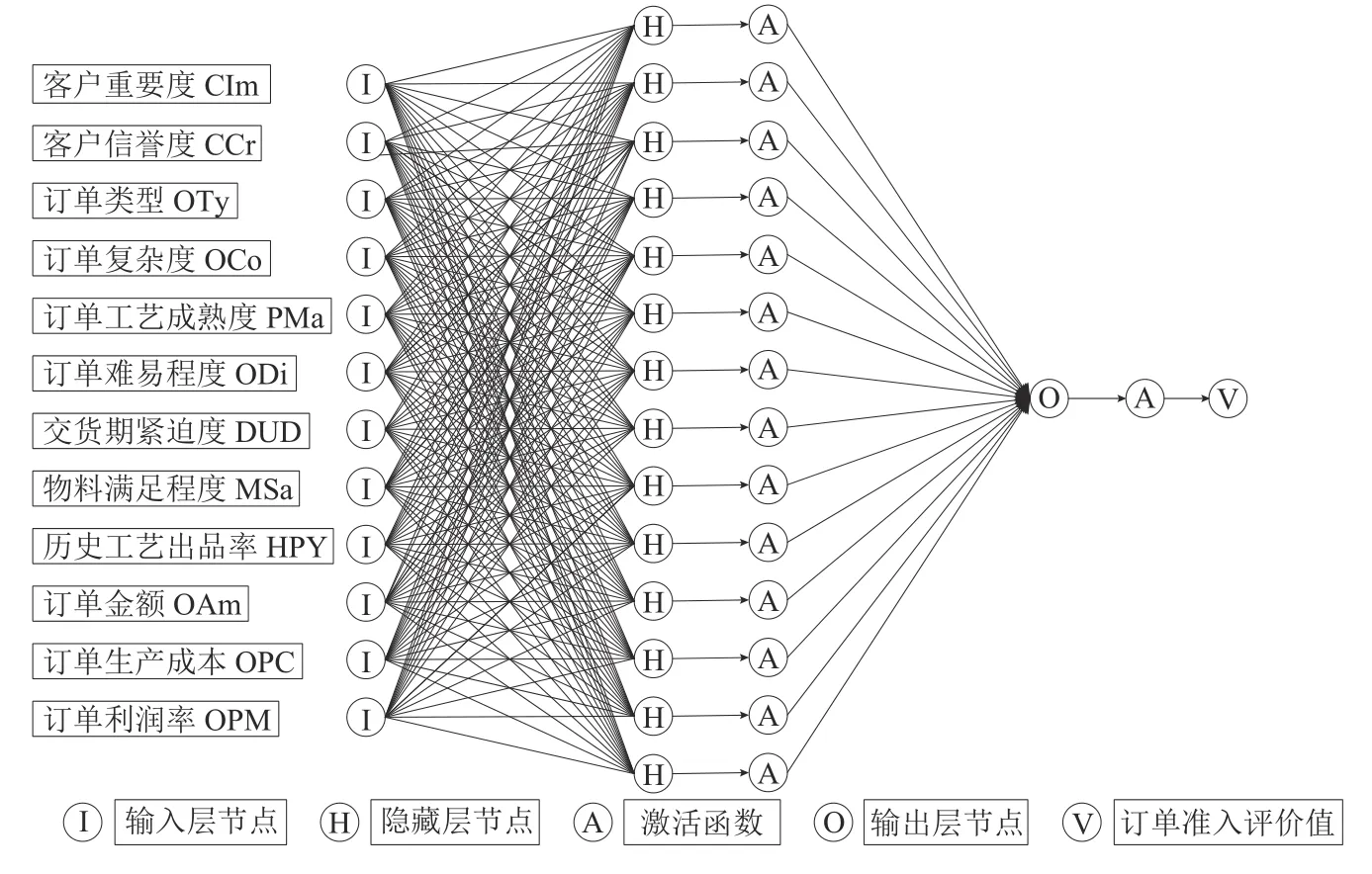
图 2 砂型铸造企业订单准入评价网络构造Figure 2 Sand casting enterprise order acceptance evaluation network construction

Step3GSA-GA算法编码结构和参数确定。通过GSA-GA算法搜索神经网络各层之间权值阈值最优组合,算法的编码结构由神经网络的输入层节点数、隐藏层节点数和输出层节点数确定。各层节点数分别为h、k、l,由此可知输入层到隐藏层的权值Vhk个数为hk,隐藏层阈值θq个数为k,隐藏层到输出层的权值Wkl个数为kl,输出层阈值θo个数为l。GSA-GA算法编码长度为N=hk+kl+k+l,编码如图3所示。算法迭代过程中,不同的参数值会产生不同的优化结果,需要根据实际问题特点来确定。本文将通过参数实验进行确定。
Step4GSA-GA算法初始化。针对所选GSA算法容易陷入局部最优和神经网络收敛速度慢的缺陷,本文采用基于Tent混沌映射的算法初始化方式。利用Tent混沌映射随机产生分布均匀的初始值可以提升粒子个体多样性以此提高算法的收敛速度,见式(3),伯努利移位变换后为式(4)。

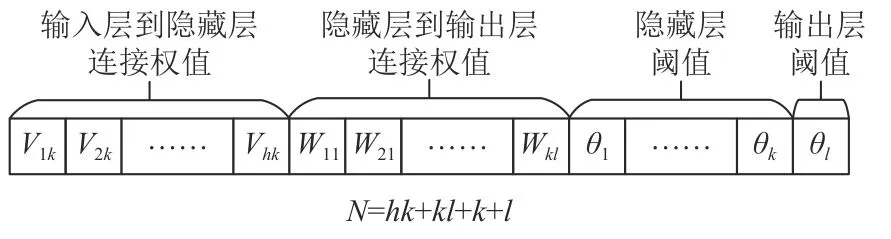
图 3 GSA-GA算法编码结构示意图Figure 3 Schematic diagram of encoding structure of GSA-GA algorithm
使用Tent混沌映射进行算法初始化伪代码如下。
Input:根据Step3已确定的编码结构长度N和初始种群大小P
其次,在实际进行教学内容分层的过程当中,必须要综合考虑学生的实际接受能力,并在此基础上保证教学内容的针对性,是每一名学生能够有效地了解到所讲解的具体内容。

通过将Tent混沌映射伪代码运行2次即可完成GSA-GA算法对粒子位置和速度的初始化。GSA-GA算法初始种群由粒子的初始位置集合和初始速度集组成。
Step5GSA-GA算法迭代运算
GSA-GA算法中的粒子代表算法在搜索空间中的候选解,在算法迭代过程中,粒子自身的属性会根据粒子之间的引力作用发生改变,且引力常数也会发生改变。在现有的智能优化算法中,虽然粒子群优化算法和引力搜索算法的原理有着本质的区别,但是这2种算法都采用了基于速度和位置的计算模型。粒子群算法的改进方法中,学者将惯性权重因子或者收缩因子引入到速度更新公式,这些因子皆改善了算法的优化性能。为改善GSA算法局部搜索能力较弱的问题和提升算法优化性能,本文在粒子位置更新公式增加系数 γ。研究表明,位置更新公式加入系数后,显著提高了基本GSA算法的优化性能[15]。粒子位置更新式为
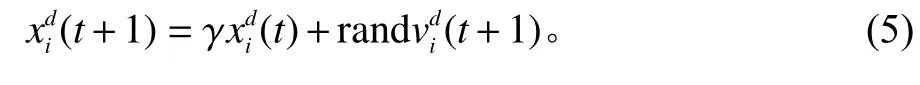
为避免算法在迭代后期收敛速度变慢,提出引力常数G动态调整策略,因此引力常数G的更新公式变为式(6),其中,权值w1=1.5,w2=1;T为最大迭代次数;t为当前迭代次数;α为衰减速率的量[16]。

全局优化过程中引入基于遗传算法的交叉算子和变异算子。根据编码结构的组成部分采取不同的交叉操作和变异操作。进行交叉变异操作之前需要进行选择操作,本文采用锦标赛方法进行选择操作。编码中权值段采取两点交叉和逆序变异操作,阈值段采取均匀交叉与互换变异操作,如图4所示。

图 4 GSA-GA算法交叉变异示意图Figure 4 GSA-GA algorithm cross-variation diagram
Step6神经网络迭代。本文选用mse(均方误差,mean squared error)作为目标函数,见式(7)。

其中,si为第i个训练样本的实际网络输出值;ri为第i个训练样本的期望输出值;O为样本个数。
网络迭代过程本文使用Adam算法取代随机梯度下降算法(SGD)来进行误差反向传播,相比于SGD算法,Adam可以避免陷入局部最优值且能提升算法收敛速度[17]。Adam计算式为
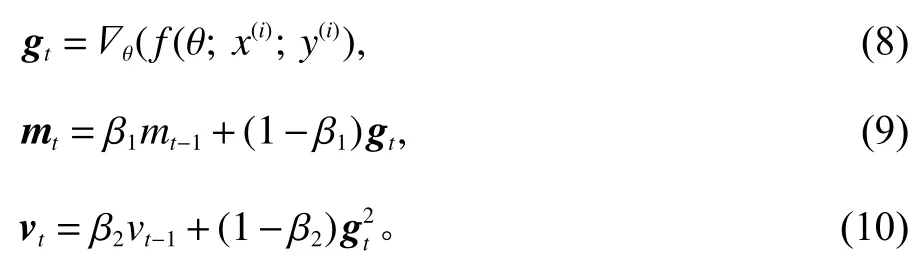
其中,gt为目标函数的梯度;x(i)为训练数据,y(i)为期望输出;mt为梯度带权平均,m0=0;vt为梯度带权有偏方差,v0=0。由mt和vt初始化是0向量,因此需要对其进行偏差修正,偏差修正公式见式(11)和(12),其中,m′为校正后的梯度带权平均;v′为校正后的梯度带权有偏方差;数值稳定的小常数β1=0.9,β2=0.999,ε=10−8,步长η为0.001。

Step7订单准入评价。GSA-GA对神经网络训练完成后可进行订单准入评价。将订单基础数据转化成指标体系中的各个指标,组成数据集,将数据集作为输入层输入到已训练完成的神经网络模型中,输出层的输出结果即为每个订单的准入评价值,通过将评价值排序,得到企业可以接受生产的订单集,并按照订单集中各个订单的评价值得到订单集中的订单优先级,以此按照生产计划的制定。
2.2 实例分析
2.2.1 数据预处理
杭州某砂型铸造企业实际生产中有大量的订单来源,且每个订单的客户信息、工艺难度、类型、交货期紧迫程度等属性均不一致。在考虑企业实际生产能力和保证盈利的前提下,迫切需要一个解决方案来对众多订单进行准入评价,以此帮助企业进行订单接收决策。本文建立基于混合GSA-GA神经网络的砂型铸造企业订单准入评价模型,采用小样本数据进行学习,选择该企业一个季度实际生产的订单数据中的25组数据,作为样本数据集训练算法,表3中数据由表1设定的订单准入评价指标体系计算所得。R1~R20为样本数据集,R1~R15为训练数据集,R16~R20为测试数据集,R21-R25为待评价订单数据集。
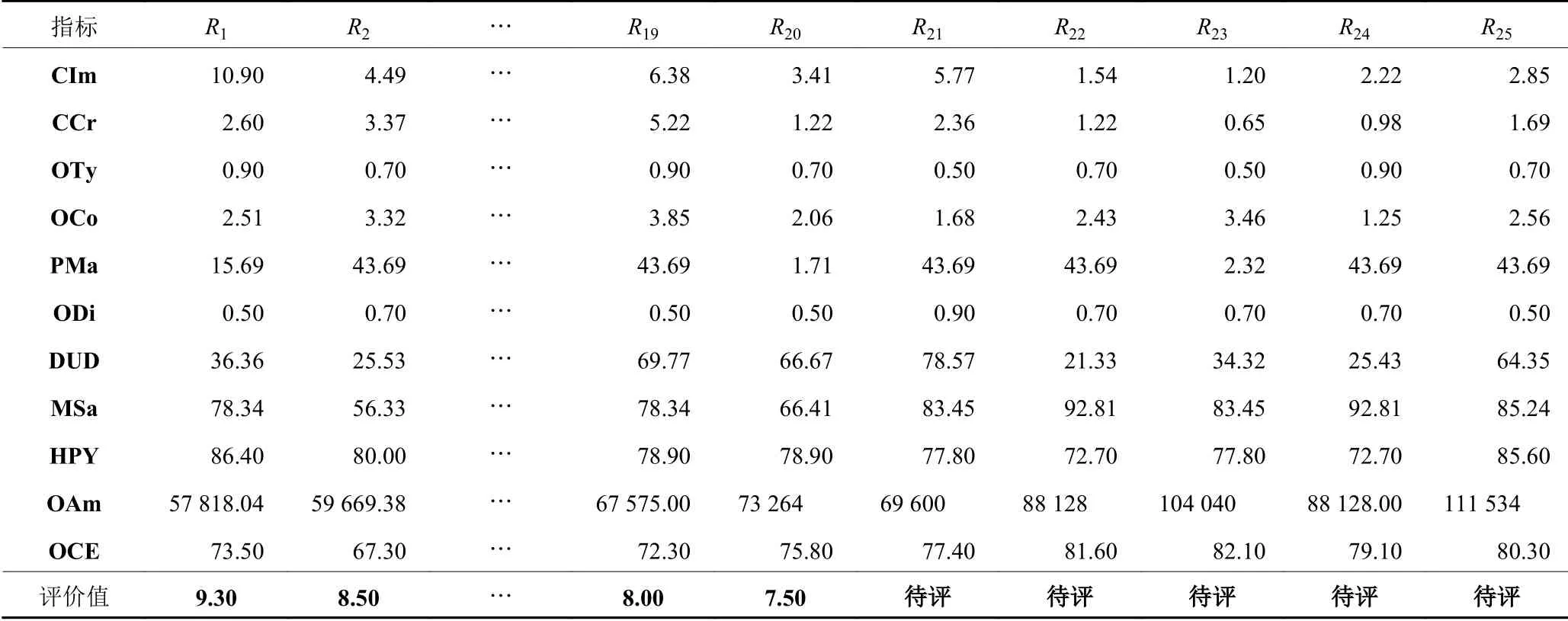
表 3 砂型铸造企业订单准入评价样本数据Table 3 Sand casting enterprise order acceptance evaluation sample data
2.2.2 参数设计
在本文隐藏层节点数是一个重要参数,若隐藏层节点数过少会导致模型的复杂度不够,无法进行充分有效的训练,即使能够进行训练也会导致误差较大和精度不高,不能达到评价的目的。若隐藏层节点数过多,虽然会使算法误差减小,但也会增加算法训练时间且消耗巨大的运算资源,降低神经网络模型的泛化能力。需要找到合适的隐藏层节点数,目前只能通过经验公式(2)和实际训练不断实验求得。本文所提GSA-GA算法中相关参数也会影响算法的效果,如种群的大小、总迭代次数等。对此,本文通过田口法实验来确定算法参数,选取隐藏层节点数(Num_HLN)、种群大小(Size_Pop)、总迭代次数(Gen_GSA-GA)为控制因子。田口法实验中控制因子的数目是3,因子水平的数目是4。控制因子数量和水平的组合见表4,选择正交阵列L16。为保证实验结构的可靠性,GSA-GA对于每组参数独立运行30次。均方误差平均响应值(MSE_ARV)是GSA-GA算法在30次获得的目标函数值(见式(7))的平均值,MSE_ARV值越小则对应的控制因子和水平组合越好。根据正交表(见表5),在图5中示出了每个控制因子水平的趋势,然后计算每个控制因子的误差平均响应值以分析每个控制因子的重要等级,结果列于表6中。
若GSA-GA算法的种群大小越大则会导致算法收敛速度越慢;若种群大小越小则会使得算法越容易陷入局部最优解。算法的总迭代次数过大会消耗很大的计算资源且会增加运行时间,过小会使得算法的训练不够充分,无法进行客观的评价。通过图5和表6可以得知,本文所建立的网络模型隐藏层节点数为14时其误差最小,也就是说隐藏层节点为14时的训练效果最好。GSA-GA算法种群大小为30,总迭代次数为30时,误差最小,会使得训练效果更好,可以更好地进行订单准入评价。
2.2.3 结果分析
通过参数实验可获得如下算法结构。神经网络输入层节点数为12,隐藏层节点数为14,输出层节点数为1,隐藏层节点阈值为14,输出层节点阈值为1,算法编码结构长度为197,种群大小为30,总迭代次数为30。基于算法参数的确定和建立的订单准入评价体系,本文使用Python基于Keras将GSAGA神经网络算法和GSA神经网络算法以及经典的GA神经网络进行对比,主要从3种算法对神经网络训练数据集和测试数据集拟合度进行分析比较。为避免算法的参数不一致导致分析比较结果不具有客观性,GSA-GA神经网络算法和GA神经网络算法参数与上述参数实验一致,GA神经网络算法参数与文献[18]一致,编码结构与本文一致。表7对15个训练数据集订单和5个测试数据集订单的实际值和评价值进行统计分析,分别计算每个订单实际值与评价值的误差以及训练数据集订单和测试数据集订单的平均相对误差。通过表7可以得知,GSA-GA、GSA、GA神经网络算法对训练数据集订单准入评价的平均相对误差分别为1.945%、8.512%、8.207%,对测试数据集订单准入评价的平均相对误差分别为为2.117%、8.419%、8.158%。GSA-GA、GSA、GA神经网络算法的训练数据集、测试数据集订单评价拟合度分别如图6~图11所示。
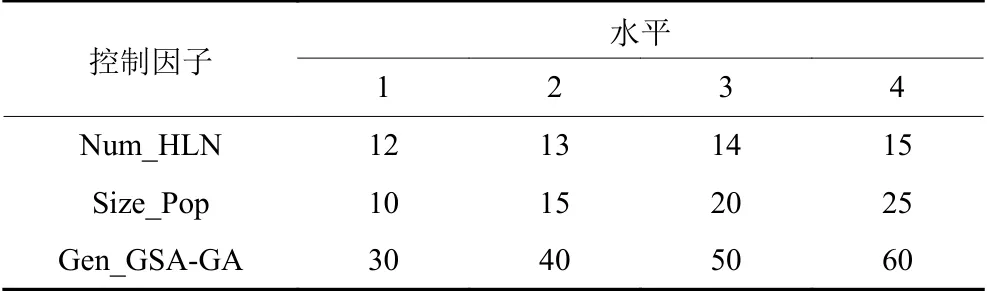
表 4 控制因子和水平组合Table 4 Control factor and level combination
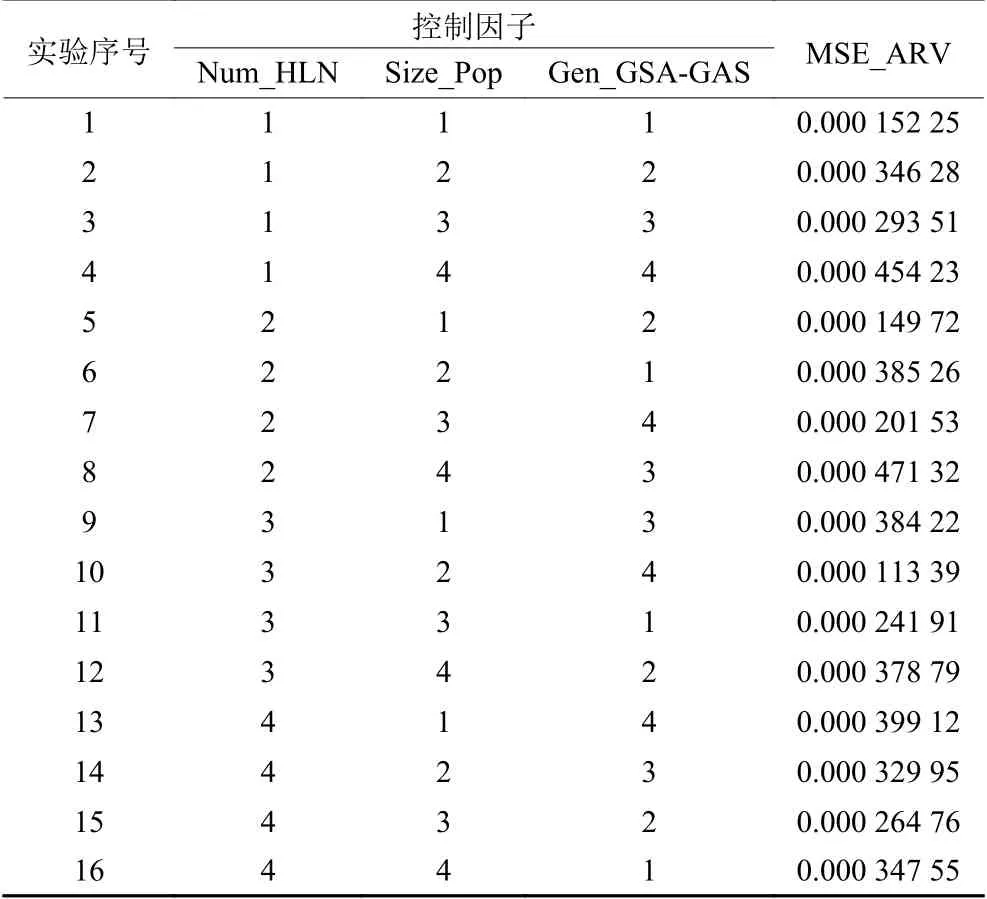
表 5 正交表构造和MSE_ARV值Table 5 Orthogonal table construction and MSE_ARV values

图 5 控制因子水平趋势Figure 5 Control factor level trend
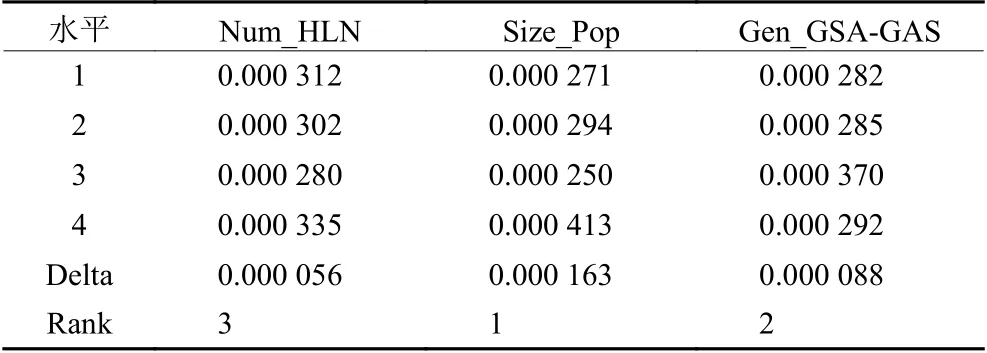
表 6 均方误差平均响应值Table 6 Mean square error average response value
综上所述,本文所提GSA-GA神经网络算法对每个训练数据集订单和测试数据集订单评价的误差均小于 GA神经网络算法和GSA神经网络算法,所提算法对砂型铸造企业订单准入评价具有很高的准确性。由图6~图11表明,本文选用的20组数据小样本数据进行学习,取得较好的拟合效果,说明选取的数据的关联特性较好。GSA-GA神经网络算法比GA神经网络算法和GSA神经网络算法对训练数据集订单和测试数据集订单的拟合程度较高。所提算法结合了引力搜索算法和遗传算法的优点,让算法能够全局最优收敛,提升了神经网络模型的评价性能和所提算法的开发能力,且有效地提高了神经网络模型训练的精度和对样本数据集订单评价拟合度。这表明本文所提GSA-GA神经网络算法在解决砂型铸造企业订单准入评价问题的优越性和很好的可行性。
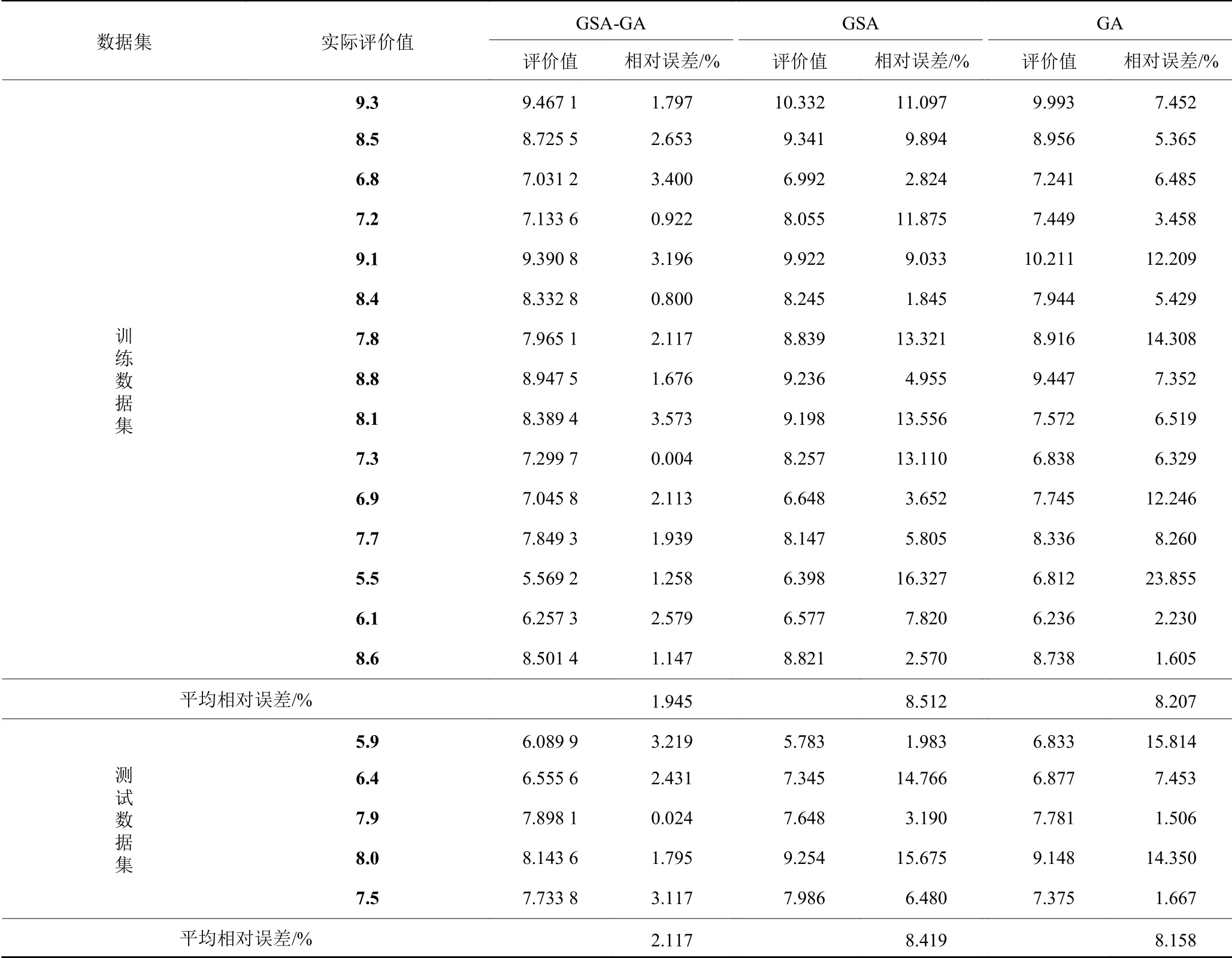
表 7 订单准入评价值统计分析Table 7 Statistical Analysis of order acceptance evaluation
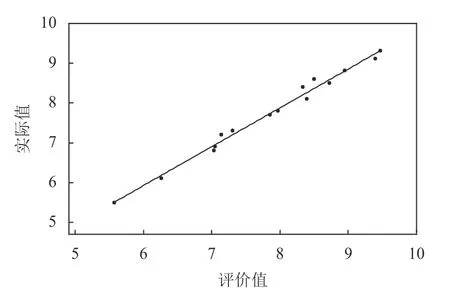
图 6 GSA-GA神经网络训练集拟合度Figure 6 GSA-GA neural network training set R-squared

图 7 GSA神经网络训练集拟合度Figure 7 GSA neural network training set R-squared
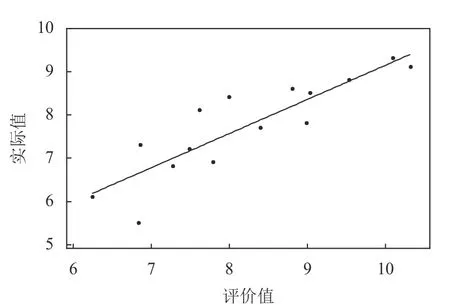
图 8 GA神经网络训练集拟合度Figure 8 GA neural network training set R-squared

图 9 GSA-GA神经网络测试集拟合度Figure 9 GSA-GA neural network test set R-squared
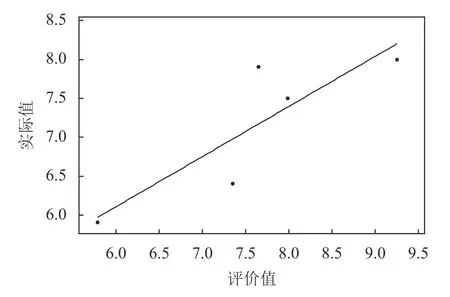
图 10 GSA神经网络测试集拟合度Figure 10 GSA neural network test set R-squared

图 11 GA神经网络测试集拟合度Figure 11 GA neural network test set R-squared
将5组待评价订单的样本数据输入使用GSAGA算法优化完成的神经网络模型中,进行订单准入评价,最终5个订单注入评价值如表8所示。通过表中数据可知,订单准入评价值得分最高的是订单R21,最低的是订单R22。订单R21、R23、R24、R25被企业接收进行生产,订单R22由于评价值过低被企业拒绝,评价结果得到该企业各个部门的认可。

表 8 待评价订单准入评价值Table 8 Acceptance evaluation value of the order to be evaluated
3 结束语
针对砂型铸造企业订单准入评价决策问题,本文设计了订单准入评价指标体系,并构建基于混合GSA-GA神经网络的砂型铸造企业订单准入评价模型。对GSA算法的种群初始化、位置更新方式进行改进,引用了基于遗传算法交叉变异算子,在神经网络模型中采用Adam算法进行误差反向传播。最后运用企业实际数据进行实例分析。结果表明本文建立模型的适用性和所提算法的有效性。本文的实验室采用小样本数据进行学习,取得较好的拟合效果,说明数据的关联特性比较好。该企业还有大量的数据,后续的研究可以提高数据容量,继续验证算法的有效性。订单只是企业生产中开始的环节,并没有与整个砂型铸造企业生产车间调度问题相结合。这将是下一步研究的内容。

