装配作业车间分批调度问题的算法对比

曾垂飞，刘建军，陈庆新，毛 宁

(广东省计算机集成制造重点实验室 广东工业大学，广东 广州 510006)

在生产及组合优化领域，车间调度一直属于研究中的热点问题[1]。装配作业车间调度问题(assembly job-shop scheduling problem，AJSP)蕴含着复杂的生产制约关系和动态因素，既要考虑零件的加工工序次序约束，又要考虑装配零件之间加工进程的协调，往往具有更高的复杂度[2]。

目前关于AJSP的解决方法主要分为2类：基于优先级分派规则调度和启发式调度算法[3-4]。然而，这些研究绝大多数都基于一个前提，即车间调度的任务都不考虑拆分。在实际生产过程中，分批优化调度问题[5-6]的加工任务往往具有一定批量，如果考虑任务拆分，允许分批生产，那么后续工序就可以提前开工，并且降低其生产完工周期。目前国内外已有许多针对分批优化调度问题的研究，按照车间及加工特性的不同可分为柔性作业车间[7]、作业车间[8]、流水车间[9]。此外，根据分批优化调度方法的不同可分为启发式算法[10]、元启发式算法[11]、群体智能算法[12]。分步优化和集成优化是处理问题的2种常见策略[13-14]。分步优化是计划阶段进行批量划分，调度阶段进行子批排序；集成优化是将批量划分后的分批方案进行排序，得到整体方案适应函数值，而后进行迭代优化，因此，集成优化是将批量划分和子批排序2个子问题加以联合处理。文献[15]中染色体编码方式采用两级编码，针对柔性作业车间分批优化调度问题提出多目标差分算法。文献[16]以生产周期为优化目标，针对装配作业车间分批优化问题提出混合粒子群优化算法和混合遗传算法，并对算法性能做了比较分析。文献[17-18]将分批与调度两个子问题分别利用遗传算法与调度规则进行分层迭代求解。

基于以上分析，目前考虑装配作业车间分批调度优化的研究仍比较少见。本文综合考虑上述调度问题的特性，基于两个子问题处理方式的不同，分别提出改进型集成优化算法、混合求解算法和双层遗传进化算法。最后通过仿真实验对所提算法的求解效果、收敛速度、运算时间以及适用范围进行对比和分析。

1 问题描述

问题描述如下：车间具有p个产品，总计N个批量生产任务、M台机器，根据需要将批量任务进行拆分，将拆分后的子批分配到对应加工资源，且在各产品下属子批零件全局齐套后进行装配(假定一个装配工期，并不考虑装配资源约束)。在满足人机料法等资源约束条件的同时优化对应的生产指标。本文优化目标为最大完工时间，根据优化目标，最终生成具有可执行性并能够指导实际生产且实现生产指标最优的调度方案。

约束条件：1) 每台生产设备仅代表一道工序，但其零件的生产加工时间不同；2) 不考虑人员技能、班组出勤、设备故障、模具/物料短缺等扰动因素；3) 子批内零件定义为一个加工生产批次，即同一加工单元同一时刻只能连续不断地加工同一子批，待其生产完后统一进行搬运，不考虑生产中断，不考虑设备故障，不考虑批次内零件搬运时间等且子批内零件共享该生产批次的setup时间。

2 模型建立

2.1 参数定义

为了简单而准确地描述问题，本文详细定义了涉及的相关参数，具体含义如表1所示。

表 1 参数定义Table 1 Definition of parameters

2.2 数学模型

本文构建以最大完工时间最小化为优化目标的数学模型。

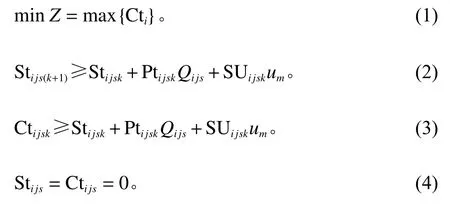
式(1)定义了优化目标的约束形式；式(2)对加工任务的工艺路线进行相关约束；式(3)对加工任务的排队等待时间进行相关定义；式(4)表示在初始时刻所有加工任务的上机概率均等；式(5)对产品的最大完工时间进行定义；式(6)和式(7)定义分批数量Nui j与分批大小Qijs；式(8)定义当前加工单元上的连续加工任务类型是否可共享setup时间。

3 算法设计

3.1 混合求解算法设计

关于AJSP的分批调度问题研究，在实际生产车间环境中，由于其关注点和资源约束的差异化，从而存在着多种形式的优化指标。混合求解算法从计算效率及决策及时性的角度出发，基于分层迭代优化策略，设计了遗传算法和排序规则递阶嵌套的算法结构。批量任务的分批方案由外层GA确定，基于优先级分派规则的内层子批排序则以外层的批量划分结果为调度对象。

3.1.1 混合求解算法的总体流程

该算法的总体流程如图1所示，具体求解步骤如下。

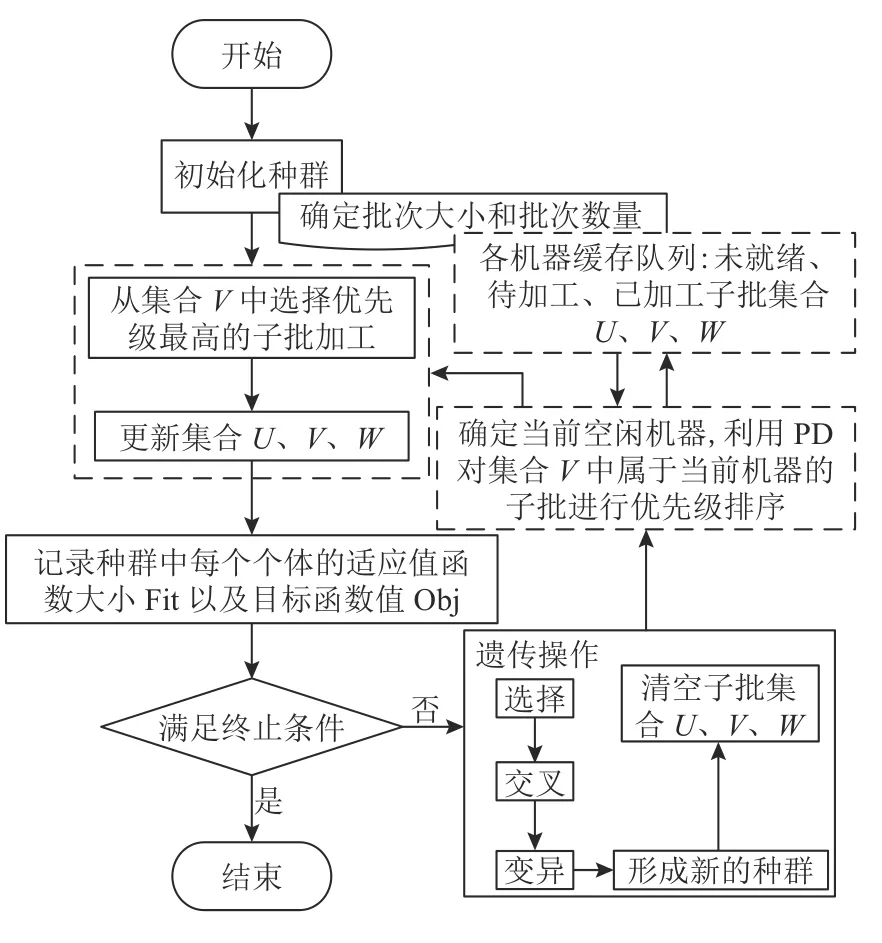
图 1 混合求解算法流程Figure 1 The process of hybrid algorithm

1) 初始化参数，如遗传参数、模型参数等。

2) 初始化种群，通过不同的编码方式构造染色体。

3) 将待加工子批预排产到对应加工中心或生产机器；将所有子批划分为3个集合U、V、W。集合U：加工子批存在前工序约束，当前时刻不具备上机条件；集合V：当前时刻满足上机条件，允许加工；集合W：已完成上机加工操作。

4) 通过规则选择各机器任务池内优先级最高任务进行加工，执行结束后更新任务集合。

5) 判定是否满足终止条件。

3.1.2 优先级分派规则的选取

优先级作业分派规则的选取原则主要基于实际生产环境中的产品生产工艺特点、车间优化指标、生产资源约束以及是否能够高效率地获取较高质量的可行解。关于优化车间最大完工时间的性能指标，1971年Siegel学者研究发现TWKR (Total Work Remaining)规则针对此类指标优化效果最好。因此，当前算法利用TWKR规则解决子批排序问题，其计算公式为

3.1.3 编码与解码

基于多层实数序列的编码形式将每个批次零件随机拆分成若干个不同大小的子批进行组合，具体编码如图2所示。

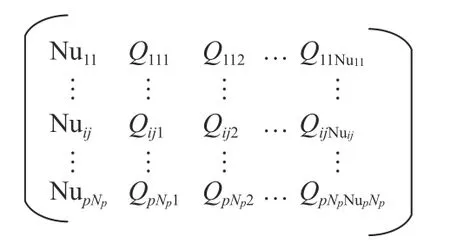
图 2 染色体编码方式Figure 2 The mode of chromosome

在实际生产过程中，批量零件的分批方式多种多样，本文主要考虑可变分批和等量分批。可变分批是首先随机生成子批数量，其次利用随机函数随机生成若干不等大小的子批；等量分批是针对批次零件进行均等拆分，不能完全均分时，规定批次大小Qijs向下取整，且需满足

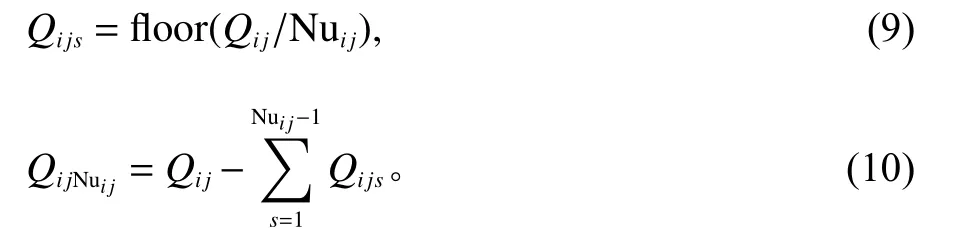
3.1.4 交叉操作

假定在当前计划时期，有一订单P，N1=3，Q11=4,Q12=5，Q13=7，Nu11=2，Nu12=3，Nu13=3以及Nu21=2，Nu22=2、Nu23=2，交叉位置r=2。具体如图3所示。

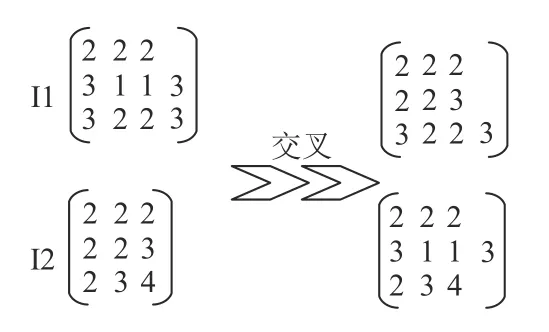
图 3 交叉操作Figure 3 Cross operation

3.1.5 变异操作

假设当前有一染色体片段其批次数量为3，批次大小分别为Nu11=2，Nu12=3，Nu13=3，此时，随机生成变异点r=3，再根据等量划分策略，生成各批次大小，具体如图4所示。

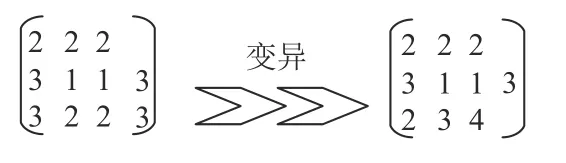
图 4 变异操作Figure 4 Mutation operation

3.1.6 选择操作

在遗传算法中，选择算子是通过模拟自然界的优胜劣汰，适者生存的过程，从种群中不断选择优胜的个体，通过选择操作把优化的个体遗传到下一代，本文采用轮盘赌选择法。

3.2 双层遗传算法的设计

3.2.1 双层遗传算法的总体流程

基于批量任务拆分和拆分后子批排序的两阶段调度任务，该算法设计了2层GA递阶嵌套的形式，即在加工任务的一次迭代过程中，外层GA产生分批方案。内层GA搜索当前分批方案的最佳排产方案。具体流程如图5所示。

3.2.2 编码与解码

该算法基于批量拆分和子批调度设计了双层递阶嵌套的形式，因而其染色体也分为2层。外层染色体编码及其结构在前文3.1.3小节中已详细说明，此处不予赘述。内层染色体编码采用x-y形式(即零件x的第y批次)表示各子批工序的生产加工顺序，x-y出现的频次表示其工序次序。具体结构如图6所示。

3.2.3 交叉操作

由染色体编码结构可知，该算法的交叉可分为批量划分和子批调度两部分。前者采用单点交叉，详细说明已在前文3.1.4小节说明，此处不予赘述。后者基于零件交叉，如图7所示，随机生成零件种类x=2，调换两父代染色体2-y所有位置的编码基因。

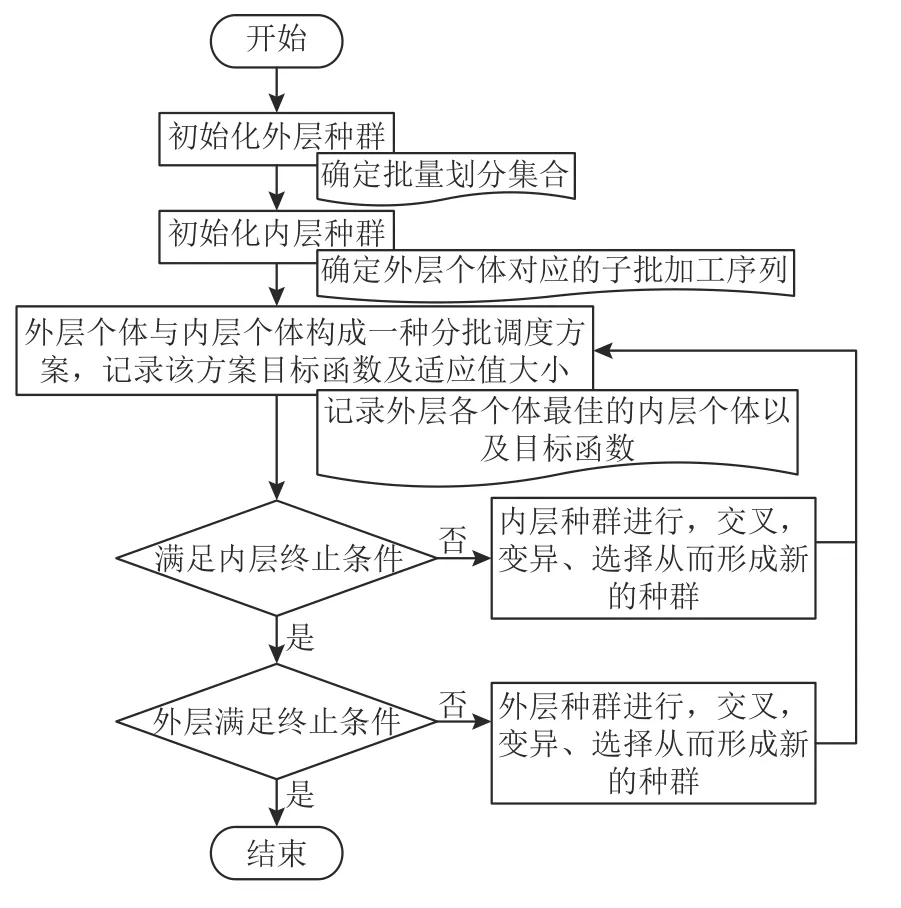
图 5 算法流程Figure 5 The process of algorithm

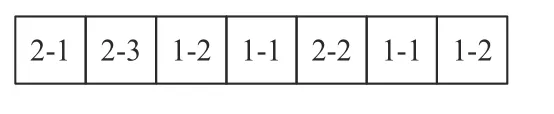
图 6 内层染色体片段(子批生产加工序列)Figure 6 The fragment of intener chromosome

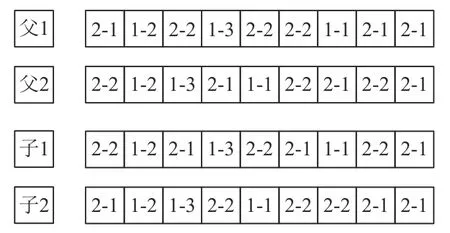
图 7 交叉操作示意图Figure 7 Diagram of cross operation

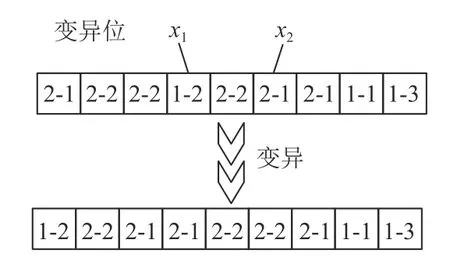
图 8 变异操作示意图Figure 8 Diagram of mutation operation

3.2.4 变异操作

该算法的变异操作同样分为批量划分和子批排序两部分。前者采取实值变异，详细说明已在前文3.1.5小节中说明，此处不予赘述。后者基于零件变异，如图8所示，首先生成随机数x1、x2，x1＜x2，且x1，x2∈[1，基因长度]，随后将x1至x2变异点之间的基因换到首位从而形成新的个体。

3.3 改进型集成优化算法的设计

3.3.1 改进型集成优化算法的总体流程

该算法流程如图9所示。

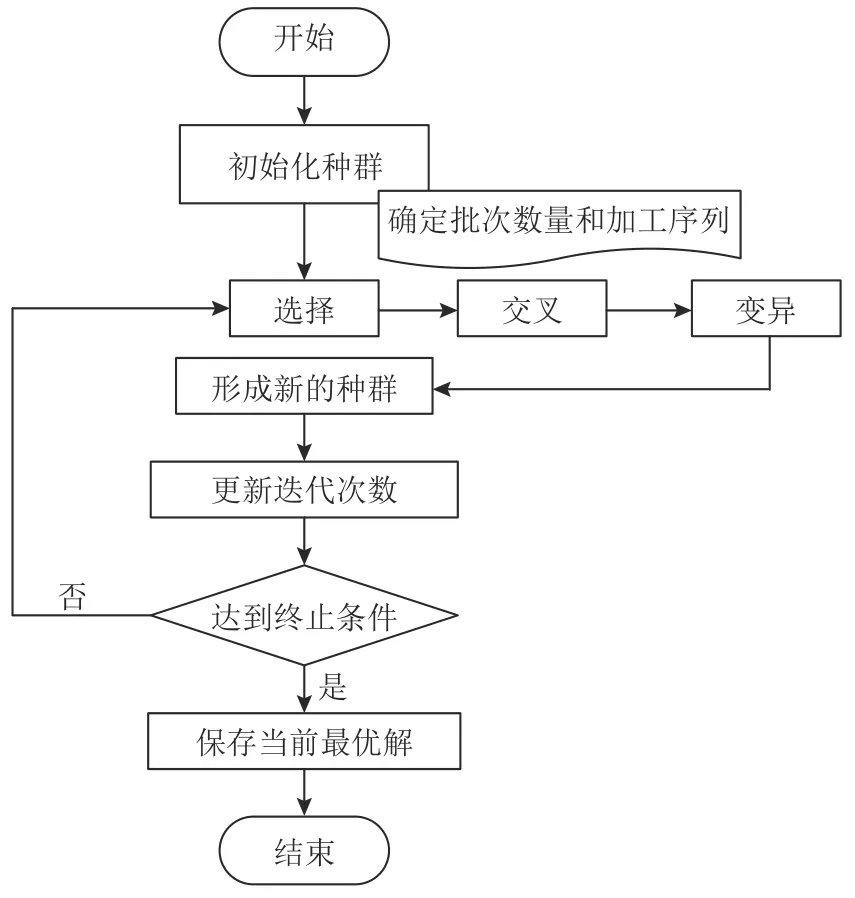
图 9 改进型集成优化算法流程Figure 9 The process of improved integrated optimization algorithm

3.3.2 编码与解码

该算法将批量划分和子批排序2个任务进行集成编码，如图10所示。

图 10 编码模型Figure 10 The model of encode

具体示意如表2所示，N1=3, Nu11=2, Nu12=2,Nu13=2,m11=1,m12=1,m13=1。

表 2 示意表Table 2 Sketchdiagram

3.3.3 交叉操作

交叉算子是该算法中最重要的算子，它决定其全局收敛性，保证子代可行性的同时使子代继承父代的优良特征，其交叉示意图如图11所示，具体步骤说明如下。

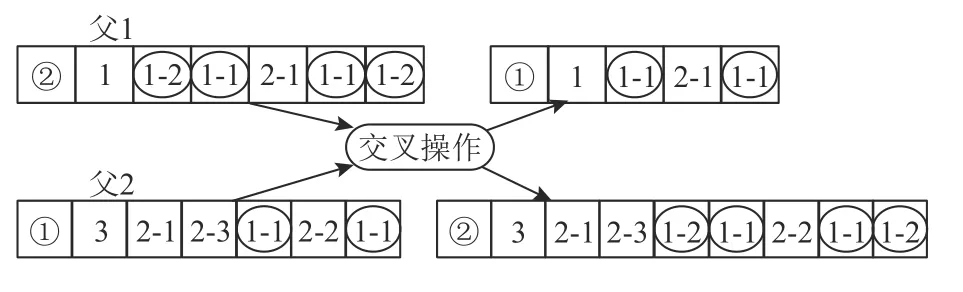
图 11 交叉操作示意图Figure 11 Diagram of cross operation

2) 根据交叉点记录“子批加工序列”段染色体对应子批总数量y1、y2，且y1＞y2；

3)k=floor(y1/y2)，当k＜2时，对应零件的基因位依次交换即可；当k≥2时，基因位按k倍依次进行交换。

3.3.4 变异操作

该算法基于染色体结构，分别设置“零件分批数量”和“子批加工序列”2种变异方式，在“零件分批数量”段针对染色体进行单点变异，变异操作示意如图12所示。

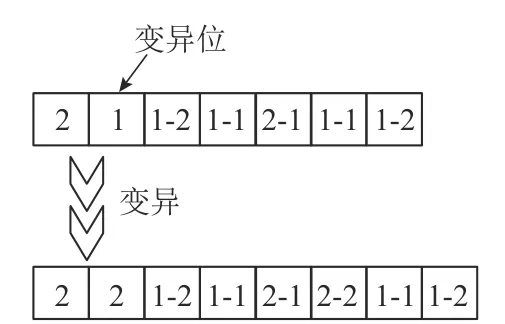
图 12 变异示意图(基于零件分批数量段)Figure 12 Diagram of mutation operation

在“子批加工序列”段针对染色体进行传统交换变异，详细说明已在前文3.2.4小节中说明，此处不予赘述，具体操作示意如图13所示。

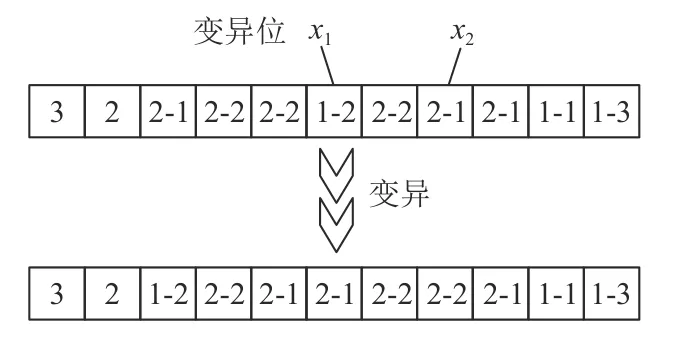
图 13 变异示意图(基于子批加工序列段)Figure 13 Diagram of mutation operation

4 仿真实验和结果分析

4.1 仿真实验设计

仿真过程中涉及到的具体实验参数如表3所示。

实验程序以最小化最大完工时间作为优化目标，实验变量4×3×3=36，每组变量重复做10次，取最优解，故共有(4×3×3)×10=360组实验，模型参数m=5,Q∈[4,10],k∈[1,m], Pt ∈[5,10]，经参数对比性实验分析后，遗传参数PS=100, MAXGEN=200, Pm=0.01, Pc=0.7, GGAP=0.8，该实验设计主要由3部分组成，具体设计如表4所示。

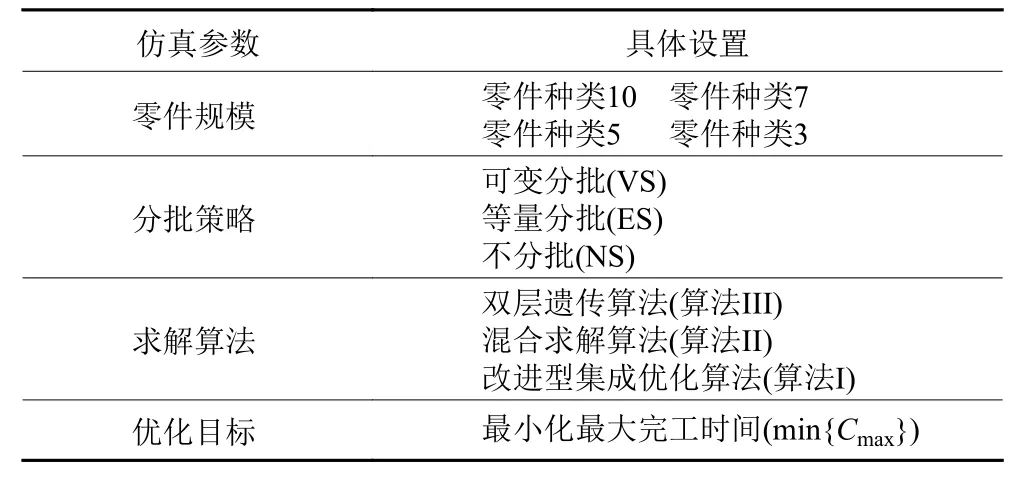
表 3 仿真实验参数设置Table 3 Parameter setting of simulation experiment

表 4 仿真实验设计Table 4 The design of simulation experiment

4.2 实验结果与分析

图14从零件规模、分批策略的维度，展示算法I、II、III在最大化完工时间上的优化程度。图15展示在可变分批策略下基于不同零件规模，其算法I、II、III收敛性能的比较分析。详细数据如表5、表6所示。

综上所述，1) 在相同的零件规模下，不考虑收敛性以及计算时间，对目标函数优化效果最好的是双层遗传算法，其次是改进型集成优化算法，但在零件规模增大至10时，其优化效果急剧下降；2) 在相同的零件规模并且其迭代优化充分的情况下，可变分批对目标函数优化效果最佳，其次是等量分批；3) 在多种求解算法中，算法II的收敛性最快；算法III和算法I收敛依次降低，但是随着零件规模的增大，算法I收敛性愈是弱于算法III。

5 结束语

本文根据装配作业车间加工任务的批量划分和子批排序的两阶段调度任务的不同处理方式，提出了以最小化最大完工时间为优化目标的3种不同求解算法。各算法分别从从零件规模、分批策略等多种维度验证了其有效性。实验数据表明：1) 在不考虑计算效率和算法收敛速度的情况下，VS性能优于NS，否则，反之；2) 车间产品类型超过一定规模，即零件规模大于10后，现有的仿真实验环境已不足以得到高质量的解(解空间爆发性增长，搜索范围急剧扩大)；3) 产品生产过程中，由于管理侧重点、目标函数以及约束形式不一，算法II总是可以较高效率地获取高质量的可行解；4) 如果车间产品较为单一，采用算法I可快速得到高质量的全局优化解；5) 算法III相比于集成算法，其内层的迭代搜索降低了重复搜索的概率，在不考虑运行效率以及车间多种目标函数和约束的情况下，算法III在上述问题情况下都可得到较高质量的解。鉴于本文只考虑了车间订单的全局齐套性，因此，对于未来的研究工作，笔者认为可以结合现状引入其他约束，如装配层级复杂度、准备时间设置比例、有限的缓存区大小、机器资源(预防性维护、保养)等。

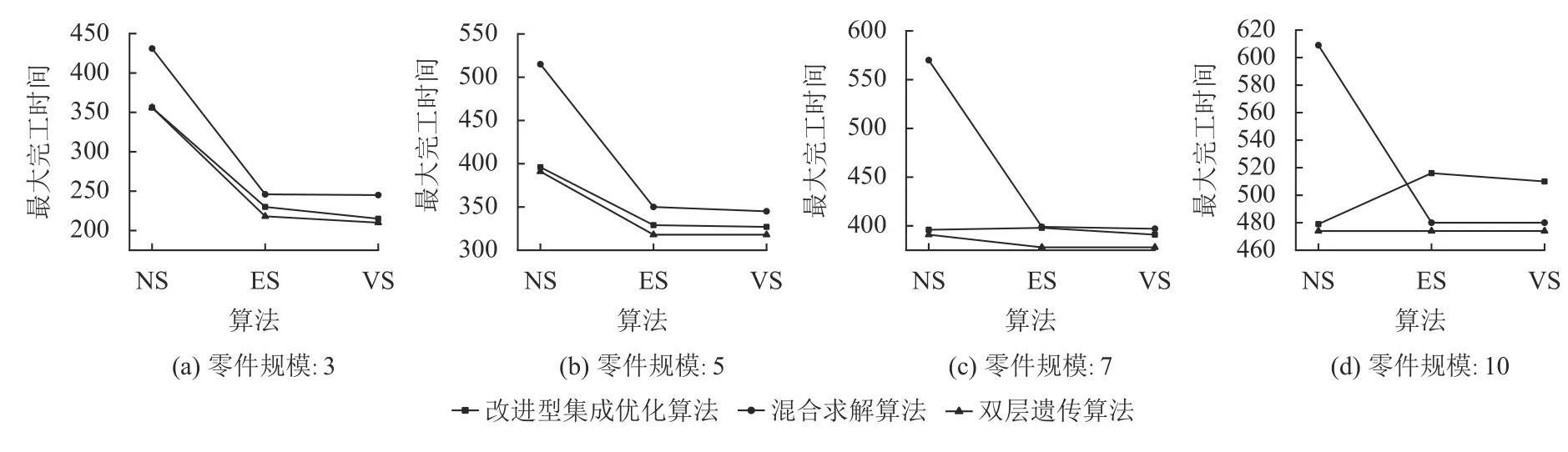
图 14 完工时间优化比较Figure 14 Comparison of completion time optimization

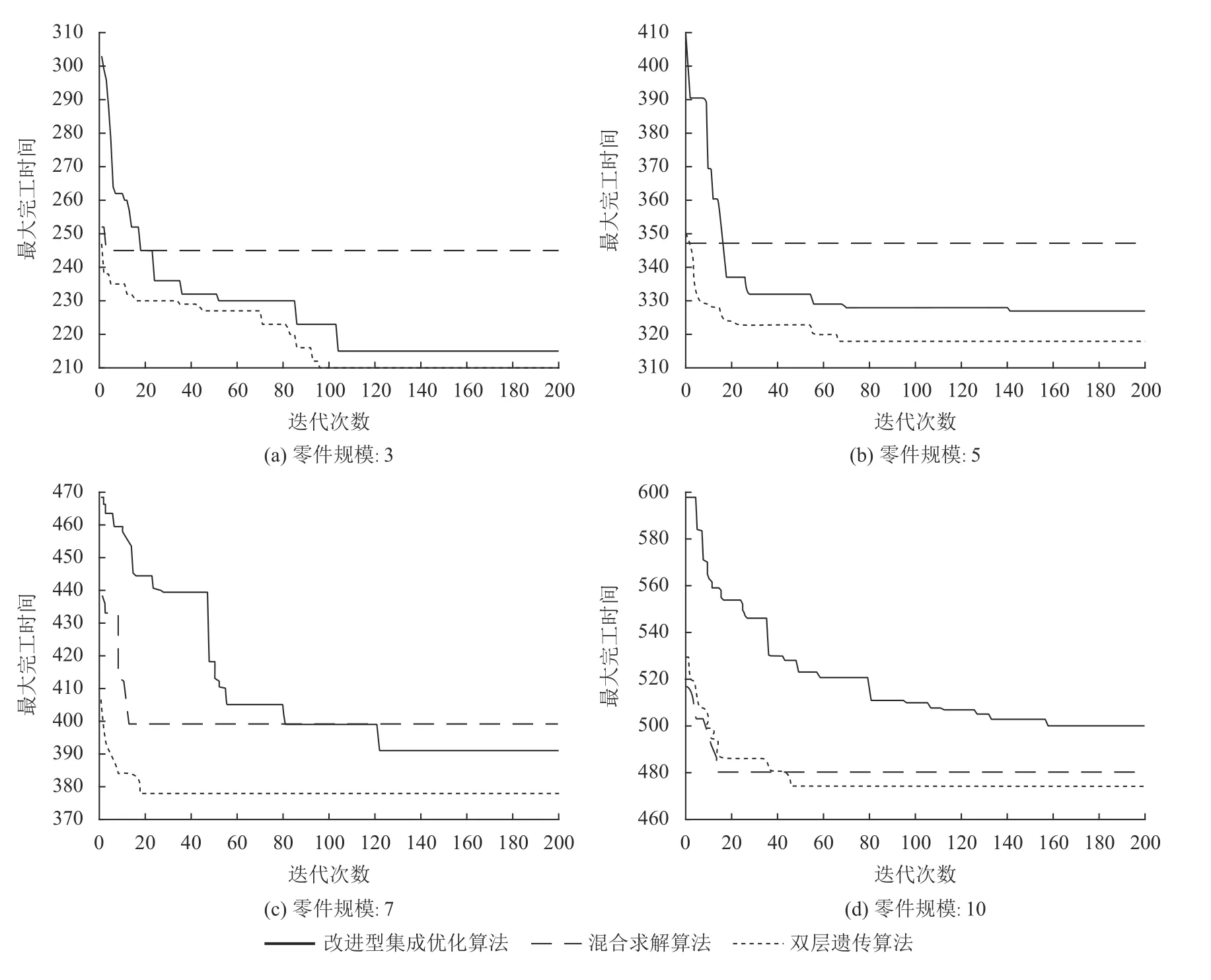
图 15 收敛速度比较Figure 15 Comparison of convergence rateperformance

表 5 实验对比详细数据(一)Table 5 Detailed data of experimental comparison (一)

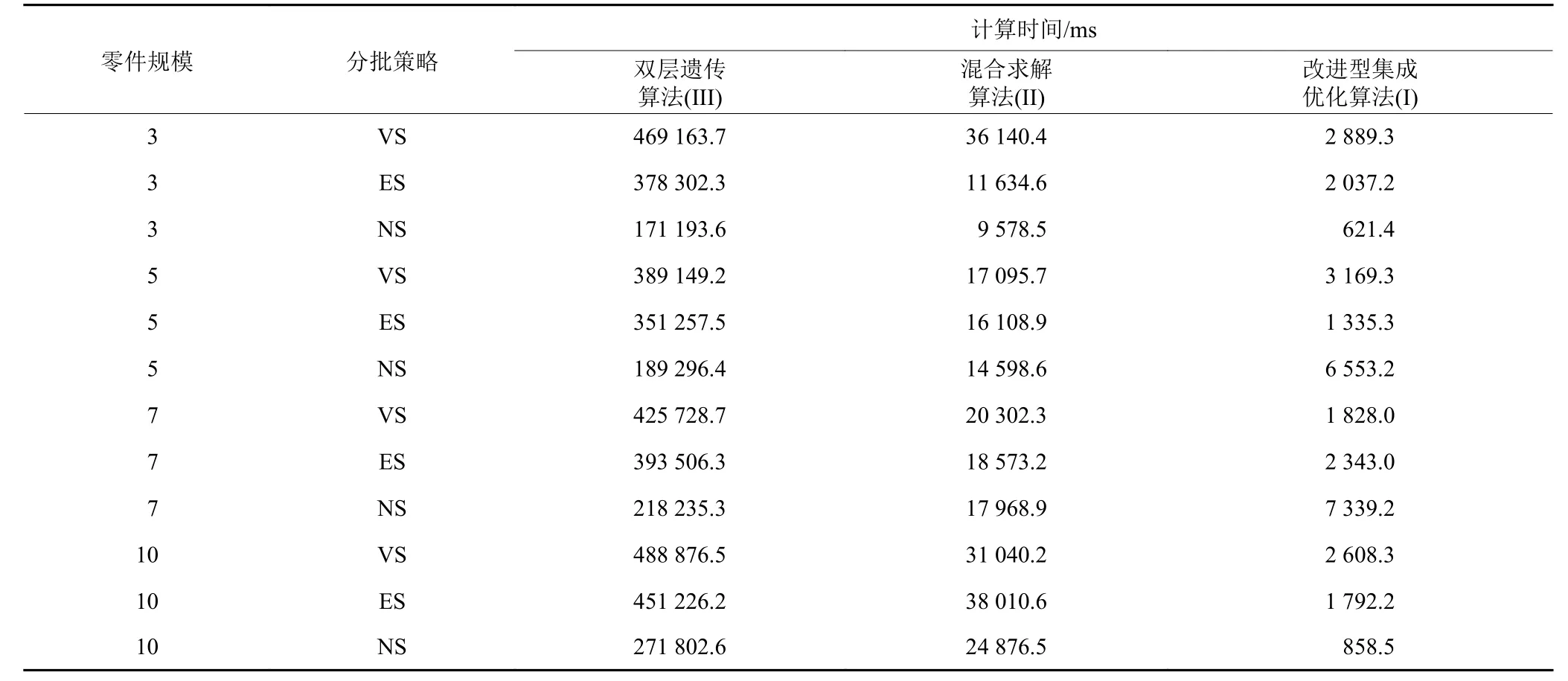
表 6 实验对比详细数据(二)Table 6 Detailed data of experimental comparison (二)