原油一次加工过程的多目标调度优化
侯 艳,黄康焕,张亿仙,伍乃骐
(广东工业大学 1.计算机学院;2.机电工程学院,广东 广州 510006)
原油一次加工过程具有生产规模大、约束多、过程连续、装置多和工艺复杂等特点,是一个包含离散事件和连续过程的混合系统,其短期生产计划和调度问题属于NP-hard问题[1]。短期生产计划是炼厂根据市场需求和国际油价变化等因素制定的7~10天生产计划。目前仍然缺乏成熟的商用软件和技术用于制定原油处理过程短期生产调度计划,大部分工作需要决策者手工完成。而优化的调度计划能够显著提高炼厂的利润。因此,如何制定优化的调度计划成为研究的热点之一。
部分学者通过数学规划方法对调度问题进行求解。Wu等[2]通过线性规划方法对输油管道的输油过程进行建模,降低管道转运原油过程中消耗的能量;Hamisu等[3]通过将炼油调度周期等分为若干个时间间隔,即离散时间表示,对原油处理过程建立混合整数线性规划模型,降低油轮卸油成本、油轮在海上的等待成本、油罐库存成本和切换成本;为了保证求解的精度,离散时间表示需要将调度周期等分为尽可能小的时间片,导致产生大量的二元决策变量。现有软件不能很好地求解大规模问题,而连续时间表示能够有效减少决策变量的数量。Zhang等[4]考虑管道的长距离运输,以原油卸载成本、库存成本、原油混合成本等为优化目标,采用连续时间表示,建立混合整数非线性规划模型。陈璇[5]对沿海型和内陆型原油调度问题建立连续时间模型,降低油轮海上等待成本等操作成本。连续时间表示虽然能有效减少决策变量的数量,但是容易产生非线性约束,导致求解非常困难,在实际应用中不可行。另外,数学规划方法用于求解调度问题时,要求短期生产计划已知。然而在制定详细调度前,短期生产计划未知,因此,数学规划方法不能直接应用于原油短期生产调度。
为了解决这个问题,Wu等[6]采用Petri网对原油处理过程进行建模和分析,将生产调度问题划分为上下2个层次。上层采用线性规划得到蒸馏塔炼油计划以最大化生产速率;下层制定原油详细调度计划以实现上层的炼油计划。文献[7-8]分别采用启发式算法和混合整数规划模型对原油调度问题建模,求解优化的调度计划。文献[9-12]根据两层模型和控制理论,采用Petri网对系统的可调度性进行分析,得到各种情况下的可调度性条件。然而据此得到的详细调度计划不一定是一个最优的调度计划。
为了制定优化的详细调度计划,Hou等[13]将原油短期调度问题转换为供油罐和蒸馏塔的指派问题,以系统的可调度性条件为安全边界,通过指派蒸馏塔和供油罐执行调度决策,启发式地寻找原油的详细调度计划以实现上层的炼油计划。同时,以供油罐使用个数成本、罐底混合成本、管道混合成本以及蒸馏塔的供油罐切换成本为优化目标,通过采用NSGA-II算法[14]寻找问题的Pareto最优解。
原油处理过程短期生产调度问题是多目标组合优化问题。进化算法常用于求解多目标优化问题。陈祥等[15]采用文化基因算法求解开放车间调度问题;Jiang等[16]采用粒子群算法求解云制造供应链调度的多目标优化问题。对于高维多目标进化算法,多样性和收敛性是评价算法性能的2个重要指标。为了提高进化算法的多样性和收敛性性能,本文在文献[13]已经将原油短期调度问题转换为供油罐到蒸馏塔的指派问题的基础上,提出基于改进的骨干粒子群算法(improved bare bone particle swarm optimization, I-BBPSO)和NSGA-II算 法协 同进化 的双种群进化算法(bare bone particle swarm optimization and NSGA-II, BPGA)对原油短期调度问题进行求解。
1 问题描述和数学模型
1.1 问题描述
炼厂的运作过程有3个阶段:原油一次加工过程、生产过程和成品油转运。图1为原油一次加工过程示意图。首先,油轮将原油卸载到储油罐中;接着,输油管道将港区储油罐中的原油转运到厂区供油罐中;最后将供油罐中的原油供给蒸馏塔进行分馏。原油一次加工后得到的石油半成品经过后续的混合加工后,最终得到需要的石油产品,并将其运输到市场。

图 1 原油一次加工过程Figure 1 Crude oil operations
原油经过卸载、转运和供油3个阶段后,产生一系列的成本。
1) 油轮在港口等待卸油时,根据停泊时间长短需要向港口缴纳相应的费用;
2) 油轮向不同的港区储油罐卸载原油时,产生切换成本;
3) 输油管道转运原油时产生能耗成本;
4) 输油管道转运原油时,管道中不同种类的原油在交汇处产生混合成本;
5) 供油罐向外放完油后,不能挤出罐中的所有原油,罐底还剩余一部分原油;当该油罐进行下一次充油时,不同种类原油就会在罐底混合,混合后的原油品质下降,产生原油的混合成本;
6) 蒸馏塔在炼油期间,需要切换多个供油罐为其供油,产生切换成本;
7) 原油一次加工过程产生供油罐使用成本。
蒸馏塔炼油计划为蒸馏塔DSk具体的炼油时间、分馏的原油种类,以及相应的原油体积。本文基于炼厂已有的蒸馏塔炼油计划,假设港区储油罐有足够的原油可供调度,输油管道以最大的输油速率fpmax将原油从港区储油罐转运到厂区供油罐,制定优化多个目标的原油详细调度计划,以实现蒸馏塔的炼油计划。因此,本文目标是优化上面提到的成本(4~7)。
1.2 数学模型
1.2.1 符号说明
Λ为待处理的原油类型总量;
K为蒸馏塔的数量;
∆为供油罐个数;
OD为原油调度决策;
COT为原油类型;
S为原油输入的来源;
D为原油输出的目的地;
[a,b]为 OD的起始时刻和结束时刻;
V为 OD转运的原油体积;
Θ={1, 2,···, Λ},为待处理的原油类型集合;
DS={1, 2,···,K},为蒸馏塔集合;
TK={1,2,···, ∆},为供油罐集合;
TKr为供油罐r;
DSk为蒸馏塔k;
Φ为原油在供油罐中的驻留时间;
τs、 τe分别为蒸馏塔炼油计划的开始时刻和结束时刻;
dij为i号原油和j号原油在管道的混合成本系数;
αij为i号原油和j号原油在管道中的混合次数;
cij为i号原油和j号原油在供油罐中的罐底混合成本系数;
βij为i号原油和j号原油在供油罐中的罐底混合次数;
σ为一个供油罐的使用成本系数;
φ为原油一次加工过程使用的供油罐总个数;
ω为蒸馏塔切换一次供油罐的成本系数;
γk为DSk切换供油罐的次数;
Cr为TKr的容量;
vr(ϑ)为ϑ 时刻TKr中的原油体积;
Qr,COT(ϑ)为ϑ 时刻TKr中原油种类的数量;
Sk(ϑ)∈{0,1}, ϑ时刻,1表示DSk正在炼油,0表示DSk没有炼油;
QTKk(ϑ)为ϑ 时刻向DSk供油的供油罐数量;
Sr,in(ϑ)∈{0,1}, ϑ时刻,1表示TKr正在充油,0表示TKr没有充油;
Sr,out(ϑ)∈{0,1}, ϑ时刻,1表示TKr正在放油,0表示TKr没有放油。
1.2.2 问题数学模型
五元组OD=(COT,V,S,D,[a,b])表示原油调度决策。根据原油输入的来源地和输出的目的地,OD分为原油卸载决策ODU(S为油轮,D为港区储油罐)、原油转运决策ODT(S为港区储油罐,D为厂区供油罐)以及供油决策ODF(S为厂区供油罐,D为蒸馏塔)。原油的详细调度计划需要保证炼油计划在时间域[τs,τe]能够完成。
目标函数为

其中,f1为管道中原油的混合成本;f2为供油罐罐底原油的混合成本;f3为使用供油罐的总成本;f4为蒸馏塔切换供油罐产生的成本。
约束条件为
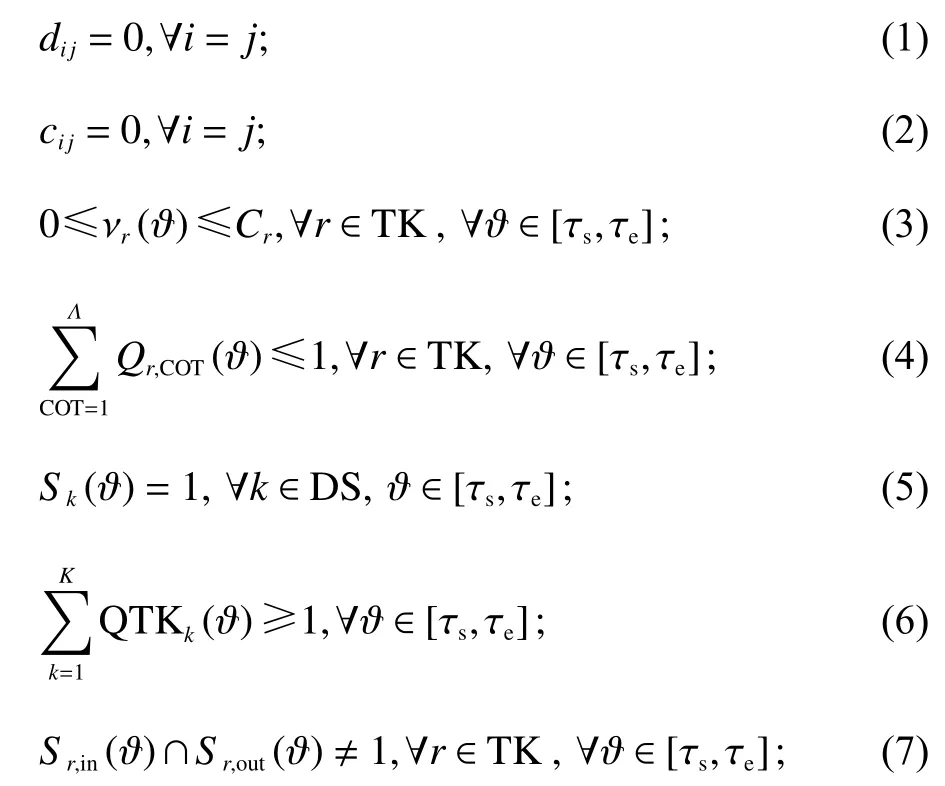
式(1)表示相邻2次ODT的原油种类相同时,管道中原油混合成本系数di j为0;式(2)表示TKr前后2次装载原油的种类相同时,原油混合成本系数cij为0;式(3)表示任意时刻 ϑ,TKr中的原油体积满足供油罐容量约束;式(4)表示任意时刻,TKr中只能装有一种原油;式(5)表示炼油任务完成之前所有蒸馏塔持续炼油;式(6)表示任意时刻,至少有一个供油罐为DSk供油;本文中,在任意时刻,设为只有一个供油罐向DSk供油;式(7)保证了任意时刻TKr不能同时充油和放油;另外,供油罐充油完毕后,必须等待一段时间才能向外放油,以分离出原油中的海水,这段时间称为驻留时间约束。
2 可调度性条件
当系统执行某一 OD后,系统从状态Zl转换到状态Zl+1。为了保证原油的详细调度计划能够完成蒸馏塔的炼油计划,要求系统在时间域[0,∞)满足文献[9]所描述的可调度性条件。
Hou等[13]通过指派一系列的供油罐和蒸馏塔执行ODT和ODF,实现蒸馏塔的炼油计划。假设a时刻系统指派TKr和DSk,根据DSk的炼油计划、对应的原油库存以及以往的调度记录,可以确定DSk需要ODF和ODT转运的原油类型COT;为了减少蒸馏塔切换供油罐的次数,ODF和ODT取可以转运的最大油包体积V。

式中, ζki为DSk分馏i号原油的体积,Vki为a时刻已转运至供油罐的i号原油的体积以及初始时i号原油体积之和;totalk为a时刻可用于DSk分馏的总原油体积。ODT的起始时刻为a,结束时刻b=V/fpmax+a。ODF的起始时刻为totalk/fdsk,结束时刻为(totalk+V)/fdsk。
另外,当原油调度决策不选择供油罐或蒸馏塔,或者没有空闲的供油罐时,考虑停运状态,直至系统的可调度性边界再执行下一个调度决策。
3 BPGA算法
3.1 编码
图2为编码示意图, 决策变量X=(x1,x2,···,xm)表示1个粒子或者1条染色体,对应着1个原油详细调度计划。编码xn的取值范围在区间[0,1]内,n=1,2,···,m/2。其中,x2n−1、x2n为一组,分别为供油罐和蒸馏塔的编码。考虑到输油管道存在停运的情况,并且每次调度决策取尽可能大的油包V。因此,取决策变量X的编码长度m为

图 2 粒子/染色体编码Figure 2 Particle/chromosome coding

其中, ⌈∗⌉为向上取整函数;Cmin为 TK中容积最小的供油罐的容量;ξk,COT为DSk需要管道转运的COT号原油的体积。
3.2 解码
为了使种群具有更好的局部搜索能力,本文引入了混沌理论。混沌是存在于非线性系统中的一种普遍现象,混沌运动具有有界性、遍历性、随机性和对初值敏感等特点。混沌映射的数学表达公式为

式中,t为进化的代数;yt为第t代的出生数;µ为控制参数;当µ∈(3.569 94,4]时,映射处于混沌状态,T为迭代的代数。随机生成第1个出生数y1后,剩下的(T−1)个出生数根据混沌映射依次生成,得到一个长度为T的混沌序列。
决策变量X在解码前,需要根据混沌映射函数进行映射。混沌映射函数Hi(x)为

式中,Y(∗)=y∗;cei l( )为向上取整函数。X的编码xi通过混沌映射函数,找到混沌序列上相应的值Y(∗)。将X的编码依次映射后,得到映射后的X′为

某一时刻,根据以往的调度记录,可以得到需要管道转运原油的蒸馏塔集合 DS和空闲的供油罐集合 TK;根据 TK中供油罐的个数和 DS中蒸馏塔的个数,将连续的[0,1]分成若干个区间长度相等的实数槽,若X′的编码取值在某一槽中,就取槽对应编号的供油罐或蒸馏塔。例如某一时刻 TK有2个空闲的供油罐TK1和TK3,那么将[0,1]等分为2个实数槽,TK1的实数槽为[0,0.5],TK3的实数槽为(0.5,1],如果映射后的编码取值为0.6,那么,指派TK3执行ODT和ODF。类似地,根据X′的编码指派相应的DSk。
蒸馏塔在完成炼油任务前,至少需要有一个供油罐为其供油。那么,在调度周期[τs,τe]内至少有K个供油罐处于被占用状态。假设炼厂有H个供油罐可供使用,H≥2K+1,则在任何时刻,系统至多有H−K个空闲的供油罐。假设给定的系统初始状态为Z0,由于管道存在停运的情况,因此Z0至多有K(H−K)+1个种子状态。
当系统某一时刻根据X′的编码指派TKr和DSk执行ODT和ODF后,系统处于不可调度状态,系统需要通过回溯遍历,将不可调度状态纠正为可调度状态,其执行步骤如下。
Step1初始化管道输油速率fpmax、供油罐集合TK状态信息、原油驻留时间 Φ、蒸馏塔炼油速率fdsk以及炼油计划信息。
Step2判断系统的初始状态是否满足可调度性条件。是,执行Setp3;否,结束。
Step3根据X′的编码指派TKr和DSk执行调度策略。
Step4判断调度是否可行。否,标记当前策略已使用,修改编码,执行Step5;是,执行Step6。
Step5判断当前状态所有策略是否均已使用。是,弹出栈顶状态,并标记当前策略已使用,修改编码,执行Step5;否,执行Step3。
Step6当前状态进栈。
Step7判断是否完成炼油任务。是,结束;否,取下一组编码,执行Step3。
3.3 Pareto最优解集
对于一个多目标问题,其解集为 Set。任意2个解X1,X2∈Set且X1X2,M为优化的目标数量,以目标最小化为例,如果存在以下关系
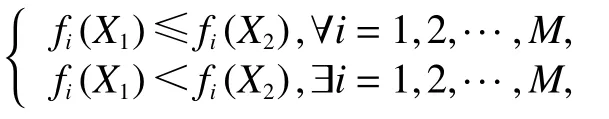
则称X1占优于X2。对于X∗∈Set,若解集 Set中不存在占优于X∗的解,则称X∗为问题的Pareto最优解。由所有Pareto最优解构成的集合,称为Pareto最优解集。Pareto最优解集在目标空间形成的曲面,称为Pareto前沿面(Pareto optimal front,PF)。
为了避免I-BBPSO的储备集中解的个数过少,I-BBPSO与NSGA-II都采用快速非支配排序算法(fast non-dominated sort,FNS)构造或更新Pareto最优储备集[14]。
3.4 种群更新
为了提高算法的全局搜索能力和局部搜索能力,本文提出基于I-BBPSO和NSGA-II的BPGA算法,协同搜索原油详细调度问题的Pareto最优解。
骨干粒子群算法(bare bone particle swarm optimization,BBPSO)是由Kennedy[17]提出的,粒子的位置通过高斯采样进行更新。为了保证算法后期的收敛性,本文引入模拟退火算法p(t),采用以下改进的位置更新公式。

粒子群中的每个粒子记录着其目前所找到的最优解。该高斯采样公式保证粒子始终在其个体引导者和全局引导者之间运动,使得粒子朝着一定的方向探索,可以保证粒子的全局搜索能力。
NSGA-II储备集中每个个体都有相应的适应度,较优的个体适应度较大。算法的思想是:首先随机选择种群中的2个个体,适应度越大的个体被选择的概率越大,然后按照一定的概率使染色体交叉和变异,从而产生子代种群。
NSGA-II算法能够保存种群中的较好个体,并使种群能够朝向一定的方向进化。
3.5 移民策略
为了使BPGA具有较好的多样性,防止算法过早陷入局部最优,BPGA采用移民策略实现2个种群的协同计算,并且引入种群差熵,动态控制种群进行移民操作。
3.5.1 种群差熵
对于双种群进化算法,以往的思路是通过手动调节参数来控制种群移民操作,将源种群中的最优个体代替目标种群中的最差个体,实现多种群协同进化。本文通过引入种群差熵[18]的方法实时监测当前种群的多样性。种群差熵的计算公式为
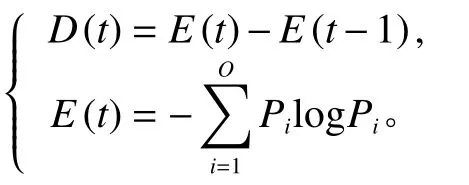
式中,E(t)为种群在第t代时的Pareto熵;D(t)为第t代种群与上一代种群的Pareto差熵;O为种群中不同个体的数量;Pi表示目标值相同的个体在种群中的概率。
3.5.2 移民操作
Cmax是一个固定的常数。Pop1、Pop2分别为IBBPSO、NSGA-II的储备集。当I-BBPSO或者NSGAII新生种群的差熵不大于0的次数达到Cmax时,取出2个种群的储备集中一定比例的最优个体,与另一个种群的储备集合并,然后经过快速非支配排序FNS后,得到更新的储备集Pop1、Pop2,实现种群间的交流。
3.6 BPGA的算法流程
Step1初始化种群。首先随机生成N个决策变量X1-XN,解码后得到N个个体;然后将个体1−N/2、(N/2+1)−N分别进行快速非支配排序FNS后,放入Pop1、Pop2中。2个储备集的大小均为N/2。cnt1、cnt2均为0,分别用于统计D1(t)和D2(t)小于0的次数。
Step2种群更新。I-BBPSO、NSGA-II更新储备集得到新种群R1和R2,分别与Pop1和Pop2合并后,经过快速非支配排序FNS,得到更新后的Pop1和Pop2。
Step3计算Pop1、Pop2的种群差熵D1(t)、D2(t)和cnt1、cnt2。
Step4cnt1或 cnt2是否等于Cmax。 是,进行移民操作,等于Cmax的计数器置0;否,执行Step5。
Step5是否满足结束条件。是,将Pop1和Pop2合并,经过快速非支配排序FNS后得到大小为N的Pareto最优解集E;否,执行Step2。
4 算例分析
图3为中国南部某炼油厂的一个10 d炼油计划,该炼油计划共有3个蒸馏塔DS1∼DS3,以及10个供油罐TK1~TK10。
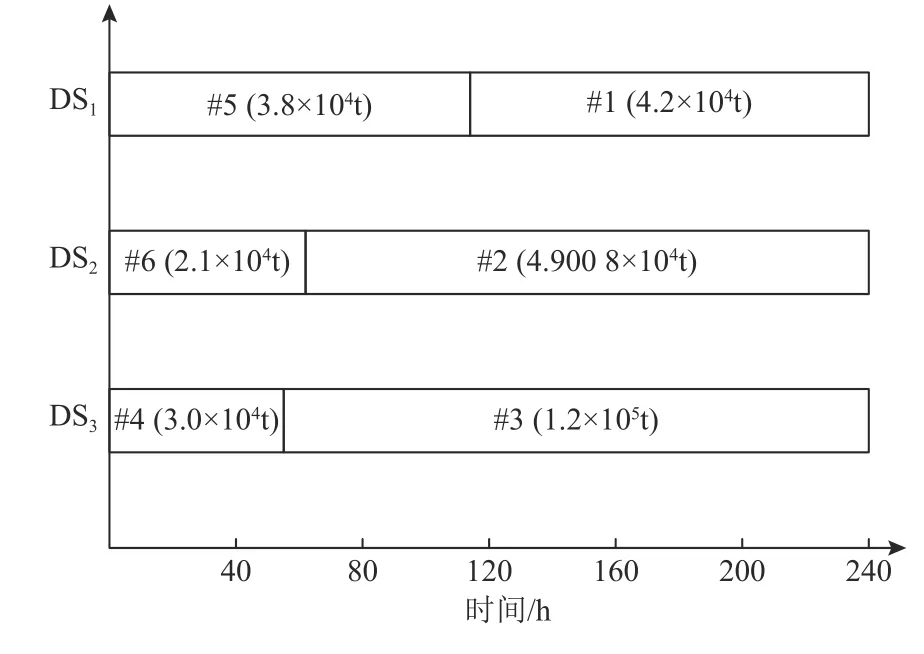
图 3 蒸馏塔10天炼油计划Figure 3 The distiller feeding schedule for 10 days


表 1 供油罐初始状态信息Table 1 The initial status information of charging tanks

为了说明BPGA的性能,将BPGA与多目标骨干粒 子 群(bare-bones multi-objective particle swarm optimization, BB-MOPSO)算 法[19]、多 目 标 粒 子 群(multiple objective particle swarm optimization,MOPSO) 算法[20]、NSGA-II和NSGA-III[21]等4种算法进行实验对比。实验均基于PlatEMO[22]平台,采用Matlab编程实现。实验环境为Intel(R) Core(TM)CPU 1.8 GHz 4.00 RAM,Windows 7。对于每组实验,独立重复执行30次,取平均值。
在求解实际问题时,通常问题的PF前沿面是未知的。在实际的实验中,通常通过收集所有运行的数据构造问题的PF前沿面,然后通过最大−最小标准化的方式将数据归一化。Zitzler等[23]采用(hypervolume,HV)指标评价多目标进化算法的多样性和收敛性的综合性能。假设解集 Set为非支配集,本文选定参考点为(1,1,1,1),解集 Set的HV指标值为由解集 Set中所有点与参考点在目标空间中所围成的超立方体的体积。因此,算法求解问题得到的HV值越大,算法的综合性能越优。本实验中种群大小Size为250,由图4可以看出,当评价次数超过10 000次后,5种算法的HV值趋于稳定,BPGA算法的综合性能较优。
Zhang等[24]采用C指标评价多目标进化算法得到解的质量。其公式为

图 4 5种算法的HV指标Figure 4 HV indicator of five algorithms

式中,u为算法B迭代后储备集中的个体;v为算法A迭代后储备集中的个体;分子为算法B迭代结束后储备集中被算法A中储备集的解占优的解的个数;分母为算法B储备集中解的个数。因此,当C(A,B)>C(B,A)时,说明算法A储备集的解的质量更高。 表2中,A为BPGA,B为对比算法。从表2看出,在列出的5种算法中,BPGA求得的Pareto最优解的质量更优。

表 2 5种算法的C指标Table 2 C indicators of five algorithms
另外,本文算法与文献[13]实验结果相比,不仅能得到更多的非支配解,同时部分非支配解占优于其中的部分支配解。表3和表4列出详细的各个非支配解的各个目标函数值。表3中方案1、6与表4中方案1、5所对应的Pareto最优解相等;表3中方案2、3、5所对应的Pareto最优解要优于表4中方案2、3、4、6所对应的Pareto最优解。从以上数据可以看出,BPGA在求解原油一次加工过程多目标优化问题时,具有较优的性能。值得注意的是,算法得到最终的Pareto最优解集后,决策者需要根据实际情况选择最适合的生产调度计划。表4中,当设备维护致使供油罐不足时,必须牺牲其他成本以保证生产连续稳定进行,此时应选择方案6;当供油罐充足时,可以选择方案1以最大限度降低其他成本。

表 3 BPGA多次迭代获得的非支配解的各个目标函数值Table 3 The objective function values of the non-dominated solutions obtained by BPGA algorithm

表 4 文献[13]中得到的Pareto最优解集Table 4 Pareto optimal solution set obtained in the literature [13]
5 结束语
为了降低原油处理过程短期生产计划问题的复杂性,本文把该问题分解为上下2层:上层求解一个目标炼油计划以获得最大生产率;下层求解一个详细炼油计划以实现上层目标炼油计划。上层目标炼油计划相对来说比较容易得到,但其下层详细生产调度的获得十分困难。本文在已有文献将下层详细调度问题转化为供油罐到蒸馏塔的指派问题的基础上,探索求解下层详细调度过程中多个优化目标的Pareto最优解的新方法。为了提高多目标进化算法的多样性和收敛性,本文提出一种基于I-BBPSO和NSGA-II协同计算的双种群进化算法BPGA。与传统的单种群进化算法相比,BPGA具有更好的收敛性和多样性,同时能获得质量较优的解,且具有调节参数少、能根据种群状态自动维护种群多样性等优点。本文算法在求解原油一次加工过程的详细调度时,能够向决策者提供多种Pareto最优的详细调度计划,在实际的炼油生产中,对提高企业的利润具有重要的现实意义。

