考虑电量消耗的车辆调度优化研究

王 泽，杨信丰，刘兰芬

(兰州交通大学 交通运输学院，甘肃 兰州 730070)

随着社会经济不断进步，电商的发展极大地促进了快递行业的发展。“绿色物流”也逐渐受到更多快递企业的重视，国内一些快递公司开始逐步尝试使用纯电动汽车作为配送车辆，来完成从配送中心到客户的配送任务。相较于传统燃油汽车，新能源电动车具有环保、节能、噪声污染小等优势，新能源电动汽车可以更好地为整个社会创造经济效益和社会效益。但是电动车在配送过程中需要考虑载重量、里程、充电需求等约束，使得配送问题更加复杂。

国内外部分学者对电动车调度进行研究，并取得了一定的成果，如Schneider等[1]考虑电池容量、服务时间等约束，提出成本最优的电动车路径规划和调度模型，采用混合启发式算法对模型进行求解，计算结果能较好地反映出电动车的行驶路径和充电决策。Haghain等[2]利用遗传算法求解时间依赖型车辆调度问题，将求得结果与精确算法计算结果进行比较。Desaulniers等[3]对电动商用车(ECV)车队进行路径规划时，考虑4种情况下带时间窗的电动车辆路径规划问题，结合算例验证算法的优越性。Bruglieri等[4]利用可变邻域搜索分支的算法解决带有时间窗的电动汽车路径问题。高升[5]采用遗传算法解决以总配送成本最小为目标的考虑客户时间窗的电动汽车路径优化问题模型。杨珺等[6]设计禁忌搜索−改进clarke-wright节省的两阶段启发式算法，研究基于电动汽车物流配送网络的换电站选址与路径优化问题。邵塞等[7]以费用最小化为目标，考虑电动汽车的里程、载重、时间窗等约束，用遗传算法解决电动汽车集散货一体化车辆路径问题模型。张艳伟等[8]以总成本最小为目标，建立纯电动汽车运营的考虑货物类别的路径优化问题。揭婉晨等[9]利用列生成的分支定价算法解决基于时间窗的电动车车辆路径问题。王永聪[10]在研究车辆路径问题的基础上，建立以城市配送为目标的纯电动汽车车辆路径模型，并应用最邻近算法和蚁群算法对其模型进行求解研究。刘兰芬等[11]在考虑时间网络的基础上，建立以客户满意度最高、配送时间最短等多目标物流车辆调度模型，并用遗传算法求解该模型。陶胤强等[12]以最小费用为目标，研究基于时间窗的多车型多费用非满载的车辆路径问题。梁凤婷等[13]研究低碳环境下电动汽车的车辆路径问题，以低碳、节能环保和低成本为目标，建立燃油车和电动车的车辆路径模型，并用遗传算法对模型进行分析和求解。

从研究现状可知，国内外学者对纯电动汽车调度方案的研究成果相对较少,针对具有时间窗的车辆调度问题研究较多，主要采用智能算法求解车辆调度方案，如遗传算法、蚁群算法、模拟退火算法等。鉴于此，本文着重考虑单向车辆调度模型，重点考虑时间窗约束、里程约束及充电需求，提出电动汽车基于电量消耗的车辆调度模型，合理规划包括配送方案、车辆行驶路径、车辆发车时间及车辆充电计划在内的车辆调度方案。

1 问题描述

由于电动汽车是靠电能驱动，故充电是电动汽车在行驶过程中必须面对的问题之一。当电池电量不足以完成剩余的配送任务时，电动车需要进入到邻近的充电站进行充电，以供其完成剩余的配送任务。在本文中，充电站采用的是快速充电方式，使电动车在30 min左右就可以完成充电。但是由于充电站可能不位于车辆既定的行驶线路上，车辆会发生行驶偏移，因而带来配送中心总成本的增加。

由于电动车配送过程需要考虑电动车的续驶里程、电池电量、充电站位置、客户服务的时间窗和车辆额定载重等诸多因素，为使问题更加简洁明了，预先进行以下假设。

1) 只有一个配送中心，所有车辆从配送中心出发最后返回原配送中心；

2) 客户的数量、客户的位置、客户服务的时间窗及每个客户的需求量均已知，且车辆的总载重不得超过车辆的额定载重；

3) 配送车辆从配送中心出发，电池为满电状态，且在货物装卸过程中不存在电量的消耗；

4) 货物流向为单向，只进行配送货物不进行收集货物；

5) 电动车的额定续驶里程和充电时间均已知。

2 模型建立

2.1 符号及变量定义

C0为总费用；

Cfk为车辆k的固定费用；

Ctk为车辆k的行驶费用；

Cmk为车辆k的充电费用；

Cpk为车辆k的早到或晚到产生的惩罚费用；

O为配送中心；

K为车辆集合；

M为充电站集合；

N为客户点集合；

L为配送中心、充电站、客户点的集合，L=O∪M∪N；

speed为车辆额定行驶速度；

P为电动车额定电量；

为车辆k到达集合点i时电量，i∈L；

为车辆k离开集合点i时电量，i∈L；

ei为客户点i的最早服务时间；

li为客户点i的最晚服务时间；

epu为表示车辆早于时间窗到达造成的等待惩罚成本；

lpu为表示车辆晚于时间窗到达的惩罚成本；

为车辆到达集合点i的时刻，i∈L；

为车辆离开集合点i的时刻，i∈L；

为车辆在集合点i卸货、充电时间，i∈L；

为车辆在客户点处等待服务时间，i∈N；

Djk为车辆k到达点j时的剩余电量里程；

di j为客户点i和j之间的距离；

Wmax为车辆额定载重量；

Dmax为车辆最大行驶距离；

Ed为电动车电量单位里程消耗；

Wi为车辆载重量；

2.2 配送过程分析

1) 总成本分析。总配送成本包括4部分。

(1) 车辆固定成本。固定成本主要包括车辆折旧费，司机劳务费，餐饮费等。

(2) 车辆行驶费用。行驶费用与行驶距离相关，车辆单位行驶成本为

(3) 充电费用。充电费用的多少与电池剩余电量相关，剩余电量越高，则充电费用越少，充电时的单位充电成本为c2，Cmk=EdS c2，S为匀速行驶里程。

(4) 惩罚成本。惩罚成本主要由车辆早于或晚于客户服务时间窗而引起，车辆早于服务时间窗到达需等待，等待时间为ei−，车辆晚于服务时间窗到达，客户需要等待的时间为−li，则总惩罚成本为

2) 电量分析。

假设该电动车行驶过程为匀速状态，那么，根据文献[14]提出的能耗经济性评价指标，本文提出纯电动汽车在匀速行驶状态下电池电量的单位里程能耗为

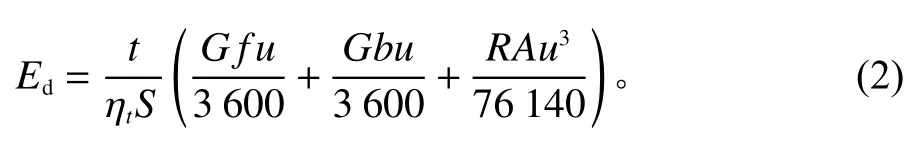
其中，G为 车辆重量；t为纯电动车匀速行驶时间；b为道路坡度；u为车速； ηt为传动系统效率；f为滚动阻力系数；R为空气阻力系数；A为汽车迎风面积。电动车从点i到达点j(i,j∈L)的剩余电量为Pik=P−Eddij。

3) 车辆在各点停留时间分析。

，i∈L。若i表示客户点，则其表示车辆在该点的卸货时间；若i表示充电站，则其表示车辆在充电站的充电时间；若i表示配送中心，则停留时间为0。

4) 车辆等待时间分析。

，i∈N。若车辆提早到达客户点N，则要等待，等待时间为若在规定时间内到达，则不需要等待，等待时间为0。

5) 车辆到达客户点时刻分析。

电动车辆从客户点i离开，到达客户点j的时刻为电动车离开客户点i的时刻加上车辆在客户点i和j之间的行驶时间，即

2.3 数学模型

根据上述分析，构建考虑电量消耗的电动汽车调度优化模型如下。

式(4)为模型的目标函数，保证总成本最小；式(5)~式(15)均为模型的约束条件。其中，式(5)保证每一位顾客都只被服务1次；式(6)保证车辆开始完成配送任务从配送中心出发和结束；式(7)保证在客户点卸货过程中不消耗电量；式(8)表示电量足够到达集合L中 的任意点；式(9)表示车辆在点i和点j之间的行驶时间；式(10)表示车辆离开集合点i的时间；式(11)表示车辆到达集合点j的时间；式(12)表示车辆实际载重量不超过额定载重量；式(13)表示车辆若提早到达集合点i的等待时间；式(14)表示决策变量是0−1变量；式(15)表示惩罚成本函数。

3 算法设计

车辆路径问题属于NP-hard问题，该问题约束条件繁多，规模较大。遗传算法具有强大的搜索能力和自适应性，因此遗传算法对于求解较为复杂的大型网络车辆调度问题具有较好的效果。本文选用遗传算法求解电动汽车调度方案模型。

3.1 染色体结构设计

本文采用自然数编码的方式[5]，将染色体长度定义为足够大(2n+1)，其中，n为顾客的个数；m表示充电站的个数；k表示配送中心的车辆数。将配送中心的编号设定为0，n位客户的编号分别设定为1,2,3,···,n，可以将m个充电站的编号分别设定为n+1,n+2,···,n+m。最后在起点和终点分别插入配送中心代码0，即构成1条染色体。例如，某配送中心为5位顾客提供服务，配送区域有1个充电站，假如其中1条如图1所示，则该染色体表示的路径为第1辆车从配送中心出发，先后经过客户点3、4，然后进入充电站6进行充电，充电完成后返回配送中心，第2辆车经过客户点1、2、5返回配送中心。

图 1 路径染色体路径Figure 1 Path of chromosome

3.2 种群初始化

首先将所有客户与充电站的编号进行随机排列，设wi表示各点的需求量，然后考虑每辆汽车的载重约束，若则在染色体第γ 位后插入编号0，重复计算直至考虑完所有客户的需求量约束，再考虑充电需求，若里程不足需求充电时，在该客户点后插入最近的充电站编号，直至判断完所有客户的里程约束。最后在起点和终点分别插入配送中心代码0，即构成1条染色体。重复多次计算，即构成初始种群popsize。

3.3 适应度评价

对种群中的每条染色体进行解码，解码后可得到每条染色体下的路径，但是车辆的发车时间没有确定，再用遍历法选出各辆车最适宜的发车时刻。具体思路如下。在配送中心的运营时间6:00~21:00内，按每间隔10 min发车，计算总配送成本。最小配送成本的发车时刻即为最优的发车时刻。若存在多个最优发车时刻，选取本时间段内时间最小的时刻为发车时刻。根据上述求得每条路径的总配送成本，可将目标值的倒数定义为对应染色体的适应值：Zi=1/C0。适应度值作为个体性能的评价指标，其值越大，配送总成本越低，越接近最优解。

3.4 种群更新

1) 选择。

本文采用最佳个体保存和适应度比例相结合的方式来对染色体进行选择[15]，将每代个体中的H个染色体按其适应度值从大到小依次排列，排在第1位的即是适应度值最大的，将其直接复制到下一代当中，对于下一代中其余的H-1个染色体则采用轮盘赌的方式来产生。这样的选择方式既能保证适应度最大地进入下一代，也能使适应度值较大的有机会进入下一代。

2) 交叉。

本文采用部分匹配交叉(PMX重组)方式，先对群体随机配对，产生1对染色体(父代)，2个染色体被选的位置相同，交换这2组基因的位置，最后进行冲突检测，删除染色体中重复的基因，保证基因不重复。该方式能较好地保持群体多样性。选取2个父代染色体A和B并随机生成2个交叉点，把2个交叉点之间的基因片段替换为对方染色体，得到A1和B1。可从图2(b)中看出基因之间的对应关系：基因3、5和4相互对应；基因1和6相互对应。然后再替换掉交叉点之前和交叉点之后基因片段中重复的基因，如将染色体A1中交叉点后重复的基因1、5分别替换为与其对应且不重复的基因6、4，对染色体B1同样处理，即可得到染色体A2和B2，具体过程如图2所示。

3) 变异。

本文采用基因片段反转变异的变异策略[16]，此策略在排序问题方面性能较优，优于传统的对换变异等策略。选取任意染色体A并在该染色体上随机生成2个交叉点，把2个交叉点之间的基因片段进行翻转即可得到变异后的染色体A',具体如图3所示。

图 2 染色体交叉示意图Figure 2 Chromosome for crossover

图 3 染色体变异示意图Figure 3 Chromosome for mutation

4) 终止策略。

若此时的迭代次数小于初始规定的总次数，则返回至上述步骤，继续进行迭代；若此时迭代次数等于初始规定的迭代总次数，则对最后一代的染色体进行解码操作。此时即可得到该车辆调度问题的近似最优解，又可同时得到配送中心车辆的配送路线和配送中心总成本。

4 案例及结果分析

设某配送案例中，有1个配送中心，4个充电站，充电时间为0.3 h，5辆相同型号的配送车辆共服务50个客户。且配送中心、充电站、客户的坐标、客户点需求和服务时间窗均已知。车辆从配送中心出发，考虑到有充电需求，所以应合理安排路径，完成配送任务。车辆详细参数如表1所示，配送过程中各项成本如表2所示，实例中各客户的信息如表3所示。

表 1 某电动货车能耗计算相关参数Table 1 Relevant parameters of energy consumption calculation of the electric truck

终止条件为Genmax=1 000，种群大小NP=40，交叉概率pc=0.8，变异概率pm=0.3。为避免结果出现偶然性，本文直接使模型重复计算10次，选取10次中配送总成本最小的作为最优值。经过计算，车辆的最佳配送路径和遗传算法迭代图如图4、图5所示，成本及路线结果如表4所示。此时，线路上最优成本为2 266.158元，5辆车共6次进入充电站进行充电，其中充电成本共计80元，车辆固定成本为500元，车辆行驶成本为1 686.158元，得到最优配送路径后，再用枚举法考虑顾客的服务时间窗，计算在配送中心运营时间内各车辆的最佳发车时间。求得第1辆配送车辆的发车时间为6:00，惩罚成本为208.38元；第2辆配送车辆的发车时间为6:00，惩罚成本为364.21元；第3辆配送车辆的发车时间为6:00，惩罚成本为170.18元；第4辆配送车辆的发车时间为6:00，惩罚成本为148.41元；第5辆配送车辆的发车时间为9:30，惩罚成本为4.65元。此时配送中心考虑惩罚成本后的总配送成本为3 161.99元。每辆车的最佳发车时间及到达顾客和充电站的时间如表5所示。

表 2 配送过程各项成本Table 2 Cost of the distribution process元

5 结论

本文基于电动车电量特性，充分考虑电动车电量消耗、里程约束、载重约束、顾客服务约束等，建立以配送总成本最小为目标的基于电量消耗带时间窗的电动汽车路径规划问题模型，对模型中配送中心总成本、电动车电量的单位里程能耗、电动车停留时间、电动车行驶时间等进行分析；采用遗传算法首先求解出该模型中配送车辆的最佳配送方案，该配送方案包括车辆的行驶路线和行驶过程中的充电计划，再结合枚举法在配送中心运营时间内以10 min为时间间隔，优选出配送车辆惩罚成本最小时的最优发车时刻，从而得到车辆到达每一客户点及充电站的时刻。最后结合算例，计算出最佳配送路线、充电方案、最优发车时刻以及最小总配送成本，验证了该模型和算法的有效性和正确性。但本文只研究了基于时间窗的电动汽车调度问题，而现实生活中，道路实际情况，以及顾客的服务需求都是动态变化的。如何根据实际的动态要求，将是今后进一步研究的内容。

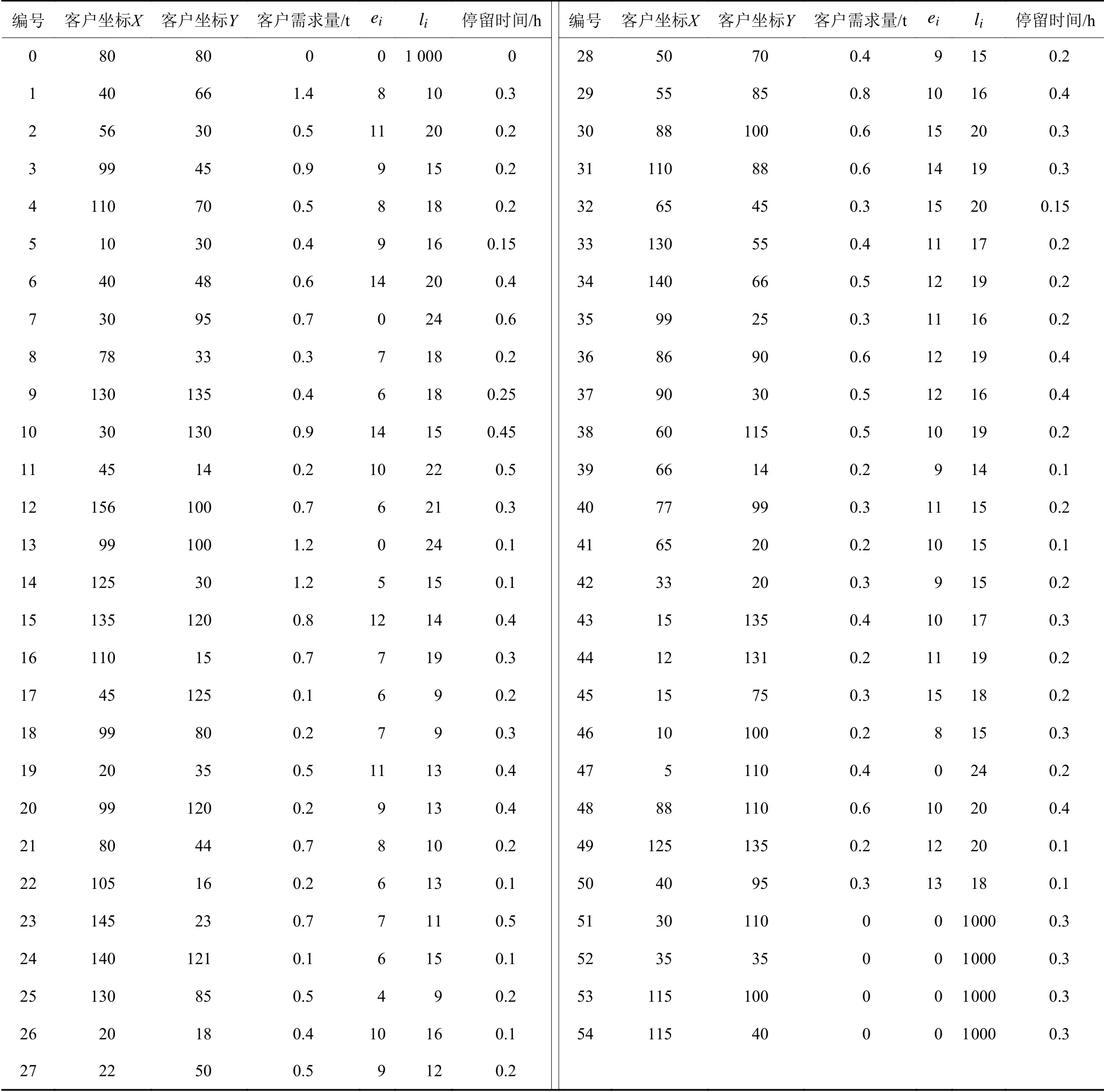
表 3 算例数据1)Table 3 Data of example

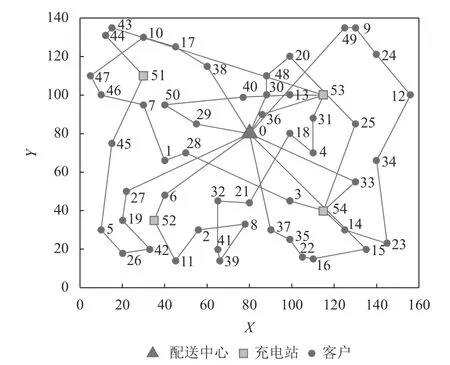
图 4 车辆配送路径Figure 4 Vehicle delivery path

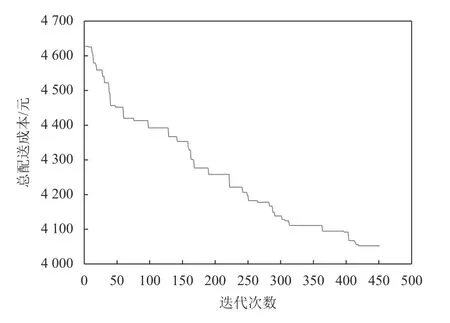
图 5 遗传算法迭代过程示意图Figure 5 The iteration process diagram of genetic algorithm

表 4 计算结果Table 4 Results of calculation

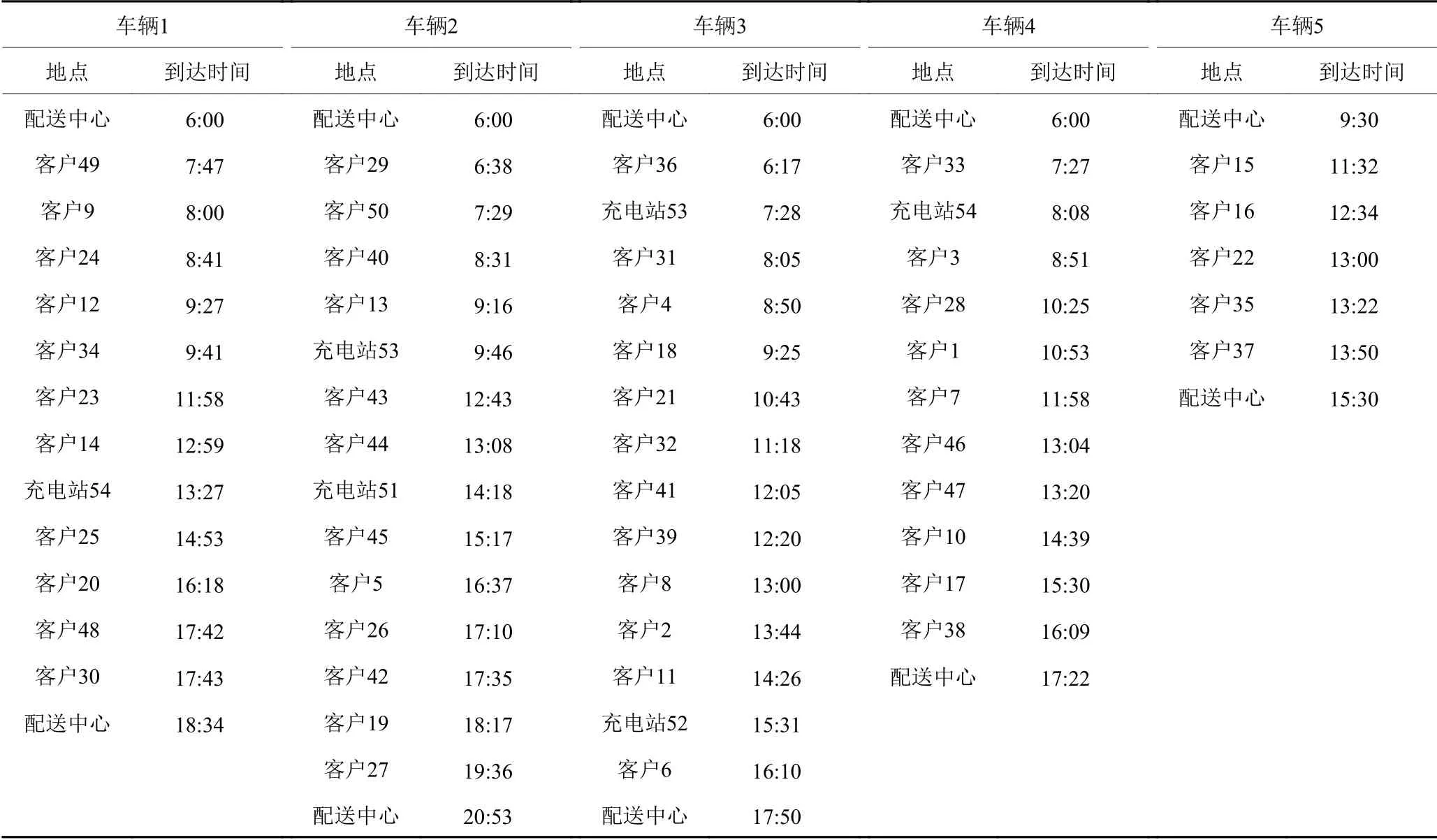
表 5 客户配送时刻表Table 5 Customer delivery schedule