关联交叉口间高饱和度路段排队长度研究
徐建闽,李鑫,邹磊,马莹莹
(华南理工大学土木与交通学院,广东广州510640)
0 引言
随着城市机动车保有量的不断攀升,高峰期路段常出现周期性的长距离排队,甚至排队溢出至上游交叉口,影响通行效率,造成路口瘫痪。路段排队长度模型的研究是路段溢流控制的重要前提,常见的排队模型有三类:概率模型、输入输出模型和冲击波理论。
概率论模型通过假设交通流到达和离去所服从的概率分布来估排队长度,常用于独立交叉口排队研究[1];输入输出模型通过累计所有到达和离开的车辆数来计算排队长度,构造较为复杂;冲击波理论假设车流为稳定的流体,冲击波定义为两种不同流量—密度状态车流的时空边界,通过追踪波运动轨迹来分析车辆排队的形成和消散,被广泛使用于交叉口排队长度[2]、路段延误[3]和相位差优化[4]研究。车流行驶过程中车流的离散性,导致冲击波传播轨迹难于计算。现有研究中通常使用交通检测方法来提高模型鲁棒性和精确度的关键:一是安置线圈检测器来识别上游到达排队车辆排队和释放状态的改变[5-6],进而获取冲击波,羊钊等[7]提出了冲击波检测器的布设位置,在此基础上提出最大广义排队长度计算模型,姚荣涵等[8]以路段检测器所得车头时距数据区分车流,并得到不同车流的流量—密度特性,构建了以此为输入参数的车辆排队模型;二是基于视频处理技术动态获取排队信息,曹倩霞等[9]基于视频处理技术利用虚拟平行线定位每车道排队车辆首尾端,并结合排队首尾车的跟踪与停车线处虚拟线圈的计数来检测排队车辆数;仕小伟等[10]通过视频检测器获取路段的实时排队长度,结合冲击波理论和累积的输入输出方法,提出了的交通溢流发生机理模型。
但在排队长度较长的高饱和度的路段,传统的交通检测方法存在难以克服的难度和缺陷:线圈检测器的铺设存在选位合理性问题和精度问题,排队超过检测器时,检测器将难以通过流量—密度变化来识别车流状态的改变;视频检测则存在外物遮蔽以及可视范围的问题[11]。现有研究表明,高饱和度下车流速度具有趋于一致、离散型较小的特点,路段车辆多以车队的形式运行[12-13]。本文基于此特点,采用冲击波理论对高饱和度路段的排队模型进行研究。
1 路段排队长度模型
1.1 研究路段说明
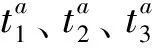
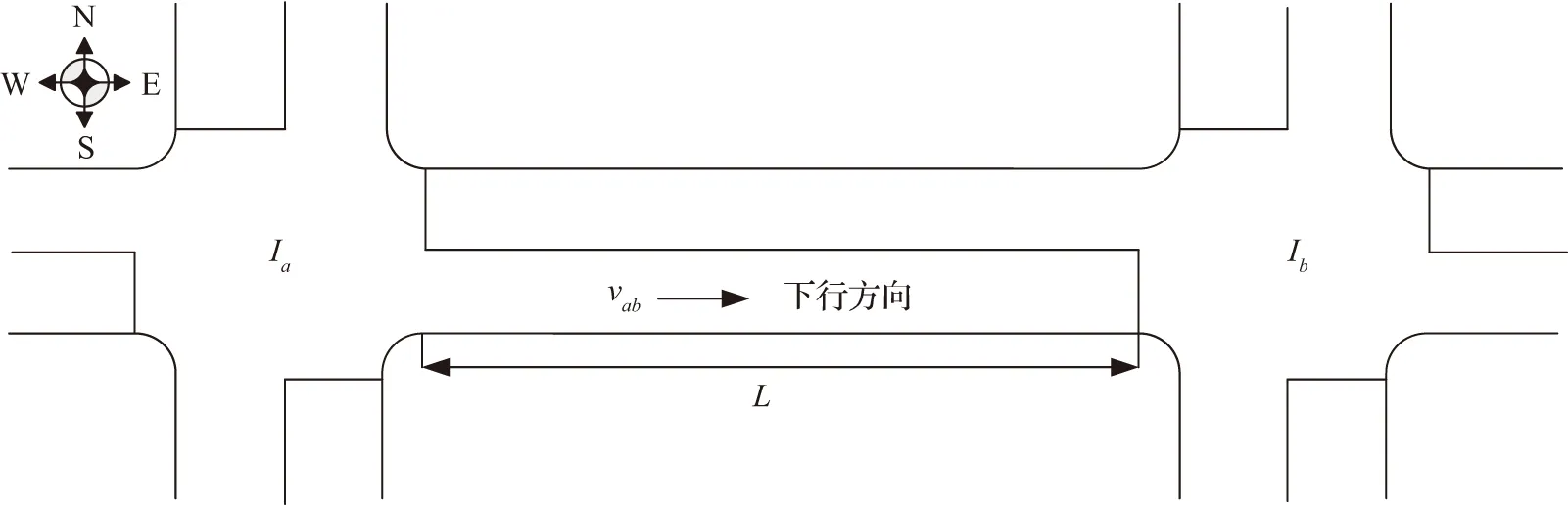
图1 路段及交叉口位置示意图Fig.1 Section and intersection location
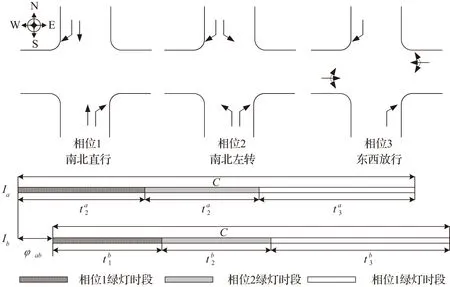
图2 路段及交叉口相位设置示意图Fig.2 Schematic diagram of section and intersection phase setting
1.2 路段排队模型分析
1.2.1 初始周期排队模型
初始周期排队情形见图3。

(a) 排队未溢出
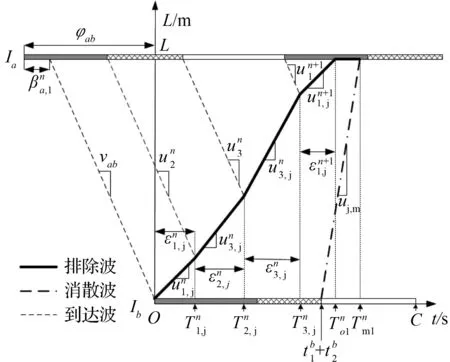
(b) 排队未溢出

(1)
(2)
(3)
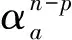
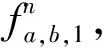
①路段排队未溢出。
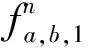
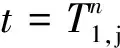
(4)
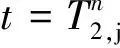
(5)
(6)
(7)
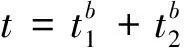
(8)

(9)
②路段排队溢出。

(10)
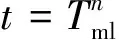
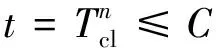
(11)
综上,得第n个周期内路段IaIb无溢出时的排队模型,有:
(12)
1.2.2 后续周期排队模型
后续周期排队受到初始周期是否存在二次排队的影响,以“1.2.1初始周期排队模型”分析为基础,根据是否有二次排队,对后续周期排队情形进行分析:
①初始周期无二次排队。
(13)
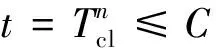
(14)
此时,初始周期排队车辆完全清空,后续周期排队不受初始周期影响,后续周适用初始时刻t=C,初始距离为l=0的初始周期排队长度—时间模型。

(a) 后续周期排队未溢出
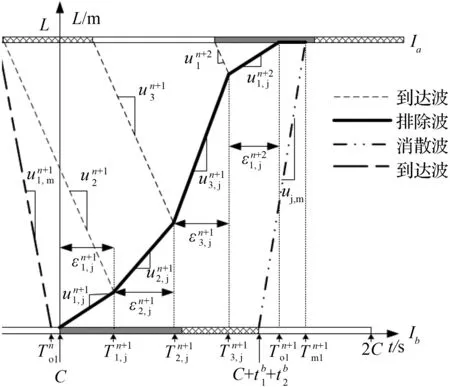
(b) 后续周期排队溢出
②初始周期有二次排队。
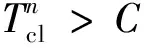
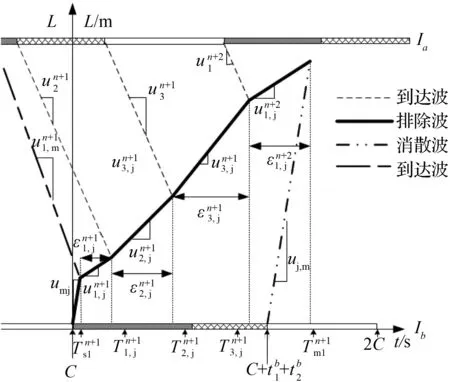
(a) 后续周期排队未溢出

(b) 后续周期排队溢出
t=C时,交叉口Ib相位1红灯起亮,停车线后车流由消散状态(qm,km)转变为停车状态(0,kj),产生波速为um,j的排队波向Ia传播。
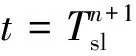
(15)
2 模型适用性验证
2.1 仿真实验设计
(16)
以0.02为间隔在0.40~0.90的范围内设置25组不同λa,b的流量组合作为流量输入,以0.01为间隔在在0.90~1的范围设置10组。

2.2 模型输入参数设置

(17)
模型参数输入情况见表1。

表1 模型参数输入情况Tab.1 Model parameter input
2.3 模型验证
(18)
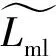
(a) 最大排队长度误差分布
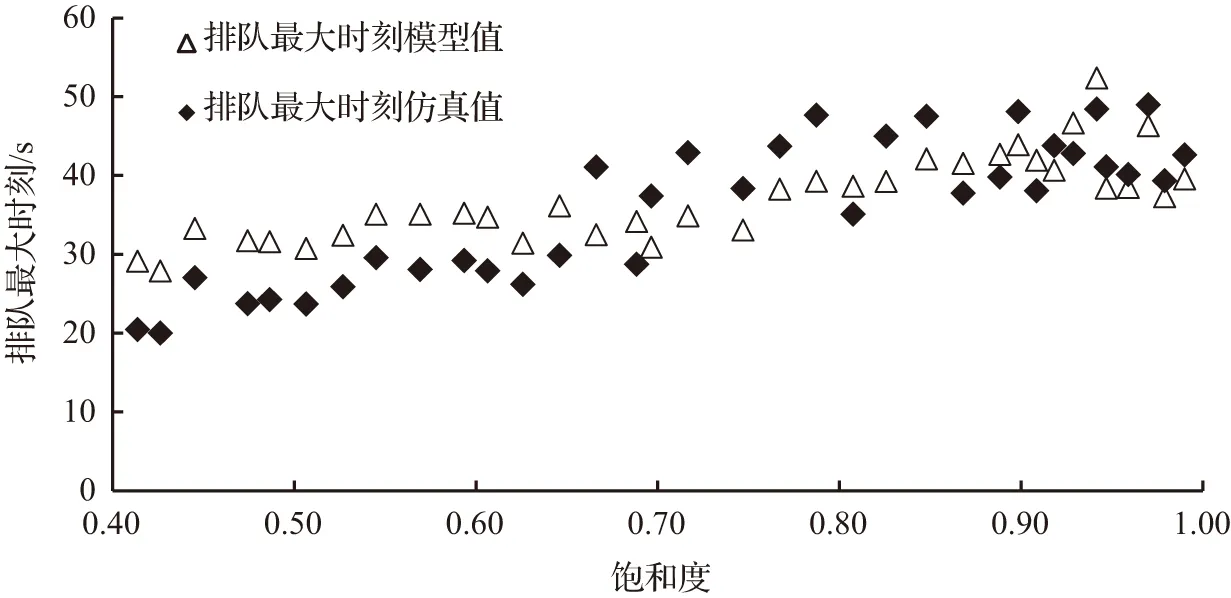
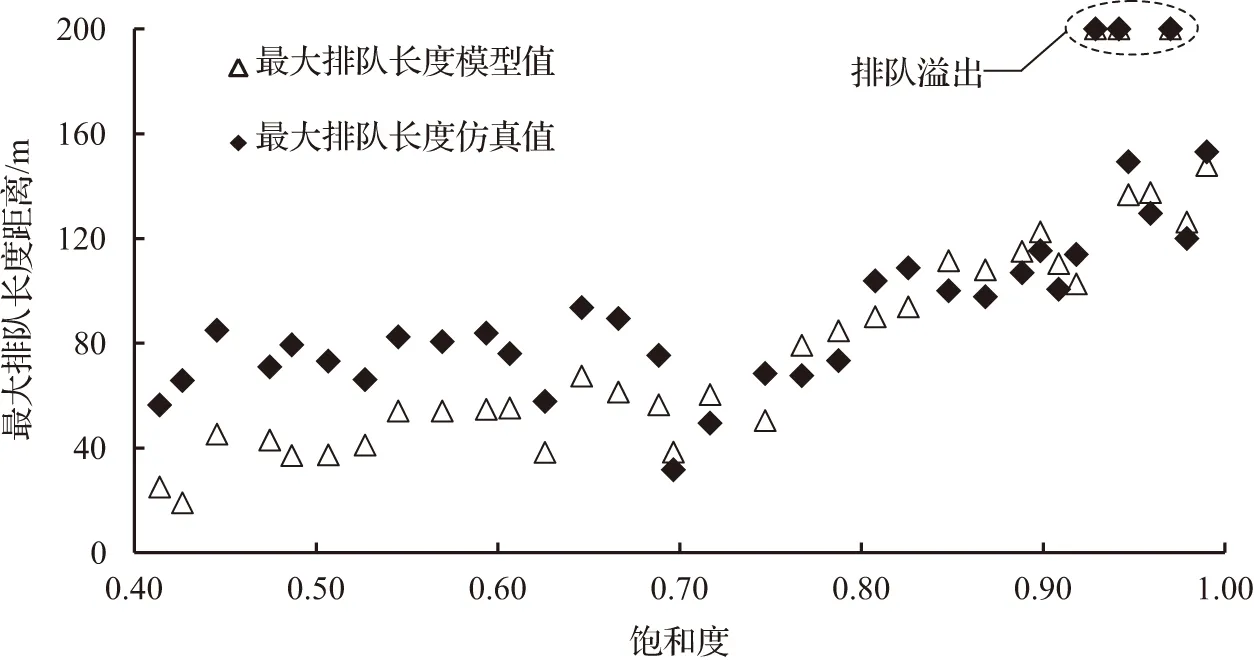
(b) 排队最大时刻误差分布
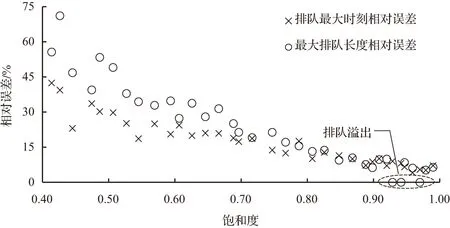
图7 不同饱和度下模型值与仿真值相对误差分布Fig.7 Relative error distribution of model value and simulation value under different saturation
3 相位差对排队长度的影响
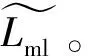
由图8所示,其他参数固定时,红灯相位差φa,b,1决定了车流到达顺序及排队波的产生顺序,同一波速的排队波在初始时刻产生相比后续产生,能传播更长的时长。当上游驶入车流流量差异较大时,所形成的排队波波速存在较大差异,红灯相位差对最大排队长度有一定的影响。
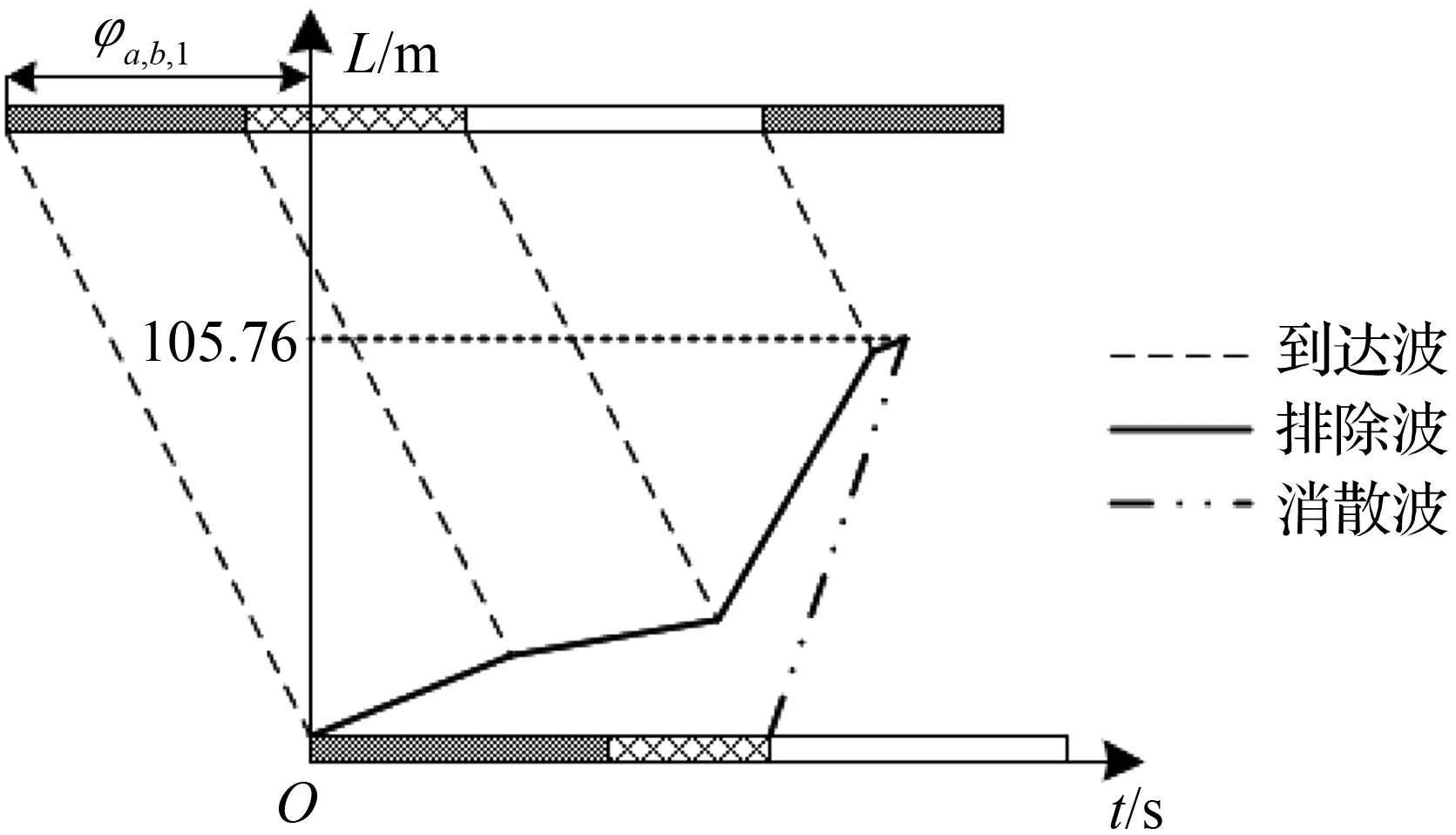
(a) 0≤φa,b,1≤15 φa,b,1=59
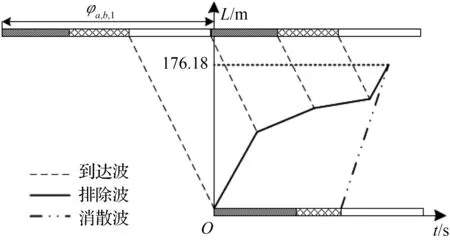
(c) 40≤φa,b,1≤58
4 结论
本文针对城市协调交叉口间路段周期性排队问题,论述了冲击波传递轨迹与路段排队增长情形,建立了排队长度模型,通过VISSIM仿真验证,结果表明:路段饱和度较高时,模型计算的最大排队长度、排队最大时刻较为精确,最后,基于模型分析了相位差对于路段最大排队长度的影响,为利用相位差进行溢流控制提供理论基础。
本文所提出的排队模型不仅仅适用于仿真实验中的单车道,对于下游交叉口采用进口单放的多车道路段同样适用。此外,模型能以周期为间隔输入,上游交叉口各相位的动态流量数据,从而实现路段排队长度的实时预测。

