2050年上海大都市圈海平面上升影响预估研究
宋苑震,覃盟琳*,朱梓铭,黎航
(1.广西大学土木建筑工程学院,广西南宁530004;2.广西大学人居环境设计研究中心,广西南宁530004;3.印第安纳州立大学地球与环境系统学院,印第安纳州特雷霍特47807)
0 引言
随着全球气候变暖,海平面上升加快,预计到2100年,全球将有90 %的沿海地区受到海平面上升影响[1]。海平面上升,将一定程度上放大、加强海平面上升淹没、风暴潮、洪涝影响、海岸侵蚀以及海水入侵等现象的强度,对沿海地区经济社会发展、生态安全和城市发展建设产生负面影响[2]。
国内外学者在海平面上升对沿海地区相关影响上进行了较多研究,研究主要集中在以下几个方面:①研究方法上,提出海岸带脆弱性指数[3]、改进的SPRC模型[4]等用来预测海平面上升高度;②所用数据上,利用沿海台站数据[5]、IPCC公告[6]、中国海洋公报[7]、遥感数据[8]等数据分析相关影响;③研究对象上,多集中在沿海湿地脆弱性[9]、海平面上升淹没[10]、沿海红树林[11]、河口三角洲[12]等。近年来,诸多学者开始尝试使用地理信息系统以及遥感数据对海平面上升的影响进行实时监测和分析[13-15]。易思[16]使用多种地理分析方法对海平面上升和风暴潮的复合作用进行风险评估。高超等[17]则深入分析了海平面上升对我国大陆沿海地区的影响。吴涛等[18]对未来50 a上海海平面上升高度进行预测,并使用地理信息系统计算该地区潜在淹没区域和范围。综上所述,相关研究的研究对象和研究方法较为单一,缺乏多种方法的结合;研究多集中在某一时间截面,缺少时间维度上的预测性研究,因此开展时空尺度上的多指标海平面上升影响预估研究就显得尤为重要。
上海大都市圈是我国的经济中心之一,其特殊的地理区位使其容易受到海平面上升的影响。在上海大都市圈蓬勃发展的趋势下,在区域一体化进程的推动下,有必要对该地区开展长时间维度的海平面上升进行预测。所用数据主要来自地理空间数据云平台、中国科学院资源环境科学数据中心、联合国政府向气候变化专门委员会以及美国地质勘探局。2050年作为我国基本实现社会主义现代化、长三角一体化和上海全面建成卓越全球城市的重要时间节点,城市发展建设的安全性和经济性至关重要。因此选取2050年为时间节点,基于遥感数据、气象数据和社会经济数据,建立上海大都市圈海平面上升影响评价指标体系,使用BP神经网络模拟、CA-Markov模拟和前移回归分析等方法对相关数据进行时间和空间尺度上的预测,并使用地理信息系统对数据进行叠加处理,得到不同等级的影响指数区划。为上述地区后续经济社会发展重点和城市建设方向的选取的合理性提供科学依据和保障,并为类似地区应对海平面上升影响应对提供科学的指导思路。
1 研究方法
1.1 海平面上升影响预估指标体系的构建
海平面上升的影响预估是对某地区未来海平面上升可能造成的影响进行分析和判断的过程[21-23]。本文深入分析海平面上升的可能影响因素和结果,构建由潜在损害性、脆弱性和抵御性三个决策层维度构成的海平面上升影响预估评价指标体系。其中潜在损害性指标,主要表征为与海平面上升较为相关的自然事件的强度,如海平面上升高度、洪涝影响等相关影响因子的强度和频度;脆弱性指标是指可能受到海平面上升影响的社会经济因素指标的分布和程度,如人口分布、房屋建筑、农作物、重大基础设施等;抵御性指标则主要表示应对海平面上升的抵御、防御和反应能力等,主要包括政府响应程度、防护设施等级和密度等。一般来说一个地区的海平面上升影响的潜在损害性指数越高,海平面上升所导致的影响强度就越大;海平面上升影响的脆弱性指数越高,表明该地区在面临海平面上升时的潜在损失越大;海平面上升影响抵御性指数越高,说明该地区防范和应对能力越强,可能造成的损失就越小。
上海大都市圈海平面上升影响指数的计算公式如下:
I=f(P+V-R),
(1)
式中:I(Impact)为海平面上升影响指数,P(Potentially damaging)为潜在损害性指数,V(Vulnerability)为脆弱性指数,R(Resilience)为抵御性指数。
同时利用加权综合评分法,构建海平面上升影响指数的评估模型,各类评价因子分级后的结果分别用于计算潜在损害性指数(P)、脆弱性指数(V)和抵御性指数(R)的结果,综合上述三个指数结果计算海平面上升影响指数。
加权综合评分法的通用模型如下:
(2)
式中:E代表各决策层指标(P、V和R)的加权得分结果,Qi为第i个因子层指标的权重,Ci为第i个因子层指标的评价得分。
由此,即可建立海平面上升影响预估评价指标体系。综合考虑指标体系的科学性、代表性和可推广性,结合上海大都市圈各地区的指标获取的难易程度,确定指标体系的具体指标,使用AHP层次分析法将指标体系分为决策层、中间层和因子层。同时使用层次分析法确定各指标之间关系和权重,在咨询相关专家的基础上,构建同级各指标间的判断矩阵,对指标间的最大特征值和特征向量进行研判,并对结果进行一致性检验,最终得到各指标的权重,见表1。
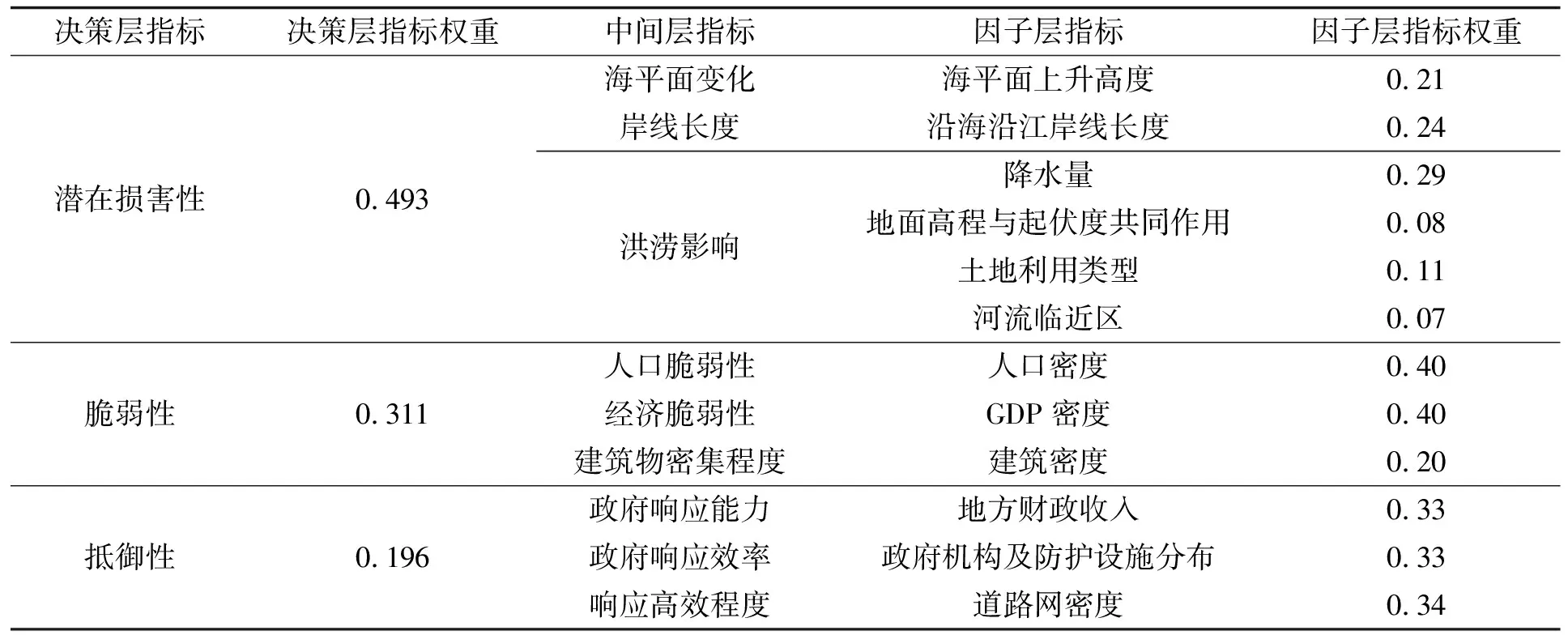
表1 上海大都市圈海平面上升影响预估指标体系及权重Tab. 1 Estimate index system and weights of the impact of sea level rise in Shanghai metropolitan area
同时根据影响指数的计算公式和加权综合评分法的通用模型,结合指标体系和权重,对各决策层指标得分的上限做出说明:除影响指数的最大值为6.08外,其余得分最大值均为10;各不同指数间的得分不具有可比性。
本文是对2050年上海大都市圈海平面上升影响的预估研究,需对海平面上升高度、降水量变化、人口密度、GDP密度、建筑密度、地方财政收入和道路网密度等指标进行模拟预测;其余沿海沿江岸线长度、地形因素等指标具有一定的稳定性和长久性,可采用现有数据表征2050年的情况。其中海平面上升高度采用IPCC (Intergorernmental Panel on Climate Change)公布数据,其余数据则采用不同方法进行模拟预测。
1.2 BP神经网络模拟法模拟降水量

图1 BP神经网络结构图Fig.1 BP neural network structure diagram
神经网络方法是一种来源于人类脑神经运作的平行分散式的数据模拟处理模型,具有自行组织、学习的能力,具有较强的容错性和良好的非线性逼近能力,在各个学科和领域具有广泛地应用,在实际运用中多用于经济规模、故障检测、降水量预测等[24-25]。而BP神经网络是一种基于误差调整方向多向传播的多反馈网络,是基于Widrow-Hoff学习算法和非线性可微转移函数的神经网络模型。其网络一般具有三层或三层以上的结构,主要为输入层、多层隐藏层和输出层,各因子之间实现全连接,各隐含节点一般使用Sigmoid激励函数进行运算,主要结构如图1所示。
BP神经网络的计算过程包括以下几个步骤:
①将学习样本输入模型,进行网络初始化,计算隐藏层的启动值,根据输入x向量,输入层与隐藏次权值ωij以及隐藏层阈值aj,计算输出值。其中i为节点数:
(3)
其中节点数的转移Sigmodi函数为:
f(x)=1/(1+ε-x)。
(4)
②根据输出层H每一集输出层阈值bk,计算预测输出O:
(5)
③随后根据预测输出H和期望输出Y计算预测误差e,并依据误差e进行判断预测值是否合理,若不合理,则需要对权值ωij和ωjk进行更新;
ek=Yk-Ok,
(6)
(7)
ωjk=ωjk+ηHjek。
(8)
④根据误差e更新网络的节点阈值a,b。由此判断算法是否完成迭代,若没有完成,则继续循环上述第3步直至完成迭代:
(9)
bk=bk+ek。
(10)
根据上述神经网络方法,结合上海大都市圈气象站点历史观测数据,预测2050年上海大都市圈雨季的日值降水量。同时使用经验公式将降水量对洪涝的影响进行转化:
(11)
式中:f(x)为降水量影响因子,输入数据x为最大连续3d降水量(mm)。
1.3 CA-Markov模拟法模拟空间因素
CA-Markov是整合了元胞自动机(cellular automata)和马尔科夫模型的土地利用类型的预测模型[26]。元胞自动机是具有时空计算特征的动力学模型,能够模拟复杂的自然和社会现象,具有时空和状态离散的特点,主要表示为:
(12)
式中:S为元胞有限、离散的状态集合;N为元胞的邻域;t,t+1表示不同的时刻;f为空间元胞的状态转化规则。Markov模型是处理栅格的空间概率模型,具有后续无效性的特点,常用于地理信息的预测。CA-Markov模型的主要原理和计算公式如下:
①马尔科夫过程:在事件发展过程中,如果状态转移过程无后效性,即每次状态转移都与且只与前一时刻的状态有关,这样的过程称为马尔科夫过程。
②状态转移矩阵:在事件发展过程中,从某一种状态转移到下一时刻其他状态的可能性,称为状态转移矩阵,记为pij。在土地利用结构的预测中,状态通常指的是土地利用类型,如建设用地、非建设用地等。
③状态转移概率矩阵:假定某一事件发展过程中有n个可能的状态,并记pij为状态Ei的状态转移概率,则下面矩阵被称为是状态转移矩阵:
(13)
④状态转移概率矩阵的计算:计算状态转移概率矩阵p,即求每个状态转移到其他任何一个状态的状态转移概率pij,其计算的基本方程为:
(14)
具有无后效性和齐次性两个特征的马尔科夫链,满足以下方程:
(15)
首先基于CA-Markov模拟法,使用2005年和2010年数据模拟2015年土地利用情况以此进行结果的精度检验,所得Kappa系数为0.83,证明该方法适用于该地区。随后以2010年和2015年的土地利用类型数据作为模型的运行起始时间,以5 a为周期,模拟2050年上海大都市圈的土地利用空间分布状况。同时使用该技术对2050年上海大都市圈的GDP密度和人口密度等空间因子进行预测。
1.4 前移回归分析法模拟社会经济因素
回归分析是建立在历史数据的基础上,选取分析对象中具有代表性的变量作为自变量和因变量,进一步探寻事物发展的内在联系,并以数学方程式的方式表现出来的方法。回归分析多用于经济发展预测、成本分解和销售预测等经济活动[27]。但回归分析法应用较为受限,只有在保证同期其余变量可知的情况下才能求得,所以本文使用前移回归分析法对上海大都市圈的地方财政收入进行预测。
前移回归分析法是基于事物发展是具有前兆和基础的原理进行的[28]。基于前一时间段的指标值是后续时间段指标值的基础的观点,将回归方程写为:
y1=b0+b1x1+b2x2+…bpxp,
y2=b0+b1x11+b2x12+…bpx1p+φ1,
⋮
yn=b0+b1xm1+b2xm2+…bpxmp+φm,
(16)
其中:m=n-1,基本运算方法与普通回归模型相同。将历史地方财政收入代入,设定循环次数,即可获得2050年上海大都市圈的区县级地方财政收入。
1.5 指标量化法
由于各指标单位和维度不同,为方便数据比较,需对指标进行量化并赋值,依据不同划分标准将各指标划分为高、较高、中、较低和低等五个等级,并分别赋予10、8、6、4、2的无量纲量化得分。其中沿海沿江岸线长度、人口密度、GDP密度、建筑物密集程度、地方财政收入、政府机构及防护设施分布和道路网密度等指标均采用百分比位序法对指数进行量化得分。其余指标的量化标准详见表2。
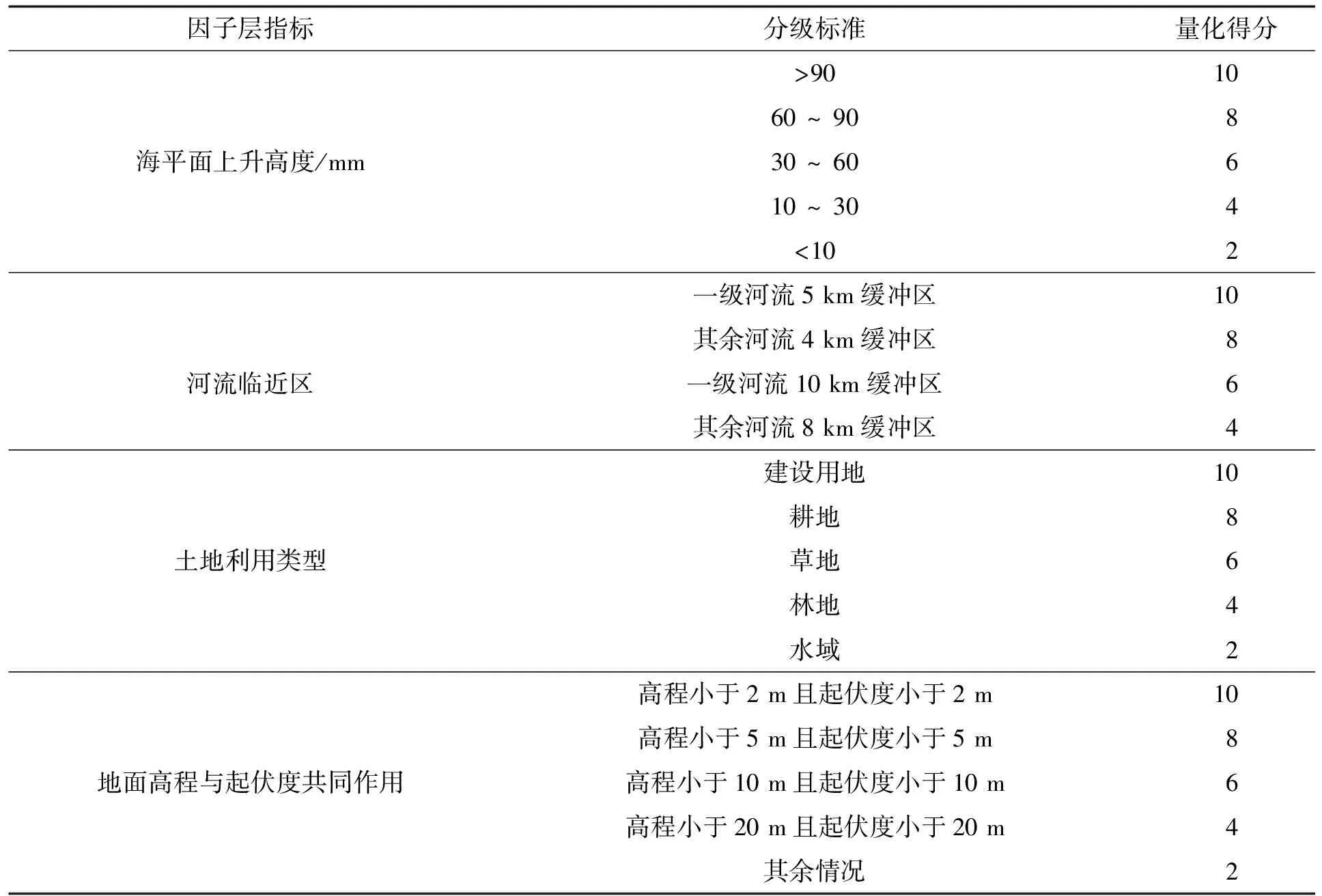
表2 部分指标分级标准和量化得分Tab.2 Quantitative standards and scores of some indicators
2 影响预估结果与等级区划
基于第二部分的数据预测方法获取到上海大都市圈2050年相关数据,并根据海平面上升影响预估评价指标体系和各指标加权综合评分法,计算得到2050年上海大都市圈海平面上升影响的潜在损害性指数、脆弱性指数、抵御性指数和影响指数。同时以市级(直辖市、地级市)、区县级行政区划为评估单元,使用分区统计技术对潜在损害性指数、脆弱性指数、抵御性指数和影响指数进行统计计算,并使用地理信息系统进行可视化展示。
2.1 潜在损害性指数评估
根据图2可得,潜在损害性指数较高的区域主要为沿海沿江以及沿湖区域,其指数最大值为9.41,最小值为1.85;空间分布呈现中部、东部高,西部、南部低的特征。同时结合图3和表3,对市级(直辖市、地级市)尺度的潜在损害性指数进行分析:舟山市和上海市所面临的海平面上升的潜在损害性最大,平均潜在损害性指数为6.33和6.28;上述地区多属于群岛以及冲积平原地区,且平均地面高程低、地势平坦、沿海沿江岸线漫长、暴雨频发、易于受到台风等风暴潮的影响,极易受到海平面上升的直接影响。苏州市、南通市、嘉兴市的洪涝影响较高、地面高程低,但其受海平面直接上升的影响较小,综合评价后其潜在损害性指数仍然偏高。至于宁波市、无锡市、常州市和湖州市,或因地面起伏度高,或因洪涝影响程度较低,或因沿海岸线较短等原因,所以其潜在损害性指数相对较低。
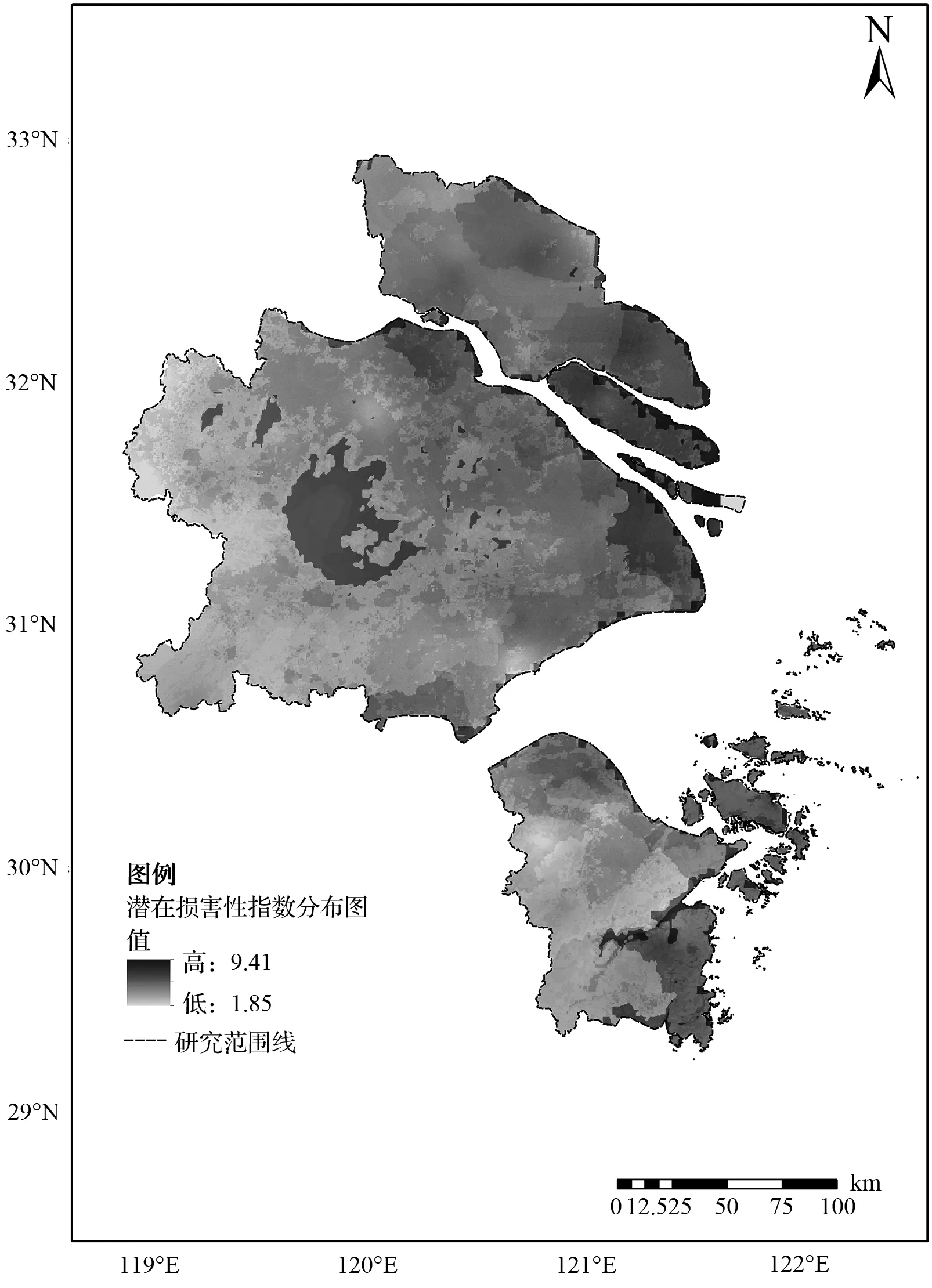
图2 潜在损害性指数分布图Fig.2 Distribution diagram of potentially damaging index
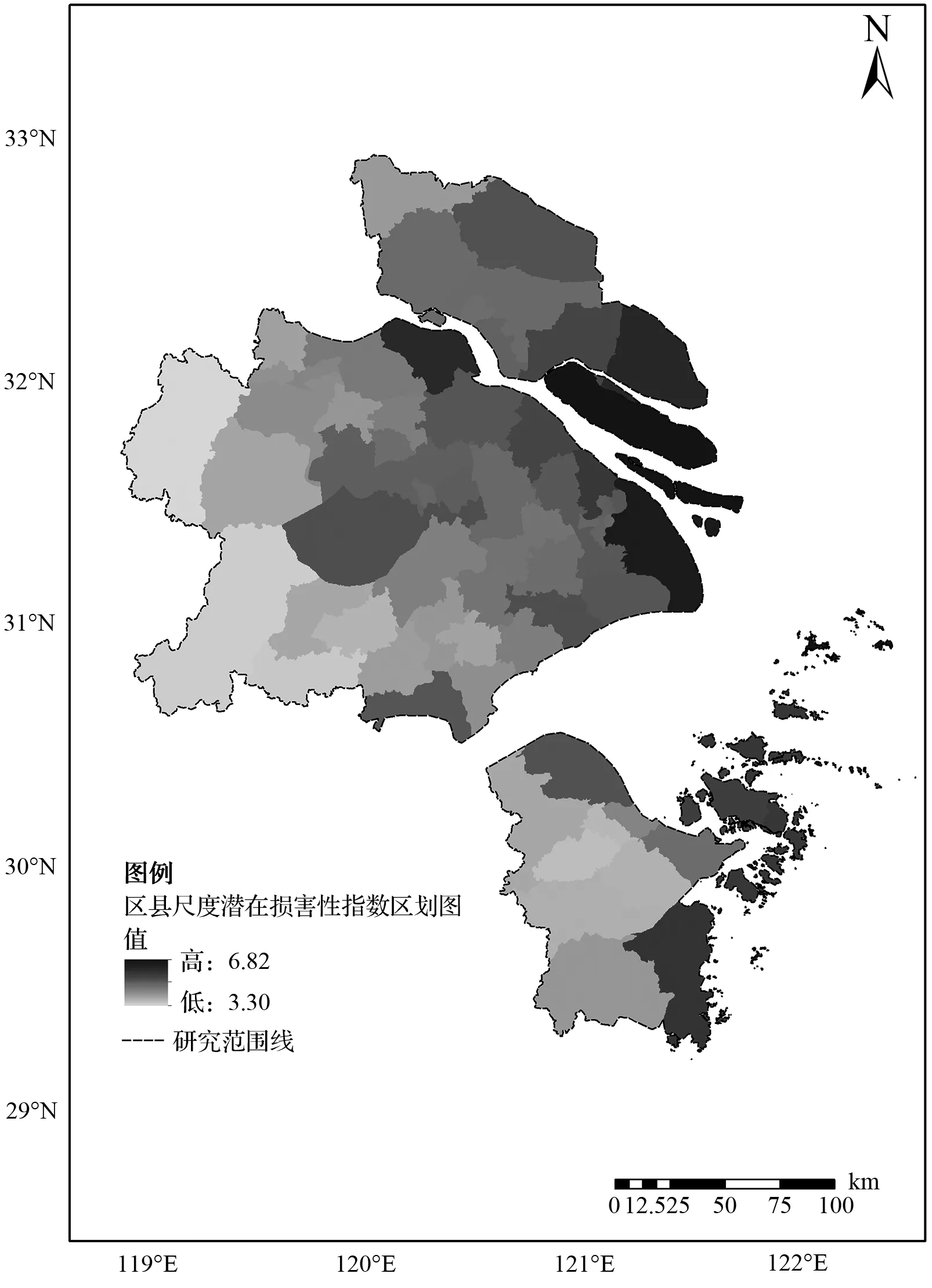
图3 区县尺度潜在损害性指数区划图Fig.3 Zoning map of county-level potentially damaging index

表3 各市(直辖市、地级市)海平面上升潜在损害性指数Tab.3 Sea level rise potentially damaging index by city (municipal municipality and prefecture-level city)
2.2 脆弱性指数评估
根据图4分析可得,脆弱性指数较高的区域主要为人口密集、地势相对平坦以及河流分布密集的东部以及中部地区,其指数最大值为10,最小值为2;呈现中部、东部高,西部、北部和南部低的特征。同时结合图5和表4,对市级(直辖市、地级市)尺度的脆弱性指数进行分析:上海市、无锡市、苏州市和嘉兴市等地区,表现为高度的GDP密度和人口密度,其暴露在海平面上升影响中的脆弱性指数较高。常州市、舟山市、宁波市等地GDP密度较高,但人口密度相对较低、建筑密集程度不高,其脆弱性指数相对较低。而南通市和湖州市经济相对不发达、人口相对较少,其脆弱性指数较低。
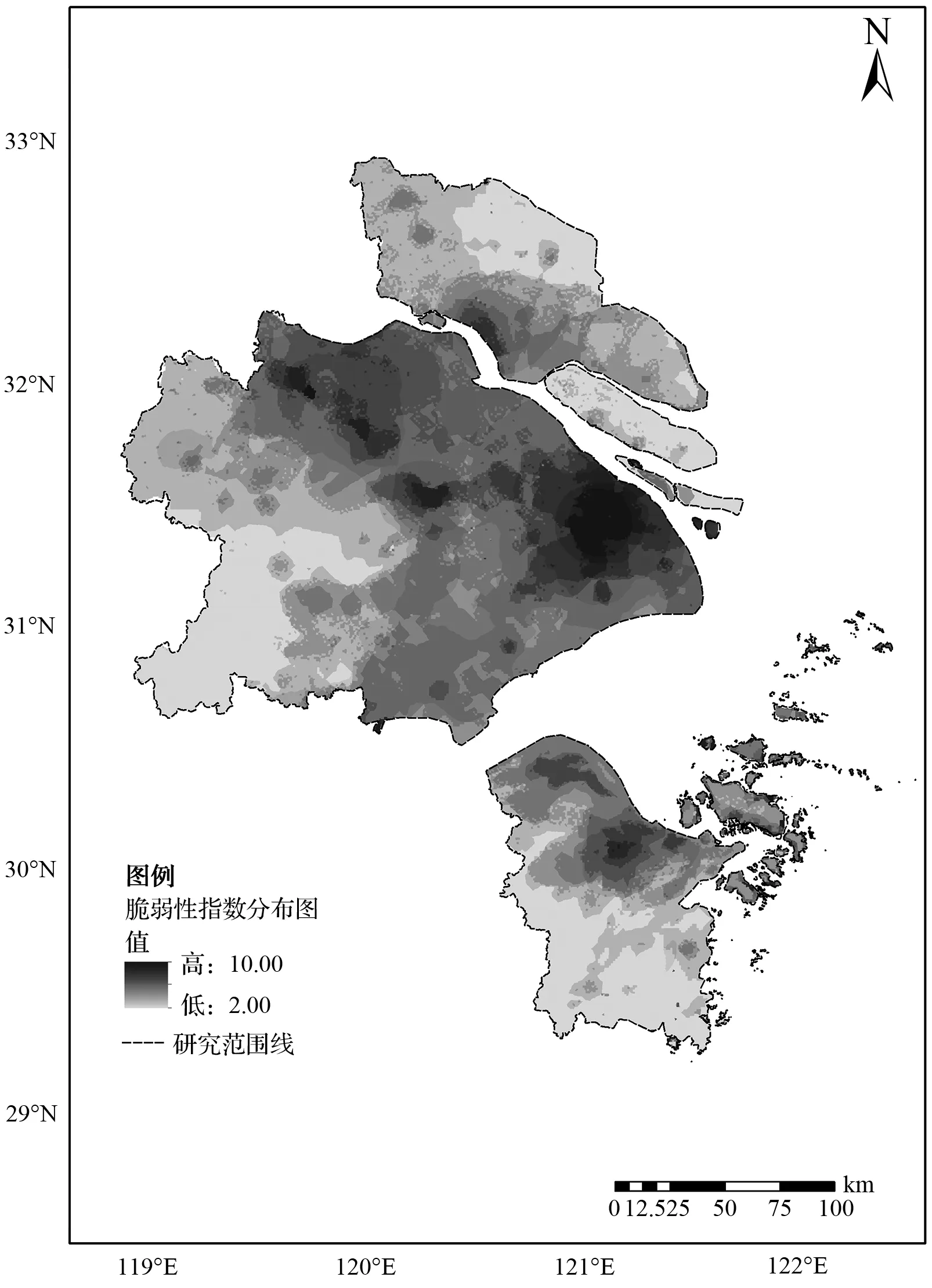
图4 脆弱性指数分布图Fig.4 Distribution diagram of vulnerability index

图5 区县尺度脆弱性指数区划图Fig.5 Zoning map of county-level vulnerability index

表4 各市(直辖市、地级市)海平面上升脆弱性指数Tab.4 Sea level rise vulnerbility index by city (municipal municipality and prefecture-level city)
2.3 抵御性指数评估
根据图6可得,抵御性指数较高的区域主要为长江南岸以及钱塘江入海口南侧,其指数最大值为10,最小值为2;空间分布呈现中部高、其余地方低的特征。同时结合图7和表5对市级(直辖市、地级市)尺度的抵御性指数进行分析:上海市、常州市、苏州市以及无锡市的地方财政收入水平高、政府服务设施及防护设施分布密集,有利于应对海平面上升所带来的影响,具有较强的应对能力;同时具有较高的道路密度,具有较强的疏散能力,因此上述地区的抵御性指数较高。宁波市、嘉兴市和南通市的财政收入水平较高,但其政府服务和防护设施分布稀疏、道路密度较低,它们的抵御性指数相对较低。湖州市和舟山市的地方财政收入、政府服务和防护设施密度和道路密度均较低,它们的抵御性指数较低。

表5 各市(直辖市、地级市)海平面上升抵御性指数Tab.5 Sea level rise resilience index by city (municipal municipality and prefecture-level city)
2.4 海平面上升影响预估及等级区划
综合上海大都市圈海平面上升影响指数的计算公式以及潜在损害性、脆弱性和抵御性的结果,得到上海大都市圈海平面上升影响指数,并使用自然间断法进行等级划分,得到不同等级的区划结果(图8、图9、表6、表7)。
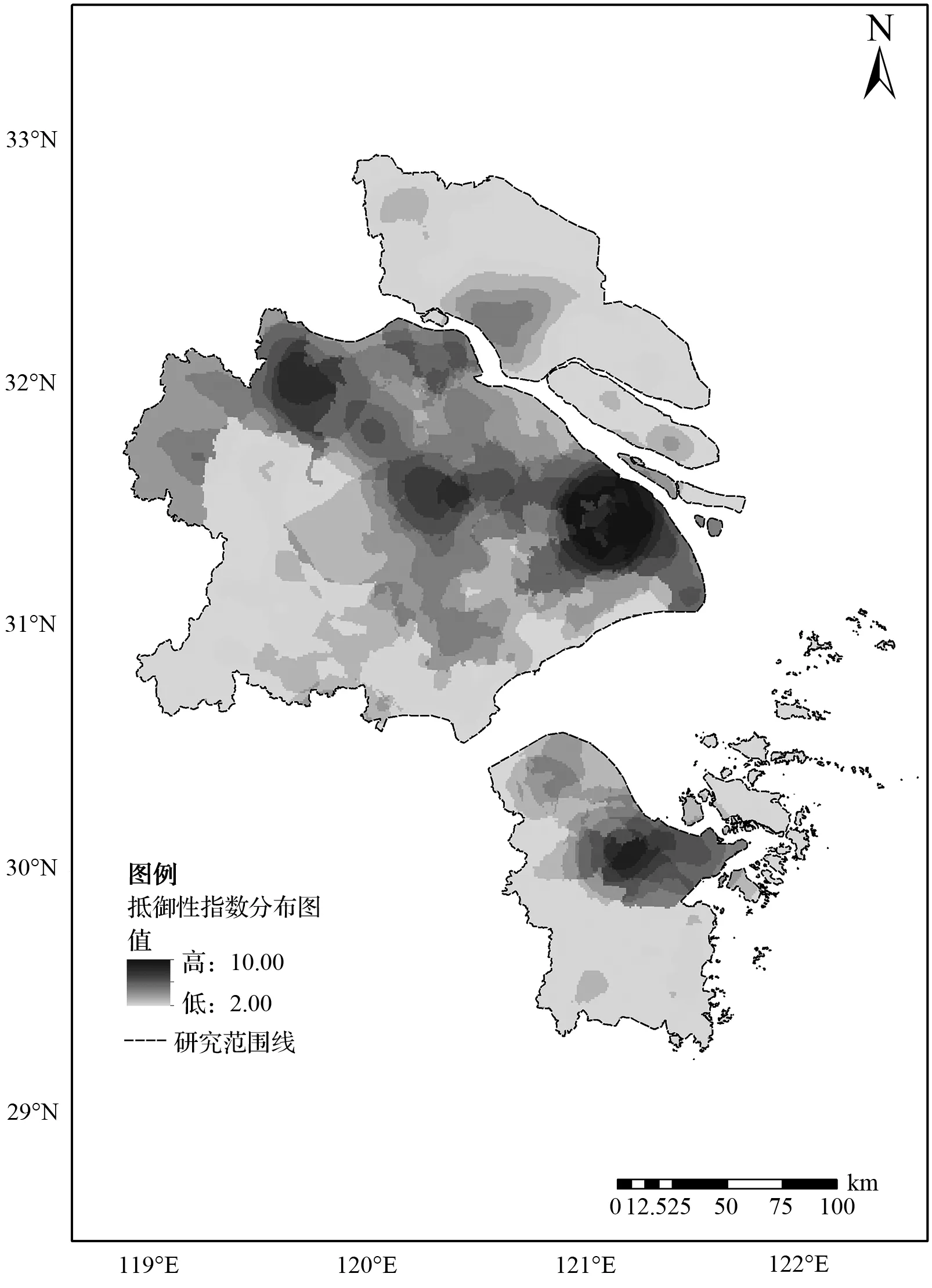
图6 抵御性指数分布图Fig.6 Distribution diagram of resilience index

图7 区县尺度抵御性指数区划图Fig.7 Zoning map of county-level resilience index
由图8和表6分析可得:2050年上海大都市圈共有约21 500 km2的用地表现为中度以上影响等级,约占该区域面积的40 %,主要为距海岸线0~10 km地区、长江南岸0~15 km地区、长江北岸0~10 km地区以及太湖沿岸等地区,该地区降水频繁、地势低洼且平坦,易受到海平面上升的直接影响。其余地区的海平面上升影响等级则主要表现为中度和低度,受海平面上升的影响较小。
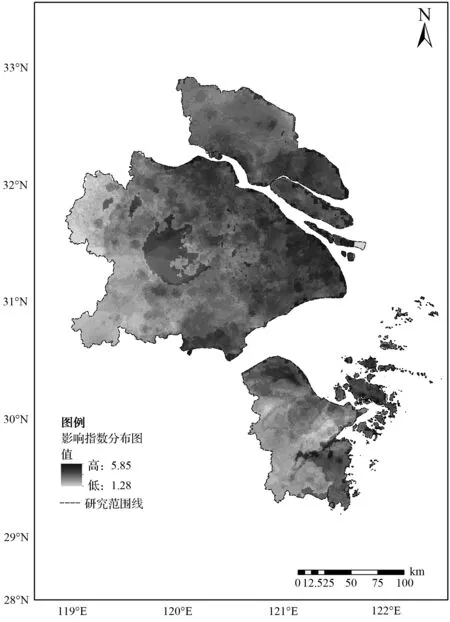
图8 影响指数分布图Fig.8 Distribution diagram of impact index
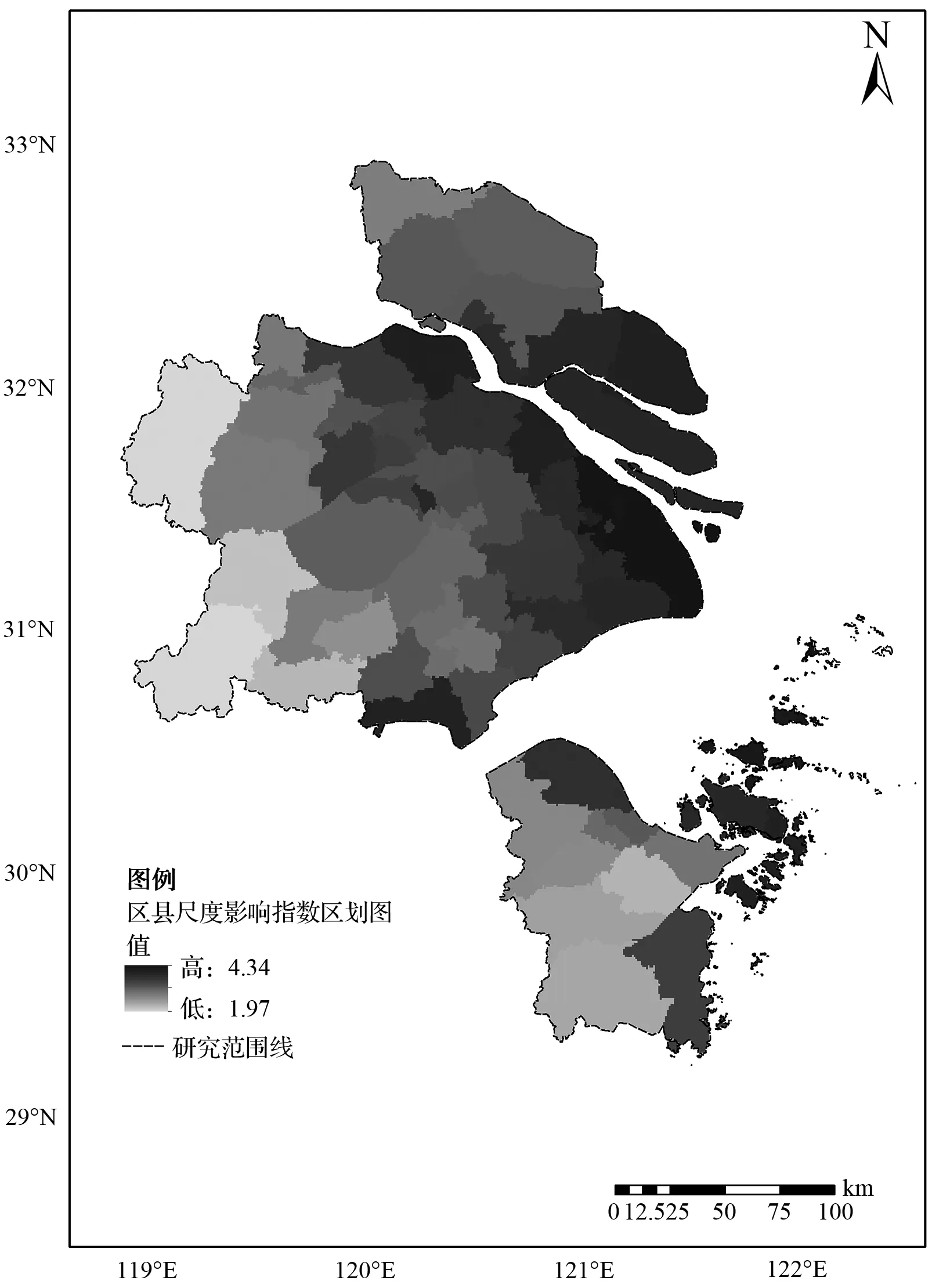
图9 区县尺度影响区划图Fig.9 Zoning map of impact index

表6 各指标等级占比划分Tab.6 Classification of various index levels

表7 各市(直辖市、地级市)海平面上升影响指数Tab.7 Sea level rise impact index by city (municipal municipality and prefecture-level city)
结合图9和表7,从行政区划角度进行分析,2050年舟山市海平面上升影响指数为4.04,主要因为该市地形多为岛屿、散布在海内,其潜在损害性指数最高且脆弱性指数位居各市(直辖市、地级市)中游,但抵御性指数却排在最后一位,综合分析其海平面上升影响指数是最高的。而其他地区或是因为潜在损害性指数较高如上海市,或是脆弱性指数较高如苏州市,或是抵御性指数较差如南通市、嘉兴市,导致它们面临的海平面上升影响较高。但无锡市、宁波市等地因为其潜在损害性指数较低,且具有相对较高的抵御性能力从而抵消了一部分潜在损害性因素的影响,程度有所下降。常州市和湖州市则因为其潜在损害性和脆弱性指数不高,且具有较强的抵御性能力,所以其海平面上升影响最低。
从影响预防和管理视角出发,对不同的影响等级区域采取不同的应对和处置措施。对于高度影响的舟山市、上海市等地,政府和社会各界需要提高防范和危机意识,在海岸带地区开发建设时应充分评估海平面上升的影响,加大对沿海堤防等硬件设施的投入;对于中度影响的苏州市、南通市和嘉兴市则应根据当地实际情况对海平面上升影响预防和发展建设进行充分评估;对于低度影响的无锡市、宁波市、常州市和湖州市,可能需要提高必要的应对等级。
3 结语
选取上海大都市圈作为研究范围,以2050年为时间节点,构建由潜在损害性、脆弱性和抵御性等三个决策层维度、海平面上升淹没、人口密度和道路密度等12个指标的海平面上升影响预估评价指标体系,展开对海平面上升影响的预估。
①使用BP神经网络模拟法、CA-Markov模拟法和前移回归分析法等多种方法对2050年上海大都市圈相关数据进行科学预测,多种科学的模拟预测方法为海平面上升背景下的影响预测奠定了基础。
②基于海平面上升影响预估评价指标体系和计算公式,得到海平面上升影响程度及其空间分布:2050年上海大都市圈共有约21 500 km2的用地表现为中度以上影响等级,约占该区域面积的40 %,主要为距海岸线0~10 km地区、长江南岸0~15 km地区、长江北岸0~10 km地区以及太湖沿岸等地区。以行政区划为单元进行分析可得,舟山市、上海市的海平面上升影响较大,易受到较为严重的海平面上升影响;苏州市、南通市和嘉兴市则表现为中度影响;无锡市、宁波市、常州市和湖州市表现为低度影响。
③影响预估的准确性受制于评价方法的科学性和指标体系的全面性。受限于资料的可获取性,本文仅选取了12个指标,主要考虑了空间因素和经济指标的影响,缺乏对社会指标的考虑。指标体系的构建和指标的模拟预测方法有待进一步改善。

