导函数的零点不可求怎么办？

◎张运能

在导数大题的求解或证明中，很多时候需要求解函数或者导函数的零点，学生对于处理函数零点可求时可能较为熟练，但在面对函数的零点不可求或零点不存在情形等问题时，就手足无措，无从下手了。我们是否就是"束手无策"呢？显然不是！对于这一类问题的求解，可从以下三方面入手解决。

一、猜根：通过观察方程的结构特征，猜出方程f′（x）＝0 的根

对于有关x 与ln x 的组合函数为背景的试题，要求学生理解导数公式和导数的运算法则等基础知识，准确的求出函数的导数，当所求的导函数解析式中出现lnx时，常猜x＝1；当函数解析式中出现ex时，常猜x＝0，然后代入未知数x 的值进行检验，看看满足方程f′（x）＝0 吗？

（1）若函数f（x）在（a，a＋1）上有极值，求实数a 的取值范围；

（2）若关于x 的方程f（x）＝x2－2x＋k有实数解，求实数k 的取值范围．

（2）由已知可得，方程f（x）＝x2－2x＋k 有实数根，

即f（x）－x2＋2x＝k 有实数根．

设g（x）＝f（x）－x2＋2x，

接下来，需求函数g（x）的单调区间，所以需解不等式g′（x）≥0 及g′（x）≤0，因而需解方程g′（x）＝0。但此方程不易求解，所以我们可以先猜后解．

因为g′（1）＝0，且当0＜x＜1 时，g′（x）＞0，当x＞1 时，g′（x）＜0，所以函数g（x）在（0，1）上单调递增，在（1，＋∞）上单调递减

所以g（x）max＝g（1）＝3/2。当x→0时，g（x）→－∞；当x→＋∞时，g（x）→－∞，所以函数g（x）的值域是（－∞，3/2），所以所求实数k 的取值范围是（－∞，3/2）。

对于这种猜想方程的根的方法，有时可以减少很多解方程的运算过程，从而提高解题速度，但学生往往不太敢用或者不习惯用，在教学中需要老师主动引导，积极培养。

二、设根：通过运算代换、数值估计，虚设f′（x）＝0 的根

有这么一类试题，导函数的零点无法求解，但我们能判断零点是存在的，我们可以把这一类问题形象地称作“隐零点问题”。这个零点就是我们所说的“隐零点”，它是客观存在的，但是又不那么好找，对于这一类问题的求解，往往可以采用“虚设零点、整体代换”的方法，虽然不能求解导函数的零点，但我们可以假设零点是x0，这种方法称为“虚设零点法”，于是就有f′（x0）＝0。而在进一步的问题求解中，我们经常会遇见一些较为复杂的函数式，例如指数式与对数式、幂函数式等的混合，这时我们可以利用f′（x0）＝0 来代换，将超越式（指数式、对数式等）替换成简单易于求解的函数式，进而求解相关问题。

例题2．已知函数f（x）＝aex－bln x，曲线y＝f（x）在点（1，f（1））处的切线方程为

（1）求a，b；

（2）证明：f（x）>0。

解：（1）函数f（x）的定义域为（0，＋∞）．

所以f′（x）＝0 在（0，＋∞）上有唯一实根x0，且x0∈（1，2）．

当x∈（0，x0）时，f′（x）<0，当x∈（x0，＋∞）时，f′（x）>0，

从而当x＝x0时，f（x）取极小值，也是最小值．

则x0－2＝－ln x0

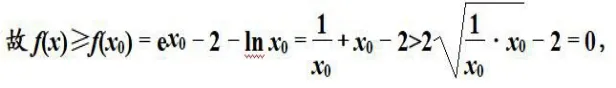
所以f（x）>0。

诸如此类的例题有很多，同学们要学会应用。“虚设零点法”常用到的解题技巧主要可以归纳为以下几点：（1）整体代换，将超越式转化为普通式。利用这类技巧，可以通过逐步分析零点所在区间以及满足的关系讨论函数的单调性，最后利用零点所满足的恒等关系整体代入，将函数关系转化为普通式。（2）反代消参，构造关于零点的单一函数。如果问题要求解的结论与参数无关，这时一般不要用参数来表示零点，而是反过来用零点表示参数，然后把极值函数变成关于零点的单一函数再进行求解。（3）降次留参，建立含参数的方程或不等式。如果问题要求解的结论与参数有关，可利用导数为零的方程，在保留参数的情况下，不断把零点的次数降到不可降为止，再结合其他条件，建立含参数的方程或不等式，就可求出参数的值或者取值范围。

三、证无根：通过讨论函数的单调性，证明方程f′（x）＝0 无根

有些函数的一阶导数f′（x）是无零点的，即f′（x）＝0 无解，当利用导函数求函数f（x）在区间[a，b]，[a，b）或（a，b]上的最值时，可首先考虑函数f（x）在该区间上是否具有单调性，若具有单调性，则f（x）在区间的端点处取得最值（此时若求f′（x）＝0的根，则此方程是无解的）．

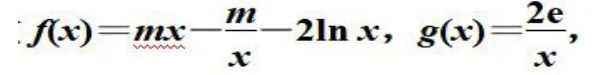
例题3.已知m∈R，函数若Ex0∈[1，e]，使得f（x0）＞g（x0）成立，求实数m 的取值范围

分析：因为当x＝1 时，f（x）＝0，g（x）＝2e，不存在f（x0）＞g（x0），所以关于x 的不等式f（x）＞g（x）在[1，e]上有解，即关于x的不等式

可大胆猜测方程u′（x）＝0 无解，证明如下：

所以u′（x）＜0，u（x）在（1，e]上是减函数，

求函数零点问题，是高考试卷中的热点问题，这类问题常以基本初等函数或分段函数为载体，考查函数零点的存在区间、确定零点的个数、参数的取值范围、方程的根或函数图象的交点等问题。不仅考查考生计算、画图等方面的能力，还考查考生函数与方程、数形结合及转化化归等数学思想的综合应用。在解决函数零点问题时，除了应用上面介绍的三种办法外，既要注意利用函数的图象，也要注意根据函数的零点存在性定理、函数的性质等进行相关的计算，把数与形紧密结合起来。所以学生在平时的训练中要有意识的加以培养和应用。