一种移动边缘计算下基于高斯隐藏贝叶斯的服务质量监控方法

张雅玲，张鹏程，金惠颖

(河海大学 计算机与信息学院，南京211100)E-mail：2460154274@qq.com

1 引 言

移动边缘计算是一项新兴技术，通过在移动客户端和服务器之间部署靠近移动端的边缘服务器提供服务，因此具有响应时间短、处理速度快等特点[1].随着这些新技术的不断发展，Web服务也逐渐运用于人们生活的各个领域，包括商业、工业、医药及娱乐等领域[2].部署在互联网上的Web服务的数量在快速的增长，并且逐步转移到移动边缘端，其中不同的服务提供商可能会提供功能相似的服务，相同的服务在不同的边缘服务器上表现的效果也大有不同.如何选择满足用户需要的服务，成为人们关注的焦点问题[3]，由此引入了QoS(Quality of Service)的概念，QoS表示服务的非功能属性，主要包括响应时间、吞吐量、可靠性及可用性等[4].

具有QoS保证的移动边缘服务是人们选择服务的主要关注点，通常服务的QoS数据是由服务提供商提供，某些提供商可能会提供虚假信息以吸引用户，其不足以评价服务的好坏.因此，为了保证服务的正常运行，有效地监控服务的QoS显得尤为重要[5-7].

监控技术是检验服务是否失效的最有效的方法[8].一般来说，QoS属性标准可以用概率质量属性的方式来表达[9]，如响应时间可描述为“某服务对客户请求的响应时间小于1s的概率为80%”.基于这种概率质量属性标准，研究人员在传统网络环境下提出了许多QoS监控方法.然而现有的这些方法在移动边缘环境下存在一定的问题，分析如下：

1)用户的移动性使得传统监控决策方法在边缘环境下不可用.在移动边缘环境下，用户位置的不断变化带来边缘服务器的切换，因此在监控过程中，当用户移动到新的边缘服务器时，旧边缘服务器上的历史数据就会失效[10]，传统的方法仅通过旧服务器上的历史数据进行决策致使监控结果不再准确.某用户a早晨基于家附近的某个边缘服务器调用服务，监控结果显示服务运行正常.当其地理位置切换到学校时，便会调用新的边缘服务器，传统的监控方法仍会利用旧边缘服务器上的历史数据对服务进行监控并且监控结果显示成功，然而由于该用户位置的改变此时的服务状态早已失效.

2)QoS属性值之间的依赖性致使监控结果发生偏差.在移动边缘环境下，同一个边缘服务器中的QoS值之间有很大的依赖性，现有基于朴素贝叶斯分类的监控方法中假设属性值之间相互独立忽略了属性值之间的影响，从而将导致服务监控的滞后判断.同样的，该用户切换到学校附近的边缘服务器时，传统的监控方法假设监控样本与当前服务器的失效样本相互独立，使得判断服务失效的概率降低，导致服务监控未能及时识别服务的失效.

为解决以上问题，本文提出了一种基于贝叶斯分类的移动边缘环境下的QoS监控方法.通过构造父属性来减少属性值之间的依赖性，在训练阶段为每个边缘服务器构造对应的高斯隐藏贝叶斯分类器，在监控过程中，基于用户的移动性考虑了以下三种情况：1)用户没有调用新的边缘服务器；基于当前边缘服务器的历史数据构造的贝叶斯分类器进行监控.2)用户移动到一个新的边缘服务器中，并且此边缘服务器上有历史数据构造的分类器；利用新的边缘服务器上的分类器进行监控.3)用户移动到一个没有历史数据的边缘服务器中；采用KNN算法选择邻近的边缘服务器得到监控结果.最后基于真实数据集和模拟数据集的实验对本文提出的方法进行了验证.

本文第2节对近年来相关QoS监控方法进行总结，并引出这些方法在移动边缘环境下存在的问题.第3节对本文方法中用到的相关知识进行介绍.第4节对本文提出的方法进行了详细的描述.第5节针对提出的方法在真实数据集上和模拟数据集上进行了验证.第6节对本文工作加以总结和展望.

2 相关工作

近年来，概率验证技术逐渐兴起，Chan[11]等首次提出概率监控方法，使用PCTL语言定义非功能属性的概率质量标准，计算成功样本数与总的监控样本数的比值，与事先定义好的概率标准进行比较，满足预定的标准则认为服务正常运行，否则认为服务发生违规行为.但此方法并未运用统计学进行分析和验证，因此会产生较大误差.

Sammapun[12]等通过计算成功的样本数占总的样本数量的概率，再在给定的置信水平下使用假设检验判断系统是否满足概率质量属性标准.Grunske[13]等提出了一种基于验收取样和连续假设检验的概率监控方法ProMo，方法扩展了现有的统计模型检验技术，定义了监控时的概率逻辑CSLmon，其是CSL(continuous stochastic logic)的子集，在显著性水平α和1-β下使用SPRT[14](Sequential Probabilistic Ratio Test)展示了CSLmon公式的正确性.Grunske[15]等改进了SPRT方法，通过回退统计分析并复用以前的假设检验结果实现了连续监控，减少了运行时间开销，但是当系统的实际概率在中立区时，限制其所需的最大样本数量，方法几乎失效.

贝叶斯思想的特点是将历史经验数据加入现有的预测判断，即将先验概率和似然概率相结合来表示所有形式的不确定性.Zhu[16]等提出了一种基于贝叶斯的概率属性监控方法BaProMon，方法检查运行时信息来判定监控结果是支持原假设还是备择假设，其监控结果遵循伯努利假设.为了避免贝叶斯因子落入中立区，重用了以前的监控结果，增加了差异并保持模型等价，实现了连续监控.合适的的先验分布对方法的有效性影响较大，但很难选择合适的先验分布.

Zhang[17]等提出了一种加权朴素贝叶斯概率监控方法wBSRM，方法考虑了环境因素的影响，使得监控更加贴合实际.采用TF-IDF算法来量化环境因素对监控的影响，将此量化值作为环境因子权值对每个样本进行加权.Zhang[18]等，利用滑动窗口机制及时摈弃早期冗余的样本，结合了信息增益理论动态更新权值，从而对加权朴素贝叶斯进行改进.然而在移动边缘环境下，由于用户的移动性和QoS属性值之间的依赖性，传统的监控方法可能不再适用.为了解决这些问题，本文提出了一种移动边缘环境下基于高斯隐藏贝叶斯的QoS监控方法.

3 预备知识

3.1 朴素贝叶斯分类器

贝叶斯定理的定义为：已知事件A发生的情况下事件B发生的概率，求得在事件B发生的条件下，事件A发生的概率，其用公式可表达为：

(1)

贝叶斯分类器基于贝叶斯定理并与先验概率、类条件密度相结合，由于其计算高效，算法简单而被广泛应用于数据挖掘中的分类问题中，其思想基础为：对于指定的待分类项，求解出该分类项发生的情况下各个类别发生的概率，其中最大概率的类别被认为此分类项的类别[19].令C={c0，c1，…，cj}是预定义的类别集，X={x1，x2，…，xn}是样本向量，根据贝叶斯公式：

(2)

假定当X属于类cj时，X中的元素xk和xl的取值是相互独立的，同时P(X)对于所有的分类都是一样的，所以贝叶斯分类器公式可以简化为：

(3)

3.2 KNN

k近邻法(k-nearest neighbor，KNN)是一种基本分类与回归方法[20]，其基本做法是：给定测试实例，基于某种距离度量找出训练集中与其最靠近的k个实例点，然后基于这k个最近邻的信息来进行预测.

通常，在分类任务中可使用“投票法”，即选择这k个实例中出现最多的标记类别作为预测结果；在回归任务中可使用“平均法”，即将这k个实例的实值输出标记的平均值作为预测结果；还可基于距离远近进行加权平均或加权投票，距离越近的实例权重越大.

4 移动边缘计算下基于高斯隐藏贝叶斯的QoS监控

4.1 高斯隐藏贝叶斯运行时监控(ghBSRM)

朴素贝叶斯分类模型中假设属性之间相互独立忽略了属性值之间的依赖性[21]，改进朴素贝叶斯分类器的其中一种方法是，削弱属性间的独立性，为每个属性创建一个隐藏的父属性，其代表来自其他属性的影响.改进的贝叶斯分类器结构如图1所示，π(xi)表示xi的隐藏父属性，公式可表示如下：

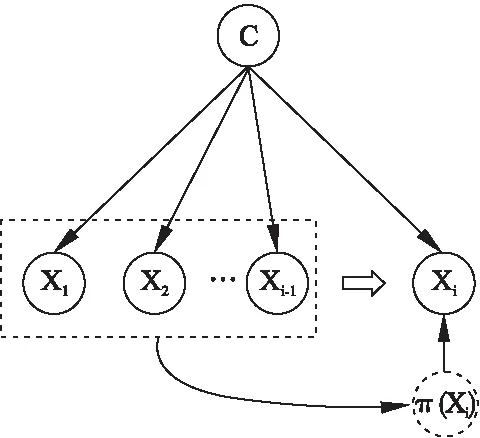
图1 改进的贝叶斯分类器结构图

(4)

贝叶斯分类器应用于连续属性的分类项时，通常假设连续变量服从某种概率分布，然后使用训练数据估计分布的参数，高斯分布通常被用来表示连续属性的类条件概率分布.在高斯分布假设下[22]：

(5)

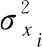
在QoS监控中，X={x1，x2，…，xn}表示一组QoS样本属性向量，令C={c0，c1}是预定义的类别集，定义样本满足概率属性标准为c0类，不满足概率属性标准为c1类.通过构造高斯隐藏贝叶斯分类器计算两类后验概率，将后验概率较大的类别作为监控的结果.

4.2 移动边缘计算下的QoS监控

由于数据的爆炸式增长，基于传统云计算模型的单一计算资源已不能满足大数据处理的实时性、安全性和低能耗等需求，由此引出了边缘计算模型[23]，其通过在移动客户端和服务器之间部署靠近移动端的边缘服务器提供服务，如图2所示，在这样一个移动边缘计算系统中，假设有一组边缘服务器集合，用户在这样的系统中活动，通过附近的边缘服务器提供服务.对用户所调用的服务的QoS进行监控时，必须要考虑到活动用户当前的边缘服务器.本文提出的移动边缘环境下的QoS监控方法的主要框架如图3所示.主要包括了三个步骤：

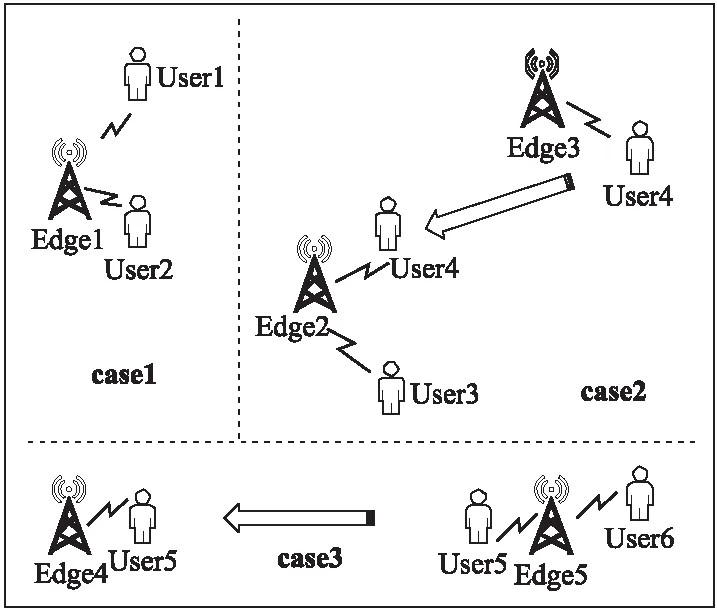
图2 移动边缘监控案例图

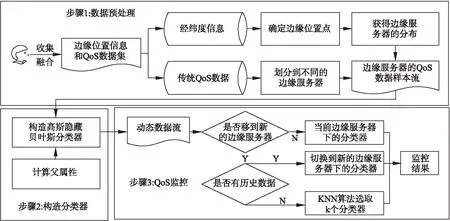
图3 QoS监控总体结构图

1)数据预处理.首先根据服务的经纬度信息进行划分得到边缘位置点，从而确定边缘服务器的分布，然后将收集到的传统环境下的QoS数据划分到各个边缘服务器中，从而构建一个边缘环境并且得到边缘服务器对应的样本数据流.

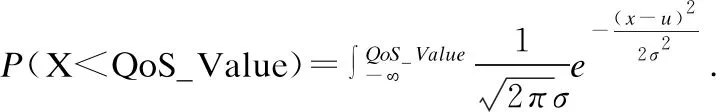
3)监控阶段.考虑用户的移动性，基于引言部分提出的三种情况进行计算：

Case 1.用户在调用服务的过程中位置没有发生变化，如图2中的用户1，2等.此时监控结果由当前边缘服务器(Edge1)的分类器得出.

Case 2.用户位置发生变化，用户从一个边缘服务器切换到另一个边缘服务器，且新的边缘服务器有历史QoS数据，如图2中的用户4，利用新的边缘服务器的监控模型进行监控.

Case 3.用户位置发生变化，用户从一个边缘服务器切换到另一个边缘服务器，且新的边缘服务器没有历史QoS数据，如图2中的用户5.采用KNN算法，找到距离这个边缘服务器最近的k个边缘服务器，记他们与这个边缘服务器的距离为：d={d1，d2，…，dk}，当前监控样本在这k个边缘服务器中的监控模型的后验概率比为：pro={p1，p2，…，pk}.根据位置进行加权，距离越近则权重越大，计算得到此边缘服务器的后验概率比值为afterpro=w1*p2+w2*p2+…+wk*pk，其中wk=x/dk，w1+w2+…+wk=1，.从而根据后验概率比值得到监控结果.

5 实 验

本节通过实验来模拟边缘监控环境并对本文提出的移动边缘计算下的QoS监控方法的合理性和有效性进行了验证，实验旨在：1)将本文提出的ghBSRM与其他监控方法进行比较；2)验证提出的方法的合理性.

5.1 实验环境配置

实验基于Geany开发平台，使用python编程语言设计并实现提出的方法，本文采用融合数据集的方法构建边缘环境并结合模拟数据集对提出的方法进行验证.数据集1(1)http：//wsdream.github.io/dataset/wsdream_dataset1.html采用的是上海电信数据集[10，24]，该数据集包括了3233个基站的位置信息以及用户调用服务的情况，本文将选取其中的一些基站来模拟一个移动边缘监控环境.数据集2(2)http：//sguangwang.com/TelecomDataset.html采用香港中文大学发布的真实世界Web服务质量数据集，该数据集包括339个用户和5825个真实世界的服务提供了响应时间的量化数据，数据含有服务位置.数据集3是按照一定约束随机生成的数据集，该数据集采用注入错误的方式对ghBSRM进行有效性检测.

对数据进行预处理，包括过滤数据和数据集的融合.过滤数据即过滤掉数据集中无效的数据，如响应时间为-1的数据.移动边缘环境下的监控过程必须要考虑边缘服务器的位置以及用户移动过程中调用边缘服务器的情况，现有的传统数据集不符合边缘要求，通过数据集融合[25]的方式获取满足边缘特性的数据集.根据服务的地理位置对真实QoS数据集进行划分，将同一位置的服务看作是一个边缘服务器中，得到60组对应边缘服务器的响应时间样本流.本文在上海电信数据集中选取了60个基站的位置与之对应，从而构建了一个边缘监控环境.图4显示的是部分基站的分布情况.

图4 边缘服务器分布图

5.2 实验结果与分析

5.2.1 ghBSRM和其他监控方法的结果比较

为了验证本文提出的方法的有效性，第一组实验采用模拟数据集测试本文的模型ghBSRM和现有的最新的几种基于贝叶斯思想的概率监控方法IgS-wBSRM、wBSRM和基于传统贝叶斯的iBSRM在相同QoS属性标准、相同边缘服务器下的监控结果.

选取edge ID为1的边缘服务器，QoS需求描述为“响应时间小于3.6s的概率大于85%”.提取真实数据集中的前2000个数据进行训练，在3000个监控样本中，在1～500，1000～2000个样本处注入响应时间大于3.6s的错误样本数大于15%，监控结果如图5所示，当样本数为106时，ghBSRM第一次监控出了服务失效，随后监控出失效的是IgS-wBSRM，而在这一阶段wBSRM并未监控出服务的异常，其并未考虑到其他样本对当前监控样本的影响导致产生的滞后判断现象.在764样本处IgS-wBSRM首先检测到了服务迁回正常状态，由于其并未考虑到前面错误样本对当前监控结果的影响，导致提前迁回的现象，可以看出ghBSRM总体上与预期结果一致.

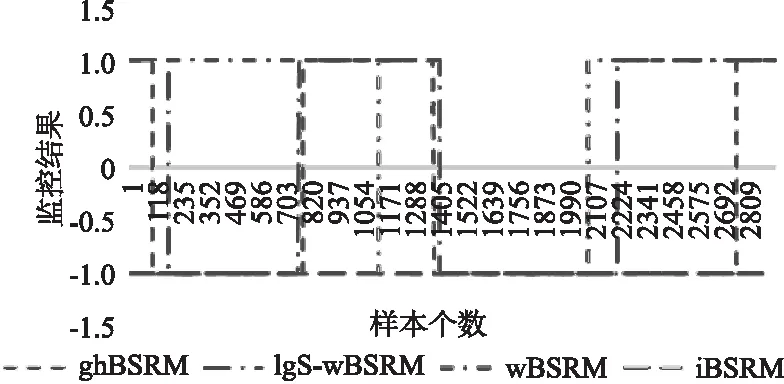
图5 不同监控方法的比较

对于这些方法的效率分析，记录了对不同QoS需求标准下的各监控方法在完成3000个监控样本所需的平均时间.本实验在本章第一部分所描述的环境下运行，具体情况如图6所示.整体上ghBSRM监控方法在运行时平均监控时间与wBSRM接近，分析可能是因为在训练过程计算参数时需要多次执行积分计算，所以平均时间与wBSRM相比没有多少提高，但是整体上优于IgS-wBSRM.

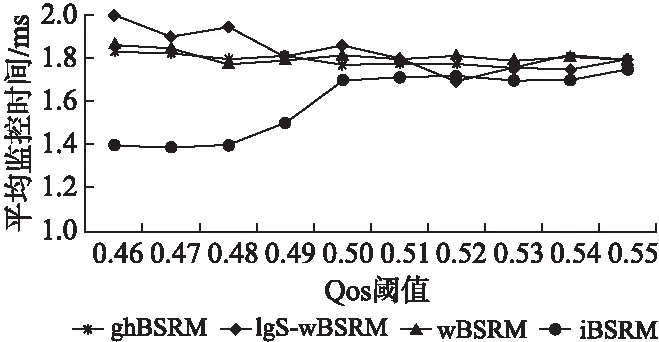
图6 平均监控时间

5.2.2 与传统环境的对比

本节将提出的ghBSRM监控方法分别在传统环境和移动边缘环境进行了对比实验，融合上海电信数据集和真实数据集，表1和表2显示用户51和62在移动过程中调用边缘服务器的情况.

表1 用户51调用边缘服务器情况

表2 用户62调用边缘服务器情况

图7表示了在QoS需求描述为“响应时间小于3.6s的概率大于85%”时这两个用户分别在传统环境和移动边缘环境下的监控结果.在移动边缘环境下，用户62在样本数为1213时开始监控出服务的失效，可以猜测这是由于该用户在移动过程中切换服务器导致了监控结果的改变，然而在传统环境下，监控结果一直保持成功状态，同样的，用户51在两种环境下的监控结果也出现了差异.实验结果表明了在移动边缘环境下，用户移动性带来边缘服务器的切换可能会导致历史数据的失效从而使得监控结果的偏差，有效证明了本文提出的移动边缘环境下的监控方法的合理性.

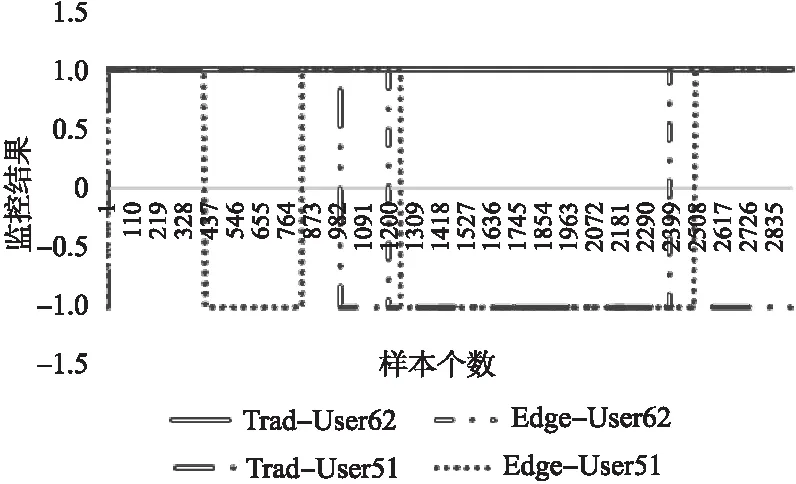
图7 监控结果

5.2.3 k值的影响

第三组实验针对本文方法中的Case3进行了验证，当用户移动到一个没有历史数据的边缘服务器中，利用KNN算法选取周边的边缘服务器进行监控.这组实验仍然采用模拟数据集进行实验，QoS需求描述为“响应时间小于3.6s的概率大于85%”，同样的，在样本数1～500，1000～2000注入响应时间大于3.6s的错误样本数大于15%.

图8显示的是边缘服务器15在没有历史数据时，分别选取周边最近的1～7个边缘服务器进行监控的结果.在第一阶段，几个不同的k值下都监控出了服务的失效.然而在第二阶段，k=5时最快检测出服务的失效情况，k=7，6，1时依次检测出错误，而k=2，3，4时未检测出异常.实验表明了在边缘服务器没有历史数据的情况下，选取的k值的不同对监控结果是有影响的，对边缘服务器15而言，选取周边5个边缘服务器进行监控是最有效的.

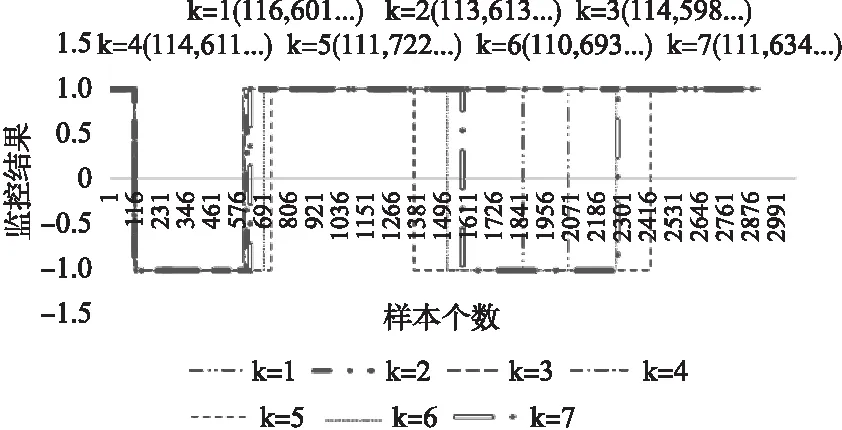
图8 不同的k值

6 总结和展望

传统的监控方法没有考虑用户的移动性和数据的依赖性，导致了监控结果的偏差.本文提出了一种基于高斯隐藏贝叶斯分类的移动边缘环境下的QoS监控方法.在真实数据集和模拟数据集上分别做了相关实验，实验结果表明了本文提出的方法的合理性和有效性.本文首先对数据集进行融合，模拟了一个边缘监控环境，通过计算父属性的值来削弱属性值之间的依赖性，为每个边缘服务器构造对应的高斯隐藏贝叶斯分类器，在监控过程中，考虑用户的移动性动态切换分类器，且在没有历史数据的情况下结合KNN算法实现移动边缘计算下的QoS监控方法.

在未来的工作中，将考虑以下几个问题：1)在没有历史数据的情况下，每个边缘服务器是否都存在一个最佳的k值，将进一步通过实验来分析和验证；2)考虑进一步将这种方法应用到多元监控中.