一种范围性空间众包任务的在线分配优化研究

高丽萍，戴 焜，高 丽

1(上海理工大学 光电信息与计算机工程学院，上海 200093)

2(复旦大学 上海数据科学重点实验室，上海 200093)

3(上海理工大学 图书馆，上海 200093)E-mail：lipinggao@usst.edu.cn；2012701442@qq.com

1 引 言

近年来随着人工智能领域的蓬勃发展，人们对于数据的需求日益增长，众包技术在数据采集中的重要地位得到了广泛的认可.空间众包技术是众包技术的一个重要分支[1，2]，空间众包严格规定了参与者的完成任务的工作地点，将采集到的数据赋予了地域性更加符合实际情况[3]，例如滴滴打车客户在指定某个地点叫车，在滴滴平台上的司机看到任务后必须要到客户所在地才可以完成任务.随着移动众包感知技术(Mobile Crowdsourcing Sensing，MCS)的蓬勃发展，信息获取手段的提升促进了在过去几年里，越来越多的国内外的学者开始对于空间众包的分配问题进行研究，并且取得了巨大的成果[4-6].

空间众包问题中主要有三个方面的研究内容：任务分配、任务规划和隐私保护.其中任务分配是保证众包任务完成的核心技术.任务分配指如何分配任务给工人来实现最大的任务分配数量和最小化任务成本，例如TGOA[2]算法将分配过程分成两个阶段，利用当前分配和当前的全局最优解作对比来考虑是否会采用，期望通过每次分配局部最优来接近全局最优.在分配模式上分为离线模式和在线模式两种，离线模式是在已知任务信息和参与者信息进行分配，但是在响应时间有要求的情况下并不适用(例如外卖行业等)，并且在现实的场景中分配平台实现不可能了解到所有任务和工人的情况，所以离线模式只适合不需要高响应的任务，在线模式是指任务信息和参与者信息事前并不知道，只有当任务或参与者到达时才会知道其信息，例如Peng Chen[7]提出的MQA算法，通过分析地区任务出现情况来预测任务在某个时间段出现的概率，从而提高工人可以连续完成多个任务的概率以实现提高任务分配数量的提高.

随着人工智能的飞速发展，人们对于数据量的需求日益增长，传统的派专人采集数据的形式已经不能再满足人们的需求，空间众包利用MCS可以有效加快数据的采集速度和任务成本的控制，MCS技术是利用智能手机的传感仪器在手机空闲时采集四周的传感信息(如噪音强度，WIFI信号的强弱程度，交通拥堵情况等信息)，在成本上，传统方法是雇佣专业人士来采集信息，但是对于某些信息并不是一定要专业仪器才可以采集到，没有必要聘用专业人士利用MCS平台征集参与者利用参与者的智能手机同样可以采集到相同的数据，在OMG算法基于MCS平台通过反向竞拍的方式将任务分配出去，参与者通过公开报价的方式去获取任务，并且将分配过程分成了多个阶段，每个阶段录取的参与者的任务平均报价都会比之前阶段低，可以将任务成本有效降低，比使用传统方法雇佣专业人士去采集信息任务成本上要低很多，在时间上因为空间众包平台是利用网络来征集这段时间在任务地点附近并且有空完成任务的人，与传统方法去请人到工作地点采集要更加的快捷.

本课题组之前所提出的优化范围性空间众包分配算法(Optimizing Scope Spatial Crowdsourcing Tasks Allocation algorithm，OSSA)在空间任务中工作地点加入了范围属性，在任务分配之前将任务优化来消除任务冗余的问题，从而提高可分配任务数量.因为在感知信息采集时有时并不是采集一个地点的信息而实要采集一个范围的信息，但是在采集范围信息时，会出现任务范围的重叠导致任务冗余的现象，在人少任务多的情况下，过多的任务冗余会导致分配数量的下降.OSSA在识别任务关系和分配任务时，会将任务队列中所有任务进行比较，因此算法效率较低，本文所提出的OSSA改良算法的解决方法是将任务或工人的区域信息放入具有树形结构的任务树中，并且在存储时按照任务区域特性存储信息，从而在检索与到达任务或工人相关的任务信息或者工人信息时可以利用任务树实现快速检索.

本文首先介绍下OSSA算法，之后在OSSA算法的基础上利用二叉树将任务信息在空间上进行分类管理，当有新任务到达时，会利用之前存储范围信息的二叉树快速检索到与任务范围有冗余的任务，从而减小问题的规模并且加快识别任务关系的速度，进一步提高算法分配效率.本文组织结构如下：第二部分对研究背景与相关工作进行介绍；第三部介绍系统模型和问题定义；第四部分介绍利用二叉树将空间任务分类的优化算法并实例分析.第五部分，对设计的优化算法通过随机模拟工人和任务信息的数据，进行模拟仿真实验并给出实验分析结果，然后进行对比实验来证明优化算法的效果和正确性，第六部分为全文内容的总结以及对未来工作的展望.

2 相关工作

空间众包的优化问题，在近些年来被越来越多的研究者所关注，在优化方法中主要有三个目标，主要从分配数量，任务成本，任务质量三个方面去考虑，分配数量主要是考虑如何将最终分配的任务个数最大化，例如(GeoCrowd：Enabling Query Answering with SpatialCrowdsourcing)Leyla Kazemi[3]提出的LLEP方法，该方法主要是将工人出现的密度分等级分配任务时根据任务出现地区等级的高低去决定优先分配任务，来保证任务最大化分配数量.任务成本主要是优化最终分配的任务的平均成本即参与者的报酬，例如Frugal-OMZ[1]算法和OMG[8]算法都是在通过参考上一个阶段参与者产生价值与得到成本的比值作为阈值，将其作为下一个阶段选择参与者的指标，从而最大化降低任务完成成本，任务质量是指参与者完成所分配任务的质量，例如MELODY算法[9]采取分阶段的方式，将分配过程分成多个阶段，当工人完成任务后，会有一个质量的反馈，算法基于EM(Expectation-Maximization algorithm)算法根据前几次的所完成任务的质量来预估下次质量，根据工人质量的预测将任务分配给工人.

在上述的优化方法中，大多是从分配阶段对算法进行优化，任务优化是近年来一个新的优化方向，该方向是将任务之间的属性关联起来分析，任务不再是相互独立存在的，在文献[4]中总结了任务优化的三个主要优化方面，第一种任务的整合，是指将某些任务整合在一起交给参与者去完成[10-12]，例如Y.Liu[10]所提出的MT-MCMF算法通过分析参与者的行动轨迹将在将其轨迹范围内的任务整合交给参与者完成，实现最大化分配数量的目标.第二种是任务划分[13-16]它是将任务与任务之间属性的关联或者是任务与工人之间属性的关联将任务进行划分便于将来分配，减小分配的问题规模加快分配效率，例如文献[11]中认为工人在分配任务时并不是和所有任务都是有关系的，其利用树分解技术将有关系的工人或任务迅速找到，将那些不可能会出现在最优方法中的枝杈剪除，从而实现最大化任务数量的目标.文献[14]是利用分治的方法将仅和当前分配有关联的任务和参与者找到，进行局部的分配，从而提高分配效率，第三种任务分解[17，18]，在文献中为了完成复杂的问题将任务进行分解成一个个子任务，并将子任务分给参与者完成，最后将所有结果整合，从而实现提高任务的完成数量，文献[17]研究了任务分解后的不同完成任务的方式如顺序实现、并行实现和分治实现，文献[18]将任务分解应用到了图像采集中通过将任务分解让参与者从自己的角度去采集图像，所得到的结果是从不同角度拍摄的图像从而增强了任务的完成质量和所完成任务的容错率.

上述在任务划分的优化方法大多是针对任务是一个地点通过图的方式进行划分，而本文是将带有范围属性的空间众包任务利用树的技术将其分类，在优化任务时通过其关系节点在树中的位置推断其与其他任务的关系，从而迅速找到与之相关联的任务，减小寻找关联任务的问题规模，提高分配任务的效率.

3 系统模型的定义和目标系统模型

本系统基于OSSA算法的基础上加入了范围任务树，将会有一系列任务T{t1，t2…}和工人W{w1，w2…}到达系统中，任务内容是工人利用MCS技术通过智能手机中的传感器去采集目标区域中的相关感知信息(例如空气质量信息、交通信息、噪音信息等)，系统将会根据任务和工人信息给出分配结果，当任务t到达时，根据任务的范围信息将任务放入范围任务树中，并且利用其所在树节点的位置快速找到与之有关联的任务，然后根据关联任务与任务t在树中节点的相对位置来推断任务关系，在有工人w到达时，检索范围任务树找出符合工人接受范围的任务，如果发现符合条件的任务会立即分配，没有符合的任务将等待符合的任务出现，直到等待时间超过工人的离开时间，根据工人所完成的任务给出合理报酬，本系统由于是采用MCS技术收集感知数据，所以系统中出现的任务都是同质任务.

1)模型基本定义

模型定义基本参照OSSA算法，其中加入了关于范围任务二叉树的基本定义.

定义1.(任务时效性)每个任务ti都存在一个开始时间ai和一个结束时间di，ai是指任务的到达时间的时间点，di是指任务的离开时间的时间点，任务只有在ai和di的闭区间内才可以被分配.

定义2.(任务范围)每个任务ti都有一个任务范围，为了方便计算任务的范围，将所有任务的范围定义为一个矩形，由(ri，hi，wi)表示，ri是任务范围的左顶点，hi是任务范围的长度，wi是任务范围的宽度.

定义3.(工人时效性)每个工人wi都存在到达时间ai和结束时间di，ai是工人进入分配平台的时间点，di是工人离开分配平台的时间点，工人只有在ai和di闭区间内才可以接受任务.

定义4.(工人可接受任务范围)每个工人有一个可接受任务的范围，为了方便计算可接受的范围，将所有可接受范围定义为一个矩形，用(ri，hi，wi)表示，ri是可接受范围的左顶点，hi是可接受范围的长度，wi是可接受范围的宽度.

定义5.(工人报酬)每一个工人都有一个报价ci，系统会根据当时的分配情况给出工人报酬pi，为了保证工人权益即系统给出的报酬pi必须满足pi≥ci.

定义6.(任务编号)每一个任务都有自己任务编号，m为任务类型号，n为子任务编号，当任务t根据其任务范围分为了t1，t2时，其任务类型号为任务t的任务类型号，t1的子任务编号为1，t2的子任务编号为2，t的子任务编号为0.

定义7.(子任务标志位和子任务数量位)每一个根任务都有一个子任务标志位N和子任务数量位M，当有子任务分解出来时子任务的子任务编号是当前任务子任务标志位，并且更新根任务的子任务标志位加1，子任务数量位则是记录根任务中未完成子任务的个数.

定义8.(任务范围的起始点与结束点)任务的起始点指的是任务范围左上点即ri，而结束点为任务范围的右下点ei即(ri.x+wi，ri.y+hi ).

定义9.(范围任务树节点)范围任务树的节点由坐标值信息、任务编号、坐标点类型和右子树节点集合组成，其中的坐标值信息为坐标的x轴信息或y轴信息，任务编号即该节点所描述任务的任务编号，坐标点类型分为两类S，E用来记录该座标点是任务范围的起始点还是结束点，右子树节点集合记录了在右子树中只有起始坐标信息没有结束坐标信息任务的任务编号集合.

定义10.(任务分配数量)

(1)

(2)

定义11.(任务平均成本)：

(3)

2)模型假设

假设1.每一个工人最多只可以分配一个任务.

假设2.工人和任务的信息和到达的顺序事先是未知的，只有到达以后才可以获取任务和工人信息.

假设3.由于本文所讨论的范围任务都是基于MCS技术，所以工人在被分配任务时无需考虑工人能力问题，工人只要满足上节的三点要求就可以分配任务.

假设4.任务一旦被分配以后，工人一定可以完成任务，不存在中途放弃的情况.

假设5.工人不会拒绝系统分配给的任务，一旦分配任务会立即执行任务.

假设6.当工人到达时如果存在可分配的任务会立即分配可执行任务不会等待.

假设7.工人的数量远少于任务数量并且任务的分布是集中密集分布.

假设8.工人的报价是趋于稳定的，不会出现不真实的报价不会出现较大浮动的.

3)模型目标

利用范围任务树划分范围任务，在对范围任务检测时可以利用任务在范围任务树存放任务信息的过程获得的信息，快速鉴别那些可能会与任务有关联的任务，再通过任务树中节点的与关联任务的节点的相对位置，推断出任务的任务关系.然后利用OSSA的分配方法来解决任务冗余所带来的问题.

4 基于树形结构优化范围空间众包任务在线分配

由于本算法是基于OSSA算法改进而来，接下来会首先介绍OSSA算法的基本原理和流程，然后再介绍本算法对于OSSA算法的优化部分.

4.1 OSSA算法

OSSA算法主要是通过任务关系来解决节约范围性空间众包任务冗余问题，节约人力从而提高任务的可分配数量的方法.

4.1.1 任务范围冗余问题

任务范围冗余问题是指：多个工人在完成多个任务时会出现其所负责的部分与其他工人负责的部分之间出现重叠和部分重叠的问题.在空间任务分配时，由于任务的发布方往往不是同一个机构或客户，所以会导致任务与任务之间虽然是独立存在的，但是任务之间可能会存在空间依赖关系.在传统的分配算法中并没有考虑这个问题而是认为任务之间相互独立，因此分配任务时会出现任务空间之间的冗余.

接下来会给出两个案例来重点说明任务范围冗余的所带来的的人力浪费.

4.1.2 任务范围冗余的场景分析

在这个小节里会介绍两个案例来说明任务范围冗余出现的两种情况，分析范围冗余对任务分配情况的影响.

任务范围假设为矩形，范围信息由左上角坐标信息和矩形的长和宽组成.

任务t1，t2，t3是采集任务范围内的感知信息，工人会利用MCS技术利用自己的智能手机的传感器采集任务中的感知信息.

场景1.有两个工人w1和w2和两个任务t1和t2到达，两个工人的可接受范围为((0，0)，200，200)，任务t1的任务范围为((50，50)，100，100)，任务t2的任务范围为((100，100)，50，50)，工人w1和w2时间信息为(2，10)，w1的报价为1而w2的报价为5，任务t1的时间信息为(1，5)，任务t2的到达时间为(2，6)，详情如图1所示.

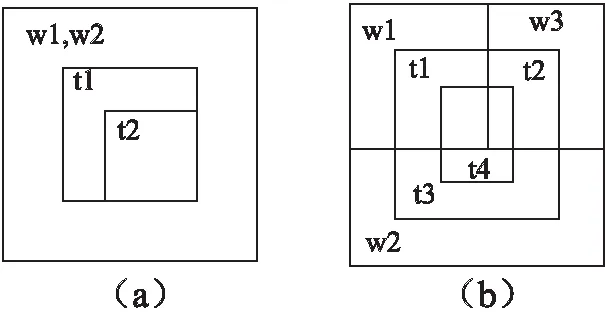
图1 场景1和场景2中工人和任务的范围信息

如图1(a)所示当t1和t2到达时，w1和w2都可以分配t1和t2任务，在传统分配算法中会直接分配任务给w1和w2，但是可以看出t1和t2之间的任务范围并不是完全独立的，而是存在交集部分的t2的任务面积是包含在t1中的，在之前的假设中工人可以完成任何任务，所以当在完成t1任务时，工人肯定会覆盖t2的任务范围，本来一个人就可以将t1和t2任务一起完成现在要两个人才可以完成，因为t1和t2的任务范围存在冗余部分(t2)，导致了分配时人力的浪费情况的出现.

场景2.有三个工人w1，w2和w3和4个任务t1，t2，t3和t4，w1的时间信息为(3，10)，w2的时间信息为(4，5)，w3的时间信息为(5，5)，t1的时间信息为(0，5)，t2的时间信息为(1，4)，t3的时间信息为(2，6)，t4的时间信息为(2，6)，任务和工人的范围信息见图1.

如图1(b)所示当任务到达时，t1，t2，t3分别在w1，w2和w3的到达范围内，所以w1，w2，w3可以分配t1，t2，t3，但是t4的任务范围却不被任何一个工人所覆盖，所以在传统的分配算法中，t4会被搁置直到有新的工人到达检测是否覆盖t4的任务范围，但是通过图2可以直观的看到，t4任务虽然不在任何一个工人的范围内但是t4的部分任务范围被其他三个任务的任务范围包含，即当完成其他3个任务时3个工人已经把t4任务的任务范围覆盖了，但是由于没有一个工人可以覆盖t4的整个范围导致t4任务无法被分配，在这种情况中，任务之间虽然在任务范围中没有出现直接包含的情况，但是任务与任务之间存在部分覆盖的情况，导致了任务范围冗余情况的出现，可以想象在任务数量巨大的情况下，少量的部分覆盖也会造成大面积的范围冗余情况的出现，从而出现分配时分配任务数量的下降.

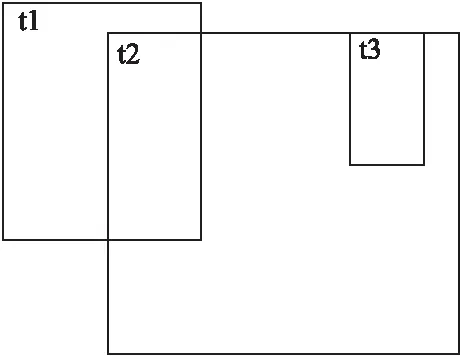
图2 实例分析场景

4.2 任务关系和节点关系

为了消除任务范围之间的关系，接下来会介绍三种任务之间的关系.

1)独立关系：存在两个范围任务t1和t2，其任务范围为S1和S2，若S1∩S2=Ø则t1和t2属于独立关系.

2)相交关系：存在两个范围任务t1和t2，其任务范围为S1和S2，若S1∩S2=S3≠Ø且S3≠S1和S3≠S1，则t1和t2属于相交关系.

3)包含关系：存在两个范围任务t1和t2，其任务范围为S1和S2，若S1∩S2=S2，则任务t1和t2属于包含关系.

4)被包含关系：存在两个范围任务t1和t2，其任务范围为S1和S2，若S1∩S2=S1，则任务t1和任务t2属于被包含关系.

如图1(a)所示，任务t1与t2在任务范围上存在交集部分t2，根据上文的任务关系定义，t1与t2的任务范围交集为t2，所以t1对于t2是包含关系，t2对于t1是被包含关系，如图1(b)所示，任务t1和t4也存在交集部分，但是交集部分不等于t1或t4的任务范围，所以t1和t4是相交关系，在图1(b)中任务t1和t2的任务范围不存在交集，所以t1和t2是独立关系.

从上述任务关系说明中可以看出在相交关系和包含与被包含关系中存在任务范围冗余的问题，所以OSSA算法的目标是通过将任务整合和分解的手段，将每一个任务和除它外的所有任务的任务关系转化为独立关系从而消除任务范围冗余的问题.

4.3 OSSA算法设计

为了跟好的理解算法，首先会在表1中介绍算法中会出现的变量以及变量的含义：

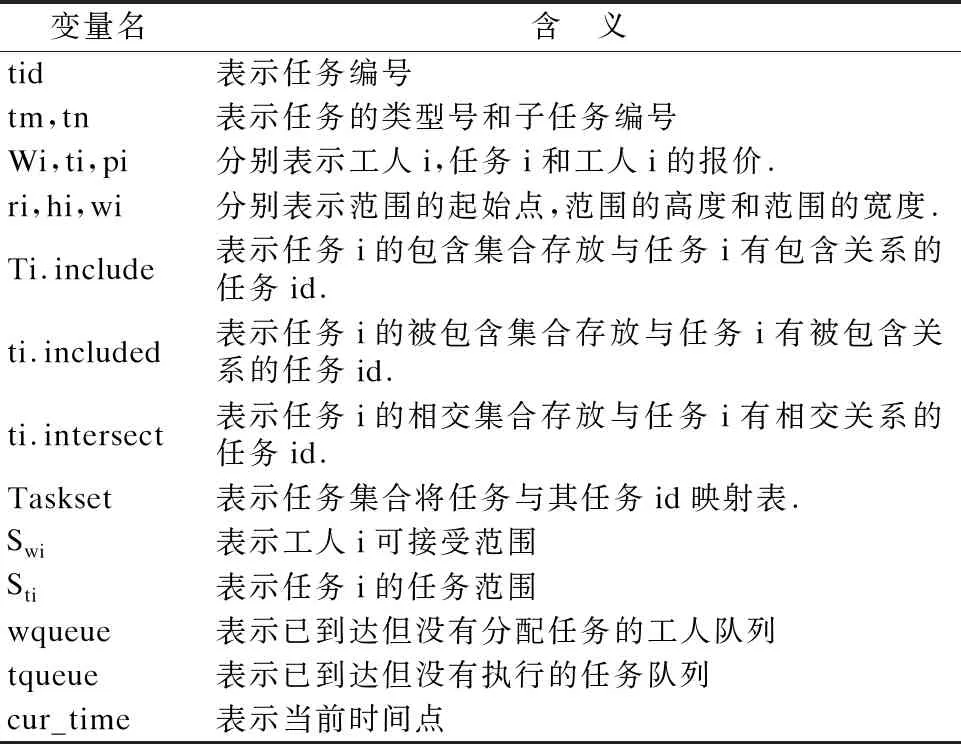
变量名含 义tid表示任务编号tm,tn表示任务的类型号和子任务编号Wi,ti,pi分别表示工人i,任务i和工人i的报价.ri,hi,wi 分别表示范围的起始点,范围的高度和范围的宽度.Ti.include表示任务i的包含集合存放与任务i有包含关系的任务id.ti.included表示任务i的被包含集合存放与任务i有被包含关系的任务id.ti.intersect表示任务i的相交集合存放与任务i有相交关系的任务id.Taskset表示任务集合将任务与其任务id映射表.Swi表示工人i可接受范围Sti表示任务i的任务范围wqueue表示已到达但没有分配任务的工人队列tqueue表示已到达但没有执行的任务队列cur_time表示当前时间点

OSSA算法具体内容：

算法1.OSSA

n=0

ui arrive

Su=compterarea(ui)

if T !=cur_time：

detect_time(cur_time)

sign=False

if(type(ui)==Worker)

for t in tqueue：

if St∩Su=Stand count(t.include)>=count(task.include)：

if count(t.include)==count(task.include)：

if count(t.intersect)> count(task.intersect)：continue

pi=area_salary(t.id，u)

task=t

sign=True

if not sign：

wqueue.add(u)

else：

u.id=n

n+=1

Taskset[id]=u

task_relation(u.id)

if u.included !=Ø

for w in wqueue：

if Sw∩Su=Suand minprice > cw：

selectedworker=w

pw=area_salary(u)

minprice=cw

sign=True

if not sign：

tqueue.add(u.id)

else：

delete_relation(u.id)

wqueue.remove(selectedworker)

Taskset.pop(u)

在OSSA算法中，如果是任务到达时会首先检测该任务和任务队列中的任务之间的关系，如果该任务与某一任务存在被包含关系(即该任务的任务范围与其他任务完全重叠)，则不会将任务放入任务队列中，若没有存在任务与其有被包含关系则将其放入任务队列中，在识别任务关系时，会将存在关系的任务根据关系类型分别储存在不同关系队列中，方便分配任务时方便整合任务内容，当有任务离开任务范围分解或被分配时会根据其关系队列重新更新与之有范围关联的任务的关系队列，当工人到达时会根据工人的工作范围从任务队列中搜索可完成的任务，然后将任务按照所包含的任务个数将其重新摆列，挑选出包含任务最多的任务交给工人完成，工人所获得的报酬会根据任务范围的大小和其所包含任务个数和其占包含任务的任务范围的比例综合计算，通过OSSA算法可以将范围任务有效优化，使得分配给工人的任务是在当时阶段完全独立的任务，有效减轻了任务冗余所带来的问题.

在OSSA算法中，在对任务的任务关系初始判断时，会将任务队列中每一个任务都会进行判断然后得出该任务与其他任务之间的关系，当任务数量越来越多时，关系判断时间会线性增长，会极大降低算法的效率，接下来会介绍本算法如何利用空间任务树将任务进行划分，从而有效的找出可能存在非独立关系的任务.

4.4 改进算法

改进算法主要是在任务关系判断环节对OSSA算法进行修改，使其可以快速将可能存在关系的任务从任务队列中划分并识别出任务关系.

下面会列出改进算法中会出现的变量和变量的意义

变量名含 义id分别表示任务编号tm,tn表示任务编号中的任务类型号和子任务编号XTree表示任务在X轴投影的任务树YTree表示任务在Y轴投影的任务树node表示树的节点node.type表示树中存放坐标的含义,S代表该节点表示任务范围的初始点,E代表该节点表示任务范围的结束点node.value表示节点存放的坐标值node.leftid存放了该节点右子树中只有任务范围的初始点却没有终结点所代表任务的任务编号node.kind表示节点种类,T代表存放的是任务信息,W代表存放的是工人信息node.id表示树所代表任务或工人的编号Tnode.left表示节点的左节点Tnode.right表示节点的右节点XTree.firstYTree.first表示X轴投影树的根节点表示Y轴投影树的根节点

改进算法具体内容：

算法2.Improved OSSA

n=0

ui arrive

detect_time(cur_time)

sign = False

if(type(ui)==Worker)

updateTree(ui)

if ui.include==null

wqueue.add(ui)

else

queue=ui.include

task=null

max=0

for t in queue

if t.included !=null

continue

if count(t.include)>max

max=count(t.include)

task=t

if task

pi=area_salary(task.tid，u)

deletenode(task)

deletenode(ui)

else

update(ui)

for node in ui.included

if node.kind==w&&minprice>=c

selectedworker=workerset.get(node.id)

minprice=c

sign=true

if sign

pi=area_salary(ui，selectworker)

wqueue.remove(selectworker)

deletenode(ui)

deleternode(selectworker)

在改进算法中，在分配方面沿用了OSSA的机制，但是在任务关系识别方面，使用了范围任务树将范围信息存储到树中，当工人或任务到达时会首先将其范围信息放入到树中，根据其所属节点在范围关系树的相对位置，判别出任务关系，在每次分配完毕后会将已分配的节点在关系树中进行更新，将已分配的节点从树中剪除.

算法3.updateTree

relationX=updateX(ui)

relationY=updateY(ui)

if type(ui)=W

for id，kind in relationX

if kind !=1

continue

if relationY.get(id)!=null and realtionY[id]==1

if id in taskset

ui.include.add(id)

else

for id，kind in relationX

if relationY.get(id)==null

continue

if kind==0 and id in taskset

ui.intersct.add(id)

taskset.get(id).intersect.add(id)

if kind==1

if relationY[id]==1

ui.included.add(id)

if id in taskset.key

taskset.get(id).include(ui.id)

else

workerset.get(id).include(ui.id)

else

if id in taskset

ui.intersect.add(id)

taskset.get(id).intersect.add(ui.id)

if kind==2

if relationY[id]==2

if id in taskset.key

ui.include.add(id)

taskset.get(id).included(id)

else

if id in taskset

ui.intersect.add(id)

在改良算法中，工人和任务之间也可以用任务范围确定关系，但是工人与任务之间只有包含关系，因为只有当工人的工作范围完全覆盖了任务范围才可以完成，所以工人与任务之间的相交关系和被包含关系没有任何意义.首先算法会将任务/工人的信息分别放入代表X投影和Y投影的范围任务树中，然后根据从返回的任务节点在两个树中的关系，可以推断出任务与现有任务之间的关系或工人与任务之间的关系，节点关系和任务关系的映射见表1.然后将识别好的关系放入关系队列中.

表1 节点关系与任务关系映射表

算法4.UpdateX/uUpdateY

snode←(ui.id，S，ui.x，null，ui.type )

enode←(ui.id，S，ui.x+wi，null，ui.type)

set1=updateNode(ui)

set2=updateNode(ui)

detect_relative(set1，set2-set1)

在UpdateX或UpadteY函数中，会根据任务或工人信息计算其范围的起始点和结束点在x轴和y轴的坐标，然后初始化树节点，节点编号为任务或工人编号，set1和set2为比放入小于起始点和结束点的节点id，然后通过这些信息得出任务节点在树中的节点关系.

算法5.UpdateNode

node put in Tree

root=Tree.first

tasked=[]

prenode=null

while root

prenode=root

if root.value<=node.value

tasked.add(root.id)

for id in root.leftid

tasked.add(id)

root=root.right

if root.value>node.value

root=root.left

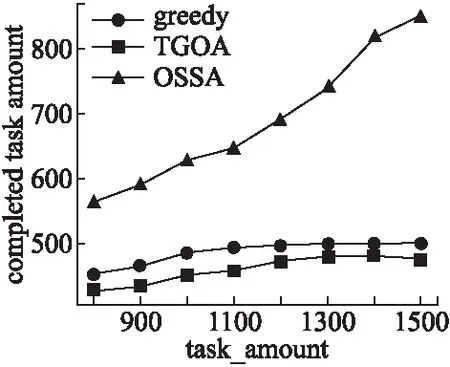
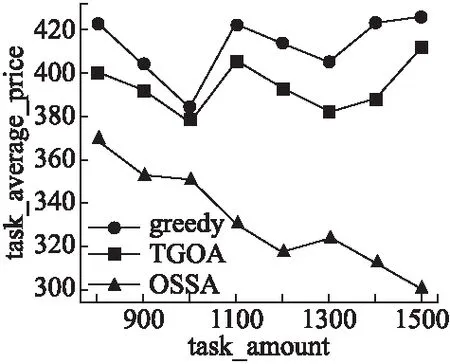
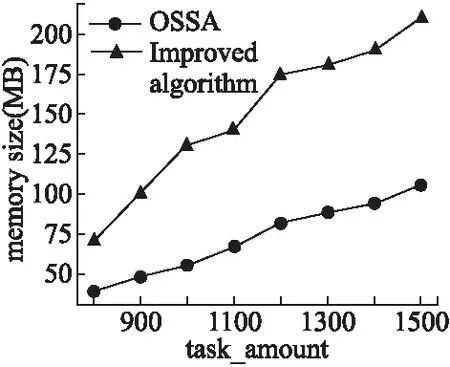
if prenode.value

for id in prenode.leftid

if taskid.exist(id)

tasked.remove(id)

else

tasked.append(id)

prenode.right=node

else

prenode.left=node

if node.type==E

taskset.remove(node.id)

return tasked

在updateNode函数中，会根据节点中的值放入相应位置，首先插入节点会和树的头节点比较如果比插入节点的值要小，下次会和该节点的左节点比较，否则下一次和该节点的右节点比较，直到比较的节点为空为止，则将插入节点信息覆盖该空节点，另外在整个插入过程中遇到比自己值小的节点会将其id记录下来并且将其右子树中的节点放入，每一次遇到比自己大的节点，该节点会将其id记录在自己leftid集合中，函数最后将记录的id集合返回.

算法6.detect_relative(set1，set2-)

nodeRelationship={}

occur1，occur2={}，{}

for id in set1

if occur1.get(id)==null

occur1[id]=0

occur1[id]+=1

for id in set2

if occur2.get(id )==null

occur2[id]=0

occur2[id]+=1

for key，count in occur1

if count==2

continue

if occur2.get(key)!=null

occur2[id]=0

nodeRelationship=0

else

nodeRelationship=1

for key，count in occur2

if count==0

continue

if count==1

nodeRelationship[id]=0

else

nodeRelationship[id]=2

return nodeRelationship

在该函数的作用是将任务范围的起始点和结束点在树中返回的id集合进行分析，得出其与其他任务在x轴或y轴上的关系，set1代表的是起始点返回的id集合，set2代表的是结束点返回的id集合与set1的差集(即将出现在set1中的元素删除)，首先会分别记录在两个集合中id出现的次数，如果在set1中出现只有一次而在set2中出现过则为相交关系用0代表，反之若在set2中没有出现则为被包含关系用1代表，然后检查在set2中节点出现次数如果只出现一次则为相交关系如果出现过两次则为被包含关系用2代表，最后返回记录节点关系的字典.

算法7.deletenode

if type(ui)==w

for id in ui.include

taskset.get(id).included.remove(id)

else

for id in ui.include

taskset.get(id).included.remove(ui.id)

deletenode(ui)

for id in ui.included

if id in taskset

taskset.get(id).include.remove(id)

for id in ui.intersect

deleteAllraltionship(taskset.get(id))

nodes=descompose(ui，taskset.get(id))

deleteFromTree(taskset.get(id))

for n in nodes

update(n)

snode=taskset.get(ui.id).snodeX

enode=taskset.get(ui.id).enodeX

deletenodefromTree(snode)

deleternodefromTree(enode)

snode=taskset.get(ui.id).snodeY

enode=taskset.get(ui.id).enodeY

deletenodefromTree(snode)

deleternodefromTree(enode)

该函数的目的是将已分配的任务和工人删除其在算法中的所有信息，首先会判断是工人还是任务，如果删除的工人，则将其所包含任务的被包含队列里把其id删除，如果删除的任务，首先将其id从其他任务的包含队列中删除，然后遍历其相交队列，将与其相交的任务去除相交部分，然后根据具体的相交情况，将剩余任务区域分解成若干个新的任务放入任务树中，将被分解的任务从树中删除，最后将被其所包含的任务从树中删除，最后将该任务在任务树中删除.

算法8.deletenodefromTree

delnode=nodes.get(id)

leftnodes，newleftnodess=delnode.leftid，null

leftnode=delnode.left

While delnode.right and delnode.right.right

rnode=delnode.right

newleftnodes=rnode.leftid

rnode.leftid=leftnodes

newleftnode=rnode.left

rnode.left=leftnode

leftnode=newleftnode

leftnodes=newleftnodes

delnode=delnode.right

if delnode.right.left

swap(delnode.right.left，delnode)

deletenodefromTree(delnode)

else

delnode.right.leftid=leftnodes

delnode.left=leftnode

该函数用来将任务节点从任务树中删除，首先会检查该节点的右节点是否存在如果不存在就寻找其左节点存在则由其左节点来代替其位置如果不存在则返回，如果右节点存在则检查其节点的右节点是否存在，如果存在则将右节点信息覆盖要删除的节点将将要删除节点的leftid赋给右节点，然后利用同样的方法将原来右节点从树中删除一直递归直到不符合条件为止，若不存在就判断该节点的左节点是否存在如果存在则将左节点来覆盖删除节点信息，然后将原来的左节点放入函数中递归，如果左节点不存在则将右节点替换要删除的节点.

4.5 实例分析

首先用通常的分配算法，认为任务之间是相互独立存在的，对任务进行分配，然后会使用改良算法对任务进行分配，由于改良算法是对OSSA算法中任务关系识别环节的改进，而在分配任务和工人报酬方面依然是沿用OSSA算法的方法，所以在实例分析中会在场景里放入先后出现的任务，然后利用改进算法来识别任务之间的关系，来证明改良算法对于任务关系识别的可行性.

实例说明假设有3个基于MCS完成的任务来自不同的机构是采集三个不同区域的信息来做相关工作，为了方便计算将任务范围简单定义成一个矩形区域，所有任务的发生区域简单定义为一个XY轴坐标组成的区域，任务范围信息由矩形的左上角坐标和矩形的长宽构成，任务信息由任务范围信息和任务的报价组成，工人之间的采集工具(智能手机)可采集信息完全相同.

在图2中有t1，t2，t3三个任务，它们是依次出现的，任务信息如下：t1(5，3，4，5，4)、t2(8，4，15，12，5)、t3(10，4，12，，6，6)，任务出现顺序是t2、t1、t3，t1和t3是采集区域的噪音信息而t2是采集WIFI信息强弱信息，在贪心算法和TGOA算法中认为三个任务之间是独立的，会将三个任务分配给三个不同的人完成，但是可以从图2看出t2和t3之间是存在范围重叠的(即t2和t3之间存在任务冗余问题)，而t2和t3的任务内容虽然不同但是在任务是基于MCS技术，是利用手机中的传感器来收集区域的信息，所以在分配给t2任务的功能的工人其实在完成过程中也会经过t3的任务区域，由于在前提假设中工人之间的手机可采集的信息是相同的，则完成t2任务的工人其实完全有能力完成t3任务，由于任务冗余明明只有2个人完成的任务现在需要3个人完成.

接下来会利用改良算法辨识任务之间的关系，证明改良算法对于任务识别结果是和使用OSSA算法一致的，另外通过例子来进一步理解改良算法的基本流程.

一开始t2到达时，将其任务区域信息放入空间树中，放入后的具体结果见图3(a)，由于是第一个到达任务所以没有任何任务关系产生.

图3 各任务到达后树的情况

t1到达后将空间树的信息放入其中，放入后详细情况见图3(b)，在存放t1的初始点x坐标时，首先和t2的初始节点比较，发现小于节点的值所以将其放入头节点的左子树，并且头节点会记录放入其左子树的任务id(即t2的id)，由于没有值小于t1初始节点的坐标值所以返回集合为空，而放入t1的结束点的坐标时，由于t2的初始节点的坐标小于其只，所以会返回一个t2的id，所以t1和t2在x轴投影上的关系是相交关系.同理在放入t1的初始点的y坐标时，由于没有比其小的节点返回为空，而放入t1的结束点的坐标时会发现只有t2的初始节点的值比起小，所以会返回一个t2的id，所以t1和t2在y轴的投影关系是相交.通过综合x，y轴的投影关系得出t1和t2是相交关系.

t3到达后将其信息放入树中，放入后的详细情况见图3(c)，在存放t3初始点的x坐标时，由于t1的两个节点的x坐标都小于它，而t2只有初始节点小于它，所以返回的是两个t1的id和一个t2的id，同理在放入t3结束点的x坐标时会返回相同的结果在任务识别中由于t1的id出现了两次在set1中，所以t3和t1在x轴投影上没有关系，而set2是将结束点返回结合中删除set1的元素，由于set1和set2相同所以set2为空，根据算法可以的出t3和t2是包含与被包含关系，当放入t3初始点的有坐标时，会发现t2的初始节点坐标和其相同而t1的初始节点坐标小于它所以会返回一个t1的id和一个t2的id，同理放入t3结束点y坐标时会返回相同结果，由于两个点返回的结果一致所以set2为空，根据算法得出t3与t1和t2在y轴投影是包含与被包含关系，由于t1和t3在x轴投影没有关系所以t1和t3是独立关系，而t2和t3在x，y轴都是包含关系所以t2和t3是包含关系.

从这个例子中可以了解改良算法对于任务关系识别上得出的结果与使用OSSA算法得出的结果是相同，在改良算法中，将三个任务放入了两个任务树中，在处理工程中发现了t2和t3在两个树中的坐标信息同时出现包含关系，则t2与t3的关系时包含关系，则会将t2和t3合成一个任务，从而避免了任务冗余问题带来的人力浪费的问题，另外改良算法在确认任务关系时，并没有像OSSA算法中遍历任务队列中的任务确认任务之间的关系，而是利用任务树坐标的情况迅速找到与其任务范围相关的任务确认其任务关系.

5 实验分析

本节首先会将OSSA算法与TGOA算法和贪心算法在可分配任务数量和任务成本上进行对比，证明改良算法所改良的OSSA算法的正确性和可行性.然后将改良算法与OSSA算法处理时间进行对比，比较两种算法的执行速度，证明改良算法对执行效率的改良.实验设备介绍：实验将在win10系统下运行，实验的程序是由python语言编写，编译平台为pycharm，电脑cpu为 i7-6700，内存为16g.

实验数据：整个场景为300*300的平面假设有工人500人其报价在[1，10]之间随机产生，工人出现地点在全图范围内随机产生，工人可接受范围在[1，100]*[1，100]区间随机产生，任务个数在800-1500之间每隔100取一次，任务地点随机产生，任务范围在[1-50]*[1-50]区间随机产生.

实验1.将固定工作人员数量并逐渐增加了任务数量，以验证OSSA使用任务优化后的任务数量是否大于没有任务优化的算法数量.由于该算法针对的是任务较少的工作人员，因此任务数量将从超过工作人员数量开始.因此，实验设计人员的数量逐渐从800增加到观察完成任务.在本实验中，OSSA完成的任务数和没有任务优化的分配算法仅限于在给定数量的任务下每个工作人员的一个任务.从图4中可以看出，OSSA算法与其他两种算法随着任务数量的增加可分配任务数量之间的差距会逐渐增大，由于任务冗余会造成人力的浪费，在工人只能分配一次的情况下，由于对任务本身范围的优化使得最大可分配数量得到提高.

图4 任务完成数对比

实验2.当固定工人数量逐渐增加时，验证OSSA算法的任务平均价格不会超过未使用任务优化算法的任务平均价格.从图5可以看出，任务的平均价格随着任务数量的增加而逐渐减少.由于数据的随机性，其他两种算法上下波动，但从未低于OSSA算法的平均价格.当任务范围内的冲突数量不断增加时，包含任务和交叉任务的改良任务的平均价格低于当时的单个任务价格.因此，当冲突次数逐渐增加时，已完成任务的平均价格将逐渐下降.

图5 任务平均价格对比

通过上面两组实验可以证明OSSA算法在解决具有范围性任务分配问题上的可行性和正确性.

实验3.将工人个数固定逐渐增加任务个数，对比OSSA与改良算法之间在运行效率，从图6中可以看出当OSSA算法与改良算法随着任务个数的增多，改良算法与OSSA之间的运行时间逐渐增大，这是由于当任务个数增多时，OSSA算法在工人到达或任务到达检查关系时，是将任务队列或工人队列中的信息拿出来一个个与到达工人或任务的区域信息对比，而在改良算法中当有工人或者任务到达时会将任务区域信息在任务树中进行检索查看是否有相关的信息，而不是与现有数据一个个对比获得，所以当任务数量增大时改良算法与OSSA算法运行时间的差距会逐渐增大.

图6 OSSA与改良算法运行时间对比图

改良算法主要是改动了OSSA算法中任务关系识别过程，在时间上在OSSA算法中会将任务放入任务队列中将任务与任务队列中的其他任务放入任务信息中，在判断任务之间的关系时，会遍历整个任务队列得出任务之间的关系所以时间复杂度是O(m*n)，n为现有任务队列中的任务个数，m为与任务存在任务范围冗余任务的个数，而改良算法中会额外建立一个空间任务树来存放任务范围信息，利用树形结构可以迅速索引到与自己任务范围相关的任务，其时间复杂度为O(mlogn)，改良算法通过增加空间任务树在现有任务的任务范围中建立索引，加快找到新到达任务与之在任务范围有关系的任务判断任务关系，因此具有更高的执行效率.

6 总结与展望

在改良算法中针对OSSA算法在搜索任务关系过程进行优化，使得识别任务关系不用和现有任务一一对比，而是将任务信息放入空间任务树中，检查代表任务区域的两个节点与其他节点之间的关系来推断出任务关系，从而加快了任务关系识别速度，通过对比实验可以证明改良算法的识别速度在任务多的情况下由于原有算法，而且因为其他环节是与OSSA算法一致的，所以最后的分配结果是不会改变.

改良算法由于是利用树形结果进行优化搜索，在一些极端情况下会出现线性搜索的结果，对于这种情况可能会在未来通过某种机制对这种情况进行改进.

在算法中，假设了任务是同质任务(即工人有能力完成所有类型的任务)，但是在现实中由于人们智能手机的不同所能采集的感知信息是不同的，为了更加符合现实需求，接下来会主要去研究工人所能完成任务有差异的情况下如何去避免任务范围冗余的问题.