浅谈定积分的几何应用

左 玲

0 引言

大学生活是丰富美好的，多样化的学科知识对学生今后的发展起着至关重要的作用。高等数学是大一新生普遍会学习的一门数学基础课。其对接下来的数学类课程的开展有着重要的基础作用。同时，学好这门课程也有利于学生对其专业课程的理解与掌握[2]。然而，较强的逻辑思考和较为单一的书面讨论形式使大部分的学生对高等数学产生了一种比较刻板的印象，认为其枯燥晦涩，难以掌握，常常令大部分同学感到望而生畏。怎样开展这门数学基础课程的教学对大学学习尤为重要，是大学数学学习中值得探讨的一个问题。如何在高等数学的课堂教学中恰当地做到理论联系实际，进而提高同学们的求知欲与学习能力呢？

在高等数学的学习中，研究的基本问题是函数的性质与形态。高等数学的上册主要针对的是一元函数，下学期是对上册内容的推广和深入拓展。其中对函数的分析主要体现在函数的微分学与积分学两个方面。因此，本文结合一元函数的积分问题和大家探讨高等数学的教与学。定积分是函数积分问题的重要开端，如何生动而丰富地理解定积分，同时运用定积分求解实际问题，这是本文将逐一分析的内容。具体地，通过对定积分的几何应用这一节内容的教学设计来简单地探讨这个问题。在同济大学第7 版的高等数学中[1]，我们在第六章第二节中讨论了定积分的几何应用。具体地，利用定积分计算了平面图形的面积、旋转体的体积、平行截面面积已知的立体体积、平面曲线的弧长。本文针对定积分求解平行截面面积已知的立体体积这一问题来探讨本节的教与学。

1 结合曲边梯形问题提出元素法

在前面的课程中我们介绍了定积分的概念。结合具体的实际问题引导学生思考定积分概念的由来和在实际应用中的背景。这与本节讨论的定积分求解平行截面面积已知的立体体积有着相似的分析方式。因此，首先引导学生回顾这一部分的内容，感受知识点相互之间的紧密关联。考虑闭区间上的连续函数与坐标轴围成的曲边梯形的面积。通过分割、近似替代、求和与取极限四个步骤来处理不规则的曲边梯形的面积问题。经过任意分割之后的每一份小的曲边梯形进行近似，用矩形替代，无限细分，并且运用极限求解这个无限变化过程中的精确解。即曲边梯形的面积。从中体会化整为零和以直代曲的思想，用严格的数学形式刻画定积分求解面积的原理。几何的直观表达可以有效地提高学生对代数表达式的兴趣与理解程度。

通过对曲边梯形面积的分析抽离出一种一元函数的乘积的和式的极限，将其定义为定积分。定积分中蕴含着怎样的数学思想呢？能否将其用数学的语言来表达？可否运用这种数学思想求解其他的问题呢？这就需要依附曲边梯形的面积问题推导出定积分的元素法，分析运用元素法时目标对象需要满足的条件，归纳元素法解决问题时的步骤。强调定积分与元素法相辅相成的关系。同时这也是本节课探讨的主题：定积分的元素法以及如何运用元素法求解平行截面面积已知的立体体积。定积分的元素法是定积分概念的简化版本，是抽象出来得更为简洁的教学形式。换个角度来思考，定积分的元素法是对其进一步的推广。定积分的元素法主要包含三个步骤：

（1）合理地选择选择积分变量。

（2）求出部分量ΔU 的近似值dU 的表达式，这也是最关键的一步。

（3）对dU 求积分得到U。结合曲边梯形问题，可以得到部分量 ΔA 的近似：dA=（fx）dx，则面积为

2 引用经典案例，提高学生学习的兴趣

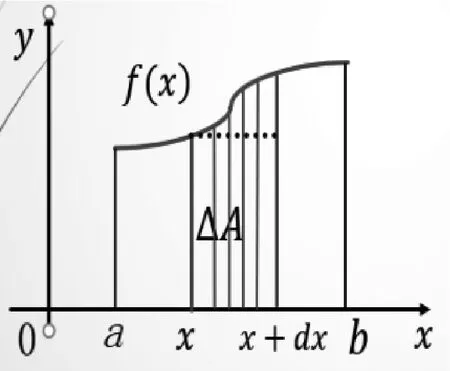
图1

然后，结合实际问题背景吸引学生学习这一课题的兴趣。南朝数学家祖暅在其经典的数学著作《缀术》中有云：“缘幂势既同，则积不容异”。意思是两个不同的立体，如果立体的高和任意截面面积相等，则这个立体的体积相同，为什么呢？通过将理论联系实际，一方面提高学生参与讨论的积极性，另一方面引导学生感受中国古代博大的数学文化和深邃的思想。引导学生观察这两个立体的不同点和共同之处，启发学生思考怎样将其与定积分的元素法结合起来。

3 运用元素法分析平行截面面积已知的立体体积

接下来，介绍平行截面面积已知的立体，即两个立体的任意垂直轴的平行截面面积相同。这一部分的重点是分析如何运用元素法求解这一几何问题。

【重点：元素法推导平行截面已知的立体体积的计算公式】本章主题是探讨定积分元素法的应用问题。除了求解不规则平面图形的面积，还能运用定积分解决哪些几何问题？这也是对定积分应用在其他领域的重要尝试[3]。引导学生探讨如何运用元素法将平行截面已知的立体体积转化为定积分的计算。在这一过程中注意强调对元素法原理的理解。

【解决方法】在教学过程中，拟采用逐层深入的方式探讨元素法的原理及其在求解平行截面已知的立体体积中的应用。结合图形启发学生思考元素法适用的问题类型，需要满足哪些条件的要求。在计算平面面积的几何问题中，归纳操作元素法的基本步骤。然后提出问题：平行截面面积已知的立体是否具备使用元素法的条件呢？怎样合理地选择积分变量？采用对比的方式使学生感受不同的选择对积分产生的影响。接下来，当确定积分变量后，如何根据几何体的特点求解平行截面面积函数？在这个过程中结合板书推导的方式强调对面积函数的分析。最后，根据截面面积函数与定积分的计算，解决立体体积问题。

图2

【难点：平行截面已知的立体体积的计算】运用定积分求解平行截面已知的立体体积时需要计算出立体平行截面的面积函数。而空间几何体的抽象性使得学生较难直观地感受到立体的几何特性。因此，如何提高学生的空间几何的解析能力是一个有挑战性的问题。

【解决方法】本节段采用特殊到一般的方式展开对难点的分析：首先，列举一些大家较为熟悉的几何体，通过板书详细解答例题的演练过程，积累关于常见几何体的处理方法和技巧。然后，逐渐过渡和推广到较复杂的几何类型。通过多媒体辅助的形式，增强学生对几何体的空间感受力。在这个过程中培养学生的空间几何的解析能力。最后，总结求解立体截面过程中的一般步骤。

图3

主要分为三步：

（1）定变量：x[a，b]。

（2）找微元：dV=A（x）dx。

因此，对体积元素积分，得到平行截面面积已知的立体体积的计算公式最后，回到刚才列举的引例中，用元素法得到的平行截面已知的立体体积公式解释“祖暅原理”。

4 将理论联系实际案例加深学生对重难知识点的理解

结合定积分的概念启发学生思考元素法的归纳过程。引导学生学会结合定积分的定义与曲边梯形的面积来提炼出元素法。了解元素法适用的问题类型，掌握其使用时的具体步骤。目标对象可以表示为某一元素的求和，并且元素为一元函数与长度微元的乘积形式。探索能否运用这种比较抽象的数学方法来解决其他几何问题。例如：怎样运用定积分的元素法求解平行截面面积已知的立体体积？教会学生辨识平行截面面积已知的立体。能够判断此类几何问题是否满足元素法的适用条件。再次回到引例中，当两个立体高相等，且平行截面面积相同时，根据定积分求解平行截面面积已知的立体体积公式知道，这两个立体的体积相同。

5 总结和拓展

本节探讨了定积分的元素法在几何问题中的应用。采用了问题引导式的教学方法，结合平行截面面积已知的立体体积问题引导大家思考定积分的元素法的使用。启发学生理解定积分的化整为零与以直代曲的基本思想[4]。同时，通过“祖暅原理”感受古今中外数学家们的智慧结晶，体会数学学科的实用性。培养学生学习数学知识的热忱。培养学生的数学素养，体会数学的概念与方法是在对实际问题的分析过程中抽离出来的，反过来，这些结论又在实践中逐步地发展、丰富与完善。进一步地，引导大家思考，除了几何问题还有哪些实际问题可以通过定积分的元素法来求解，从而为下一节的探讨做出铺垫。